二阶非齐次偏微分方程特解的教学探究

桑彦彬 史娜 张健

1.中北大学数学学院 山西太原 030051；2.中国石油大学理学院 山东青岛 266580

1 概述

近年来，对于二阶非齐次线性常微分方程特解计算的教学探讨受到了广泛的关注。文献[1]对经典的待定系数法求特解的方法进行了简化。进一步，文献[2]将矩阵方法和待定系数法进行了结合，建立了二阶非齐次常微分方程特解的公式解。文献[3]提出了伴随方程的定义，将非齐次项分为三种不同的类型，分别给出了特解的求法。与上述文献不同，文献[4]通过常系数齐次方程的线性无关的特解，建立了对应的非齐次问题的特解，推广了待定系数法和常数变易法。最近，文献[5]改进了教材[6]中两种类型的特解计算和文献[7]的特定取值法。另一方面，微分算子法和微分算子级数法在非齐次常微分方程和偏微分方程特解的计算中也得到了一定的应用。文献[8]通过引入微分算子，讨论了线性常微分方程通解和特解的求法。进一步，文献[9]研究了微分算子级数法在波动方程初值问题中的应用。文献[10]介绍了几类非齐次常微分方程特解的微分算子级数法，改进了微分算子法。数学物理方程教材[11]系统地论述了微分算子法在求解热传导方程和波动方程通解中的应用。

非齐次偏微分方程特解的求法在数学物理方程的教学实践中是无法回避的，然而其计算并无通法，只能依据非齐次项的特征，针对不同的类型进行求解。本文研究了直接积分法和微分算子法在几类非齐次偏微分方程中特解的具体应用。设二阶常系数线性非齐次偏微分方程的一般形式为：

Auxx+Buxy+Cuyy+Dux+Euy+Fu=f

2 直接积分法

(1)若F=0，f=C。

此种情形，可令uxx=uxy=uyy=0，进一步，ux=C，或ux=C。由于此时取一阶偏导数为常数，二阶偏导数必为零，直接积分即可得到方程的特解，进行这样的假设是合理的。

例1 求4uxx+5uxy+uyy+ux+uy=6的特解。

解：令uxx=uxy=uyy=0，进一步取

uy=0，或ux=0，

则ux=6，或uy=6。

故该方程的特解可取u*=6x，或u*=6y。

(2)若E=F=0，C≠0，f=C1y+C2。

由于此时非齐次项只含有y，不含x，f关于x的一阶和二阶偏导数均为零，则Cuyy=C1y+C2，对y直接积分可得其特解。

例2 求uxx+10uxy+9uyy+7ux=3y+2的特解。

解：令uxx=uxy=ux=0，则9uyy=3y+2。

同理，若D=F=0，A≠0，f=C1x+C2。此时非齐次项只含有x，不含y，可令uxy=uyy=uy=0，则Auxx=C1x+C2，也可直接积分可得其特解。

(3)A，B，C，D，E，F均不为零，且f=C1x+C2，或f=C1y+C2。

若f=C1x+C2，由于f只含有x，不含y，可设uxx=uxy=uyy=uy=0，此时退化为Dux+Fu=f，可借助于一阶线性非齐次常微分方程通解公式获得其特解；同理，若f=C1y+C2，由于f只含有y，可设uxx=uxy=uyy=ux=0，此时退化为Euy+Fu=f，亦可得出其特解。

例3 求3uxx+7uxy+2uyy+ux-3uy-2u=2x+1的特解。

解：令uxx=uxy=uyy=uy=0，则所求方程转化为ux-2u=2x+1。将此时u=u(x，y)看作只与x有关，即可得到以下特解：

与文[3-5]相比，此处的直接积分法简便易用，且对于非齐次项为仅含有单变元的线性函数均是适用的。进一步，该方法也可应用于更一般的初边值问题。

3 微分算子法

若A，B，C，D，E，F均不为零，且f=C1x+C2y。

此时，f含有x与y，直接积分法和采用一阶线性非齐次方程的特解求法均失效，而微分算子的引入提供了适当的框架。同时，可利用幂级数的展开式直接参与运算。

例4 求3uxx+7uxy+2uyy+ux-3ux-2u=2x+3y的特解。

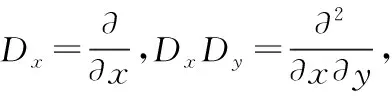
即:

(Dx+2Dy+1)(3Dx+2Dy-2)u=2x+3y.

设:

解之:

=2x+3y-Dξ(2x+3y)

=2x+3y-(2xξ+3yξ)

=2x+3y-8

进而:

此即为所求问题的特解。

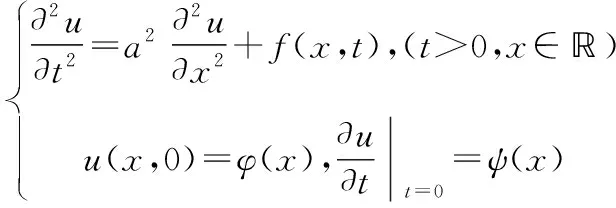
事实上提供了上述问题特解的积分表达式。应当指出的是，上述结论对二维和三维情形都是成立的。进一步，为便于计算，教材[11]给出了双曲算子的幂级数展开式，若F(x)为任意阶可微函数，则:

例5 求以下初值问题的特解。

(1)

解：问题(1)的特解可取为:

例6 求以下初值问题的特解。

(2)

解：问题(2)的特解可取为:

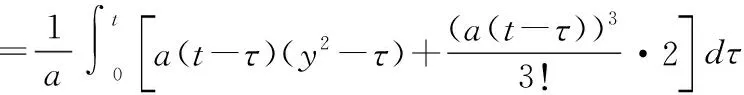
与文献[8-10]相比，本文提供的微分算子法适用于非齐次项含有两个变元的一般情形，突破了单变元的限制。进一步，由于微分算符的可运算性，该方法可应用于不同维数的波动方程的初边值问题。应该指出的是，若非齐次项仅为单变元的线性表达式，则可以通过直接积分法获得其特解。

例7 求以下初值问题的特解。

(3)

解：令uxx=uyy=uzz=0，则utt=2(y-t)，关于时间t直接积分两次，可得问题(3)的特解：

结语

本文通过对二阶常系数线性非齐次偏微分方程的系数和非齐次项的分类，给出了计算特解的直接积分法和微分算子法。值得强调的是，对于一些具有较特殊性质的变系数非齐次偏微分方程，也可采用类似的方法求取相应的特解。本文提供的方法具有较强的一般性和普适性，对今后的数学物理方程课程的教学具有一定的借鉴意义。