基于直线特征的合作目标加权位姿估计*

邢亚斌 王汝童 谭振国 郭永奇 于 涛

（北京化工大学信息科学与技术学院 北京 100029）

1 引言

随着我国高端制造业的快速发展，迫切需要对大型构件的三维几何参量进行高精度测量，以确保装配精度。当使用三维测量仪器对装配在大型构件表面的合作目标进行瞄准时，大型构件所处外界环境会影响合作目标的成像质量，导致其位姿估计精度较低，从而使测量精度降低。因此，研究合作目标加权位姿估计方法，减少外界环境造成的干扰，对提高合作目标位姿估计的精度具有重要意义和应用价值。

合作目标具有较为简单、明显的几何特征，且在3D世界坐标系中的坐标精确已知，有利于建立2D图像特征与3D合作目标之间的对应关系，位姿估计的复杂度低［1］。合作目标位姿估计方法主要可以分为基于n点透视模型（Perspective-n-Point，PnP）［2］和基于n线透视模型（Perspective-n-Line，PnL）［3］的方法。相比于点特征，直线特征所包含的属性更为丰富，而且提取较为稳定，受噪声的影响较小，可靠性高［4］，因此PnL问题受到了更为广泛的关注和研究。

根据PnL模型求解方法的不同，可分为非迭代方法和迭代方法［5］。其中非迭代方法主要有Mirzaei等［6］提出的全局最优线性求解方法，该方法将优化问题转化为对三个三次方程组的求解问题，简化了优化过程，但是由于麦考利矩阵的构建缓慢，总计算时间仍然较高；Zhang等［7］提出的RPnL方法，采用构建局部坐标系间接求取目标位姿的方法，简化了计算过程，其时间复杂度为O()n，位姿解算效率高，有效解决了直线共面情况下的位姿估计问题，能够得到较为准确的目标位姿初值。虽然非迭代方法的位姿解算速度较快，但是对直线特征提取的精度要求较高［8］。当合作目标图像受到测量环境影响发生质量退化时，会导致特征提取精度下降，非迭代方法的精度与稳定性都会受到较大影响［9］。

迭代法通过迭代的方式最小化特定的目标函数［10］，从而完成对位姿估计结果的优化，提高位姿估计精度［11］。此类方法能够通过准确的初值和层层的迭代提高位姿估计精度［12］。但是由于其迭代优化方法多为无差别优化［13］，并不能有效地解决由图像质量退化问题造成的直线定位偏差为位姿估计精度带来的影响［14～15］。张跃强等［16］提出的基于直线间积分距离度量的位姿估计方法属于无差别优化方法，认为每一条直线估计出的结果对误差的贡献相同来优化目标函数，会加大提取的相对不准确的直线对位姿估计结果的影响。针对该问题，张振杰等［17］为提高位姿估计的抗噪性，对每条直线进行加权，该方法假设权值服从高斯分布，并对其进行迭代优化，但是该权值具有一定随机性，并不能准确表示每条直线提取的精度。

本文在现有的PnL位姿估计方法的基础上，针对大型构件所处环境对合作目标图像成像质量造成的影响，在位姿估计过程中引入了直线端点特征的约束，提出了一种合作目标加权位姿估计方法。该方法根据直接提取的直线端点与其对应的通过几何约束关系计算的直线端点的距离赋予每条直线权值，在位姿优化过程中，根据每条直线的权值对其重投影误差进行加权，提高合作目标位姿估计的准确性，并保持较快的位姿估计速度。

2 基于直线特征的合作目标加权位姿估计

2.1 RPnL位姿估计方法

合作目标中普遍存在直线特征，采用RPnL方法［7］可以对其位姿初值进行求解，位姿估计的主要原理如下。

首先构建局部坐标系Om-XmYmZm，选择图像中具有最长投影直线长度的参考直线L0作为Zm轴，Xm轴为参考直线L0与相机光心Oc构成的投影平面Π的法向量n0，则Ym轴也可确定。世界坐标系Ow-XwYwZw旋转到Om-XmYmZm的旋转矩阵Rmw，可由V w0与V m0确定。其坐标系转换关系如图1所示。

图1 坐标系转换关系

另外选择图像中具有第二长投影直线长度的参考直线L1为辅助线，将线组{Li}分为n-2个三元组{L0L1Lj|j=2…n-2}，根 据 相 机 坐 标 系Oc-XcYcZc下直线li方向向量Vic垂直于法向量ni可得约束函数

式 中，Rcm=R′Rot(Xm，α)Rot(Zm，β)表 示 由Om-XmYmZm旋转到Oc-XcYcZc的旋转矩阵；R′为以n0为首列的随机正交旋转矩阵。由式（1）可得

式中，系数Ak、Bk可由计算得到。将sin2α=1-cos2α代入式（2），并令x=cosα可得

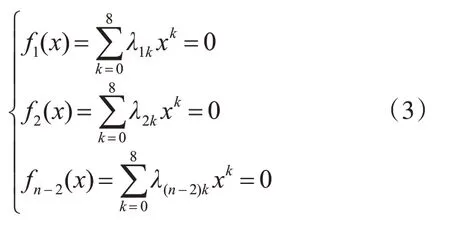
式中，系数λk可由n1、n2、V1m、V2m计算得到。

使用最小二乘残差法来求取系统的局部最小值可解得绕Xm轴旋转的角度α，则Rcm可简化为式中=R′Rot(Xm，α)，根据直线透视投影关系可得

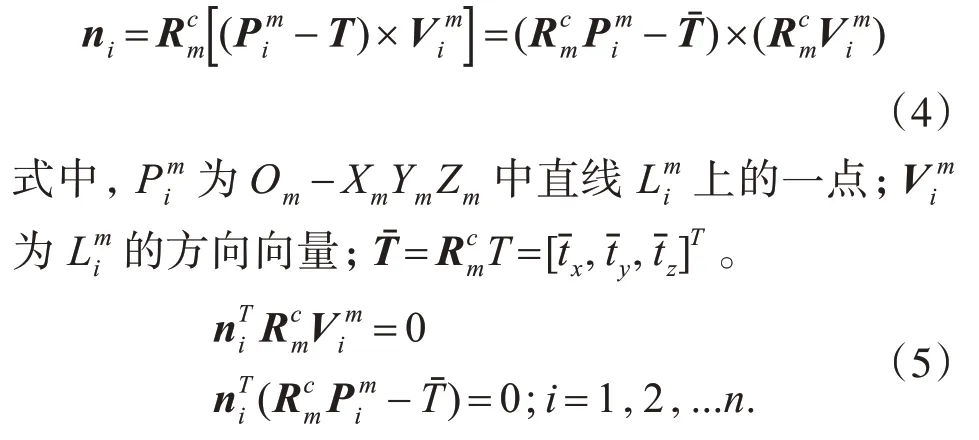
根据式（5），对于n条直线，可以得到2n个参数向量为[cosβ，sinβ，，1]T的齐次线性方程组如下所示：

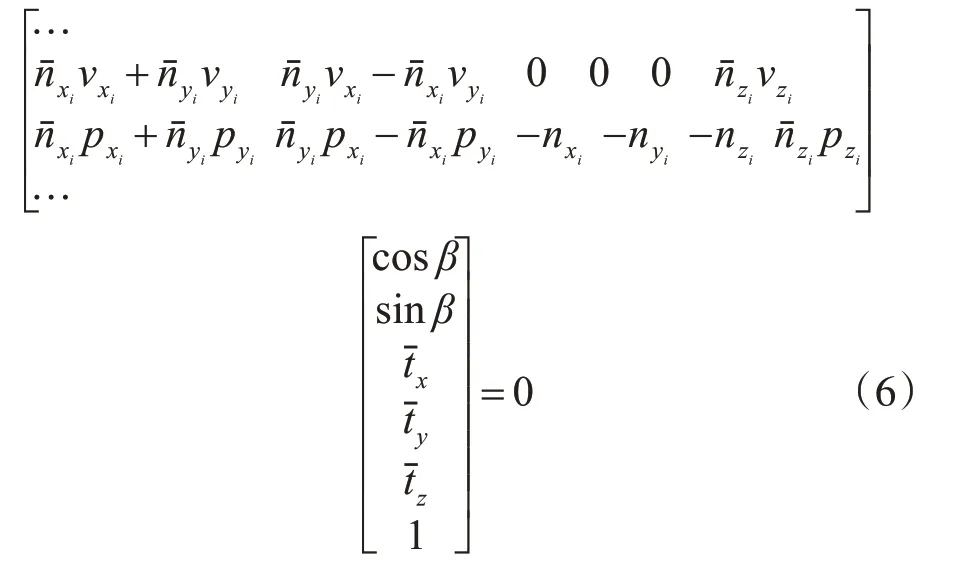
通过对齐次方程组进行SVD分解可以求出β和，从而可以计算出平移向量T=，最后可得到由Ow-XwYwZw旋转到Oc-XcYcZc的旋转矩阵=，即可求得目标对应的位姿参数矩阵M。

RPnL位姿估计方法对合作目标位姿初值进行了线性求解，但是该方法未经迭代优化，位姿估计精度有限，且易受干扰。

2.2 基于直线特征的合作目标加权位姿估计方法

采用RPnL方法获得合作目标的位姿初值之后，通过迭代方法对直线重投影误差进行优化，可以获得最优的位姿参数矩阵M。

本文所采用的合作目标为方形靶标（单个网格尺寸为62.5mm×62.5mm）和圆形靶标（内刻圆形直径为125mm），方形靶标中同时存在点、线几何特征，圆形靶标中同时存在点、线、圆几何特征，通过特征提取方法直接提取点特征，可以获得各直线的端点坐标；通过直线之间或直线与圆之间的几何约束关系，可以计算得到直线端点坐标。计算直接提取的直线端点到利用几何约束关系计算的对应直线端点的距离，可以确定直线特征提取的置信度。提取的直线和提取的点越接近则认为直线提取的置信度越高，所以在位姿估计的优化过程中，该条直线对应的权重大；而对于直线和点距离误差较大的情况，说明这部分提取的不好，那么则需抑制这部分对最终结果的影响，减少它的权重。

假设合作目标中有m条模型直线，表示为{L1，L2，…Li，…Lm}，直线的重投影距离可表示为模型直线Li的端点到投影平面Π的距离［16］，如图2所示。

图2 模型直线段端点到投影平面的距离

合作目标图像中的直线方程用极坐标表示为

将图像直线端点坐标代入式（7）可得

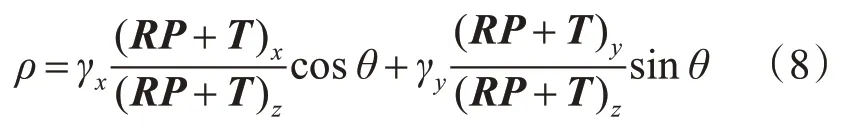
式中，γx、γy分别表示相机焦距与x轴、y轴方向像元尺寸的比值；式（8）可以简化为

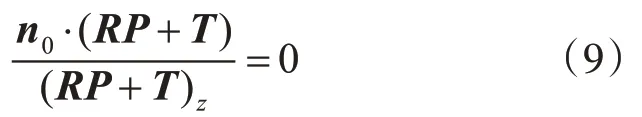
式中，n0=(γxcosθ，γysinθ，-ρ)T，其单位法向量可以表示为，则L在Π上的约束为

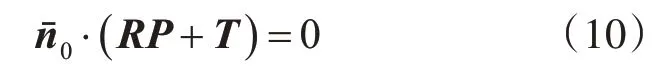
则L的端点到Π的距离为

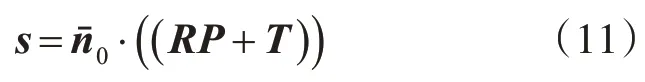
以最小化该距离为目标构建误差函数如下

采用引入直线权值的方法对误差函数进行改进，计算提取的直线端点到利用几何约束关系获得的端点的距离di，可确定直线权值，如下式所示。

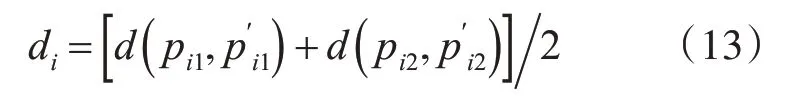
式中，(pi1，pi2)为图像中直接提取得到的直线端点坐标；()为利用几何约束关系计算得到的对应直线端点坐标。di越大则说明该条直线的提取置信度越低，则对应的权值越小。将di取倒数后归一化作为权值ωi，可得

则引入权值后的直线重投影误差优化的误差函数为

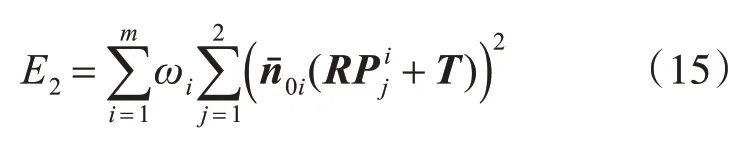
通过对其进行迭代求解，可得到最优的直线重投影误差，从而求解出对应的合作目标位姿参数矩阵M。

在合作目标的实际成像过程中，由于测量环境的影响会导致被测合作目标图像中可能存在噪声、模糊、光照变化等多种影响直线特征提取的干扰因素，而直线特征提取的精度会直接影响到基于直线特征的位姿估计的精度。所提合作目标加权位姿估计方法在优化重投影误差的过程中采用加权的方式引入每条直线的权值，可以提高合作目标位姿估计的准确性。

2.3 基于直线特征的合作目标加权位姿估计算法流程

本文提出的基于直线特征的合作目标加权位姿估计算法流程如图3所示，实现步骤如下。

图3 合作目标加权位姿估计算法流程框图

步骤1输入合作目标图像，相机内参数矩阵及畸变系数，设置最大迭代次数与误差阈值ε*。

步骤2提取合作目标图像中的几何特征，根据几何约束关系获取直线端点坐标，计算其与直接提取的对应直线端点的距离di，并将di的倒数归一化作为权值ωi。

步骤3构建局部坐标系，将每3条直线分为一组，计算由局部坐标系到相机坐标系的旋转矩阵Rcm，进而确定由世界坐标系到相机坐标系的旋转矩阵Rcw和平移向量T。

步骤4引入权值ωi构造新的直线重投影误差优化的误差函数E2。

步骤5将位姿初值代入目标函数，判断计算结果是否小于误差阈值ε*，若不满足，则继续迭代。

步骤6输出优化后的位姿参数。

3 实验与分析

实验所用图像为相机在真实环境下拍摄得到的多幅方形靶标图像（单个网格尺寸为62.5mm×62.5mm）和圆形靶标图像（内刻圆形直径为125mm），图像尺寸为3024×4032像素。对比实验为文献［7］的位姿估计方法。

实验采用重投影特征点平均距离误差与位姿估计时间作为位姿估计结果的质量评价指标，其中重投影特征点平均距离误差的计算公式为

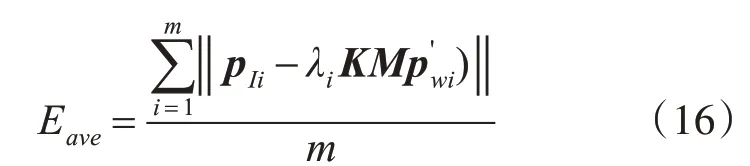
式中，pIi表示原2D特征点的坐标；表示3D特征点的坐标；M表示位姿参数；m表示特征点数量；λi表示任意的比例系数。

使用本文方法分别对3幅实拍的方形靶标图像与圆形靶标图像进行位姿估计处理，将所得到的位姿估计结果与文献［7］方法的结果进行对比，验证方法的有效性，图4为实验所用的合作目标图像。

图4 合作目标图像

合作目标图像的位姿估计结果如表1所示，对比位姿估计结果可以看出，本文位姿估计方法较文献［7］方法的精度有所提高，位姿估计时间与其相当。3幅方形靶标图像重投影特征点平均距离误差的平均值为4.9798pixel，位姿估计时间的平均值为0.193s；与文献［7］方法相比，重投影特征点平均距离误差的平均值减小0.3253pixel，位姿估计精度提高6.13%。3幅圆形靶标图像重投影特征点平均距离误差的平均值为3.4317pixel，位姿估计时间的平均值为0.189s；与文献［7］方法相比，重投影特征点平均距离误差的平均值减小0.3719pixel，位姿估计精度提高9.78%。

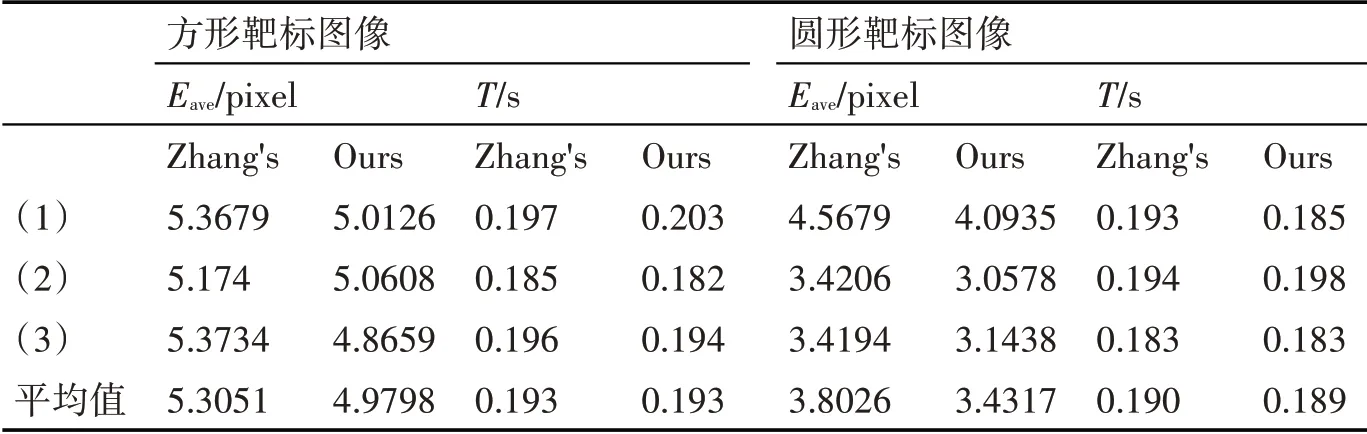
表1 合作目标图像位姿估计实验结果

通过对比实验所得到的位姿估计结果可以得出，本文方法的位姿估计精度在总体上优于文献［7］方法，能够提高合作目标的位姿估计精度，并保持较快的位姿估计速度。

4 结语

为了提高合作目标的位姿估计精度，实现三维测量仪器对合作目标的高精度瞄准，提出了一种基于直线特征的合作目标加权位姿估计方法。首先提取图像中的合作目标关键几何特征，通过几何约束关系获取各直线端点；然后计算其与直接提取的对应直线端点的距离，将距离的倒数归一化作为权值；最后将所得权值引入直线重投影误差的计算过程中构建新的误差函数，完成对合作目标位姿参数的优化。实验结果表明，所提方法的位姿估计精度优于文献［7］方法，方形靶标的位姿估计精度提高6.13%，圆形靶标的位姿估计精度提高9.78%，位姿估计时间与其相当，能够有效减小外界环境对位姿估计结果带来的影响，提高合作目标的位姿估计精度。