基于多谐振PR控制的并网逆变器相位补偿研究*
高文豪 陈 荣 阚加荣 王 涛
(盐城工学院 盐城 224051)
1 引言
并网逆变器是连接电网与光伏和风电输出能量的关键设备,并承担着重要功能。常用逆变器的输出滤波器有L型和LCL型,在电感总量相同的情况下,LCL滤波器具有体积小、成本低、高频衰减能力强等特点,普遍应用在光伏和风电网侧并网逆变器领域。但是引入LCL型滤波器会提高系统阶数,在谐振频率处存在较高的谐振尖峰,容易带来系统的不稳定[1~2],因此可以通过有源阻尼和无源阻尼[3]方法增加其阻尼使系统变得稳定。无源阻尼会增加功率损耗,有源阻尼常采用经典的电容电流反馈[4]。传统电流环外环主要有经典比例积分控制(PI)[5]、准比例谐振控制(QPR)[6]、重复控制(RC)[7]以及各种复合控制器相结合的控制方式,本文采用多谐振PR控制器的控制方式。随着更高的谐波补偿次数增加,往往致使系统相角裕量减小,导致了控制系统的不稳定。针对这个问题,文献[8]采用准PR控制器级联一个超前校正环节,既实现了对谐振频率进行相位补偿,又提高了系统相位。文献[9]在传统准PR控制基础上引入相位补偿,提高了电流控制器在谐振频率处的相角裕度,即使电网阻抗变化较大时,系统依旧可以保持稳定运行。
由于采样电容电流需要高精度的电流传感器,增加了系统成本。针对这个问题,许多学者开始通过使用更少的传感器达到相同有源阻尼的效果。文献[10]采用公共接入点电压反馈取代之前的电容电流比例反馈,有效抑制了谐振尖峰。文献[11]则提出了仅使用并网电流反馈可实现抑制谐振尖峰和并网电流的无静差跟踪。
本文在以上分析的基础上,首先搭建了并网逆变器数学模型,依据并网逆变器校正后的有源阻尼传递函数,推导出PCC电压反馈有源阻尼的反馈环节,最终选择一阶高通滤波器作为反馈环节。其次,介绍了多谐振PR控制器,伯德图表明控制器谐波补偿越高,系统的相位裕量下降的越快,间接导致系统不稳定。接着,引入相位补偿函数可以改善系统相位裕量,详细设计了相位补偿函数,通过对比加入相位补偿和未加相位补偿控制系统的伯德图,验证了加入相位补偿后,系统相位裕度有所提高,仿真证明了其有效性和可行性。
2 LCL型并网逆变器数学建模
根据直流侧供电电源类型不同,LCL并网逆变器划分为电压源型和电流源型[12]两大类。电压型逆变器控制方式简单、理论成熟,因此本文选择电压源型逆变器。图1为单相电压型LCL并网逆变器的主电路图及控制结构。弱电网阻抗一般由电阻和电感构成,由于考虑电阻后有助于并网系统的稳定,本文中只考虑弱电网最恶劣条件,即为纯电感条件下。Udc为直流侧输入电压,LCL滤波器是由逆变器侧电感L1、网侧电感L2和电容C三部分组成,用来滤除非线性元件产生的高次谐波。upcc代表PCC电压,将实际的电网等效为感抗Lg和富含特定奇次谐波电网电压ug串联。
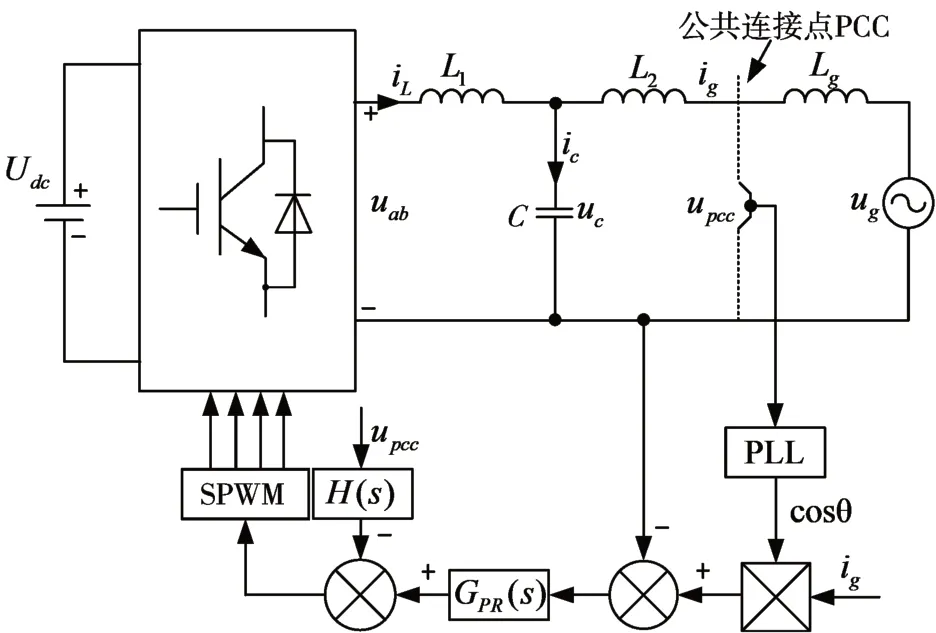
图1 LCL型并网逆变器主电路及控制结构
由图1可知,根据基尔霍夫电压定律(KVL)、基尔霍夫电流定律(KCL),列出交流输出回路电压、电流方程,之后进行拉普拉斯变换,可得:
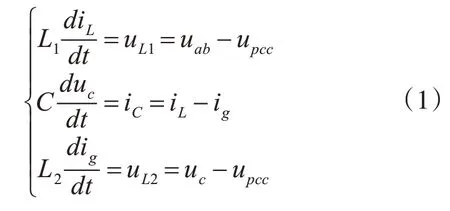
式中,uab、uc和ug分别为逆变器侧输入电压、滤波电容电压和网侧电网电压,iL、ic和ig分别为逆变器侧输出电流、电容电流和并网电流。根据式(1),得到s域LCL滤波器的等效控制框图,如图2所示。
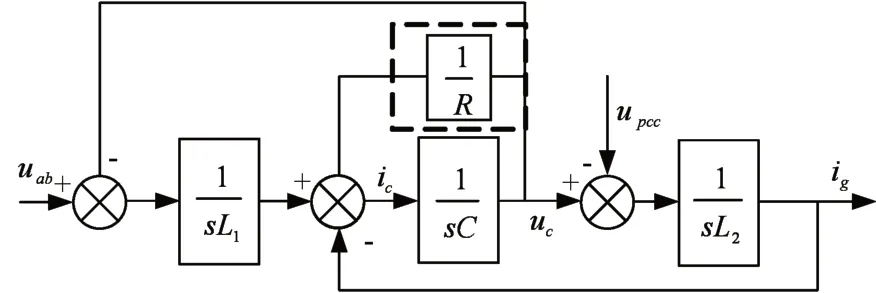
图2 LCL滤波器控制框图
其中,虚线框表示加入阻尼电阻,其中PCC电压upcc=ug+sLgig。逆变器输出电压uab到入网电流ig传递函数和电容两端并联电阻之后的传递函数表达式分别为式(2)和式(3):
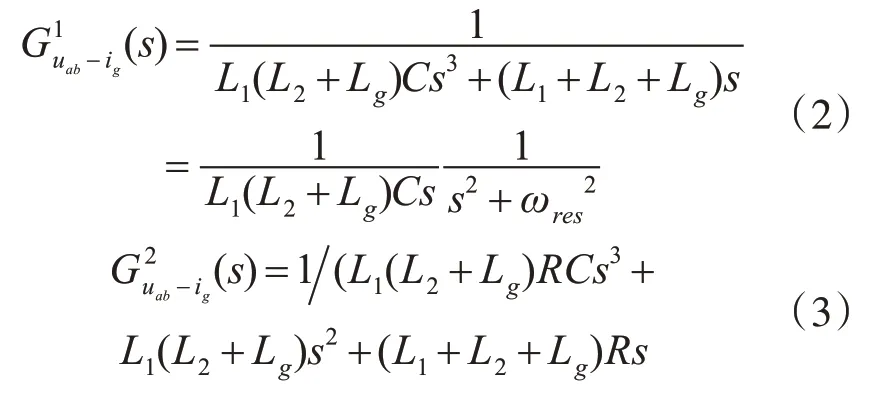
式(4)中,ωres为滤波器谐振角频率,其表达式为
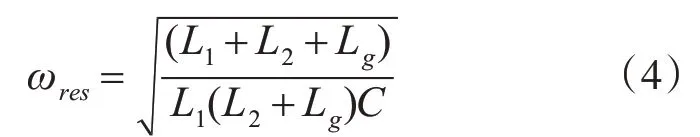
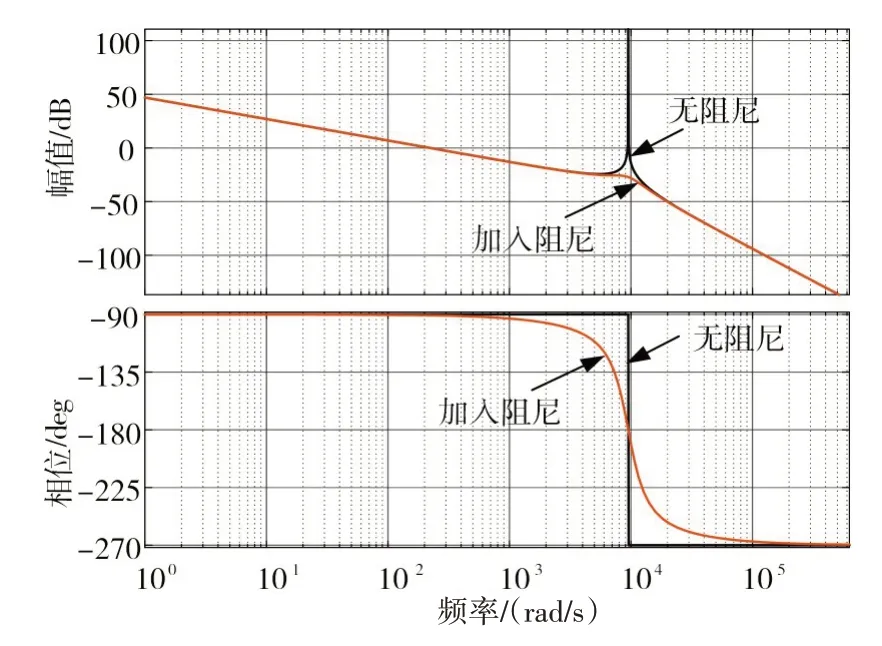
图3 并联阻尼电阻器后的频率特性
3 PCC电压有源阻尼分析
电容并联电阻,可以消除谐振尖峰。为了能有效抑制谐振尖峰和减少电阻对系统的损耗,本文采用有源阻尼的方法实现对谐振尖峰的抑制。传统电容电流控制需要高精度的电流传感器进行采样,为了避免引入额外传感器,本文采用基于PCC电压反馈。校正后传递函数表达式为
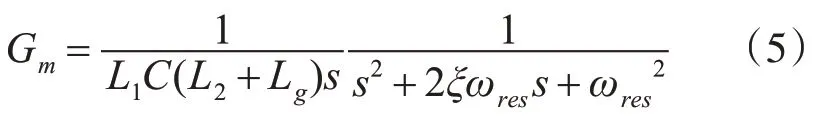
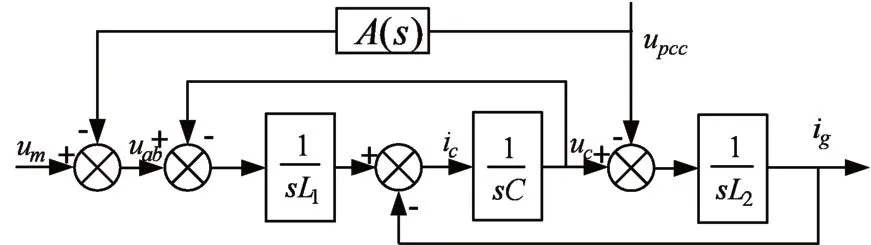
图4 PCC电压反馈有源阻尼控制框图
为了求出PCC电压反馈有源阻尼所需的反馈环节,推导um到ig的有源阻尼传递函数为
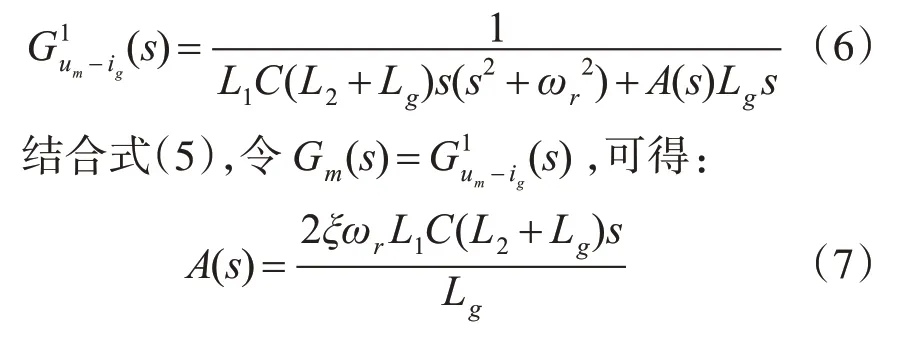
式(7)给出了A(s)为一阶微分环节。PCC电压需要一阶微分器才可以实现有源阻尼。但是实际控制过程中,无论采用模拟或数字控制,微分环节难以实现[14]。从频率特性分析,微分环节容易对高频信号进行线性放大。因此,采用一阶高通滤波器代替微分环节。一阶高通滤波器传递函数表达式:

式(8)中,kc和ωh为一阶高通滤波器环节的反馈系数和截止频率。本文使用文献[10]中的参数计算方法,即ωh=ωres,kc=0.1。因此,加入一阶高通滤波器后um到ig的传递函数为
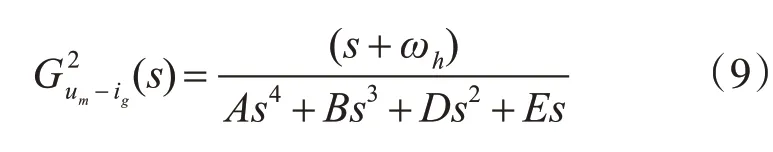
式中:
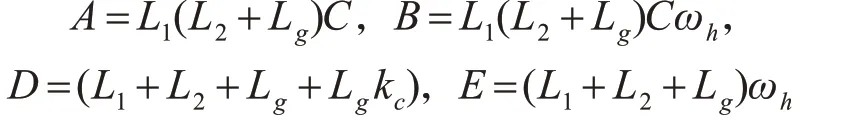
根据式(6)与式(9)分别绘制微分和高通滤波器(HPF)反馈环节的伯德图,如图5所示。
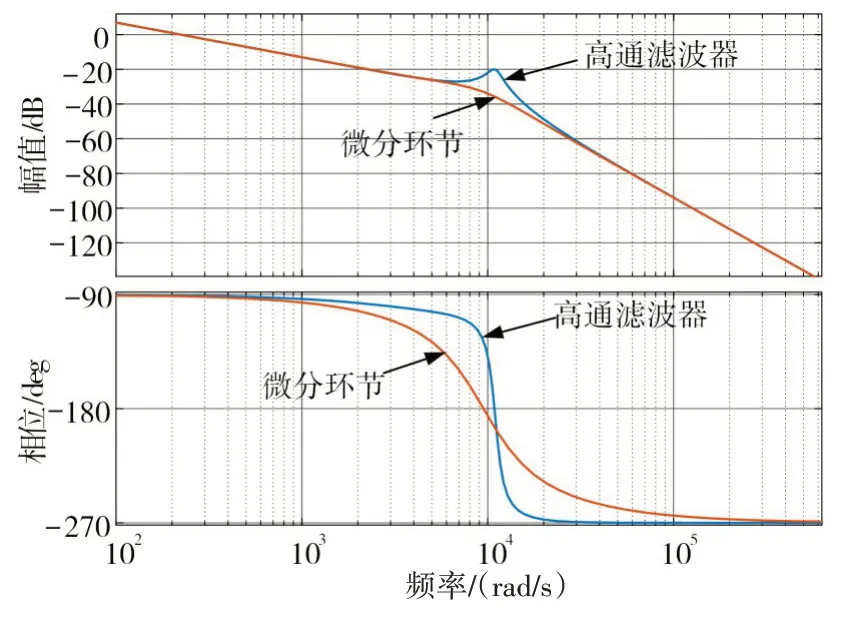
图5 微分环节和HPF有源阻尼频率特性
从对数幅频特性图可以得到,微分环节和高通滤波器谐振频率处的尖峰增益都在0db以下[15],微分环节在谐振频率处的尖峰完全被削弱了,而高通滤波器有源阻尼谐振还带一点谐振尖峰。另外,从相频特性图来看,在谐振频率附近,微分环节相位下降速度明显大于高通滤波器。综合以上分析,选择高通滤波器替代微分环节,可以显著地抑制谐振尖峰。
4 带相位补偿的多谐振PR控制器分析
4.1 多谐振PR控制器设计
多谐振PR控制器的传递函数:

kp为比例环节系数,kr为谐振频率系数,ω0为基波角频率,ωc为多谐振PR调节器的截止频率。鉴于背景谐波中3、5、7次含量较多,因此本文只考虑电网电压富含3、5、7次谐波。根据Matlab绘制其伯德图,本文选取kp=0.4,ωc=π,ω0=π,其频率特性如图6所示,其中最高补偿为7次。
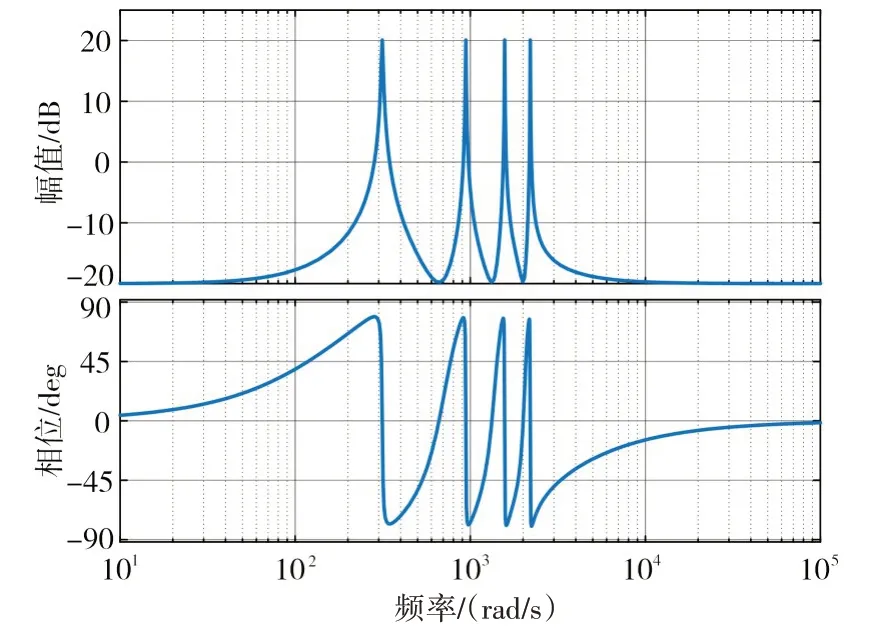
图6 电流控制器伯德图
从相频特性图来看,当控制器在基频、3、5、7次谐波频率处,存在约180°相角跳变现象,但当需要补偿的谐波次数增加时,会减少控制系统的相角稳定裕度。为了改善控制系统相角裕度,本文采用多谐振PR控制器与相位补偿器相结合方式。此校正环节可以极大地提高准PR控制器在谐振频率处的相位,幅值裕度基本保持不变。
4.2 改进策略分析
引入相位补偿环节[16]的开环传递函数表达式如下:
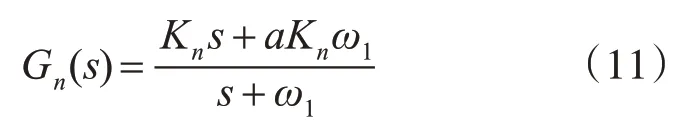
最大超前角与最大超前角频率[8]分别如式(12)、(13)所示:
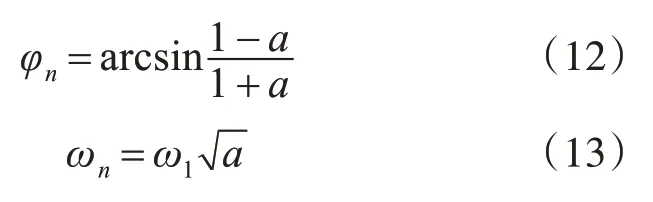
为了降低超前环节对控制系统开环传函幅频特性的影响,ωn一般设置为需要补偿的最高次谐波频率处,本文最高谐波补偿次数为7次,即ωn=2*π*350,φn取 值 范 围 为10°~30°,选 取φn=20°。参数Kn的选择方面,可令Gn(jωn)=0,经计算Kn=1.4。根据式(11)~(13)计算可得,ω1=3200,a=0.5。图7为相位补偿传递函数的伯德图,分析可知,当频率为2*π*350时,相位约为20°,幅值增益基本不变,可以很好补偿7次谐波产生的相角滞后问题。
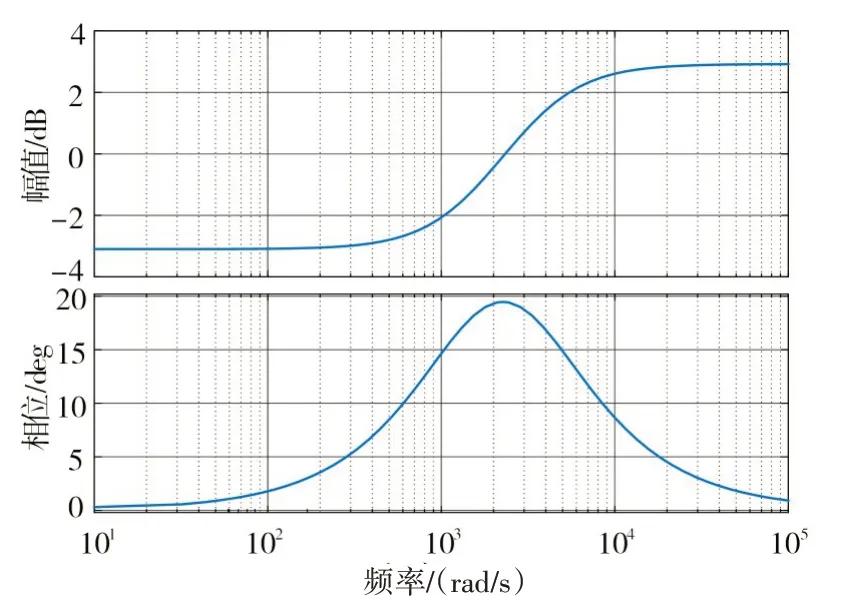
图7 Gn(s)伯德图
图8为双闭环控制框图和PCC电压前馈图,通过对结构图的等效变换和化简,带谐波补偿的准PR控制器的开环传递函数表达式如下:
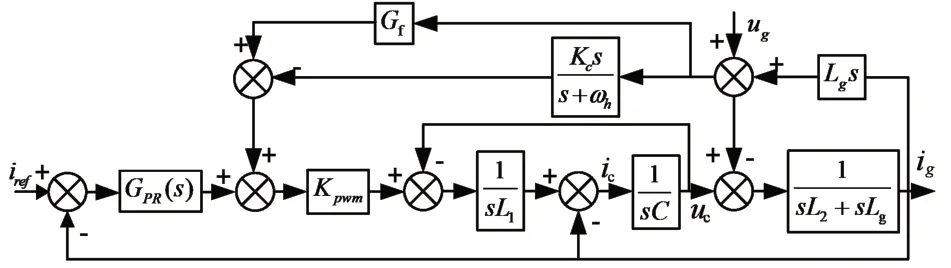
图8 基于组合控制的系统结构框图
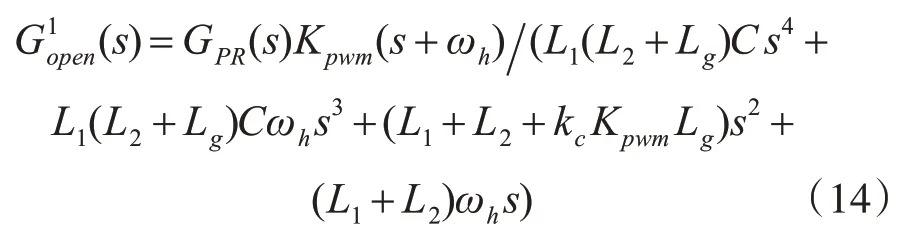
加入相位补偿环节后,整个控制系统开环传递函数表达式为
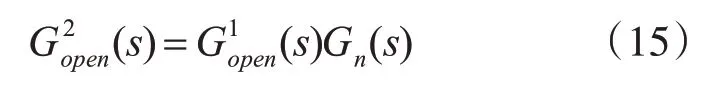
图9分别为仅使用带谐波补偿的准PR控制器伯德图和加入串联相位补偿环节后的伯德图,由图可知,未加相位补偿环节之前,7次谐振频率处对应的相位接近负180°,会带来系统稳定性问题。而当采用相位补偿环节对3、5、7次谐振频率点补偿一定角度后,相频曲线整体上移,相位补偿后的控制系统相角裕度原来的26.2°增加到44.3°,而在基波频率和3、5、7次频率附近仍有较大增益。
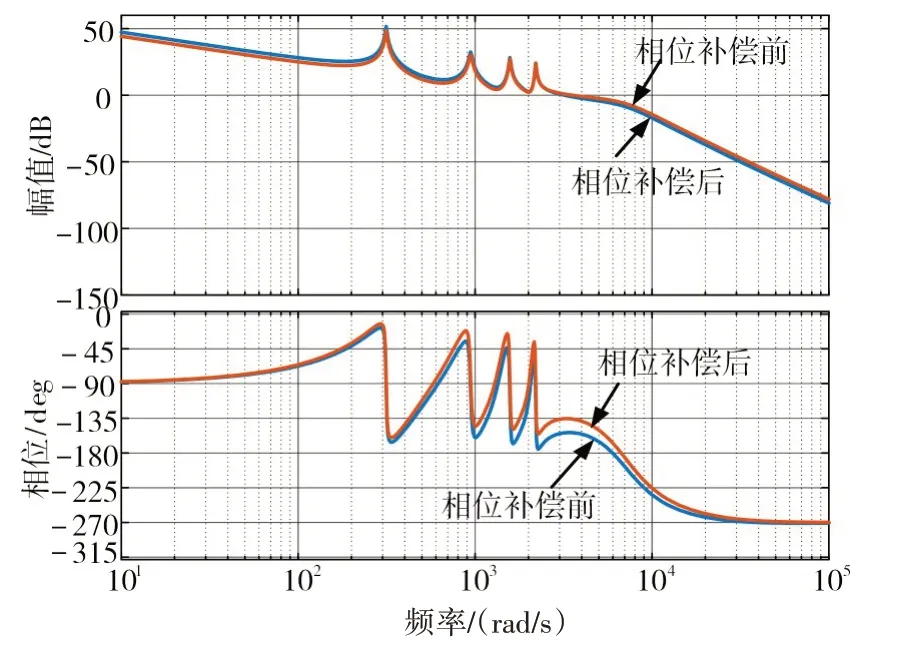
图9 开环传递函数伯德图
5 仿真与分析
通过Simulink仿真工具搭建单相LCL并网逆变器模型,采用如图1所示的电路拓扑,以验证系统方案的有效性和可行性。得到仿真波形如图10~13。系统中主要仿真参数如表1所示。
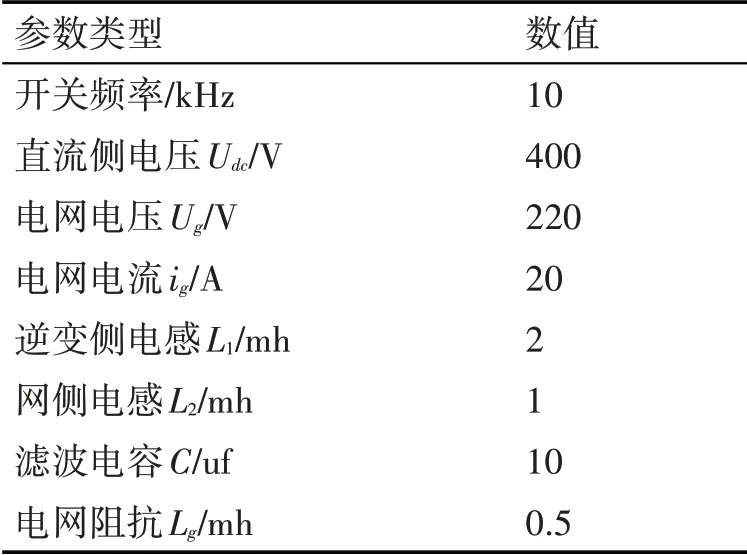
表1 仿真主要参数
仿真结果如图10~13。
图10给出了入10%的3次谐波、5%的5次谐波时和5%的7次谐波[17],入网电流与电网电压几乎不存在相位差,并且波形较为理想。图11为并网电流的频谱图,THD为0.38%,说明采用多谐振电流调节器有效抑制了谐波和PCC电压反馈有源阻尼的有效性。图12表示在0.12s时,给定的参考电流由20A升高到25A,电流存在小的扰动,但是波形很快达到稳态,具有较快的动态性能。图13(a)和(b)是未加入和加入相位补偿环节的波形图,如图13(a)所示,当Kp=0.069时,相对正常值取值变小,采用多谐振PR控制器对入网电流进行控制,THD=5.8%>5%,大于了并网电流参考标准,波形发生严重畸变。图13(b)为加入串联校正环节后,THD为1.95%,电流波形质量得到改善,增强了系统的稳定性。
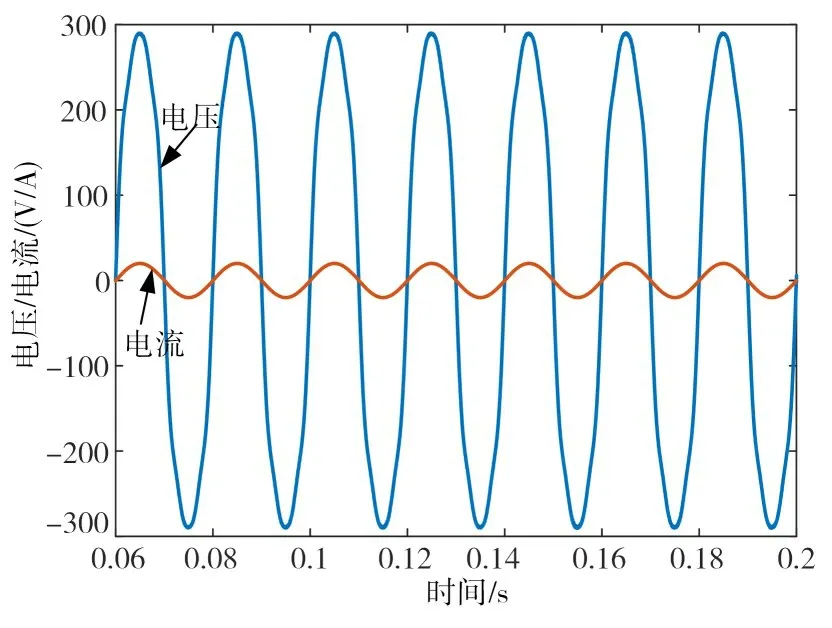
图10 注入谐波后,电流和电压波形
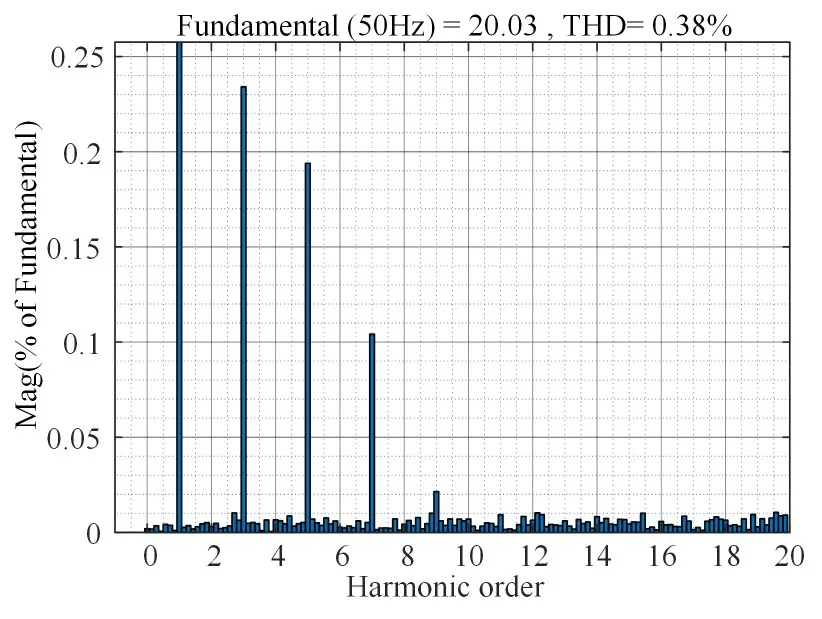
图11 并网电流FFT频谱图
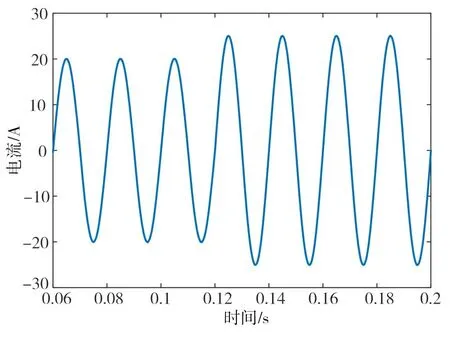
图12 参考指令突变,电流波形图
6 结语
本文采用外环为并网电流,内环为PCC电压反馈双闭环控制策略,在Simulink搭建仿真模型,验证本文理论的正确性,得到以下结论:
1)相比常规的电容电流比例有源阻尼反馈,本文采用的PCC电压反馈,可以省去高精度电流传感器,而且当电流突变的情况时,还能有效抑制高频下产生的谐振尖峰,仿真表明此方法的有效性。
2)针对多谐振PR控制会随着谐波补偿次数增加会引起相角滞后问题,在此基础上串联相位超前补偿环节,改善了整个系统的相位裕量,增强了系统的稳定性。

