基于8-邻域和曲率的多阶偏微分方程混合去噪*

孟东东 周先春 王文艳 杨传兵 汪志飞 吴晓慧

（1.南京信息工程大学电子与信息工程学院 南京 210044）（2.南京信息工程大学人工智能学院 南京 210044）

1 引言

在图像去噪研究过程中，目前常用的传统去噪算法是偏微分方程图像去噪。偏微分方程算法通过图像本身邻域像素点之间的关系建立数学方程模型，并求出方程最优解获得去噪图像。但低阶偏微分方程ID［1］、PM［2］、TV［3］模型会产生边缘模糊或“阶梯效应”。有学者为避免边缘模糊提出将水平集曲率和梯度作为模型中的边缘检测因子，加强边缘锐化［4］。有学者提出四阶偏微分方程YK［5］模型。四阶偏微分方程虽然能抑制“阶梯效应”的产生［6］，但会产生“斑点效应”。对此，研究人员在偏微分方程模型上不断改进以提升去噪性能。文献［7］在各向异性滤波中提出新的扩散系数；文献［8］利用时间-分数导数顺序控制时间分数扩散方程的扩散过程；文献［9］将BM3D和偏微分方程结合，避免人为效应和偏置效应；文献［10］将二阶、四阶偏微分方程模型结合（MBM模型）以实现将其各自的优点相结合并规避其各自的缺点；文献［11］通过全局稀疏梯度模型（GSG）解决传统梯度算子对噪声敏感导致伪像的问题；文献［12］建立梯度和曲率双驱动函数，并将双驱动函数引入TV模型以提高图像去噪性能；文献［13］将偏微分方程去噪的先验知识和卷积神经网络的训练相结合，以训练出去噪性能更好的去噪模型。

本文所提出新模型在二阶和四阶偏微分方程混合使用中利用隐式曲率构造自适应权重函数控制两类偏微分去噪时比例，有效避免边缘模糊和“阶梯效应”的同时进一步保护图像细节特征和边缘细节。

2 相关算法理论

假设图像的噪声模型为

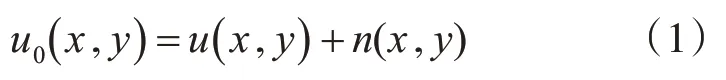
式中：u0(x，y)是含噪图像，u(x，y)是原始图像，n(x，y)是高斯噪声。

2.1 ID模型

ID去噪模型如式（2）所示：

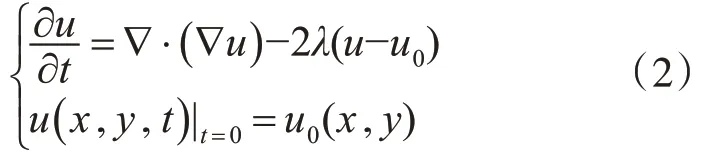
式中：λ是拉格朗日乘子，∇表示梯度。

由于各向同性扩散去噪模型扩散系数是1，所以扩散在所有方向是相同的，这虽然能够去除噪声，但会导致边缘模糊。

2.2 PM模型

Perona和Malik提出了各向异性扩散模型［14］，Weickert［15］使用能量函数得PM模型：

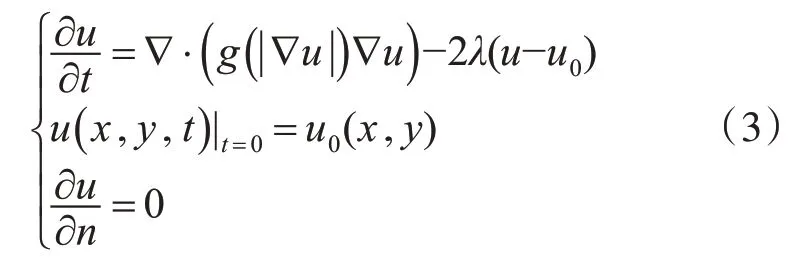
因为在式（3）中不能保证解的唯一性，所以PM模型是一个病态模型，当噪声和边缘具有相同梯度时，PM去噪效果不佳。

2.3 TV模型

TV去噪模型：

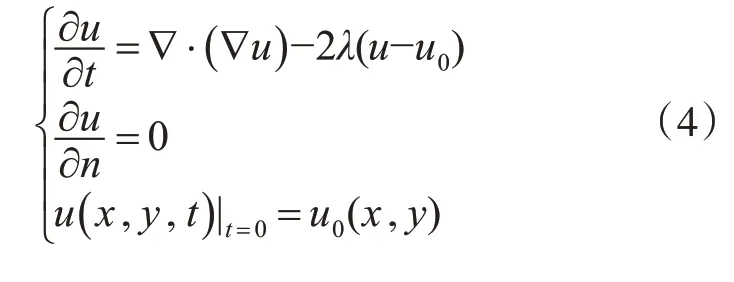
式中：λ控制保真项和正则化之间的权衡［16］。TV模型具有良好的边缘保持和图像平滑性能，但在平滑区域会产生“阶梯效应”。

2.4 高斯曲率滤波

高斯曲率滤波是曲率滤波［17～19］中最常用滤波方式之一，通过假设原始图像构成的曲面是分块可展的，达到边缘保护的作用。

高斯曲率能量公式：

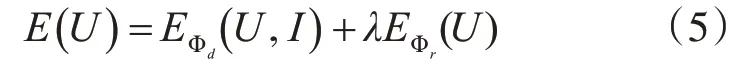
式中：E是总能量，EΦd是数据拟合项，用于度量返回图像U和输入图像I的匹配程度，EΦr是正则能量项，λ是正则能量的权重。

3 新模型

为解决二阶偏微分方程图像去噪时产生的阶梯效应，考虑到四阶偏微分方程在图像光滑区域消除阶梯效应的能力，本文提出基于8-邻域和隐式曲率的多阶偏微分方程混合去噪方法，利用8-邻域和隐式曲率构造权重函数去控制两类方程在图像去噪时的比例，实现二阶偏微分方程和四阶偏微分方程的自适应调整去噪，将其各自优点最大化。

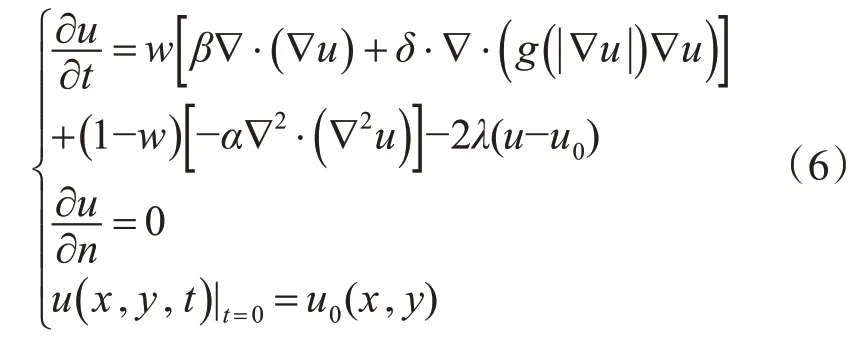
式中：∇是梯度算子，||∇u是梯度u的模，u是原图像，u0是含噪图像，w、β、δ、α是权重函数。λ是保真项控制函数，g(||∇u)是扩散函数。

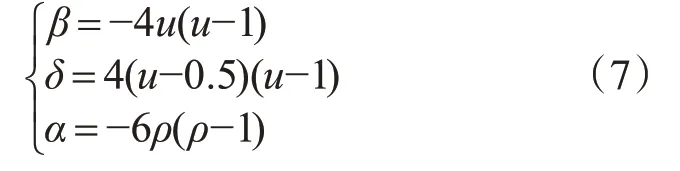
其中u、ρ是以图像梯度和拉普拉斯算子为自变量的函数：

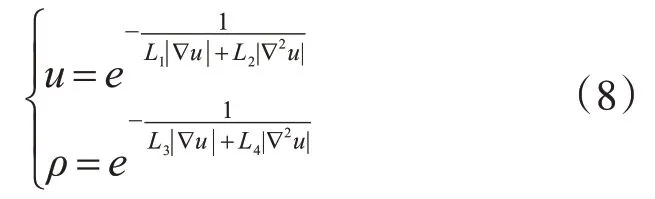
式中：L1、L2、L3、L4是固定值。

式中：q是固定值，ν是图像某一中心元素及其8-邻域元素的均方差，d是中心元素到8-邻域元素切平面的最小距离。本文为了保护图像的边缘信息，通过直接调整各点像素值使其位于8-邻域像素的切平面去满足分段可展的假设，实现隐式使用图像曲率信息，并采用最小距离原则，在8-邻域像素组成的切平面中，寻找与当前中心像素距离最近的面，对像素进行调整。避免显示计算图像曲率所需图像二阶可微的条件，达到减少计算复杂度的作用［20］。式（11）中：k为门限阈值，用于区分平坦区域和边缘。

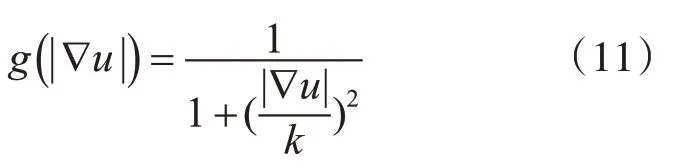
为了更好使用图像曲率信息，新模型选用8-邻域为最小切面构造区域并使用半窗切平面组合和最小三角切平面组合作为基础投影算子，将8-邻域分成4种半窗三角切平面和4种最小三角切平面；使用局部方差作为区分边缘和平坦区域的边缘检测因子。

4 实验结果分析

利用Matlab仿真软件进行噪声去除分析，验证新模型的可靠性，本文采用峰值信噪比（PSNR）、平均绝对误差（MAE）、结构相似性（SSIM）指标去评价去噪效果，与PM、TV、ID、MBM模型进行对比。

PSNR定义如式（12）所示：

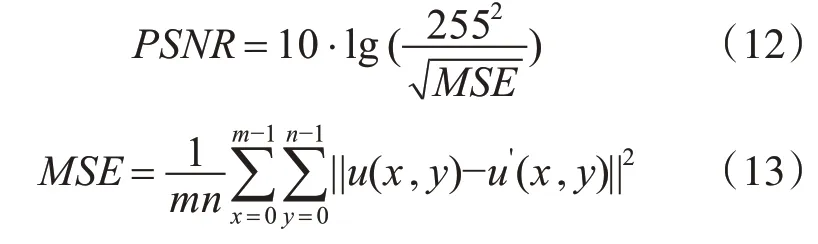
式中：u(x，y)代表原始图像，u′(x，y)代表去噪后图像，m、n分别代表图像尺寸中的行数和列数。峰值信噪比PSNR越大越好。

MAE定义如式（14）所示：

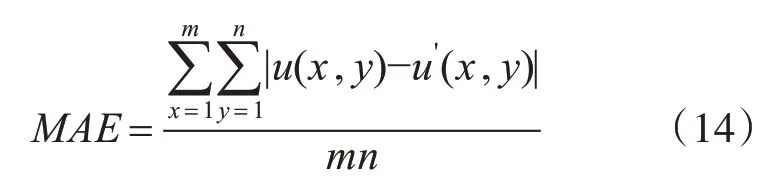
MAE是绝对误差的平均值，其值越小表示与原始图像的偏差越小，图像质量越好。

SSIM定义如式（15）所示：

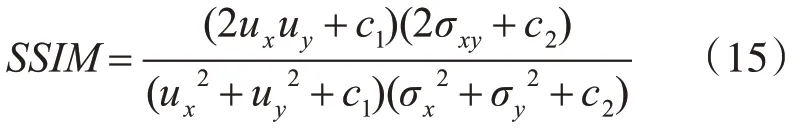
式中：ux和uy分别是样本x和y的均值，σx2和σy2是样本x和y的方差，σxy是样本x和y的协方差。c1和c2是常数用来避免除零。结构相似性SSIM∈（0-1），去噪后图像和原图像越接近SSIM值越大。

图1是ZX、Cameraman、Barbara的原图，图像像素分别为512×512、256×256、512×512。图2是添加了标准差为20的高斯噪声的ZX、Cameraman、Barbara含噪图像。图3～图5是TV、PM、ID、MBM模型和新模型对图2进行去噪后得到的效果图（图像左上角均为局部细节放大图）。

图1 Lena、Cameraman、Barbara原图

图2 Lena、Cameraman、Barbara加噪图

图3 不同模型去噪效果图

图5 不同模型去噪效果图

图3（c）整体去噪效果较好，但棕熊鼻子处出现了边缘模糊，这是因为ID模型无法有效区分图像边缘和平滑区域，在平滑区域存在“过平滑”；从图3（a）的整体上可以看出棕熊影子和地面以及防护栏和防护栏后面的树木形成了明显的“阶梯效应”；图3（b）较图3（a）、（c）在棕熊鼻子处的细节特征保护的更加完善，但在棕熊的嘴角处存在边缘混叠，这与PM是病态的模型有一定的关系；图3（d）中棕熊鼻子上方的轮廓较图3（b）更加明显；图3（e）较图3（d）不仅在棕熊鼻子上方轮廓更加清晰，而且鼻孔处的轮廓也更加明显，这是因为新模型通过图像的细节信息构造权重函数控制去噪时二阶、四阶偏微分方程比例，能充分利用图像的细节信息，将二阶、四阶偏微分方程各自优点最大化。

观察比较图4中Cameraman面部和后方建筑物轮廓、图5中Barbara头巾条纹和手掌边缘轮廓发现，新模型较其余4个模型对图像边缘结构细节具有更好的保护作用。

图4 不同模型去噪效果图

本文中L1、L2、L3、L4分别取1/20、1/40、1/50、1/25，k=15，q=0.001。原始图像加性噪声参数分别为标准差为σ=15、20、25的高斯噪声。

表1、2、3为 不 同 去 噪 模 型 的PSNR、MAE、SSIM。观察表1、2、3，新模型较TV、PM、ID、MBM模型PSNR、SSIM值最大，MAE值最小。在σ=15、20、25时，ZX图PSNR增 大0～1.7dB，SSIM提 升0.01～0.03，MAE降低0.06～2.56；Barbara图PSNR增大0.27～0.95dB，SSIM提 升0.01～0.08，MAE降 低0.14～2.72；Cameraman图PSNR增 大0.41dB～2.18dB，SSIM提升0.01～0.24，MAE降低0.43～3.53。

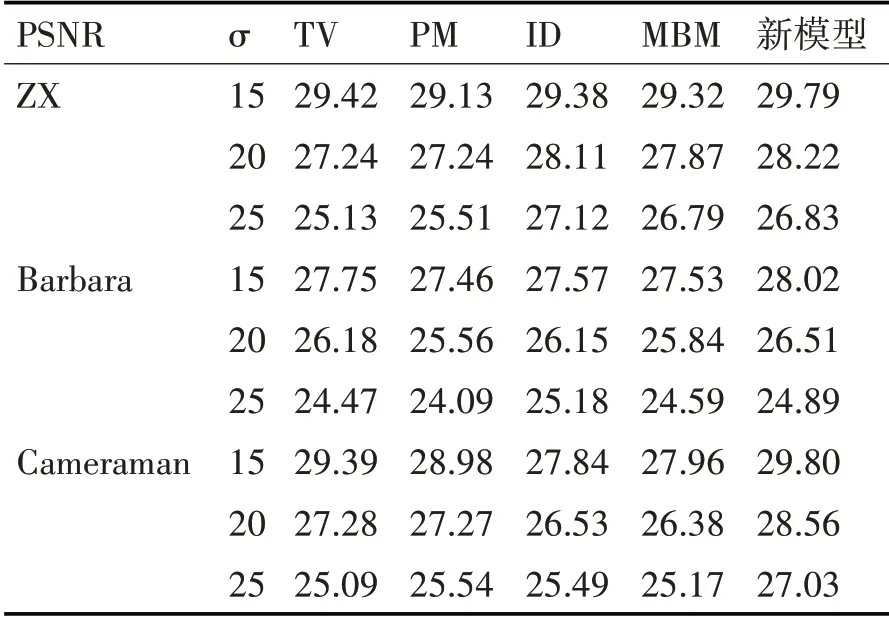
表1 不同去噪模型的PSNR

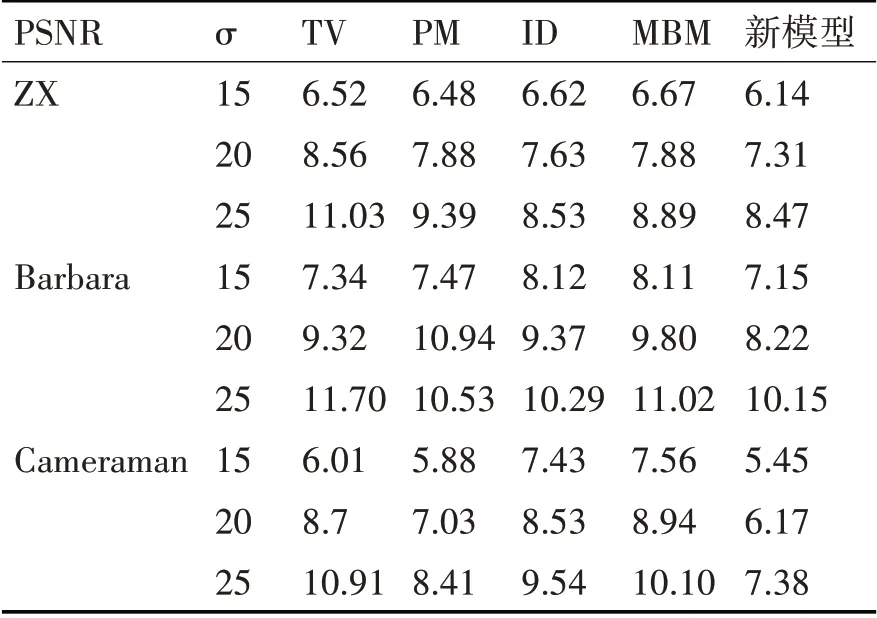
表2 不同去噪模型的MAE

新模型不仅有较好的PSNR、MAE、SSIM值，更能对于图像边缘结构信息保护的更加完善，无论是从图像去噪效果上看，还是从去噪性能对比上看，本文都具有更加理想的去噪性能。

5 结语

本文提出的新模型通过将二阶、四阶偏微分方程混合使用，规避某一种方程单独去噪时会产生的缺点，将其各自的优点最大化，并通过图像中任意一中心元素及其8-邻域像素的关系，将隐式使用的曲率作为边缘检测因子，实现偏微分方程根据图像曲率信息自适应调整权重函数w，从而自适应调整二阶、四阶偏微分方程的去噪比例。

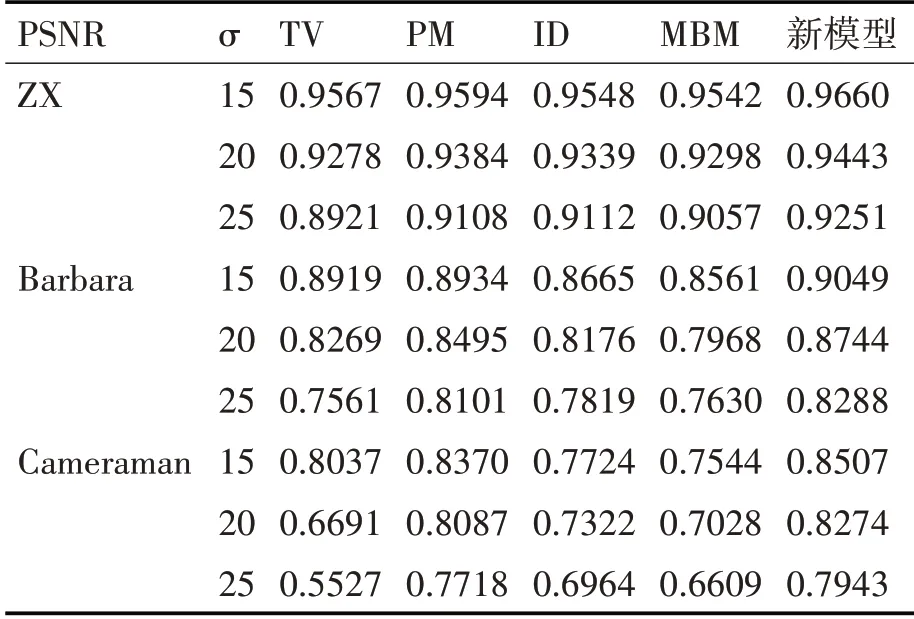
表3 不同去噪模型的SSIM

实验结果表明新模型相较其他算法有较大改进。新模型相较二阶偏微分方程图像去噪可以避免边缘模糊和“阶梯效应”；相较四阶偏微分方程图像去噪可有效抑制“斑点效应”；相较其他混合偏微分方程图像去噪，新模型具有更好的PSNR、MAE、SSIM值。