邻域贪婪的Harris鹰优化求解立方体表面MTSP问题*

徐浏凯 苏守宝，3 何 超

（1.南京邮电大学计算机学院 南京 210023）（2.金陵科技学院数据科学与智慧软件江苏省重点实验室 南京 211169）（3.江苏科技大学计算机学院 镇江 212003）

1 引言

旅行商问题（Traveling Salesman Problem，TSP）作为一个经典的路径规划问题，在工程领域和计算机科学领域中得到了广泛的应用和研究。TSP问题定义为：假设有一个旅行商人要访问n个城市，每个城市只能访问一次，且最后要回到原来出发的城市。此问题的主要目的是使成本、时间和路径等参数最小化。近年来，随着对TSP的深入研究，三维空间中的TSP问题得到了广泛的研究与关注。例如：航空公司飞行路线规划［1］、卡车路径规划［2］、计算机网络通信路径规划［3］等。因此，针对现实中的规划问题提出有效的TSP解决方法显得愈发重要。针对此需求，国内外相关研究人员提出了许多解决方案，这些方案大致可分为精确方法和启发式方法两类。精确方法主要包括迭代改进、分支定界和分支切割等方法TSP［4～5］，而启发式技术主要是基于模拟退火，禁忌搜索等［6～8］方法来解决。为了获得更好优化效果，研究者们提出了一些混合进化算法［9～10］。此外，文献［11］还使用硬件方面的GPU并行计算技术来提升群智能算法在该类问题上的求解速度。

文献［12～14］提出了一种3D几何形状（如球体和长方体）上的TSP问题。与经典TSP不同，此类TSP问题中所有坐标点都位于一个球体或长方体上，并且点之间的路径需要在球体或长方体表面上进行计算。目前针对此类问题，研究人员们使用了粒子群算法（Particle Swarm Optimization，PSO）等群智能算法［12～14］进行了有效的研究。而本文的主要研究是采用一种较新的群智能算法Harris鹰群优化算法对立方体上的多旅行商问题进行求解。

Harris鹰群优化算法［15］（Harris Hawks Optimization，HHO）是受到了Harris地区的猎鹰围捕猎物（兔子）和猎物相应的逃跑行为的启发而产生的一种新的群智能算法。该算法具有参数较少，易于实现等优点，已被应用于多种寻优问题求解。

多旅行商问题（Multiple Traveling Salesman Problem，MTSP）是经典旅行商问题的一种推广。该问题在实际应用中往往考虑的影响因素较为复杂，且只考虑旅行商路径总长度最小化可能会造成路径的不均衡。针对以上问题，本文在前人研究基础上将改进的Harris鹰群优化算法。在本研究中，首先会给出立方体表面上两点的距离计算公式，然后针对立方体表面的MTSP的不同特点，将k-mean聚类，邻域搜索算子和贪婪策略等改进方法与HHO结合提出了一种邻域贪婪的Harris鹰优化算法（Neighborhood Greedy Harris Hawks Optimization，NGHHO），并在TSP benchmark测试集和随机点集上分别进行了多次测试以验证NGHHO的算法性能，最后与其他几种群智能算法在最优路径搜索性能上进行了比较。

2 问题与方法

2.1 立方体表面的MTSP问题

立方体是一种常见的几何形状，生活中诸多的物品如书籍、橱柜、家具和建筑物等很多都是立方体。它们都具有六个面、十二个边和八个角，如图1所示。

图1 立方体

立方体MTSP问题可以定义为：m位在能够在立方体表面移动的旅行商要向该立方体表面的n个城市贩卖自己的商品，如何选择一条最优的路径，使得m位旅行商从立方体上的m个城市出发，经过所有城市有且仅有一次，且其所有走过的路均在该立方体表面上，所有旅行商所旅行的总路程要求最短。在现实生活中，解决该类问题可用于室外爬墙机器人，大厦外的无人机路径规划、建筑物外壁的自动清洁机器人的路径规划等方面。举例来说，当摩天大楼发生火灾且无法触及楼层和房间时，为了运送救援物资爬墙机器人便会在建筑物表面上方移动，此时爬墙机器人就需要一条较好的路径规划，以更快地赶到需要救援的地点。

2.2 立方体表面的任意两点最短距离

立方体表面的任意两点的距离计算与普通的平面上的计算存在一定的区别。距离计算需要考虑三种情况，即两点处于同一平面上，两点处于对立面上，两点处于相邻面上。三种情况的距离计算公式如下：

假如两点处于相同面上，此时，距离计算等价于平面情况的计算。点i到点j的距离方程为

假如两点处于对立面上，此时需要考虑四种情况，点i可能从周围的四个面中的任意一个面经过到达点j，所以计算时需要将四种方式得到的距离都计算出来，最后将四个距离进行比较，其中的最小值是两点间的最短距离。以下面-前面-上面这种情况如图2（a）所示，其公式如下：

假如两点在相邻面上，此时需要考虑三种情况，点i到点j可能的路径如图2（b）所示。假设点i在前面，点j在上面，那么就存在前面-上面、前面-左面-上面、前面-右面-上面三种路径。此时，也需要将三种情况的距离求出，然后取三个距离的最小值作为两点间真正的最短距离。

图2 最短距离

1）前面-上面情况的计算公式

2）前面-左面-上面情况的计算公式

3）前面-右面-上面情况的计算公式

2.3 HHO算法

HHO算法受到鹰捕食行为以及兔子（即猎物）的逃跑行为的启发，构建了鹰基于不同策略捕猎兔子的数学模型，使鹰群在栖息和捕猎过程中逐渐接近猎物，即最优解。该算法具有易于实现，参数较少等优点。算法中的种群迭代部分由三部分组成：探索阶段，从探索到开发的过渡阶段，开发阶段。

1）探索阶段

该阶段中，HHO算法模拟了鹰的栖息行为。从搜索角度来看，该阶段主要进行全局探索，由两种不同的策略组成，即基于鹰群中某一只鹰的位置进行栖息的策略和基于在搜索范围内随机位置的进行栖息的策略。两种策略的具体数学形式为

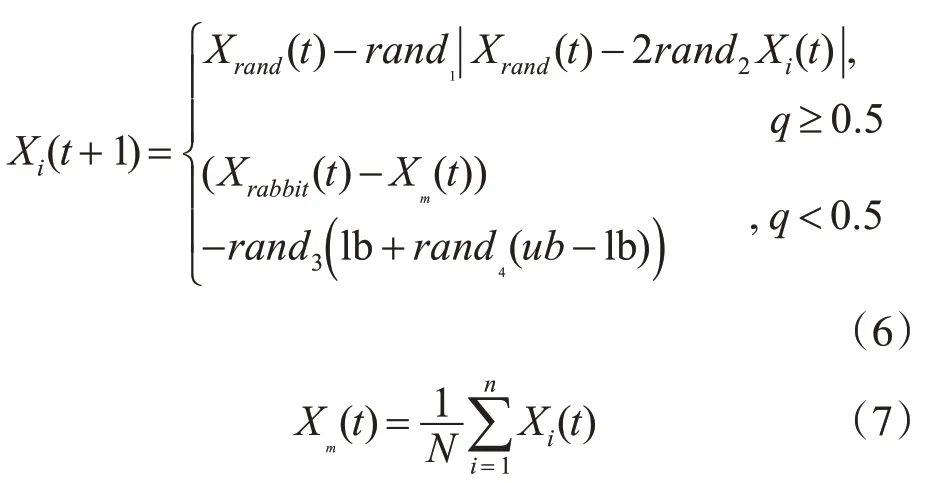
式中，Xi(t+1)和Xi(t)分别为第t+1代和t代种群中的第i个体的位置，Xrabbit是第t代为止所获得的全局最优位置，即目前的全局最优解，Xrand是第t代种群中随机选取获得的个体位置，Xm是当前种群所有个体的平均位置，q和randi（i=1，2，3，4）均是服从在（0，1）区间上的均匀分布的随机数，lb和ub分别是搜索空间的下界和上界。

2）从探索到开发的过渡阶段

HHO算法中，每代种群中的每一个个体都会依据猎物的逃逸能量E选择进入探索阶段或者开发阶段。逃逸能量E的公式如下所示：

式中，E0表示猎物初始的逃逸能量，是服从在（-1，1）区间上的均匀分布的随机数，t是当前迭代次数，T是最大迭代次数。

3）开发阶段

该阶段中，HHO算法模拟了鹰群的围捕行为，建模成四种不同的搜索策略，分别为软围攻，硬围攻，具有渐进式俯冲的软围攻以及具有渐进式俯冲的硬围攻。代种群中的每一个个体都会依据猎物的逃逸能量E以及服从在区间（0，1）上的均匀分布的随机数r的取值选择执行相应的捕食策略更新种群。上述搜索策略具体的数学表达形式为

（1）软围攻策略：当r≥0.5，||E≥0.5时，因为猎物的逃逸能量较高，具有足够的体力进行逃跑，所以鹰群选择包围猎物。该策略的数学公式如下：

式中，Jump是猎物的随机跳跃强度，表达式为Jump=2×(1-rand5)，rand5是服从在区间（0，1）上的均匀分布的随机数。

（2）硬围攻策略：当r≥0.5，||E＜0.5时，因为猎物的逃逸能量较低，所以鹰群使用较为强硬的包围策略。该策略的数学公式如下：

（3）具有渐进式俯冲的软围攻策略：当r＜0.5，||E≥0.5时，虽然猎物仍然有体力逃跑，但鹰群采取软围攻与尝试性的俯冲捕杀相结合的方式进行捕猎。该策略的数学公式如下：

式中，F是最小化问题的适应度函数值，S是一个大小为1×D，其中元素为服从在区间（0，1）上的均匀分布的随机数的向量，D为该最小化问题的维度，LF是大小为1×D，其中元素为服从levy分布的随机数的向量。levy分布的一维计算公式如下：

式中，μ和ν都是服从在区间（0，1）上的均匀分布的随机数，β一般取值为1.5。

4）具有渐进式俯冲的硬围攻策略：当r＜0.5，||E＜0.5时，猎物没有足够的体力逃跑，所以鹰群采取硬围攻与尝试性的俯冲捕杀相结合的方式进行捕猎。该策略的数学公式如下：

3 改进HHO算法

针对离散问题的求解需求，本文提出了一种新颖的改进HHO算法（Neighborhood Greedy Harris Hawks Optimization，NGHHO）。该算法主要是采用了随机实数编码方式、k-mean聚类方法、邻域搜索算子以及贪婪策略等方法以适应对于MTSP这类离散型问题的求解。

3.1 随机编码方式

随机编码是一种将离散空间中的一个组合转换成连续空间中的一组解的方法。该编码将一个实数分为两个部分，即整数部分和小数部分。整数部分的意义是旅行商的序号，小数部分表示了路径顺序。

小数部分的表示细节如下：对于MTSP问题来说，首先每个城市对应于一个实数，就产生了一个实数向量；然后根据该向量的小数部分进行升序排序，可以得到一个路径顺序，如图3所示，城市1到5分别对应着0.8到0.4，将其升序排列，就得到了每个城市所在的位置，即5-3-4-1-2，转化为路径就是4-5-2-3-1。

图3 随机编码

因为TSP问题中的路径信息是离散的一串数组，原始的HHO算法是一种在连续空间上求解的优化算法，所以本文采用该方法将TSP问题中的路径信息转化为一组实数解，再带入到HHO算法中进行求解。

3.2 k-mean聚类

在MTSP中，k-mean算法可以用于将城市群分配给K个旅行商，其主要思想是首先在城市坐标点集合中选取K个点，即聚类中心，然后计算每个点到所有聚类中心的欧式距离，将每个点分配给欧氏距离最近的那个聚类中心，得到一个个簇，最后通过不断迭代更新簇得到聚类结果。该方法产生的初始解质量较高。

3.3 邻域搜索算子

为了避免算法的过早收敛，本文采用了三种基础的邻域搜索算子［16］来提升算法鹅性能。这三种基础的邻域搜索算子分别是随机交换算子、随机插入算子和随机反转算子。

1）随机交换算子：在一次旅行中随机选择两座城市，然后交换两个选定城市的访问顺序。使用该算子的优点之一是使得每个城市之间有更多彼此相邻的可能性，对路径产生一定的干扰和变化。如图4（a）所示，随机交换算子使得城市2与城市5的位置被交换了。

2）随机插入算子：该算子随机选择两个城市，然后它将第i个城市提到第j个城市的后面进行访问。该算子相较于随机交换算子对路径的改变更小。如图4（b）所示，随机交换算子使得城市2插入到了城市3的位置。

3）随机反转算子：该算子随机选择一连串城市。然后它将第i个城市到第j个城市的顺序颠倒过来（即在路径组合中随机选择两个点，然后反转位于两个选定点之间的城市的顺序）。如图4（c）所示，随机交换算子使得城市1和城市5之间所有城市的位置发生了翻转。

本文中在鹰群在开发阶段和每次迭代的解集更新阶段后加入了邻域搜索算子。在开发阶段，为了增强HHO算法的局部搜索能力，所以结合鹰群围捕思想使用随机交换算子和随机翻转算子重新定义了软围攻和硬围攻策略。具体方法如下：按照原始HHO中，根据当前最优解的位置更新鹰的位置的围攻思想，将对当前迭代的最优解使用随机交换算子和随机翻转算子进行当前解的更新，定义为新的软围攻和硬围攻，其可以记为如式（18）和（19）。同时，传统的HHO容易陷入局部最优，为了增加种群的多样性，在每次迭代解集更新阶段后，所有使用上述三种邻域搜索算子对解进行一次变异。该变异具体方法如下：每只鹰按照等概率的可能会选择三种算子或者保持不变共四种策略进行一次变异移动。上述方法可以记为式（20）。

3.4 贪婪策略

采用三种邻域搜索算子以及HHO算法对问题进行求解的时候，由于缺乏问题本身的信息指导，其更新策略是偏向于随机的，解的迭代更新中容易产生冗余路径。为了使得HHO算法的搜索过程能够更加高效，使搜索结果能够不断趋近最优解。本文将HHO算法和贪心选择相结合，通过在HHO算法的俯冲阶段中采用贪婪策略［17］，使得算法的能力得到改善。由于TSP问题优化目标是距离因素，所以本文采用的贪婪策略基于距离因素，在HHO俯冲阶段，将原本的模拟俯冲定义为在路径组合中随机选择某一个城市后插入一个距离该城市最近的城市，产生一个新解，其可以表示为如下公式。

3.5 算法描述

本文所提出的NGHHO算法的伪代码和流程如算法1和图5所示。

图5 NGHHO算法流程图

4 实验结果与分析

实验使用Matlab R2018b编写了改进HHO算法。实验中将NGHHO与一些群体智能算法进行比较，对比算法包括粒子群算法（PSO）［13］，Harris鹰群优化算法（HHO）［15］以及灰狼优化算法（GWO）［18］。所有算法的搜索个体数1.5倍的城市数量，运行次数为30次，迭代最大代数为2000代。实验中的所有算法的参数设置如下：粒子群算法的局部学习因子为2，全局学习因子为2。本文进行了两种实验。

第一种实验是采用了solomon测试集中c101问题（http：//w.cba.neu.edu/～msolomon/problems.htm）为实验数据在长、宽、高分别为100、50、100的立方体表面上进行了实验。考虑不同问题规模，又分为30次100迭代30个点的2旅行商MTSP问题和30次2000次迭代100个点的4旅行商的MTSP问题，第一个30个点的实验结果如图6（a）和图7（a）所示，第二个100个点的实验结果如图6（b）和图7（b）所示。从图6（a）和6（b）示出NGHHO找到的最优路径，可见在不同规模下的MTSP问题中，NGHHO基本上可以找到一个可行解，而图7（a）和7（b）显示了各算法的平均收敛曲线，可见与HHO，GWO和PSO相比，其找到的解更优。通过以上分析可得，NGHHO在寻优精度以及跳出局部最优的能力上都比原始HHO，PSO和GWO强。

图6 测试集上NGHHO获得的最短路径

第二种实验是在20、30、40的立方体上，随机生成100个坐标（即这些坐标与第一种实验不同可以分布在立方体的任意面上）进行的实验。其同样进行两种规模的实验，30个点实验结果如图8（a），8（b）和7（c）所示，100个点的实验结果则显示于图8（c），8（d）和7（d）。从图8同样可以展示出在不同规模中NGHHO找到的最优路径，NGHHO基本上具有搜索到可行解的能力，从图7（c）和7（d）中可以看出算法随着迭代次数的增长所求得的总路径长度虽然下降增速有所减少但是仍然是不断降低的，同时也显示NGHHO与其他群智能算法相比，所求得总路程一直是较优的。通过上述分析NGHHO具有一定的优越性。

图7 实验结果

图8 随机点集上NGHHO获得的最短路径

5 结语

本文讨论了立方体表面上的MTSP问题上两点间的距离计算方法，并针对该问题的特征，使用k-mean聚类，邻域搜索和贪婪策略改进了Harris鹰优化算法，并利用改进后的算法有效地求解了该问题，得到了一种较为简单且有效的在任意立方体表面上的MTSP问题的求解方法。该方法适用于在任意大小的立方体上的路径规划问题，可以考虑应用于室内爬墙机器人的路径规划或者大厦外侧清洁路径规划等特殊几何表面的路径优化问题，具有一定的使用价值。