变截面二维功能梯度微梁的振动和屈曲特性*

雷 剑，谢宇阳，姚明格，何玉明

（1.华中科技大学 航空航天学院，武汉 430074；2.天津航天瑞莱科技有限公司，武汉 430056）

引言

功能梯度结构是近三十年发展起来的一种新型复合结构，其是由两种以上材料依据特定的设计原则，所形成的材料性能沿一定方向光滑变化的组织和结构.相比传统复合结构，功能梯度结构的显著特点是各组分间没有明显的界面，避免了因材料性能突变而造成的应力集中和层间破坏.目前，功能梯度材料在工程中得到了广泛应用，如土木工程、船舶和航空航天工程等.

建立功能梯度结构力学行为的理论模型并分析其内在规律是功能梯度结构的优化设计和工程应用的前提和基础.基于此，国内外诸多学者开展了相关研究工作.例如，Sina 等[1]建立了功能梯度梁自由振动的解析模型并分析了边界条件、体积分数等对固有频率和模态的影响.Alshorbagy 等[2]基于Euler-Bernoulli 梁理论和虚功原理建立了功能梯度梁的自由振动力学模型，并用有限元法得到了相关数值解.Şimşek[3]研究了移动质量块影响下功能梯度梁的振动特性.Aydogdu[4]采用半逆解法分析了轴向功能梯度梁的振动和屈曲行为.王伟斌等[5]建立了多孔功能梯度材料Timoshenko 梁的力学模型，并分析了其自由振动特性.蒲育等[6]基于改进型广义微分求积法研究了功能梯度梁的屈曲行为.马连生等[7]应用一阶剪切变形理论研究了FGM 梁的过屈曲行为.此外，葛仁余等[8]基于Euler-Bernoulli 梁理论，研究了轴向载荷下轴向功能梯度变截面梁的振动和屈曲问题.杜运兴等[9]基于物理中面的概念，研究了轴向力作用下材料性能沿厚度方向变化的变截面功能梯度Timoshenko 梁的振动特性.

随着材料科学、微电子技术和微加工技术的发展，各类微/纳米机电系统(MEMS/NEMS)相继出现并得到广泛应用，功能梯度结构的应用范围也被进一步拓展到了MEMS/NEMS 领域[10-11].微纳米结构的一个显著特点是其力学行为表现出明显的尺度效应[12-15].为描述微结构力学行为的尺度效应，包含额外材料尺度参数的非经典连续介质力学理论相继出现并得到了广泛的应用，如非局部弹性理论[16]、应变梯度弹性理论[13]和修正的偶应力理论[17]等.

近些年来，许多研究者针对微尺度功能梯度梁结构的力学性能开展了研究工作.Asghari 等[18]基于Euler-Bernoulli 梁理论和修正的偶应力理论分析了功能梯度微尺度梁的静态弯曲和自由振动尺度效应.Reddy[19]基于Euler-Bernoulli 和Timoshenko 梁理论建立了功能梯度微尺度梁静态弯曲、自由振动和屈曲力学模型，并分析了尺度参数、材料梯度指数等的影响.随后，Şimşek 和Reddy[20]基于统一的高阶剪切变形梁理论和修正的偶应力理论研究了功能梯度微尺度梁的弯曲和振动行为.考虑物理中面的影响，Al-Basyouni 和Tounsi 等[21]研究了功能梯度微尺度梁的弯曲和动态特性.Lei 等[22]基于应变梯度弹性理论和正弦剪切变形梁理论对功能梯度微梁的静动态力学特性和稳定性问题进行了研究.此外，Lei 等基于修正的偶应力理论和非局部热弹性理论分别研究了热环境下微米量级功能梯度梁的振动和屈曲特性[23]以及轴向功能梯度纳米梁的热屈曲行为[24].杨子豪等[25]基于新修正偶应力理论研究了平面正交各向异性功能梯度微梁的自由振动行为.Ebrahimi 等[26]建立了剪切变形功能梯度纳米曲梁的屈曲模型，模型中同时考虑了非局部效应和应变梯度效应的影响.

以上研究工作主要针对宏微观厚度方向和轴向功能梯度梁的力学性能开展，其材料性能沿一个方向连续变化.目前，材料性能沿单方向变化的一维功能梯度结构已无法完全满足工程结构在不同方向上的温度和应力分布要求，开展材料性能同时沿厚度和轴向变化的二维功能梯度结构力学性能的研究工作显得更为迫切和重要.例如，Lei 等[27]基于一新颖的高阶剪切变形理论研究了二维功能梯度梁的后屈曲行为，并分析了孔隙率的影响.Tang 等[28]研究了湿热环境下二维功能梯度梁的非线性振动特性.Barati 等[29]分析了磁场中二维功能梯度纳米梁的横向振动行为.Huang 等[30]研究得到了二维功能梯度Timoshenko 梁静态弯曲变形的精确解.

本文的主要目的是建立变截面二维功能梯度微尺度梁自由振动和稳定性问题的力学模型，研究梁的锥度比、功能梯度指数和轴向功能梯度指数、尺度效应等因素对其振动和屈曲行为的影响，以期为多维功能梯度结构的设计和优化提供理论支撑.

1 理论模型

1.1 变截面二维功能梯度微尺度梁

考虑如图1 所示的微尺度变截面二维功能梯度梁，长度为L，厚度和宽度随坐标x变化，分别记为h(x)和b(x)，其材料性能同时沿厚度方向和轴向连续变化.假定组分材料的体积分数符合幂律分布，根据混合律模型[31-32]，微梁的等效材料性能可以表示为

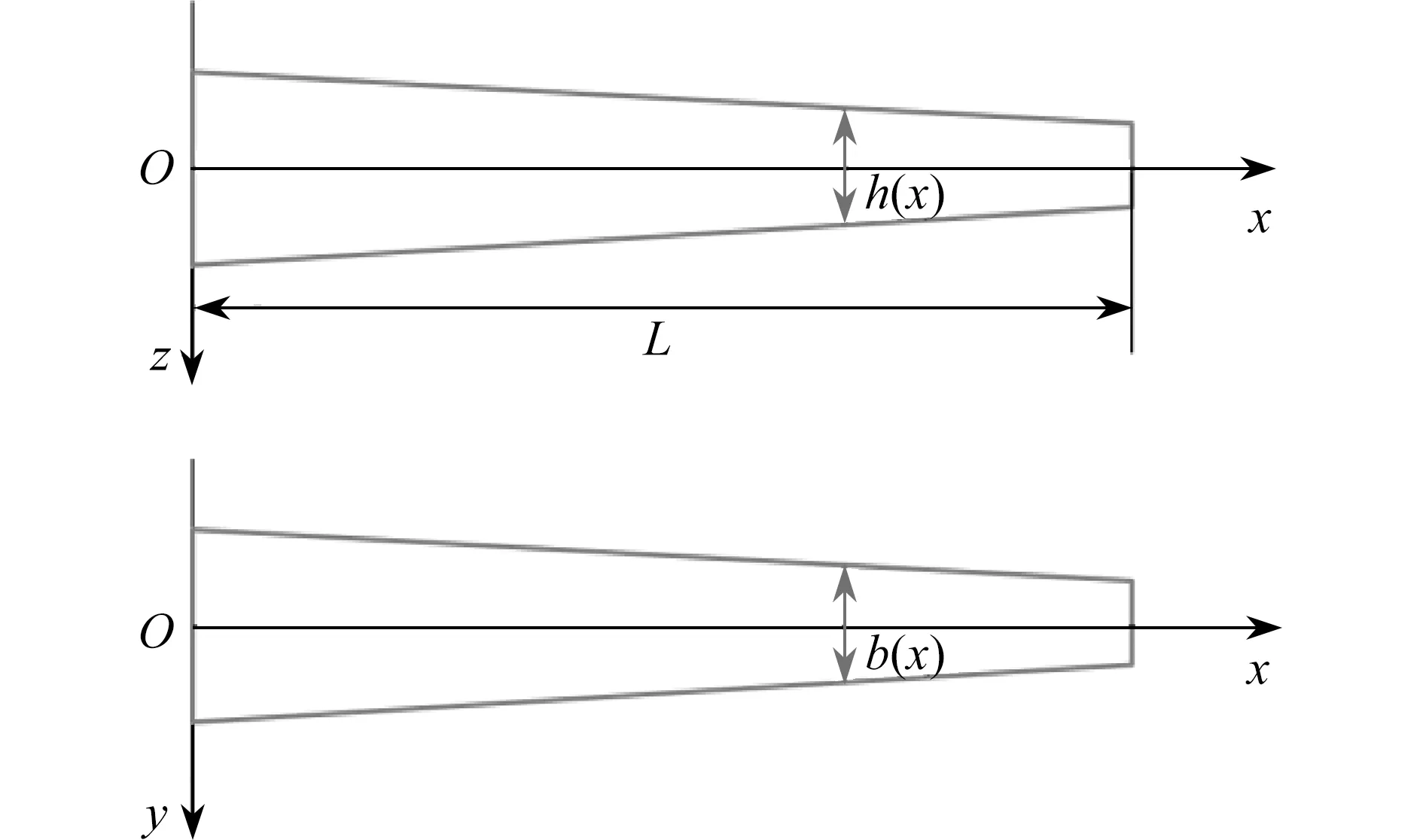
图1 二维变截面功能梯度微梁示意图Fig.1 Schematic diagram of a 2D variable-cross-section functionally graded microbeam

式中，Px和Pz为非负参数，分别表示轴向功能梯度指数和厚度方向功能梯度指数.下标“ c”和“ m”分别表示材料的陶瓷组分和金属组分.当Γ 分别为E，ν 和ρ时，可以得到微梁的等效弹性模量、等效Poisson 比和等效密度.

设定梁的厚度和宽度沿轴向线性变化，有

式中，hL和bL分别为微梁左端面的厚度和宽度，ch和cb（0≤ch＜1，0≤cb＜1）分别为微梁对应于厚度和宽度的锥度比.

1.2 振动和屈曲行为的控制方程

采用图1 中的直角坐标系，基于Timoshenko 梁理论，二维功能梯度变截面微尺度梁上任意一点的位移为

式中，u和w分别为微梁几何中面上一点的轴向和横向位移，φ 为微梁横截面绕y轴的转角.

传统应变张量的非零分量为

根据Hooke 定律，可得微梁的轴向正应力和横向剪应力为

式中，ks为 剪切修正系数.

Yang 等[17]发展的修正的偶应力理论含有一个与材料微结构有关的内禀特征尺度参数，可以预测微尺度构件力学行为的尺度效应.其本构关系中对称曲率张量 χij和偶应力张量的偏斜部分mij分别定义如下：

式中，l为材料内禀特征尺度参数，µ为剪切模量.

材料内禀特征尺度参数是微尺度材料的本征材料常数，已有研究者通过静态弯曲实验得出环氧树脂（epoxy）的尺度参数为17.6 µm[13].对于金属材料，已通过振动实验测得镍（Ni）、铜（Cu）和钛（Ti）的尺度参数分别为1.553 µm，1.422 µm 和0.775 µm[14-15].从以上研究中可以看出，不同材料的内禀特征尺度参数是有差异的，尤其是不同种类的材料.因此，对于由金属和陶瓷组成的二维功能梯度微尺度梁，根据以上分析，并参考文献[21,33]，我们假定其内禀特征尺度参数同样符合混合律.根据式（1），微梁的等效材料内秉特征尺度参数可以表示为

将式（5）代入式（7）中，可得对称旋转梯度张量的非零分量为

将式（10）代入式（8）中，可得偶应力张量的非零分量为

微梁在时间区间[t1,t2]上累积的应变能的一阶变分表达式为

式中，N，M，P和Q为各应力分量在微梁横截面上的合力，其表达式分别为

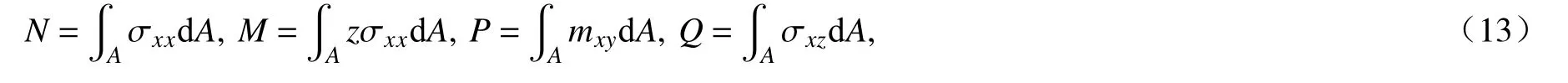
其中，A为微梁的横截面积，其大小为坐标x的函数，

微梁在时间区间[t1,t2]上累积的动能的一阶变分表达式为

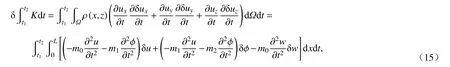
式中

轴向载荷Nx在时间区间[t1,t2]上所做的功的一阶变分为

微梁振动和屈曲行为的控制方程可由Hamilton 变分原理获得：

项目1：科研项目过程管理现状分析与体系构建，创新之处在于系统地进行国内外现状分析及构思信息化核算体系的搭建方案。

将式（12）、（15）和（17）代入式（18）中，可得微梁的运动方程为

微梁两端部（x=0和x=L）的边界条件为

将式（13）代入式（19）～（21）中，可得微梁位移形式的运动方程为

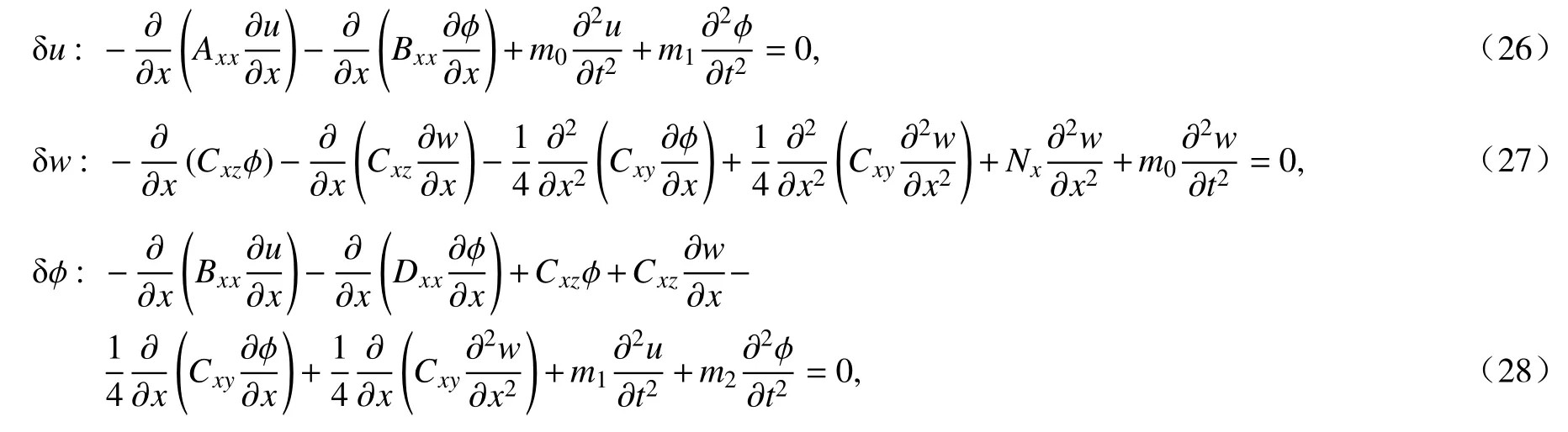
式中

同样地，微梁两端部（x=0和x=L）位移形式的边界条件为

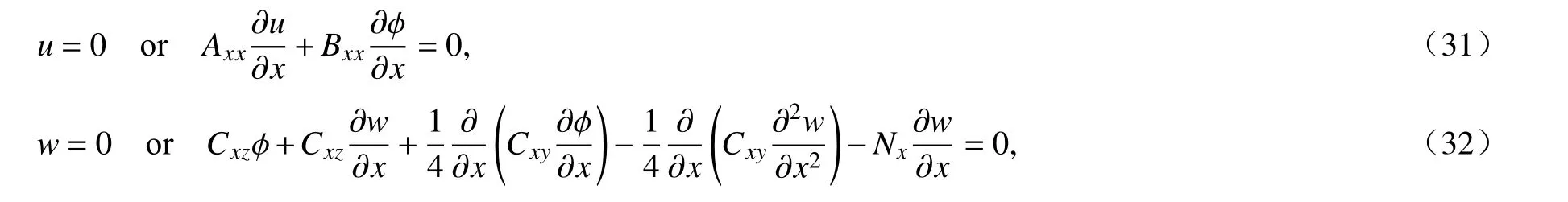
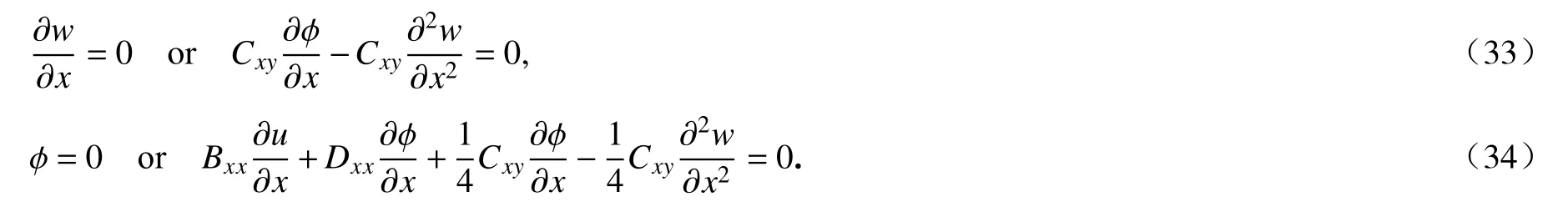
2 振动和屈曲问题的Ritz 解法

应用Ritz 法，可以获得任意边界条件下变截面二维功能梯度微梁振动和稳定性问题的数值解.

对微梁振动和屈曲控制方程进行加权积分，可得弱形式的控制方程，其等效于相应的运动方程和边界条件.根据式（26）～（28），变截面二维功能梯度微尺度梁弱形式的控制方程可由以下加权积分得到：

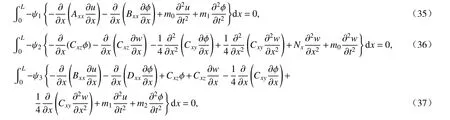
式中，ψ1，ψ2和 ψ3为权函数，分别满足u，w和φ 在端部的边界条件.

对式（35）～（37）进行分部积分，则变截面二维功能梯度微尺度梁弱形式的控制方程为

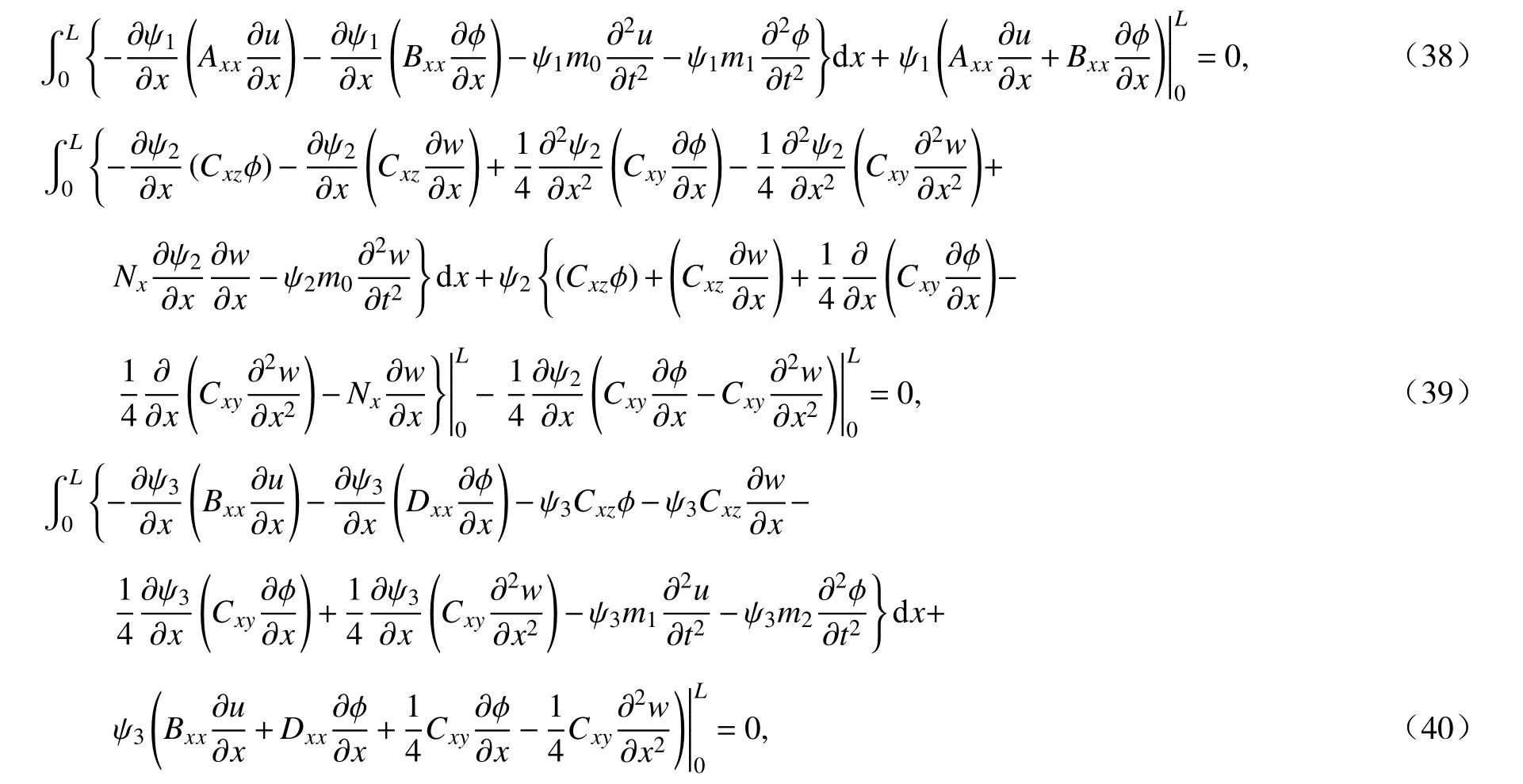
式中，域内积分部分为微梁的运动方程，边界积分为对应的运动边界条件.

将位移函数u，w和ϕ展开成以下形式：

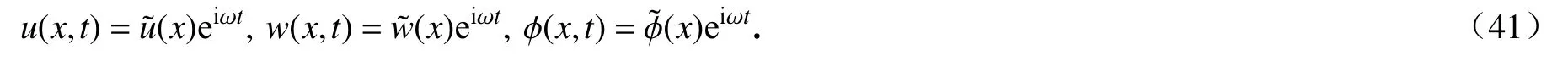
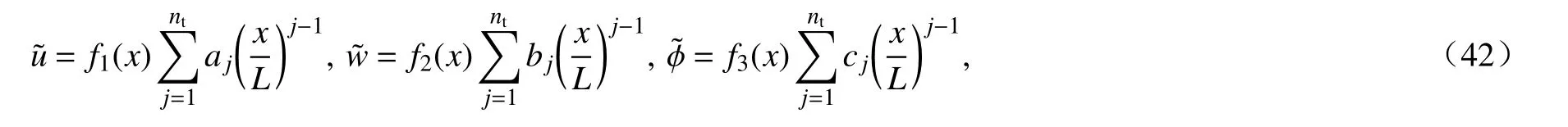
式中，aj，bj和cj为待定系数；f1(x)，f2(x)和f3(x)为满足边界条件的函数，定义如下：

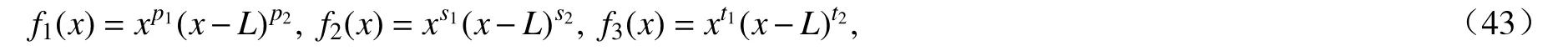
其中，指标p1，p2，s1，s2和t1，t2用于指定不同类型的边界条件，根据前述的位移限制条件，可得各指标的值，如表1 所示（表中C-C 表示两端固支，H-H 表示两端铰结，F-F 表示两端自由；C-H 表示左端固支右端铰结；HC 表示左端铰结右端固支；C-F 表示左端固支右端自由；F-C 表示左端自由右端固支，后同）.

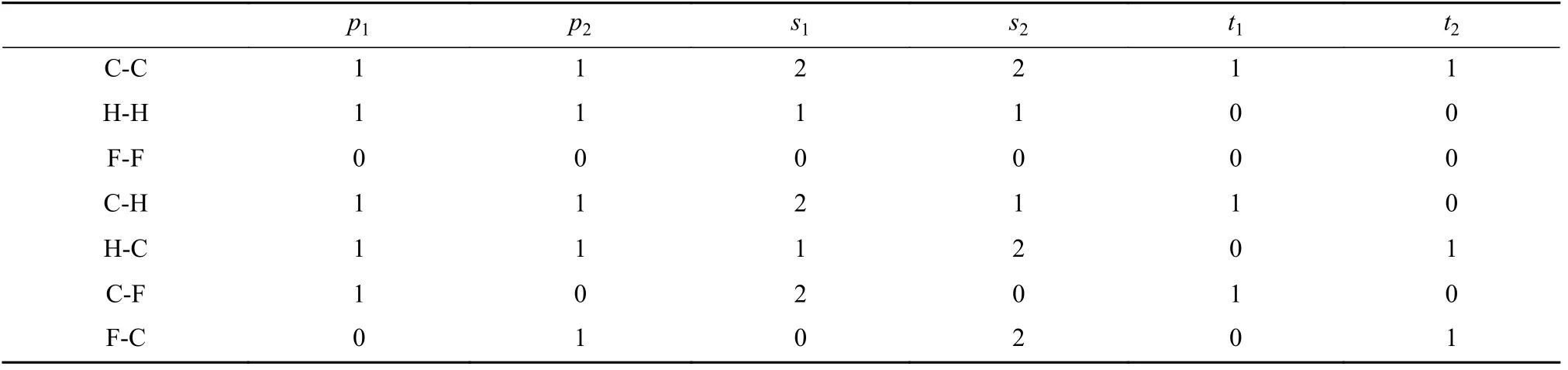
表1 不同边界条件时p1,p2,s1,s2 及t1,t2 的取值Table 1 Values of p1，p2，s1，s2 and t1，t2 with different boundary conditions

根据推导弱形式控制方程的相关原理，可令权函数 ψ1，ψ2和 ψ3分别等于边界函数f1(x)，f2(x)和f3(x).

将式（41）代入式（38）～（40）中，消去时间项，由控制方程的域内积分部分，可得到相应的特征值方程，对特征值方程进行求解，可得到微梁振动和屈曲问题的数值解.为了便于对比分析，引入以下无量纲参数：

3 算例分析与结果讨论

本节将给出基于Ritz 法的若干数值算例，详细分析尺度效应、锥度比、功能梯度指数等对变截面二维功能梯度微梁一阶固有频率和一阶临界屈曲载荷的影响.为便于表述，后续提到固有频率和屈曲载荷时均省略“一阶”.如无特别声明，设定功能梯度微梁由铝（Al：Em=70 GPa，ρm=2702 kg/m3，νm=0．3）和氧化铝（Al2O3：Ec=380 GPa，ρc=3960 kg/m3，νc=0．3）组成.假定微梁左端部的宽度等于左端部的厚度.此外，根据1.2 小节中的分析，金属组分Al 的内禀特征尺度参数取为lm=1．5 μm，因文献中没有关于陶瓷材料内禀特征尺度参数的相关实验数据，不妨设定陶瓷组分Al2O3的内禀特征尺度参数等于金属组分的内禀特征尺度参数（lc=lm=1．5 μm）.

3.1 结果验证

为验证当前力学模型的收敛性，表2 给出了nt逐渐增大时两端固支等截面二维功能梯度微梁的无量纲频率.从表中结果可以看出，随着nt的增加，计算结果迅速收敛，当nt取14 时，所得结果满足精度要求.此外，表3给出了宏观功能梯度等截面梁无量纲频率本文模型的计算结果与文献[34]中结果的对比，从中可以看出，两者吻合较好.表4 给出了宏观均质锥形梁无量纲频率本文模型的计算结果与文献[35]中基于Euler-Bernoulli 梁理论的结果对比，两者相吻合.以上分析表明，本文模型是准确可靠的.

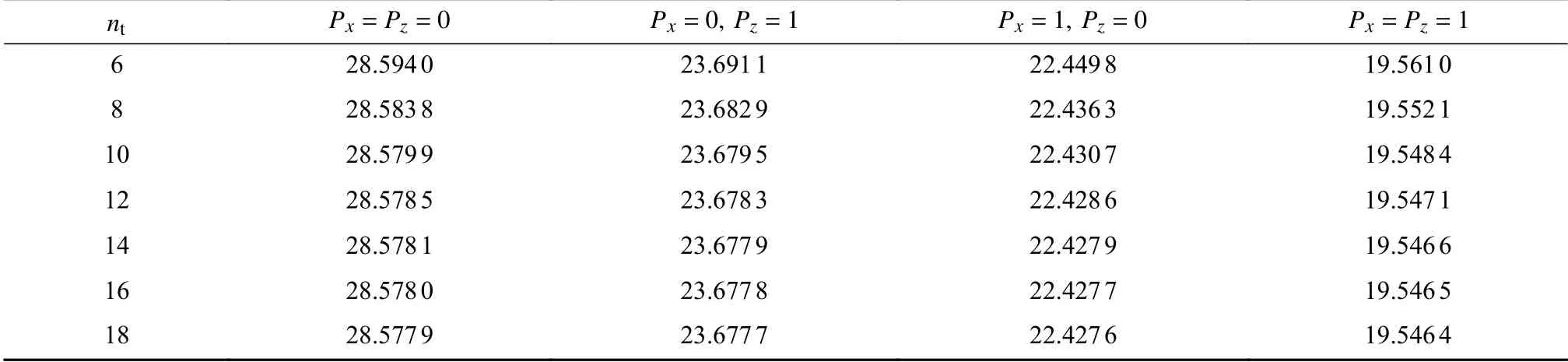
表2 二维功能梯度等截面微梁无量纲频率的收敛性分析（hL=1．5 μm，L=20hL，ch=cb=0，lc=lm=1．5 μm）Table 2 Convergence analysis of dimensionless frequencies of the 2D functionally graded equal-cross-section microbeam（hL=1．5 μm，L=20hL，ch=cb=0，lc=lm=1.5 μm）

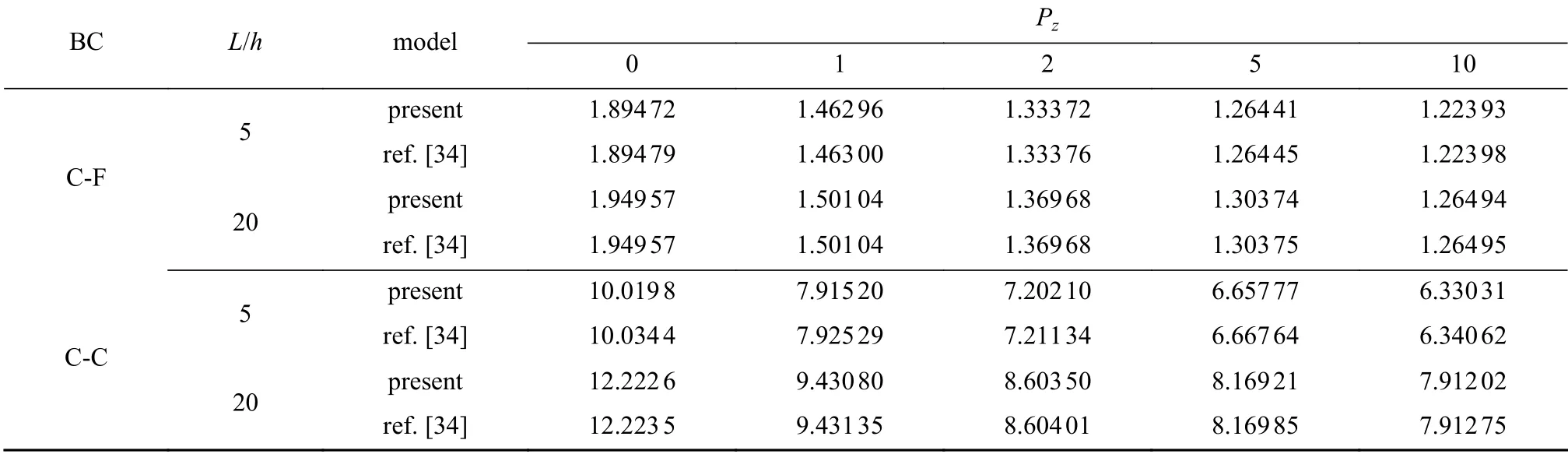
表3 基于本文模型的宏观功能梯度等截面梁无量纲频率与文献[34]中结果的对比（h=1 m）Table 3 Comparison of dimensionless frequencies of macro traditional equal-cross-section FG beams with ref.[34](h=1 m)

表4 基于本文模型的宏观均质锥形梁前三阶无量纲频率与文献[35]中结果的对比（C-F 边界，Pz=Px=0，此算例中Table 4 Comparison of the 1st 3 order dimensionless frequencies of macro traditional tapered beams with ref.[35](in this case：C-F boundary condition，

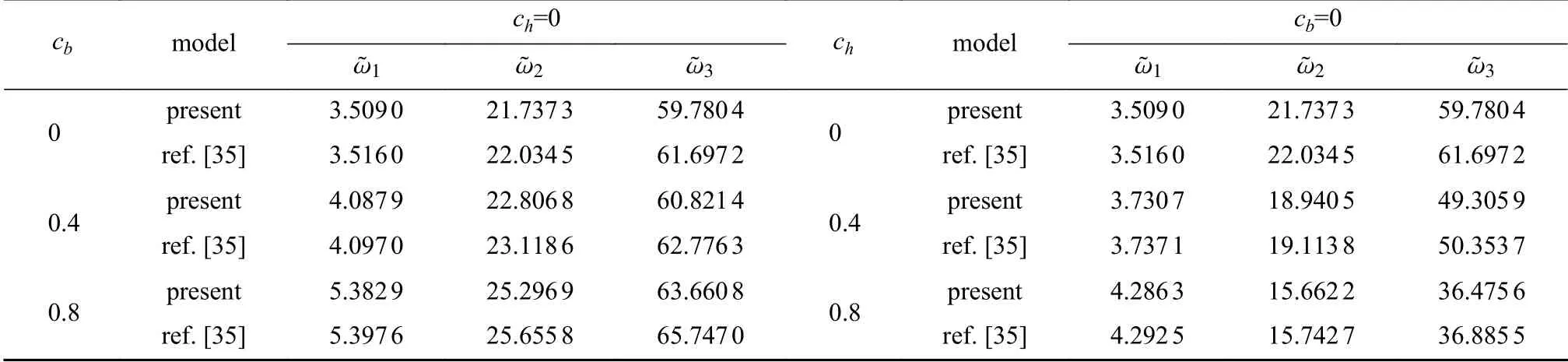
表4 基于本文模型的宏观均质锥形梁前三阶无量纲频率与文献[35]中结果的对比（C-F 边界，Pz=Px=0，此算例中Table 4 Comparison of the 1st 3 order dimensionless frequencies of macro traditional tapered beams with ref.[35](in this case：C-F boundary condition，

cbmodelch=0chmodelcb=0 ˜ω1˜ω2˜ω3˜ω1˜ω2˜ω3 0present3.509 021.737 359.780 40present3.509 021.737 359.780 4 ref.[35]3.516 022.034 561.697 2ref.[35]3.516 022.034 561.697 2 0.4present4.087 922.806 860.821 40.4present3.730 718.940 549.305 9 ref.[35]4.097 023.118 662.776 3ref.[35]3.737 119.113 850.353 7 0.8present5.382 925.296 963.660 80.8present4.286 315.662 236.475 6 ref.[35]5.397 625.655 865.747 0ref.[35]4.292 515.742 736.885 5

3.2 算例分析

图2～5 给出了不同边界条件下，微梁的无量纲频率随锥度比变化的情况.从图2 中可以看出，对于两端固支锥形微梁，无量纲频率随着锥度比ch的增大逐渐减小；对于锥度比cb，当其较小时（0≤cb≤0．6），无量纲频率变化不明显，当cb继续增大时，无量纲频率有较为明显的减小.在图3 中，两端铰支锥形微梁的无量纲频率随锥度比变化情况与两端固支时类似.从图4 可以看出，对于两端自由微梁，当锥度比ch增大时，无量纲频率先减小后增大；当锥度比cb增大时，无量纲频率在cb较小时缓慢增加，随后增长较快，这与两端固支和两端铰支边界时有明显差异.

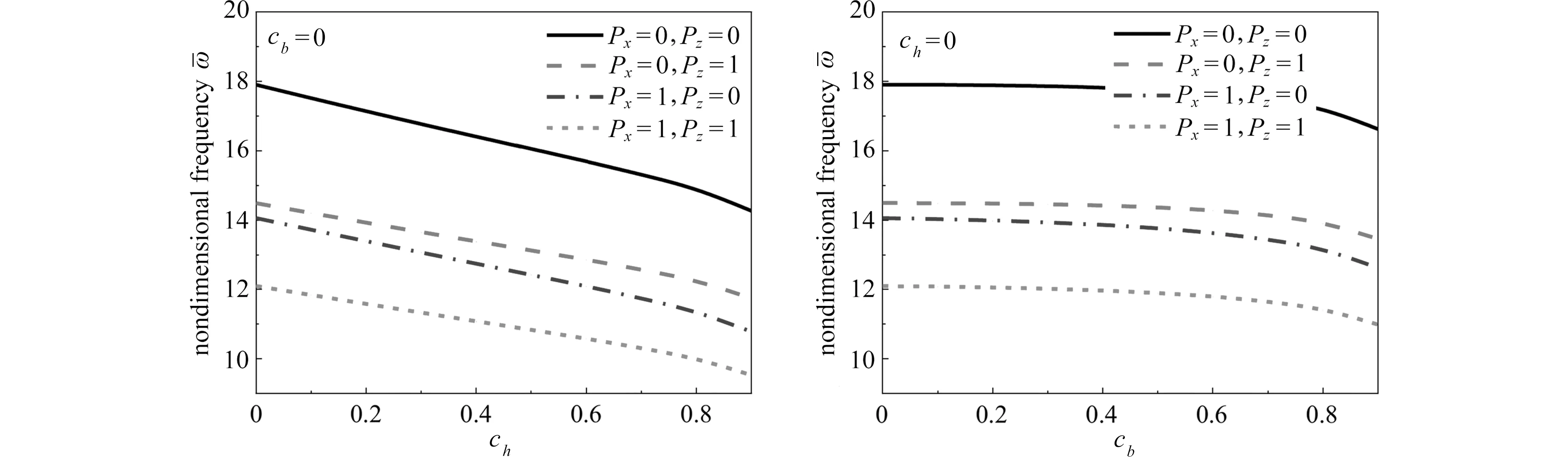
图2 两端固支边界时锥度比对微梁无量纲频率的影响（hL=3 μm，L=20hL，lc=lm=1．5 μm）Fig.2 The effects of taper ratios on the dimensionless frequencies of microbeams with clamped boundary conditions(hL=3 μm，L=20hL，lc=lm=1．5 μm)

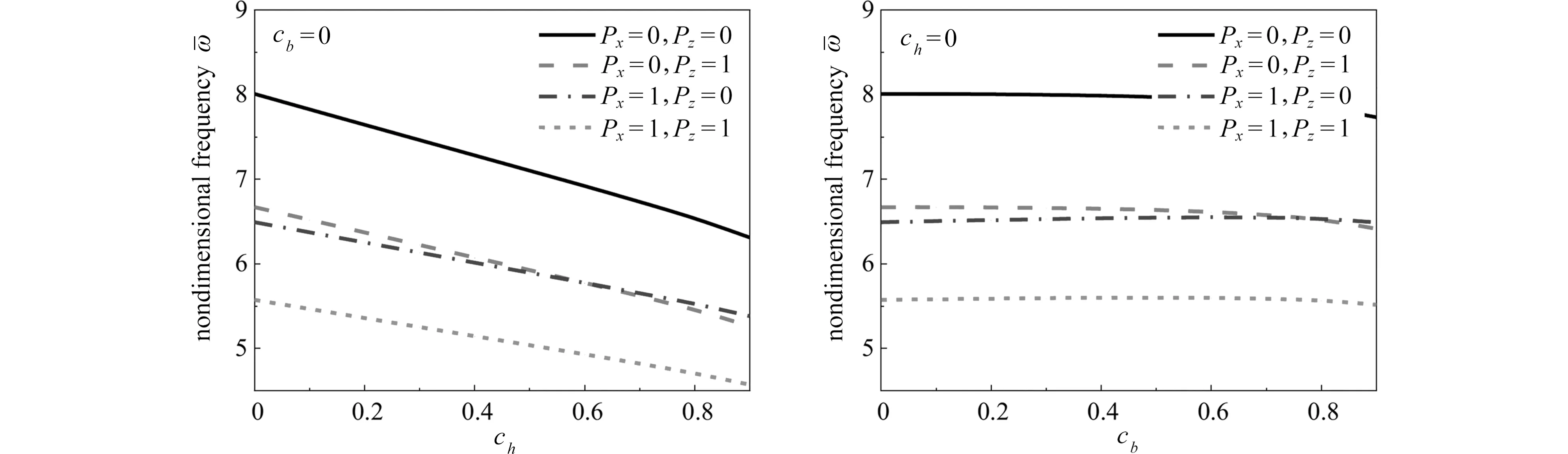
图3 两端铰支边界时锥度比对微梁无量纲频率的影响（hL=3 μm，L=20hL，lc=lm=1．5 μm）Fig.3 The effects of taper ratios on the dimensionless frequencies of microbeams with hinged boundary conditions(hL=3 μm，L=20hL，lc=lm=1．5 μm)

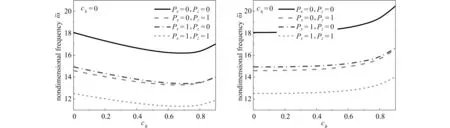
图4 两端自由边界时锥度比对微梁无量纲频率的影响（hL=3 μm，L=20hL，lc=lm=1．5 μm）Fig.4 The effects of taper ratios on the dimensionless frequencies of microbeams with free boundary conditions （hL=3 μm，L=20hL，lc=lm=1．5 μm）

图5 展示了左端固支右端自由（C-F）和左端自由右端固支（F-C）边界时锥形微梁的无量纲频率变化情况.结果表明，对于左端固支右端自由（C-F）微梁，其无量纲频率随着锥度比ch或cb的增大而增大；相反，对于左端自由右端固支（F-C）微梁，其无量纲频率随着锥度比ch或cb的 增大而减小.这说明，对于悬臂边界锥形微梁，固定端在锥顶（F-C）还是在锥底（C-F）对微梁无量纲频率有重要影响.

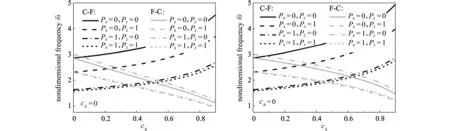
图5 悬臂边界时锥度比对微梁无量纲频率的影响（hL=3 μm，L=20hL，lc=lm=1．5 μm）Fig.5 The effects of taper ratios on the dimensionless frequencies of microbeams with cantilever boundary conditions(hL=3 μm，L=20hL，lc=lm=1．5 μm)

为探究微梁组分材料的轴向梯度分布和微梁轴向变截面效应对其无量纲频率的影响异同，图6～8 分别给出了仅考虑材料轴向梯度分布、厚度方向锥度比（ch）和宽度方向锥度比（cb）时，微梁的无量纲频率变化情况.从图6 可以看出，当轴向功能梯度指数较小时（Px＜ 5），微梁无量纲频率随着Px的增大迅速降低，随后趋于平缓，这是因为，轴向功能梯度指数在0～5 范围内变化时，微梁轴向的材料分布改变明显，对微梁频率的影响显著.从图7 和图8 中可以看出，锥度比（ch，cb）对微梁频率的影响与微梁的边界条件相关，相关影响规律在图2～5 中已进行了详细描述.此外，厚度方向锥度比（ch）的影响还与微梁的尺度效应相关，从图7 中可知，当考虑微梁的尺度效应时，ch对微梁无量纲频率的影响减弱.综合以上分析可知，三个因素均对微梁的无量纲频率有显著影响，而影响效果则存在较大差异，微梁的无量纲频率变化规律是微梁的材料分布、变截面效应、尺度效应和边界条件等因素综合作用的结果.

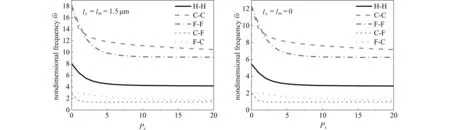
图6 轴向功能梯度指数对微梁无量纲频率的影响（hL=3 μm，L=20hL，ch=cb=0，Pz=0）Fig.6 The effects of axial functional gradient indexes on the dimensional frequencies of microbeams （hL=3 μm，L=20hL，ch=cb=0，Pz=0）

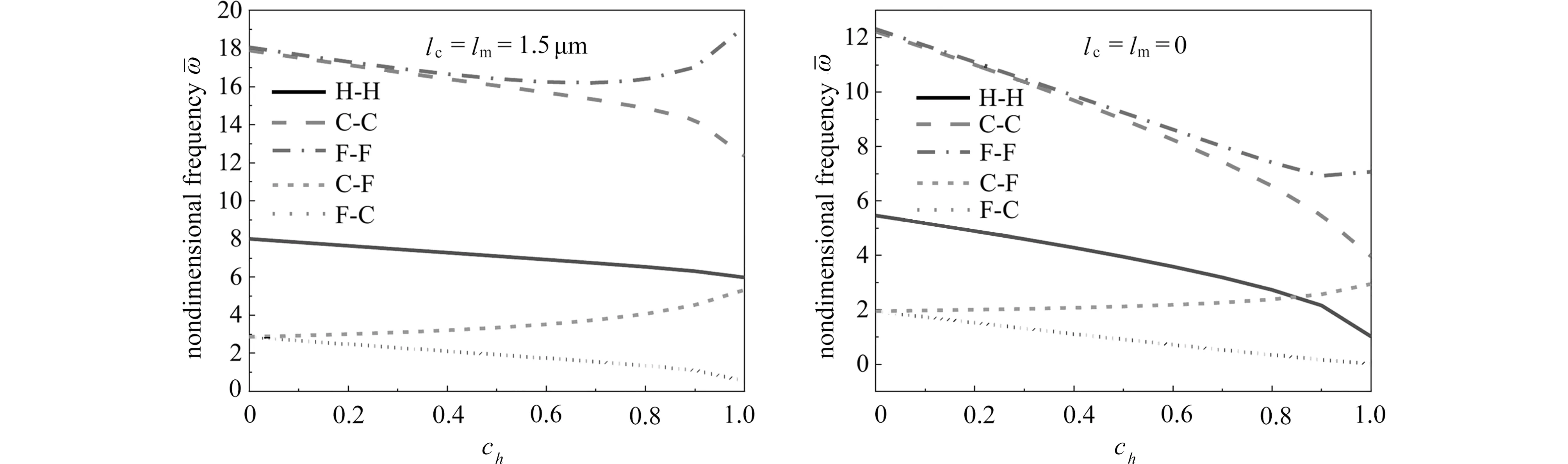
图7 锥度比（ch）对微梁无量纲频率的影响（hL=3 μm，L=20hL，cb=0，Px=Pz=0）Fig.7 The effects of taper ratios（ch）on the dimensional frequencies of microbeams （hL=3 μm，L=20hL，cb=0，Px=Pz=0）

图8 锥度比（cb）对微梁无量纲频率的影响（hL=3 μm，L=20hL，ch=0，Px=Pz=0）Fig.8 The effects of taper ratios（cb）on the dimensional frequencies of microbeams （hL=3 μm，L=20hL，ch=0，Px=Pz=0）

前述分析表明，自由边界时，频率随厚度方向锥度比（ch）变化时存在极小值点，这与其他边界条件时单调变化不同（图4 和图7）.为深入探究自由边界时微梁频率随锥度比（ch）的变化规律，图9 给出了自由边界时有无尺度效应、不同功能梯度指数下的频率变化情况.图中结果表明不论是否考虑尺度效应，频率随着ch的变化均出现极小值点，区别在于不考虑尺度效应时，极小值点出现在锥度比很大时（约0.95），考虑尺度效应时极小值点位置的ch约为0.7.此外，图中结果还说明，功能梯度指数的变化对极值点位置没有明显的影响.综合以上分析可知，频率极值点存在与否与梁是否有外界约束相关，尺度效应则会改变自由边界下频率极值点出现的锥度比（ch）.

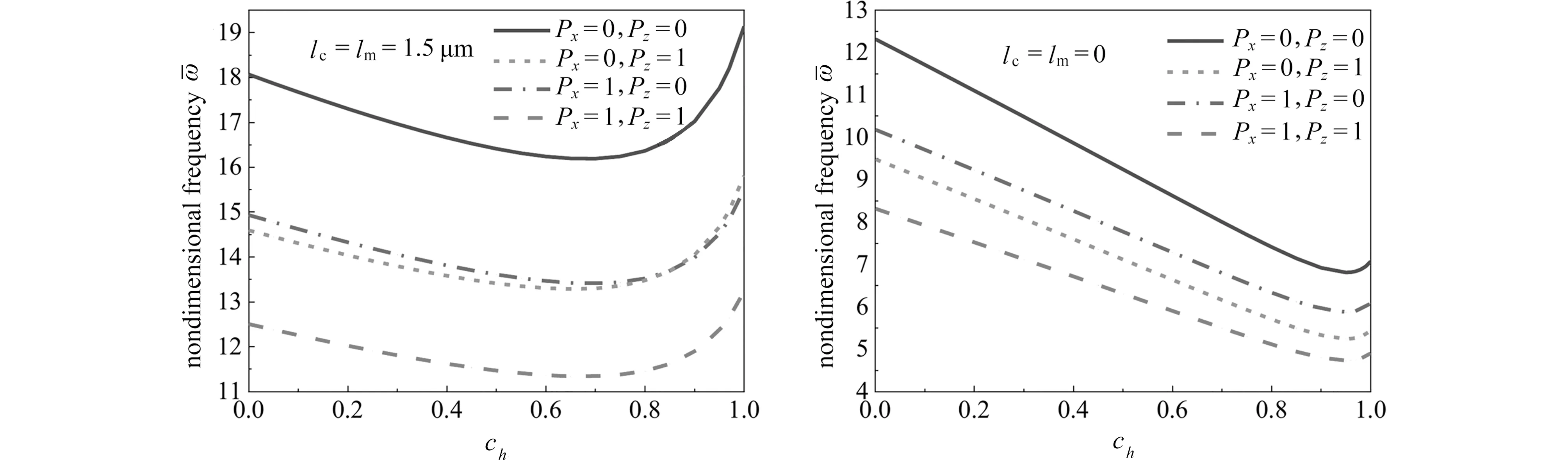
图9 锥度比（ch）对自由边界条件微梁无量纲频率的影响（hL=3 μm，L=20hL，cb=0，F-F）Fig.9 The effects of taper ratios（ch）on the dimensional frequencies of microbeams with free boundary conditions （hL=3 μm，L=20hL，cb=0，F-F）

图10 绘制了不同厚度下微梁的无量纲频率随梁的长厚比变化的曲线.结果表明，当微梁为厚梁时（L/h＜10），其无量纲频率随着长厚比减小而逐渐减小，当微梁长厚比大于10 时，微梁的无量纲频率变化趋于平缓.这说明当梁的长厚比较小时，剪切变形效应明显，梁的无量纲刚度明显降低，无量纲频率降低.此外，当微梁厚度逐渐增大时，无量纲频率减小，说明随着厚度的增加，小尺度效应逐渐降低.图11 绘制了陶瓷-金属的内禀特征尺度参数比变化时，无量纲频率的变化情况.图中结果表明，总体上来看，随着陶瓷-金属的特征尺度参数比逐渐增大，微梁的无量纲频率随之增大；但是微梁的边界条件不同时，各曲线的斜率不同，表明边界条件不同时，微梁尺度效应的影响不同.

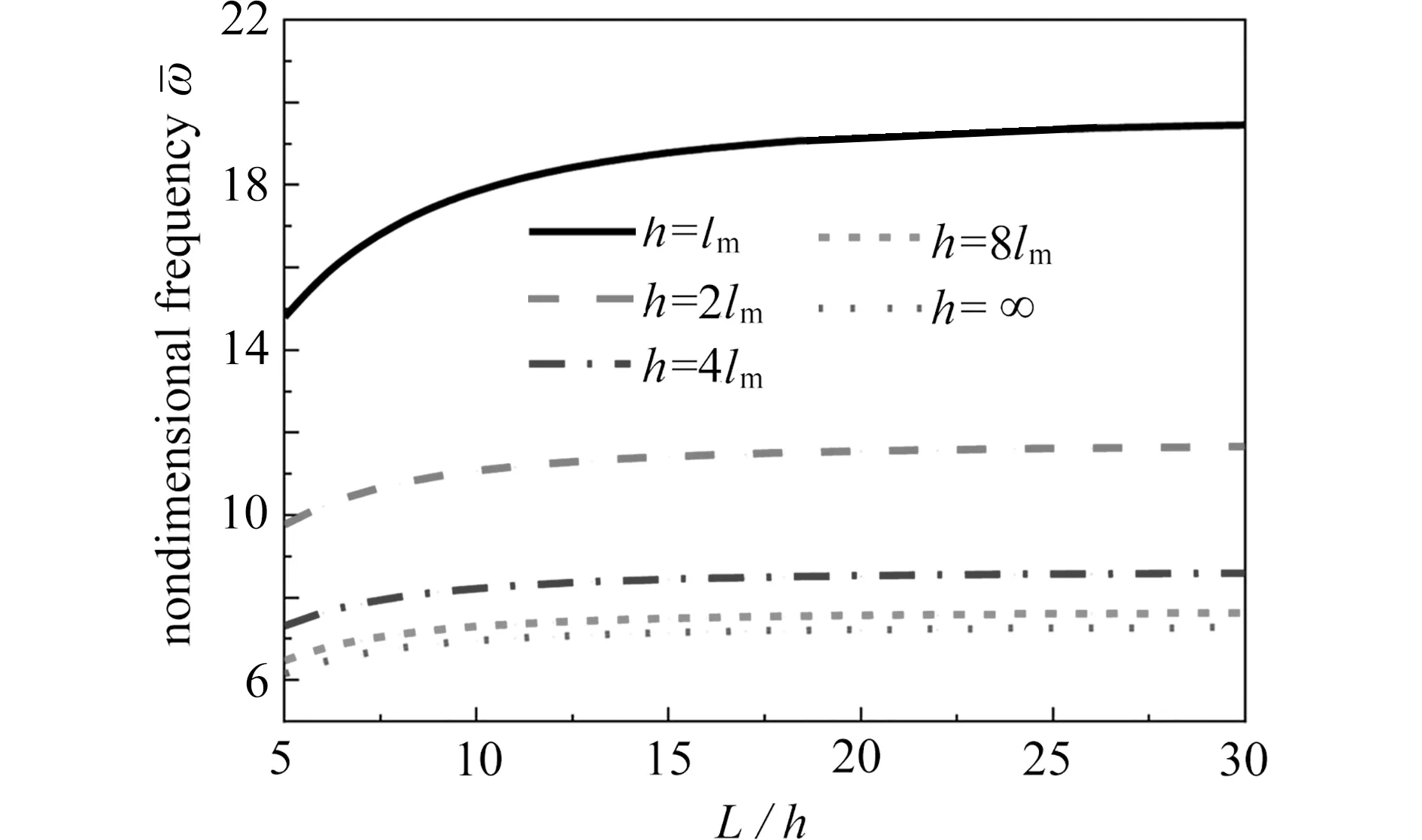
图10 长厚比对微梁无量纲频率的影响（C-C，ch=cb=0．2，Px=Pz=1，lc=lm=1．5 μm）Fig.10 The effects of length-to-thickness ratios on the dimensionless frequencies of microbeams(C-C,ch=cb=0．2,Px=Pz=1,lc=lm=1．5 μm)

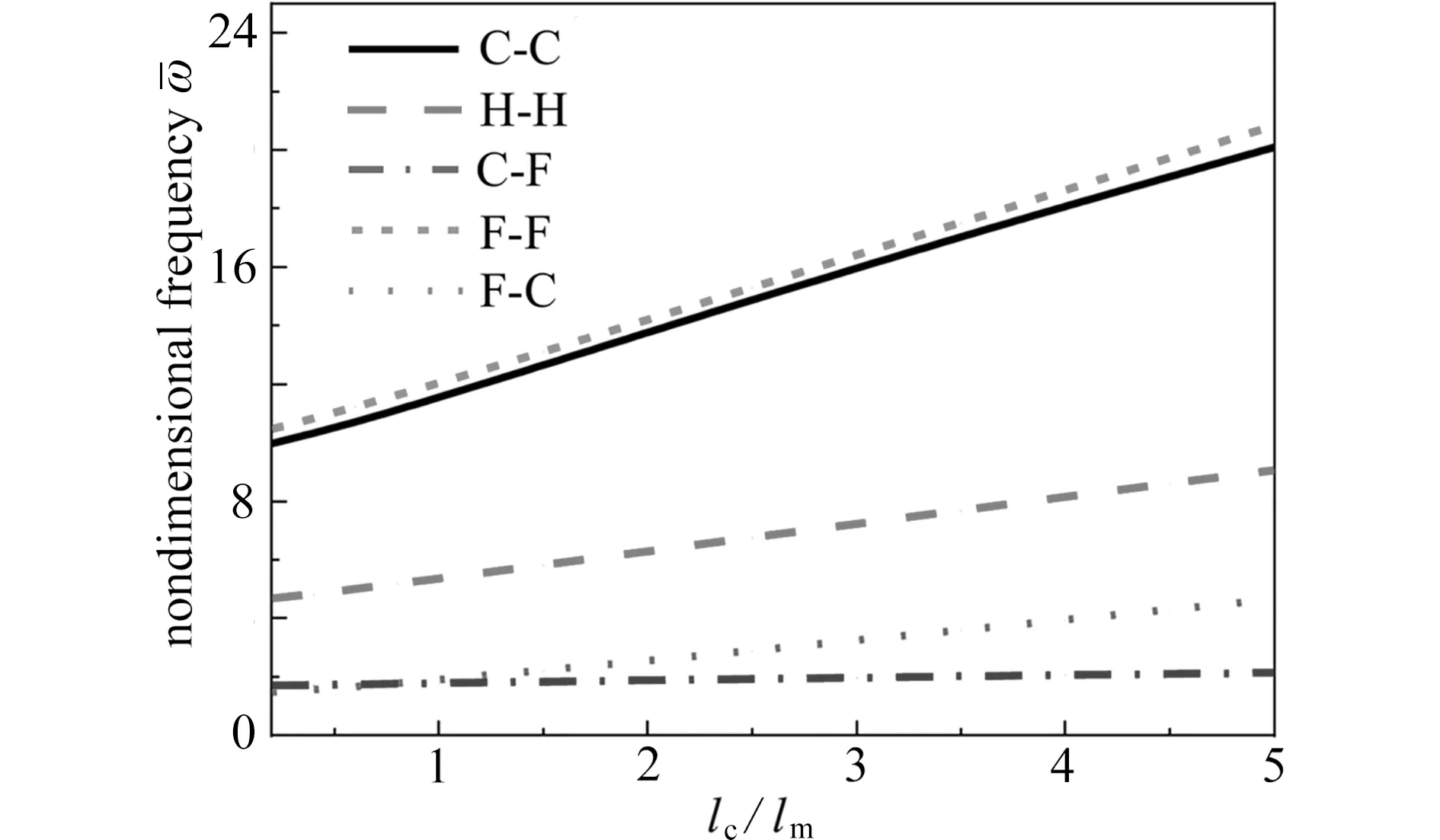
图11 陶瓷和金属的材料尺度参数比对微梁无量纲频率的影响（hL=3 μm，L=20hL，Px=Pz=1， ch=cb=0．2，lm=1．5 μm）Fig.11 The effects of the length scale parameter ratios of ceramic and metal on the dimensionless frequencies of microbeams(hL=3 μm，L=20hL，Px=Pz=1，ch=cb=0．2，lm=1．5 μm)

图12 给出了不同厚度下微梁的无量纲临界屈曲载荷随着功能梯度指数和轴向功能梯度指数变化的情况.结果表明，随着功能梯度指数或轴向功能梯度指数的增大，微梁的无量纲临界屈曲载荷逐渐减小；随着微梁厚度的增大，无量纲临界屈曲载荷同样随之减小.

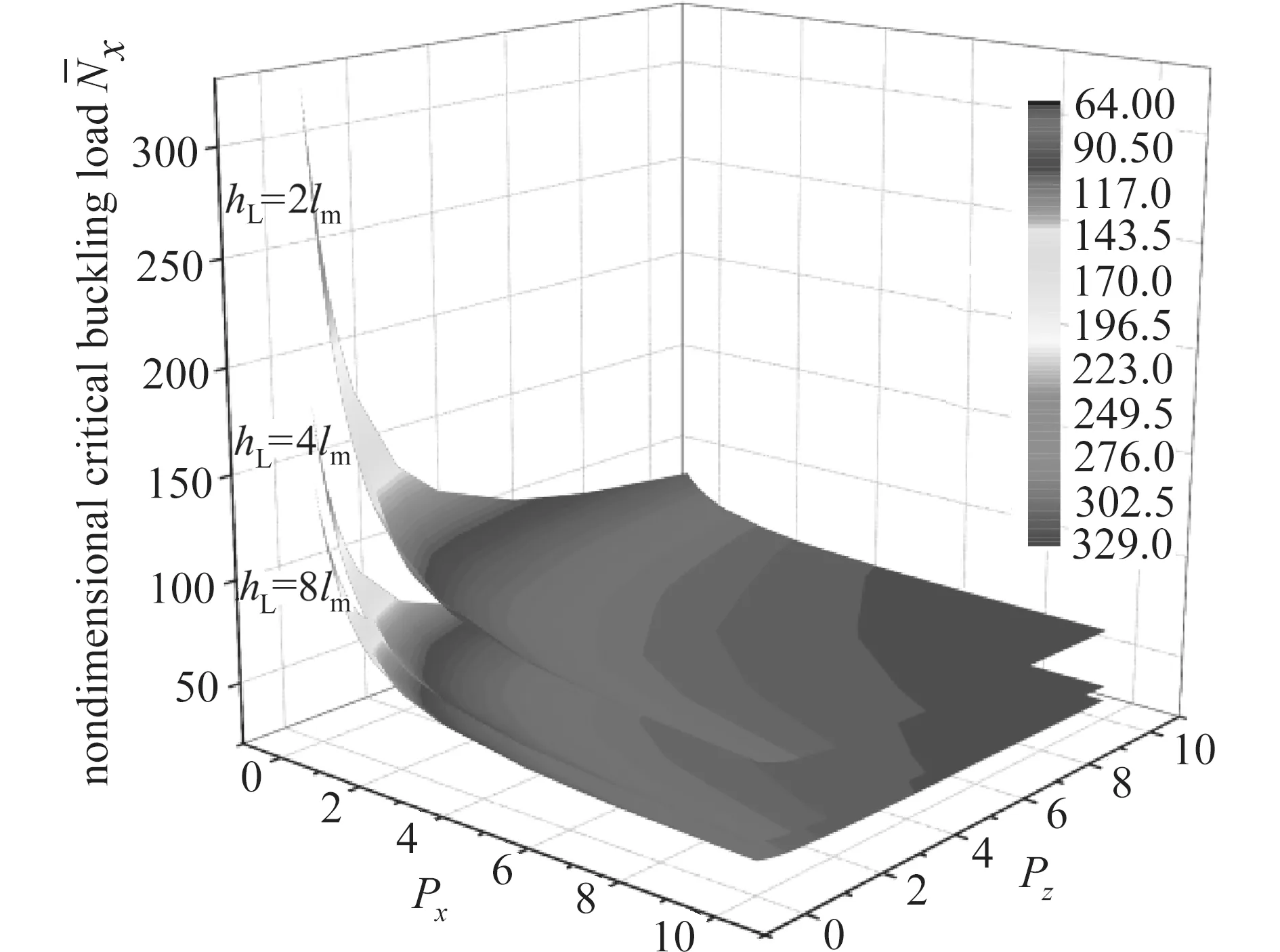
图12 两端固支（C-C）微梁的临界屈曲载荷随功能梯度指数和轴向功能梯度指数的变化情况（L=20hL，lc=lm=1．5 μm，ch=cb=0．2）Fig.12 The effects of the functionally graded indexes on the critical buckling loads of microbeams （L=20hL，lc=lm=1．5 μm，ch=cb=0．2）

4 结论

本文基于修正的偶应力理论和Timoshenko 梁理论，应用变分原理建立了变截面二维功能梯度微尺度梁自由振动和稳定性问题的力学模型.采用Ritz 法给出了任意边界下振动基频和临界屈曲载荷的数值解.通过若干数值算例探究了材料内禀特征尺度参数、锥度比、功能梯度指数和轴向功能梯度指数等对微梁振动和屈曲行为的影响，本文主要结论可以总结为：

1）自由边界时，频率随厚度方向锥度比（ch）变化时存在极小值点，在其他边界条件下，频率随ch的 改变单调变化.

2）长厚比较小时，剪切变形效应明显，微梁的无量纲频率降低；微梁厚度逐渐减小时，尺度效应增强，无量纲频率逐渐增加.

3）微梁的无量纲频率随着陶瓷和金属的材料内禀特征尺度参数比（lc/lm）增大而增大，且不同边界条件时，增大的程度不同，这也表明，不同边界条件时，尺度效应对微梁的影响程度不同.

4）微梁的无量纲临界屈曲载荷随着微梁厚度的增大而减小，随着轴向功能梯度指数或厚度方向功能梯度指数的增大而减小.