基于重构边界光滑离散剪切间隙法的复合材料层合板自由振动分析*
李 情,陈莘莘
(华东交通大学 土木建筑学院,南昌 330013)
引言
复合材料层合结构因其比强度高、耐高温耐腐蚀、比模量高、可设计性好等优点,广泛用于航空航天、汽车、船舶海洋等工程领域,对其振动特性的研究具有重要的工程意义[1-3].现有层合板理论的主要差别是对于横向剪切形变的处理,经典层合理论基于Kirchhoff-Love 假设,忽略了层间的剪切和挤压,只适用于薄板;一阶剪切变形理论(FSDT)考虑横向剪切形变,引入了剪切修正系数,对中厚板适用结果良好;高阶剪切变形板理论(HSDT)引入剪切应力沿板厚方向的非线性变化,避免了FSDT 剪切修正系数的引入,但是需要有限元方程C1连续,在实际计算过程中较难实现.诸多学者利用较为简洁的FSDT 对层合板进行了自由振动分析,得到了令人满意的结果.
迄今为止,工程结构分析中常见的数值计算方法有:有限元法、边界元法、无网格法等.作为应用最为广泛和成熟的数值计算方法,有限元法在复合材料层合板的动力问题分析中应用广泛[4-5].然而,传统的有限元法大多是基于自然坐标的,计算时需要进行等参变换和Jacobi 矩阵的计算,当单元严重不规则或变形时,坐标转换的要求将显著降低计算精度;同时,刚度矩阵存在过刚现象,对三角形单元等低阶单元尤为突出.为了解决上述难点,学者们提出了不同的解决方法,Liu 等[6]将有限元法和无网格法中的应变光滑技术相结合,提出了光滑有限元法(S-FEM),展现了良好的计算精度、效率和稳定性.基于光滑域构造方式的不同,光滑有限元法包括基于单元子域的光滑有限元法(CS-FEM)[6]、基于单元节点的光滑有限元法(NS-FEM)[7]、基于单元边界的光滑有限元法(ES-FEM)[8]和基于单元面的光滑有限元法(FS-FEM)[9].众多学者将光滑有限元法拓展到弹塑性问题[10-11]、板壳问题[12-13]以及复合材料分析[14-15]等领域,并取得了良好的结果.目前Reissner-Mindlin 板壳单元依然是工程实际数值计算中常见的单元类型,但当板壳厚度很薄时,常伴随“剪切自锁”的现象.为了消除自锁,众多学者开展了大量的研究工作,提出了不同的解决方法,比如基于选择性积分的板壳单元、MITC4 单元、C0 单元、EAS 单元、ANS 单元等.Bletzinger 等[16]提出了离散剪切间隙(DSG)法,构造了DSG3 单元,利用离散单元剪切间隙得到新的剪切应变矩阵,削弱了“自锁”现象.然而,原始DSG 单元的剪切应变会受单元节点编号的顺序变化的影响,尤其是对于不规则网格和畸变网格,计算精度和稳定性不高.
Nguyen-Xuan 和Nguyen-Thoi 等将光滑有限元法与DSG 法结合,提出了ES-DSG3 单元[17]、NS-DSG 单元[18]、CS-DSG 单元[12],用于分析Reissner-Mindlin 板的问题,得到了较好的结果.值得注意的是,在上述方法中虽然对应变矩阵进行了光滑处理,但是Reissner-Mindlin 板有限元方程中的荷载矢量、质量矩阵仍需要进行等参变换,无法完全避免坐标映射和变换.由此,Yang 等[19]基于全局坐标构造了Reissner-Mindlin 板改进的边界光滑DSG 单元(RES-DSG3),提出了一种非等参DSG 方法,将其与符号积分和光滑技术相结合,对矩阵进行了光滑处理,同时避免了坐标映射,并将此法用于分析Reissner-Mindlin 板,取得了良好的计算结果.本文借助于RES-DSG3 法,详细推导了复合材料层合板自由振动的控制方程,并编制了相应的MATLAB 程序,通过典型算例的计算,验证了本文方法的可行性和有效性.
1 层合板自由振动的有限元控制方程
基于FSDT,复合材料层合板的位移场可以描述为

式中,u,v,w表示层合板内任意点x,y,z变形后的位移,u0,v0,w0表示层合板中面上相应点的位移,βx,βy为中面法线关于y轴和x轴方向的转角,如图1 所示.
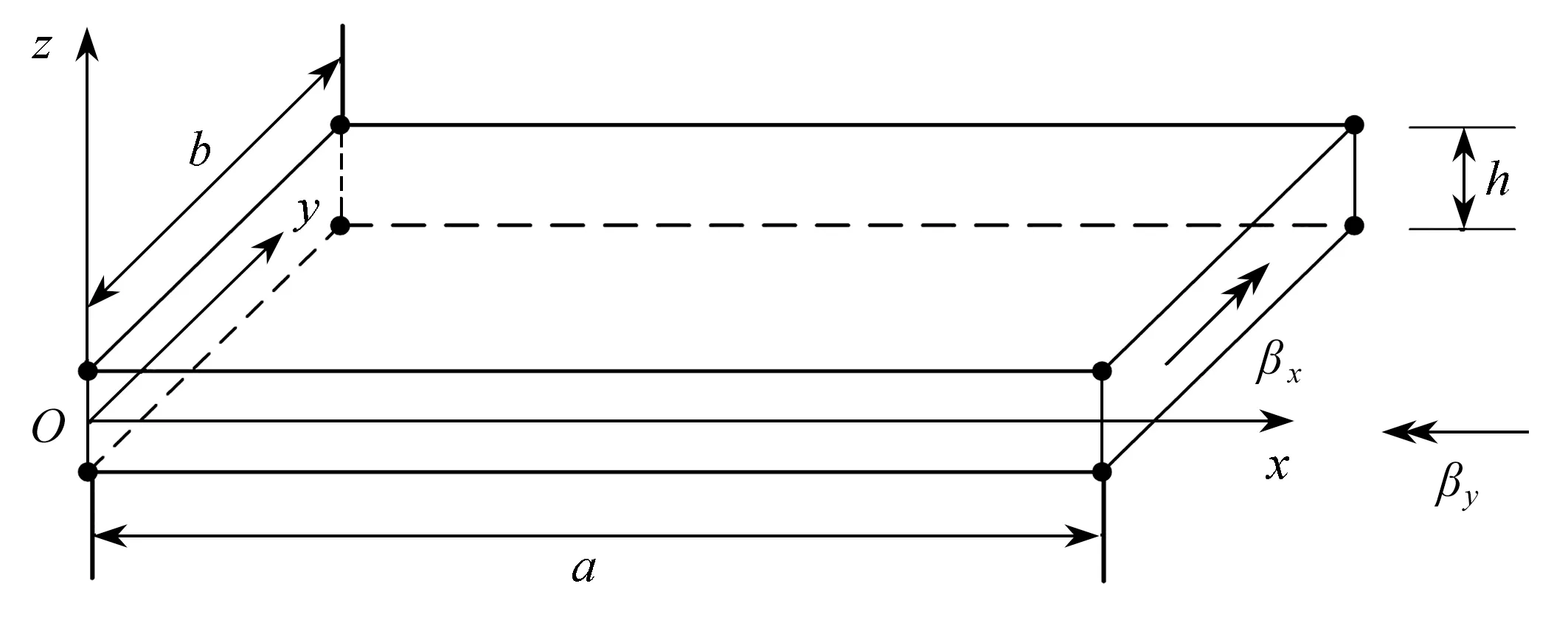
图1 层合板的坐标系Fig.1 The coordinate system for the laminate
位移应变关系为


合力、合力矩和等效剪力向量可分别描述为

则广义本构关系为

式中,A为拉伸刚度矩阵,B为耦合刚度矩阵,D为弯曲刚度矩阵,As为剪切刚度矩阵,它们的元素可以分别表示为

其中
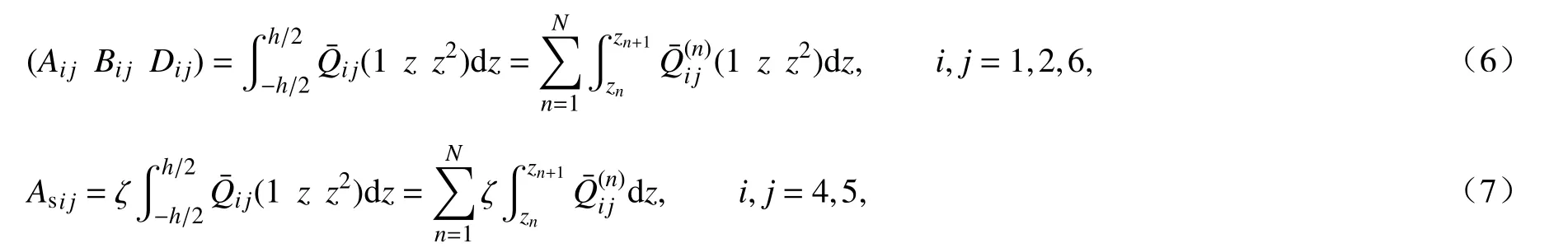
上标(n)表示第n层,表示弹性矩阵系数,ζ 为剪切修正因子.
根据Hamiltion 原理,不考虑阻尼,可得层合板自由振动的有限元控制方程为

式中,K为结构的系统刚度矩阵,M为结构的系统质量矩阵,u为系统的位移矢量.同时有

且



式中,Ni为单元的形函数.
单元的质量矩阵为

式中,m为质量密度矩阵,其表达式为

对第K层材料有

2 RES-DSG3 法[17]
2.1 基于全局坐标系的非等参DSG3 法
有限元方程中节点i相关的剪切间隙可描述为全局卡氏坐标系下的标量形式:

同时

全局坐标系下,三角形单元的形函数为

式中,xi,yi为三角形单元节点的全局坐标,aij(i=1,2,3;j=1,2,3)是与式(21)中逆矩阵对应的矩阵元素.
将形函数代入方程(17)、(18),得到

式中
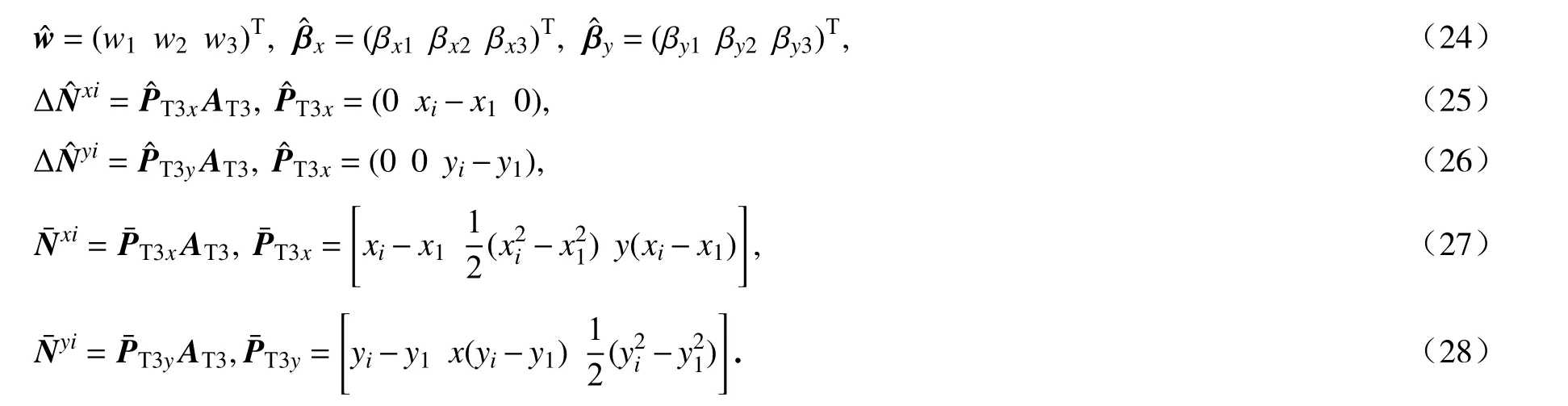
则剪切应变可表示为

基于DSG 方程,复合材料层合板的单元剪切应变可写为矩阵形式,如下:

式中

2.2 边界光滑技术
对于平面问题,基于符号积分和Gauss 散度定理有

式中,Г为积分域边界.
假设积分域包含k条边界,且为光滑连续,则式(37)、(38)可写为沿积分域边界的线积分之和:

应用近似积分技术,光滑域内点xC处的任意函数可表示为

式中,ϕ(x-xC)为光滑函数,定义为

将式(42)代入式(41)中,得

将式(43)代入式(39)、(40)中,得
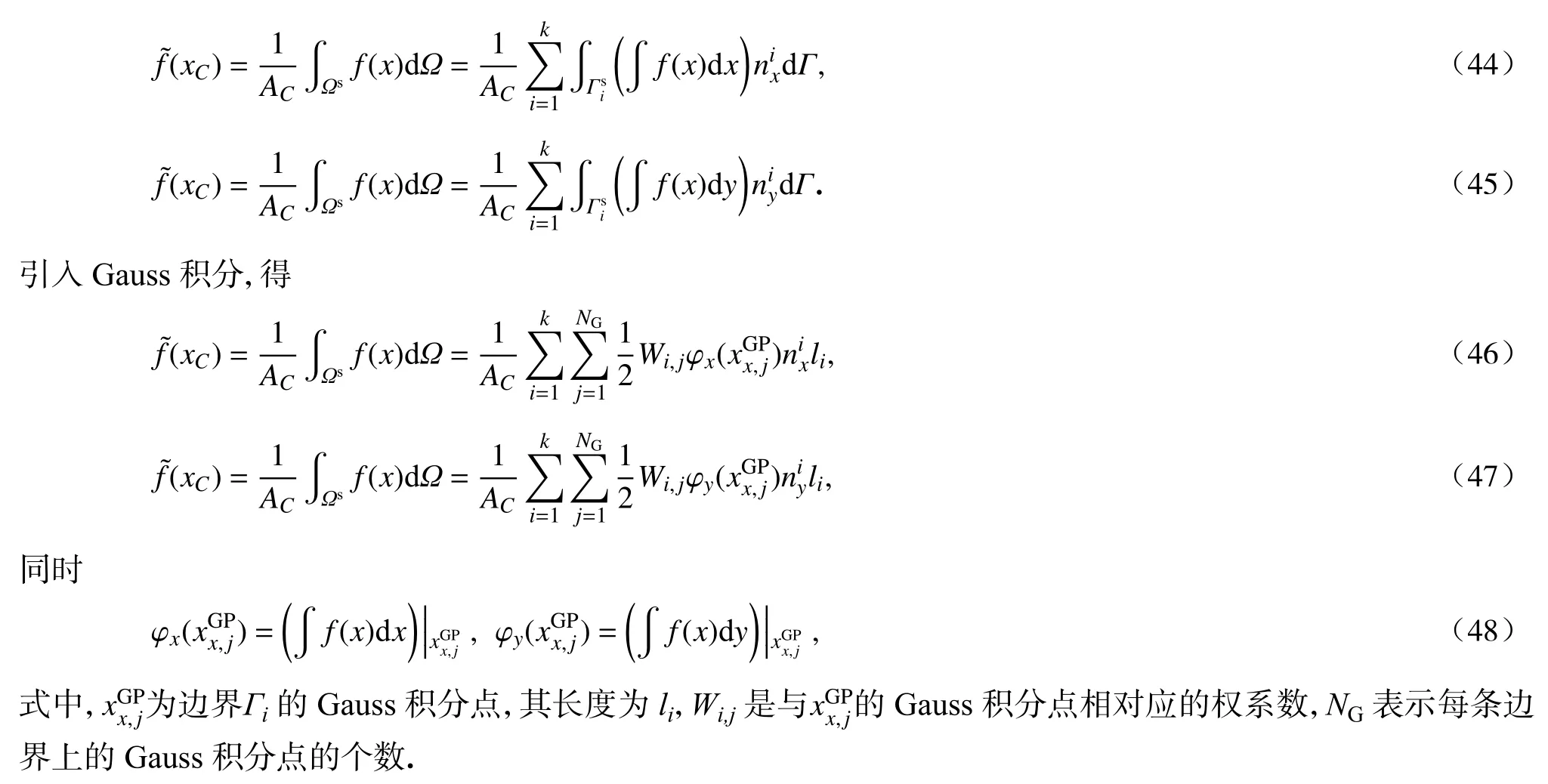
3 基于REG-DSG3 的有限元方程
假设求解域Ω离散为Ne个单元,求解域这些单元网格共有Neg条边,将每条边的两个端点
和这条边相邻的两个三角形单元的中心相连接,这样就在三角形单元的基础上形成了Ns个基于边的光滑域,求解域光滑域的数目和三角形单元边的数目相等,即Neg=Ns,如图2 所示.

图2 三角形单元和基于边界的光滑域Fig.2 Triangular elements and smoothing domains associated with edges
利用边界光滑技术和DSG 单元,层合板自由振动控制方程中的应变矩阵可表示为
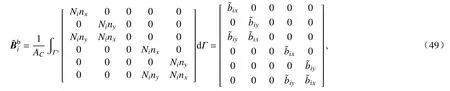
其中

式中,k表示每个光滑域的边界段数,对于求解域内边界处的边,k=3,对于求解域内部的边,k=4;Ni是与边界段m相关的三角形单元节点i的形函数.

其中

由此,光滑刚度矩阵为

同理,光滑质量矩阵可通过以下转换得到:

通过Gauss 积分,得

由此,层合板有限元控制方程中的矩阵都已沿光滑域的边界段进行光滑处理和计算,在计算过程中不需要坐标映射和Jacobi 矩阵的计算.
4 数值算例
下面通过数值算例分析复合材料层合板的自由振动问题.如无特殊说明,层合板各层具有相同的厚度,且由均匀线弹性复合材料构成,无量纲固有频率为.
4.1 算例1
首先以一长度为a、厚度为h的四边简支对称层合方板(0°/90°/90°/0°)为研究对象,探讨RES-DSG3 法在求解复合材料动力学问题时的收敛性和有效性.对于规则网格,α=0;不规则网格,α=0.4,其中α为定义在区间0 ~ 0.5 的不规则系数[20].相关的材料参数为E1/E2=10,20,30,G12=G13=0.6E2,G23=0.5E2,v12=0.25,ρ=1,剪切修正因子ζ=5/6.
由表1 可见,不同节点分布和不同弹性模量比时的四层层合板的一阶无量纲固有频率与文献[21]的一阶剪切理论的精确解很接近,具有较高的计算精度,表明了本文方法的有效性和收敛性.同时,网格“质量”对计算精度的影响很小,即使在极不规则的网格下也能获取稳定可靠的计算结果,进一步拓宽了该单元的使用范围.

表1 四层复合材料简支层合板的一阶无量纲固有频率Table 1 The non-dimensional 1st fundamental frequency of the simply supported 4-layer laminated composite plate
4.2 算例2
考虑三层对称层合方板(0°/90°/0°),边长为a,厚度为h,材料参数为E1/E2=40.采用17 × 17 网格离散求解域,对不同边界条件和不同边厚比条件下的板进行了数值计算.
表2 列出了通过本文方法计算的四边简支(SS),四边固支(CC),两对边简支、另两对边固支(SC)三种边界条件和不同边厚比的三层层合方板的一阶固有频率,并分别与文献[21-22]基于FSDT 的复合二次径向基函数法计算的结果进行了对比,具有较好的一致性.同时,表3 列出了三种边界条件下的前三阶固有频率,可以看出本文方法计算的无量纲固有频率与文献[23]基于高阶剪切变形理论计算的结果也很接近,验证了本文方法的有效性.

表2 三层复合材料层合板的一阶无量纲固有频率Table 2 The non-dimensional 1st fundamental frequency of the 3-layer laminated composite plate

表3 三层复合材料层合板前三阶无量纲固有频率(a/h=10)Table 3 The non-dimensional 1st 3 fundamental frequencies of the 3-layer laminated composite plate(a/h=10)
5 结论
本文将基于全局坐标的重构边界光滑DSG 单元用于复合材料层合板的自由振动问题分析.与原始的DSG 单元相比,该方法不需要对系统方程进行坐标映射,同时结合光滑技术将有限元矩阵的域积分简化为沿平滑单元边界的线积分.从数值计算结果来看,RES-DSG3 法在复合材料层合板自由振动分析时表现出良好的性能,具有较高的计算精度;即使是不规则网格,也能获得较好的结果,是一种有效可行的方法.此外,该方法中的光滑技术也可以扩展到其他问题的有限元框架内.

