PSO-BP神经网络的电力负荷预测研究

范国松， 齐正

(贵州中烟工业有限责任公司， 贵州， 贵阳 550000)

0 引言

电力负荷精准预测对于电力系统生产与发展具有重要意义，科学精准地预测电力负荷可提升电力系统运行经济性以及安全性。目前应用于电力负荷预测的算法众多，模糊负荷预测以及神经网络预测方法是目前广泛应用于电力负荷预测中的重要方法。BP神经网络是多层前馈网络，具有单向传播特性，其所具有的非线性映射能力以及自学能力可有效提升电力负荷预测精度，但BP神经网络容易陷入局部极小值，且训练速度过慢，影响电力负荷预测效率[1]。

近年来针对电力负荷预测的研究较多，李国庆等[2]研究基于随机分布式嵌入框架及BP神经网络的超短期电力负荷预测；郝晓弘等[3]研究混沌优化PSO-最小二乘支持向量机算法的短期负荷预测。2种方法均可实现电力负荷预测，且均具有预测过程中容易陷入局部极小值导致预测精度较低的缺陷。为提升电力负荷预测精度，研究PSO-BP神经网络的电力负荷预测，建立BP神经网络，利用粒子群优化算法优化BP神经网络，提升电力负荷预测精度。通过实例分析验证该方法具有较高的电力负荷预测精度，可应用于实际电力系统电力负荷预测中。

1 PSO-BP神经网络的电力负荷预测

1.1 BP神经网络

选取三层前馈网络作为电力负荷预测的BP神经网络，该神经网络中包含输入层、隐含层以及输出层。各层神经元与相邻层神经元存在连接，与层内神经元并未存在关联。利用无反馈连接方式作为各层神经元间的连接方式。BP神经网络输入与输出之间存在较高的非线性映射关系，用n与m分别表示输入节点数量以及输出节点数量，所建立的BP神经网络需实现n维空间至m维空间的映射。用X={x1,x2,…,xn}与Y={y1,y2,…,ym}分别表示n维输入矢量以及m维输出矢量；V={v1,v2,…,vn}与W={w1,w2,…,wm}分别表示输入层至隐含层间以及隐含层至输出层间权值矩阵；θi表示隐含层阈值；ρj表示输出层阈值；netj表示隐含层神经元接收其他神经元激励；netk表示输出层神经元接收其他神经元激励。隐含层所接受激励公式如下：

(1)

利用式(1)令隐含层获取新激活值bi，可得

(2)

式中，j=1,2,…,p，m与p分别表示输入层神经元数量以及隐含层神经元数量。

输出层神经元所接受激励公式如下：

(3)

式中，k=1,2,…,l，l表示输出层神经元数量。

式(3)令隐含层获取新激活值cj，可得：

(4)

g(x)表示转移函数，采用双极性Sigmoid函数作为转移函数，其公式如下：

(5)

通过以上过程建立三层前馈BP神经网络的数学模型。

1.2 粒子群优化算法

粒子群优化算法将优化问题之解设置为粒子，将各粒子所在位置设置为所需求解优化问题的潜在解[4]。设数量为m的粒子存在于d维的搜索空间内，d维空间内粒子i的位置用Xi=(xi1,xi2,…,xid)表示，且i=1,2,…,m；用Vi=(vi1,vi2,…,vid)表示粒子更改位置速率；粒子i在d维空间内最优位置用Pbest=(P1,P2,…,Pd)表示；用Gbest=(G1,G2,…,Gd)表示全部粒子中最优位置。粒子利用跟踪2个最优值实现每次迭代过程中位置更新。粒子速度更新公式如下：

Vij(t+1)=ωVij(t)+C1R1(Pj(t)-Xij(t))

+C2R2(Gj(t)-Xij(t))

(6)

粒子位置更新公式如下：

Xij(t+1)=Xij(t)+Vij(t+1)

(7)

式中，t与Xij(t)分别表示迭代次数以及迭代次数为t时粒子当前位置，Vij(t)与ω分别表示迭代次数为t时粒子运动速度以及惯性权重，C1与C2分别表示调节向全局最优粒子方向以及个体最优粒子方向飞行最大步长的学习因子，设C1=C2=2，R1与R表示在[0,1]区间变化的随机数。

依据以上公式实现粒子速度与位置更新，直至符合终止迭代条件[5]。可设置粒子群所搜索最优位置符合规定的最小误差标准要求以及最大迭代次数作为迭代终止条件。

粒子群算法中的惯性权重ω可实现当前速度受历史速度控制的影响程度，平衡粒子群算法的局部搜索能力以及全局搜索能力[6]。粒子群算法在惯性权重较大以及较小时分别具有较强的全局搜索能力以及局部搜索能力。惯性权重为0时，粒子群算法容易提前收敛。利用改进非线性动态自适应算法确定最佳惯性权重，令惯性权重可随适配值而自动调节，惯性权重计算公式如下：

(8)

式中，fave表示适应度函数。

1.3 PSO-BP神经网络预测模型

1.3.1 历史负荷数据预处理

建立PSO-BP神经网络预测模型前需预处理历史电力负荷数据、过滤错误数据以及异常数据[7]。电力负荷数据中存在错误数据以及异常数据时，将影响电力负荷预测结果精准性。选取Sigmoid函数作为BP神经网络激活函数，实现输入信号的非线性映射，该函数数值区间为[0,1]。为避免神经元存在饱和情况，提升电力负荷预测精度，需归一化处理网络模型待训练的输入负荷数据，令所输入电力负荷数据处于[0,1]间。时间为t时，Xi表示原始电力负荷数据，归一化处理原始电力负荷数据公式如下：

(9)

式中，Xmax与Xmin分别表示最大电力负荷以及最小电力负荷，Xi与t分别表示待归一化数据以及电力负荷时间。

利用相对误差公式评估负荷预测结果，相对误差公式如下：

(10)

式中，yi与yk分别表示预测电力负荷值以及实际负荷值，reeor表示相对误差。

1.3.2 电力负荷预测模型

采用粒子群优化算法优化的三层BP神经网络建立电力负荷预测模型，设置输入层神经元数量以及输出层节点数量均为24个，与每日24小时电力负荷相对应，隐含层节点设置为10。建立电力负荷预测模型过程如下：

(1) 设置BP神经网络基本参数，确定BP神经网络拓扑结构；

(2) 对粒子群优化算法实施初始化，初始化数量为N的粒子信息。将神经网络参数初始化，确定粒子群算法适应度值，确定粒子群内粒子最优个体位置以及全局最优位置；

(3) 依据从小到大顺序排序粒子群内粒子；

(4) 保留适应度值较高的数量为N/2的粒子；

(5) 用N表示所设定粒子总数量，当N与所保留粒子总数量相同时，执行步骤(6)；否则利用未保留粒子返回至步骤(2)；

(6) 依据式(6)、式(7)更新粒子位置以及粒子运动速度[8]，获取粒子相应适应度值；

(7) 判断误差是否低于ε以及是否达到最大迭代次数，当满足以上要求时，继续执行步骤(8)，否则转回至步骤(3)；

(8) 将所输出粒子信息设置为BP神经网络初始阈值以及初始权值；

(9) 训练三层BP神经网络，计算实际值与预测值间误差；

(10) 判断BP神经网络所输出结果是否符合最小误差要求，不符合要求时，转回至步骤(8)继续迭代，符合最小误差要求时，终止迭代，执行步骤(11)；

(11) 结束电力负荷预测模型训练，输出电力负荷预测结果。

2 实例分析

选取贵州某电力公司2018年10月—2019年10月电力负荷数据作为电力负荷预测的历史负荷数据，利用历史负荷数据实现该电力公司电力负荷预测。采用MATLAB仿真软件对数据进行训练和仿真，设置惯性因子为0.6，学习参数为0.07，粒子群初始粒子数量为80，最大进化迭代次数为500。利用训练好的神经网络模型进行预测。选取随机分布式方法(文献[2])以及混沌优化方法(文献[3])作为对比方法。

采用本文方法预测电力负荷的适应度函数值变化过程如图1所示。从图1实验结果可以看出，初始迭代时本文方法所获取的适应度函数值高达4.0以上，迭代次数下降迅速，直至迭代次数提升至20次之后，适应度函数值逐步下降，直至迭代次数为60次时，适应度函数值缓缓稳定，并降低至1.0以下。适应度函数值越低，电力负荷预测值与实际值越接近。实验结果有效验证本文方法具有较高的辨识精度，可提升电力负荷预测精度。

图1 适应度函数值变化

统计采用本文方法预测2019年11月16日该电力公司电力负荷与实际电力负荷对比曲线，结果如图2所示。

(a) 0—12 h

从图2实验结果可以看出，本文方法的电力负荷预测结果与实际电力负荷输出结果相差较小，实际输出结果与预测输出曲线极为接近，验证本文方法具有较高的电力负荷预测精度。

统计采用本文方法预测该电力公司2019年11月16日—21日电力负荷预测精度，并将本文方法与随机分布式方法以及混沌优化方法比较，结果如图3所示。从图3实验结果可以看出：采用本文方法预测电力负荷预测精度明显高于另2种方法，采用本文方法预测电力负荷预测精度均高于99%；采用另2种方法预测电力负荷的预测精度均低于98.5%。本文方法明显高于另2种方法的电力负荷预测精度，说明本文方法具有较高的电力负荷预测有效性。

图3 预测精度比较

统计采用本文方法预测该电力公司2019年11月16日—21日电力负荷的平均相对误差，并将本文方法与随机分布式方法以及混沌优化方法比较，结果如图4所示。

图4 平均相对误差比较

从图4实验结果可以看出，采用本文方法预测电力负荷的平均相对误差明显低于另2种方法，采用本文方法预测电力负荷的平均相对误差均低于0.5%，采用另2种方法预测电力负荷的平均相对误差均高于1%。实验结果再次验证本文方法具有较高的预测精度。

统计采用本文方法预测该电力公司2019年11月16日—21日电力负荷的迭代次数，并将本文方法与另2种方法比较，比较结果如图5所示。从图5实验结果可以看出：采用本文方法预测该电力企业2019年11月16日—21日电力负荷迭代次数均低于300次；采用随机分布式方法以及混沌优化方法预测该电力企业2019年11月16日—21日的电力负荷迭代次数均高于500次。实验结果有效验证采用本文方法预测电力负荷具有较少的迭代次数，说明本文算法具有较高的收敛效果。本文方法采用粒子群优化算法优化BP神经网络，具有可快速寻优的优势，收敛速度快。

图5 迭代次数比较

统计采用本文方法预测该电力企业2019年11月16日—21日的电力负荷的时间开销，并将本文方法与另2种方法比较，结果如图6所示。

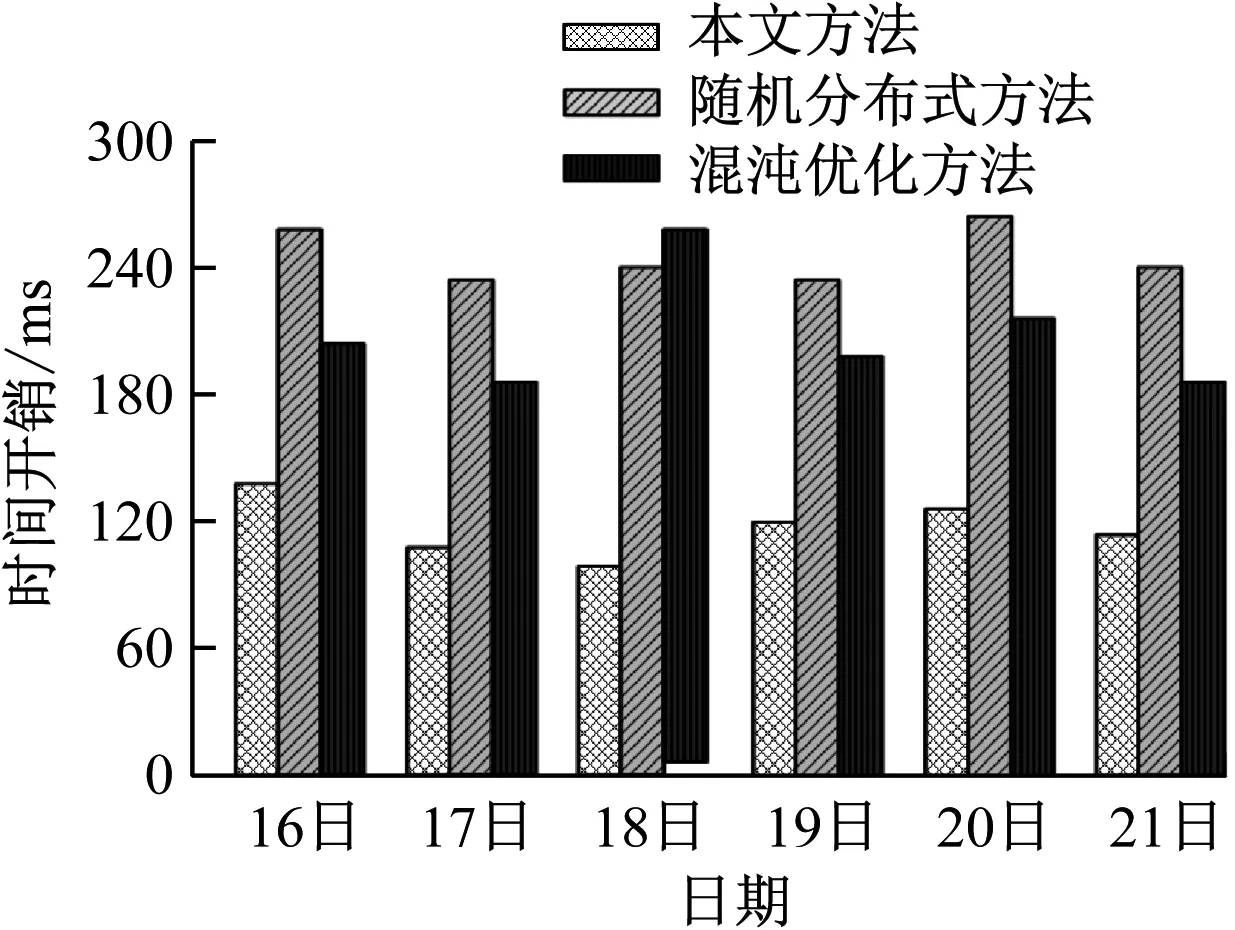
图6 时间开销比较

从图6时间开销比较结果可以看出，采用本文方法预测电力负荷所需时间开销均低于150 ms，电力负荷实时性可提升电力企业管理性能。图6实验结果有效验证本文方法预测电力负荷具有较高实时性。采用本文方法预测电力负荷，具有误差较低、收敛速度快、预测精度高的优势，可有效改善传统BP神经网络所具有的容易陷入局部极小点的缺陷。采用粒子群算法优化BP神经网络可有效提升BP神经网络的泛化能力，提升电力负荷预测准确率。

3 总结

电力系统运行的安全性和经济性可通过电力负荷精准预测提升，电力负荷精准预测可维持电力企业可持续发展，对国民经济发展同样具有重要意义。电力负荷预测具有极高复杂性，存在典型的非线性特性，其预测精准性、实时性以及鲁棒性极为重要。利用PSO-BP神经网络模型实现电力负荷预测，该模型利用粒子群优化算法提升BP神经网络预测性能，并将该模型应用于实际某地区电力负荷预测中。实例分析结果表明，该方法可有效提升电力负荷预测有效性以及精准性，可应用于电力企业电力负荷实际应用中，具有较强的现实指导意义以及工程应用价值。由于电力系统的负荷具有较强的复杂性，对预测的性能要求较高，本次研究未对设计模型的鲁棒性进行考虑，基于上述考虑，未来研究还将进一步改进，以提高设计模型对不确定性电力系统的适用性。