中国股市情绪与农期指数的风险传染和溢出测度

刘祥东，潘 飞，杨玉洁

［1.北京科技大学，经济管理学院，北京 100083；2.香港中文大学（深圳），深圳高等金融研究院，广东 深圳518063］

一、引言

农产品期货是世界上最早上市的期货品种，期货市场最早产生于农产品市场，而在此后的期货发展中，农产品期货成为期货市场的重要组成部分。据中国期货业协会统计，2019 年，中国农产品期货共成交11.60亿手，成交金额达52.69万亿元，分别占全国期货市场总成交量和总成交金额的29.57%和18.13%，分别占商品期货市场总成交量和总成交金额的30.08%和23.85%。此外，中国农产品期货在国际上也占据重要地位。据美国期货业协会(FIA)统计，2020 年中国农产品期货包揽了农产品期货交易量的前10名，有14种农产品跃居农产品期货交易量的前20 名，包括豆粕、棕榈油、玉米、豆油、菜籽粕、鸡蛋、白糖、棉花、菜籽油、橡胶、苹果、黄大豆1 号、纸浆期货和豆粕期权。

随着中国农产品期货市场的快速发展，它与国内外金融市场之间的联系也越来越密切。2004 年以来，金融资本大量投资于商品期货成为商品市场运作的新特点。随着机构投资者源源不断地介入大宗商品市场，其价格动态演化所呈现的特点已经远远超出了传统微观经济学均衡价格理论所能解释的范畴，有形商品交易越来越紧密地与金融运作交织在一起，而后者反过来在相当程度上决定了前者的价格演化，实现了大宗商品市场的金融化[1]。大宗商品价格长期由实需因素主导，短期由金融投机因素主导[2]，这种投机因素导致大宗商品期货的金融化[3]。针对大宗商品市场金融化现象，大量关于股票市场和大宗商品市场的实证研究结果表明，股票市场对大宗商品市场的确存在溢出效应[4-6]。尤其是在2008 年金融危机之后，股票市场对大宗商品市场的波动溢出效应显著增加[1,7-8]，而在这些研究中，也有学者选择农产品作为大宗商品市场的代表[7-8]。上述研究结果都证明了Adams 和Glck[9]的观点：大宗商品投资的大量流入，即金融化现象，改变了商品与普通股票市场之间的行为和依赖结构。

中国股票市场成立时间较晚，股市投资者结构与国外成熟市场有较大不同。与国外成熟市场相比，中国股市投资者结构中的个人投资者占比较高，市场更加容易被情绪感染，股市投资者情绪在股票市场定价中扮演着重要角色。在过去的20 多年里，大量基于投资者情绪的实证研究表明，股市的投资者情绪对资产价格的形成产生影响[10-15]。尤其是近来Huang 等[16]对投资者情绪指数构建方法的改进，也取得了一定的突破，他们利用美国股票市场数据构建了基于偏最小二乘法的投资者情绪指数（PLS情绪指数），并通过与以往经常采用的基于主成分分析方法的投资者情绪指数（PC 情绪指数）进行比较分析，证实PLS 情绪指数在美国股票市场中可以获得更好的预测效果。投资者情绪指数构建是一个关键的基础性研究，上述结果为基于投资者情绪的相关理论和实证研究提供了有力工具。

在此背景下，考虑到资本市场之间的联动性，一些学者尝试研究金融危机背景下中美投资者情绪的传染[17]，以及国际原油价格波动对中国投资者情绪的传染[18]。尽管如此，关于中国股市投资者情绪与农产品期货市场之间的风险传染和溢出效应，鲜有文献开展相关的实证及理论分析。此外，在方法论上，通常采用的是单一copula方法，以及单一状态变量下的实证分析，不能很好地反映数据之间的相关结构。已有文献改进这些静态copula模型主要采用两种方法：第一种是在copula 函数中加入马尔科夫状态转换机制，允许copula函数随着时间变化，在不同状态之间进行转换[19-22]；第二种是对copula 的相依参数构建时变方程，允许copula 函数中的参数随着时间变化[23-26]。在实践中，Wang 等[27]认为copula函数中的时变参数不一定意味着在正相关和负相关机制之间进行相依转换，而运用具有马尔科夫状态转换机制的copula模型能够更好地刻画经济变量之间的相关结构。因此，为了更好地刻画投资者情绪与农产品期货市场的风险传染和溢出效应，本文采用一个基于Markov 转换的混合Clayton copula 相关性和风险测度模型，分析中国股市投资者情绪对农期指数的正向和反向动态相关结构，同时也将该模型的实证结果与其他几类copula模型的结果进行比较，在分析完中国股市投资者情绪和农期指数的相关结构后，通过计算农产品期货指数收益的VaRs和CoVaRs来度量两者之间的风险溢出。

与已有文献相比，本文的贡献主要体现在以下两个方面。（1）采用基于Markov 转换的混合Clayton copula 相关性测度模型检验了中国股市投资者情绪与农期指数之间的风险传染效应，发现两者之间存在Markov 转换下的两种相关结构状态，在主要状态下呈现弱时变正相关关系。（2）采用基于Markov 转换的混合Clayton copula 风险溢出测度模型，检验了中国股市投资者情绪与农期指数之间的风险溢出效应，发现这些风险溢出效应具有显著的非对称性，即中国股市投资者情绪的上升或下降对于农产品期货的影响并不一致。这些结果对于两个市场的金融监管和金融投资均有一定的参考价值。

余文安排如下：第二部分介绍基于Markov 转换的混合Clayton copula 的风险传染和风险溢出测度模型的构建；第三部分利用该模型实证研究中国股市投资者情绪与农期指数的风险传染与溢出效应；第四部分分析中国股市投资者情绪与农期指数之间的风险传染机制；第五部分为本文的结论和政策建议。

二、相关结构和风险溢出测度模型的构建

（一）边缘分布模型构建

根据样本数据的自身特点，分别在正态分布、T分布和GED 分布下选取ARMA(p,q)-GARCH(m,n)模型对中国股市的投资者情绪和农产品期货收益率序列进行边缘分布建模，ARMA(p,q)-GARCH(m,n)模型的表达式为：

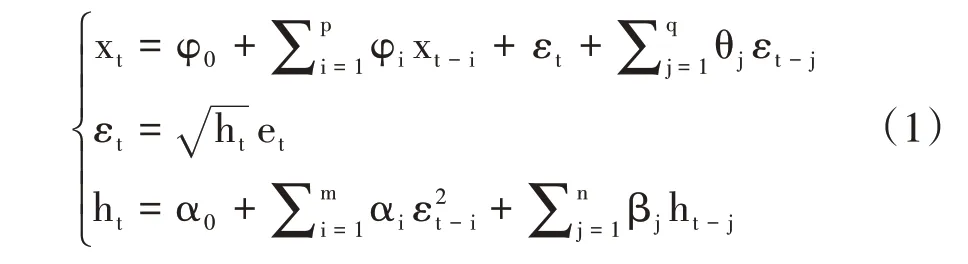
其中xt是相应金融时间序列的对数收益率序列，φi是自回归项系数，p 是自回归项的滞后阶数，θj是移动平均项系数，q 是移动平均项的滞后阶数，εt是残差，ht是残差的方差，而et是标准化残差，服从标准正态分布、T 分布或者GED 分布。αi是ARCH项系数，βj是GARCH 项系数，βj负责测量波动聚集性的大小，m和n分别是、ht的滞后阶数。

（二）Markov 转换的混合Clayton copula 函数的相关性测度

copula 函数是定义在[0,1]n、边缘分布服从[0,1]均匀分布的多元分布函数。为了捕捉非对称的尾部相关性，本文选择Clayton copula（CC0）、90 度旋转Clayton copula（CC90）、180 度旋转Clayton copula（CC180）和270 度旋转Clayton copula（CC270）来构建混合的Clayton copula。其中，Clayton copula 和180 度旋转Clayton copula 分别用于测量反映正相关关系的下—下尾相关性和上—上尾相关性，90 度旋转Clayton copula 和270 度旋转Clayton copula 分别用于测量反映负相关关系的下—上尾相关性和上—下尾相关性。根据Liu等[28]和Ji等[29]的工作，Clayton copula 和180 度旋转Clayton copula 构建的C1函数可以用来捕捉正相关性，90 度旋转Clayton copula 和270度旋转Clayton copula 构建的C2函数可以用来捕捉负相关性。这两个copula函数的表达式分别为：

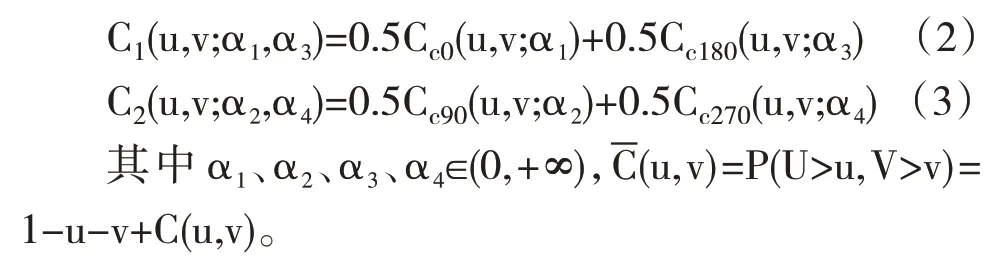
混合Clayton copula 为C1和C2函数之和，其表达式如下：

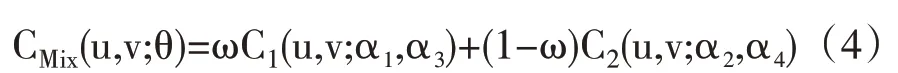
其中θ=(α1,α2,α3,α4)，ω 为权重参数。在混合Clayton copula 函数中，C1函数负责测量正相关性，α1和α3越大，正相关性越强；C2函数负责测量负相关性，α2和α4越大，负相关性越强。

考虑到金融市场相关性的动态特征以及可能的结构变化，本文在混合Clayton copula 函数的基础上引入一个状态转换机制，并假设其服从马尔科夫状态转换过程，从而构建Markov 转换的混合Clayton copula函数，其定义如下：

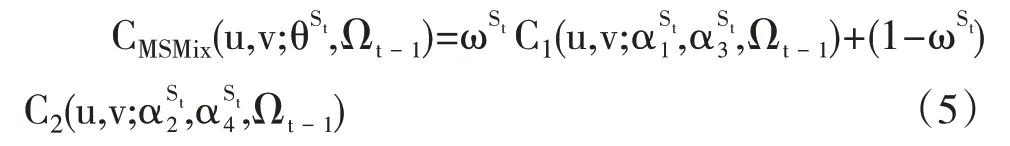
其中St是状态变量，Ωt-1是信息集，P(St；Ωt-1)是St在信息集Ωt-1中的预测概率，这里令P(St=1；Ωt-1)和P(St=2；Ωt-1)分别表示在t 时刻处于状态1 和状态2的概率，其表达式分别为：

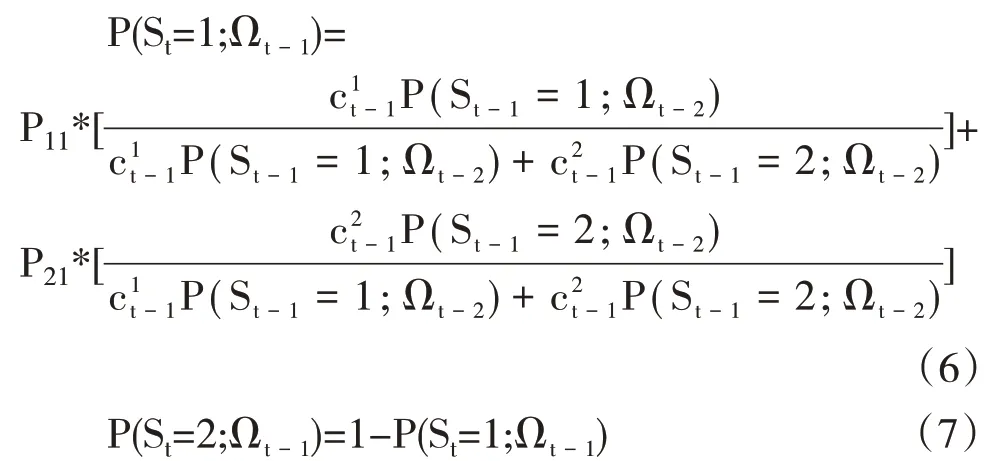
Markov 转换的混合Clayton copula 函数所含的参数较多，在极大似然估计法的基础上，采用内点法求最优解以完成参数估计。具体而言，可以采用两步法来进行参数估计：第一步是估计边缘分布模型中的参数，第二步是在给定边缘参数下估计copula参数[28,30]。

因此，参考Joe[31]的工作，可以给出基于Markov转换的混合Clayton copula 函数的四个尾部相关系数：

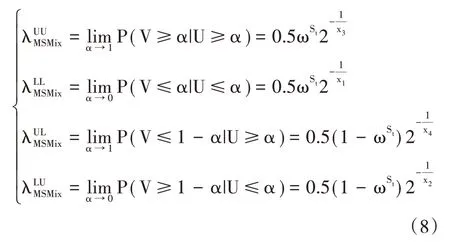
在下文的实证中，将采用这四个尾部相关性度量指标来测度中国股市投资者情绪向农期指数的风险传染。

（三）风险溢出的测度

这里将采用上（下）行VaR 和CoVaR 来度量股市投资者情绪对中国农期指数的风险溢出效应。设r1,t为时间t下农产品期货的对数收益率，参考Ji等[32]的工作，在给定尾部概率α 下，可以采用Pr(r1,t≤ 分别计算农产品期货收益的下行VaR 和上行VaR。本文通过ARMA-GARCH模型对金融时间序列进行边缘分布建模。

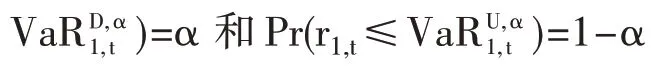
第一，若标准化残差服从标准正态分布，则可以得到r1,t的条件分布如下：

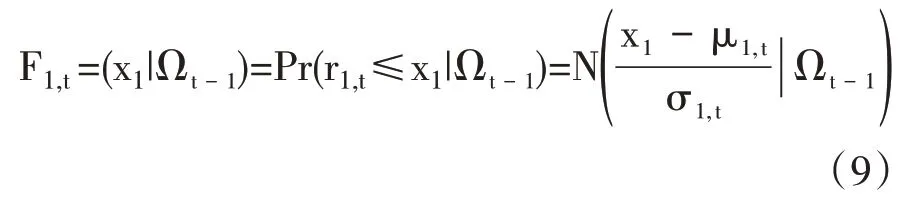
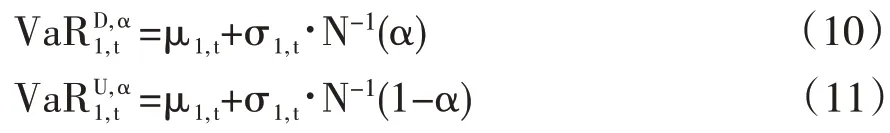
第二，若农产品期货收益在标准化残差服从标准T 分布或者GED 分布，则下行风险和上行风险的表达式分别为：

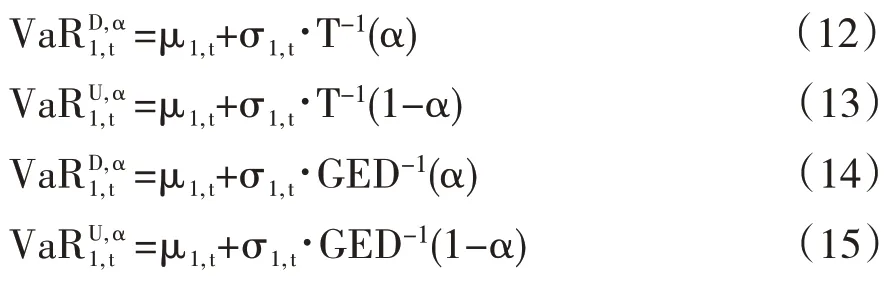
CoVaRs 为以股市投资者情绪指数的极端变化为条件的农产品期货收益的VaRs。设r2,t为时间t下的股市投资者情绪指数，参考Liu 等[28]、Ji 等[32]的工作，估计CoVaRs的方程如下：

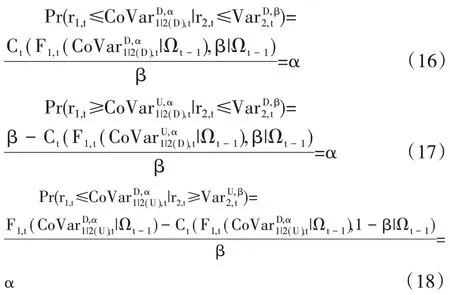
三、实证研究

（一）中国股市投资者情绪综合指数的构建

参考Yang和Zhou[33]的工作，本文选取上证综指和深证综指流通市值加权的相对强弱指数（RSI）、心理线指数（PSY）、交易量（VOL）和换手率（TR）作为中国股市投资者情绪的代理变量。为剔除宏观经济因素对投资者情绪指数的影响，分别利用中国股市的四个投资者情绪代理变量与居民消费价格指数（CPI)、工业品出厂价格指数（PPI）、工业增加值（IAV）和宏观经济景气指数（MBCI）进行回归分析，取其残差作为剔除宏观经济因素的投资者情绪代理变量。实证样本选自1996年10月至2019年6月的月度数据，所有数据均来自Wind 数据库。需要说明的是，这里选取投资者情绪的数据比最早的农产品期货的数据提前了28 个月，显著降低了构建的投资者情绪指数受初始数据的影响，以确保最终的两者相关性分析中采用的投资者情绪指数更为稳定。采用Huang 等[16]提出的基于偏最小二乘法的投资者情绪构建方法，通过两步回归得到投资者情绪综合指数SPLS：

表1 投资者情绪指数与上证综指、深证综指的Pearson相关性检验

表1 投资者情绪指数与上证综指、深证综指的Pearson相关性检验

注：***表示在1%的显著水平下拒绝无自相关的原假设

表1 的结果显示，SPtLS与沪深两市收益率均呈显著正相关关系，表明构建的投资者情绪指数能够有效表征中国股票市场的情绪变化。

（二）中国股市投资者情绪与农期指数的相关结构分析

本部分将实证研究股市投资者情绪与农期指数的相关结构。这里选择上市时间较长的8 种农产品期货价格指数：连豆指数（AFI）、豆粕指数（MFI）、郑棉指数（CFFI）、玉米指数（CFI）、豆油指数（YFI）、郑糖指数（SRFI）、菜油指数（OIFI）、棕榈指数（PFI），从而一共构成8 组实证研究，每组实证的时间长度为一种农产品期货价格指数和投资者情绪指数的时间交集。实证中对8 种农产品期货价格指数Pt进行对数化处理，从而得到其相对应的对数收益率序列，这些序列与投资者情绪指数的描述性统计结果如表2所示。

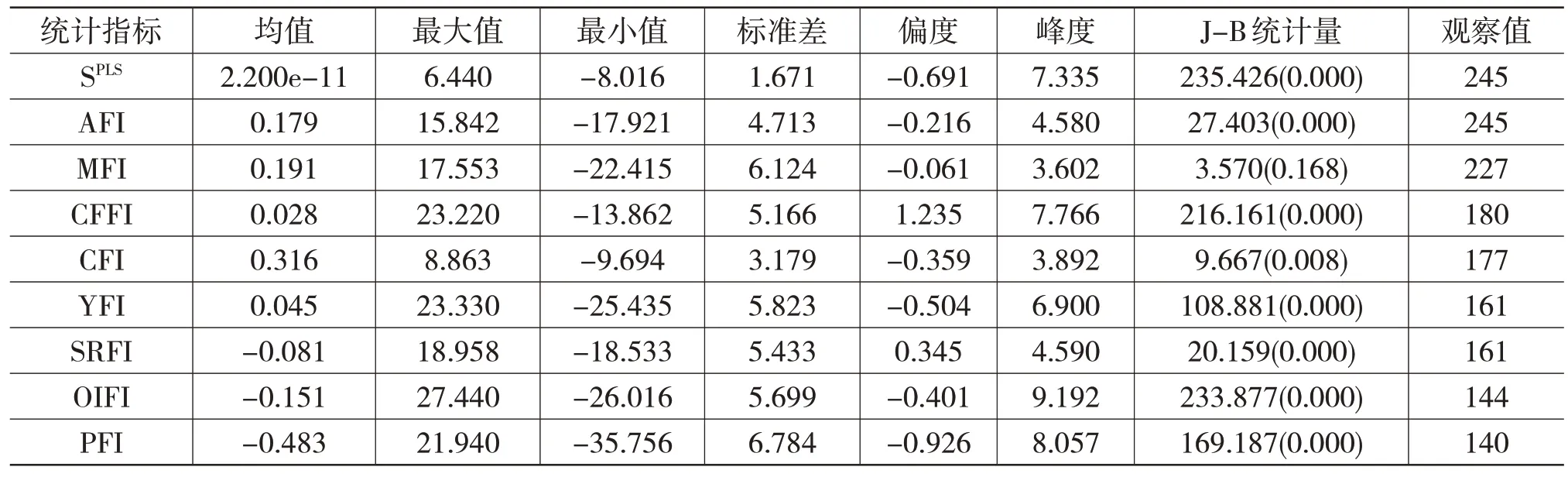
表2 投资者情绪指数与农产品期货价格指数对数收益率序列的描述性统计

表2 的结果显示，在8 种农产品期货中，连豆指数、豆粕指数、郑棉指数、玉米指数和豆油指数在样本区间内的平均对数收益率为正，其余3 种农产品期货指数的平均对数收益率为负。棕榈指数的标准差最大，可见该品种的市场波动性更强。9 个样本数据中，只有豆粕指数服从正态分布，其余均拒绝正态分布的假设，具有尖峰厚尾特征，且大多数表现为左偏。

接下来，对投资者情绪指数与农产品期货价格指数对数收益率序列进行三类检验：采用ADF 检验、PP 检验和KPSS 检验来综合考察变量的平稳性，采用收益率序列和收益率平方序列Ljung-Box 统计量来检验变量的自相关性，采用ARCH-LM 统计量来检验变量的条件异方差性。实证结果显示，每个变量都是平稳的，均存在自相关性或条件异方差性。限于篇幅，未在文中汇报实证结果。因此，利用ARMA(p,q)-GARCH(m,n)模型来建立边缘分布模型是合理的。

在运用Markov 转换的混合Clayton copula 模型来估计股市投资者情绪指数与农期指数之间的相关结构之前，首先利用6 种不同类型的单机制单一copula模型（包括正态copula、T copula、Clayton copula、90 度旋转Clayton copula、180 度旋转Clayton copula、270度旋转Clayton copula）和Markov转换的混合Clayton copula 模型，以及时变正态copula 和时变T copula 来估计股市投资者情绪指数与农期指数之间的相关结构。限于篇幅，这里仅汇报了时变正态copula、时变T copula 和混合Clayton copula 模型的估计结果。如表3所示，大部分参数估计值在1%的显著水平下是显著的，将时变正态copula、时变T copula的对数似然函数值，AIC值和BIC值与正态copula 和T copula 进行对比，可以发现除棕榈指数外，其他7个农产品期货的参数估计均在Markov转换的混合Clayton copula 模型下达到了最佳效果。综合来看，Markov 转换的混合Clayton copula 模型实现了更好的参数估计结果，这与Wang 等[34]、Charfeddine 和Benlagha[35]的研究结果一致，因为copula 函数中的时变参数不一定意味着在正相关和负相关机制之间进行依赖转换。

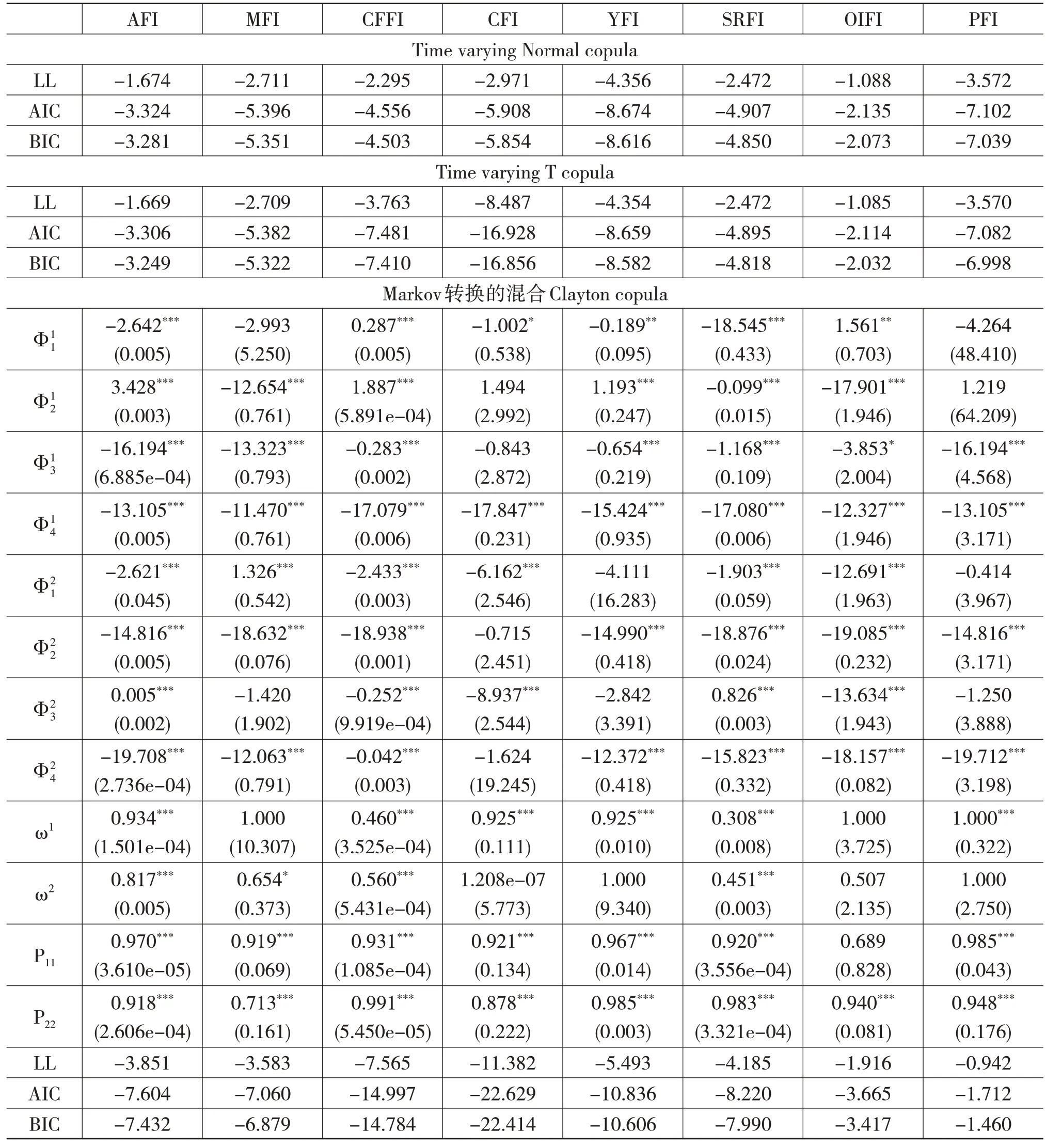
表3 几类copula模型的参数估计结果

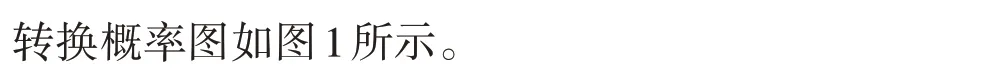
完成Markov 转换的混合Clayton copula 模型的参数估计结果之后，计算Markov 转换的混合Clayton copula 模型的四个尾部相关系数，具体结果汇报在表5中。

表4 Kendall秩相关系数和Pearson相关系数估计结果

表3 至表5 的结果显示，四种不同类型的Clayton copula 函数在相关结构分析中都发挥了作用；其中，表3 的参数估计结果显示，大多数参数估计值在1%的显著水平下显著。此外，图1 的状态转换概率图也显示，中国股市投资者情绪与农期指数之间不只是存在一种不变的状态。这些结果共同证明基于Markov 转换的混合Clayton copula 模型的有效性。值得强调的是，Markov 转换的混合Clayton copula 模型能够灵活地测量四种非对称的尾部相关性，因为在其构建过程中同时运用了Clayton copula、90 度旋转Clayton copula、180 度旋转Clayton copula 和270 度旋转Clayton copula；而时变正态copula、时变T copula 虽然能测量动态的相关结构，但不能测量非对称的尾部相关关系。

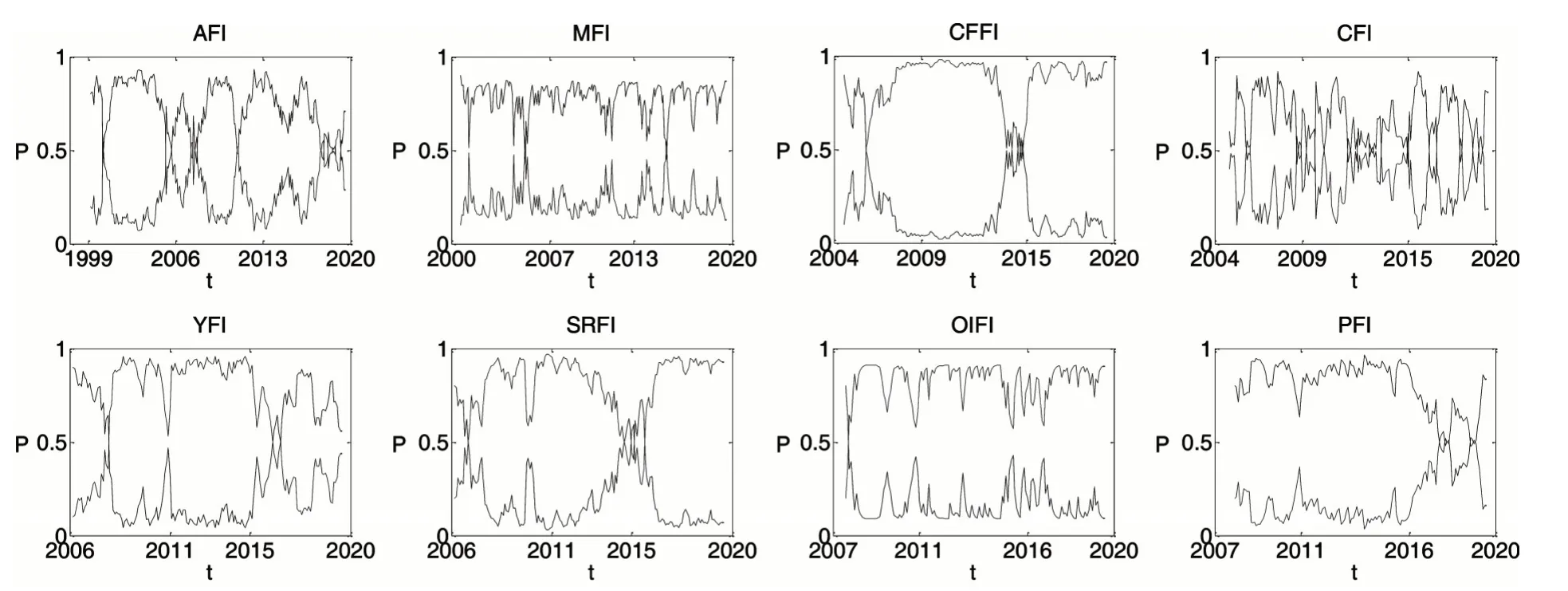
图1 投资者情绪指数与8种农产品期货价格指数的状态转换概率图

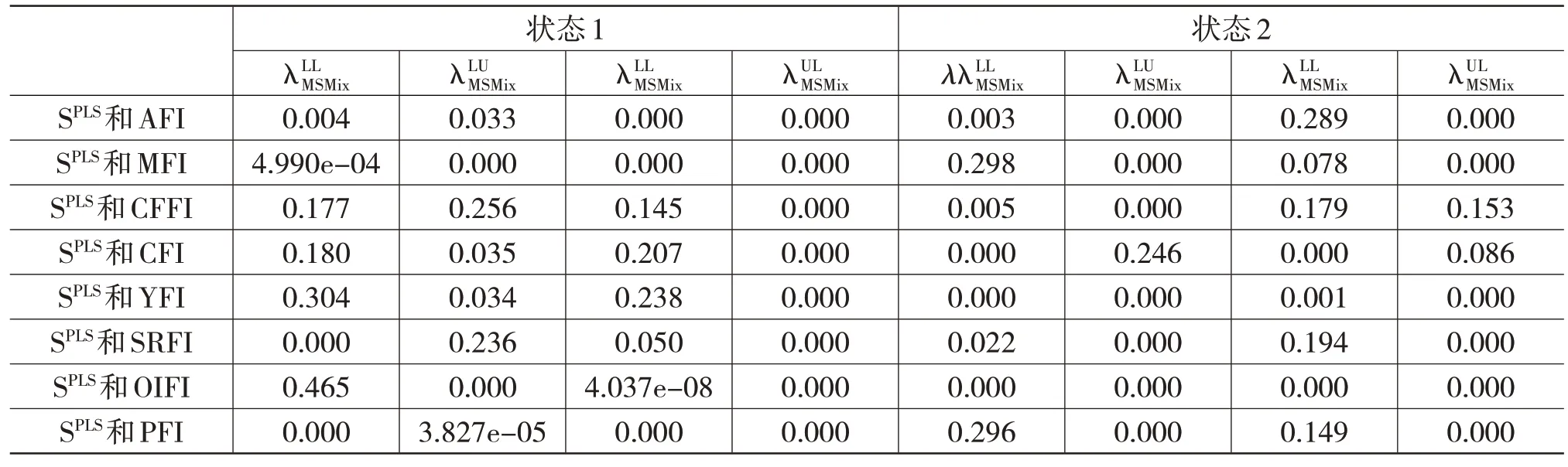
表5 投资者情绪指数与8种农产品期货价格指数的尾部相关系数

接下来，以中国股市投资者情绪指数与连豆指数的相关性为例，对实证结果进行详细分析。如表3 所示，每个状态下它们的相关结构都不相同，比如在状态1 下的参数估计值是-2.642，在状态2 下的参数估计值是-2.621；在状态1 下的参数估计值是3.428，在状态2下的参数估计值是-14.816。P11和P22分别表示P(St=1|St-1=1)和P(St=2|St-1=2)的值，可用来描述两种状态持久性的高低，结果显示，状态1和状态2的持久性相当。

如图1 所展示，中国股市投资者情绪指数和连豆指数相关结构的两种状态转换概率一直此消彼长；在大多数时间区间内，状态1 的概率基本大于状态2 的概率；但在2001 年加入世贸组织、2003 年“非典型肺炎”暴发、2008 年金融危机、2018 年中美贸易摩擦的几个关键时点，情况发生反转，状态2 的概率在短期内大于状态1 的概率，出现结构突变点。在状态1下，权重参数ωSt的值为0.934，Markov转换的混合Clayton copula函数的Kendall秩相关系数为-0.001，Pearson 相关系数为-0.0.002。在极端市场条件下，描述同向协同运动强度的上—上尾相关系数和下—下尾相关系数分别为0 和0.004，而描述反向协同运动强度的下—上尾相关系数和上—下尾相关系数分别为0.033 和0。而在状态2 下，权重参数ωSt的值为0.308，Markov 转换的混合Clayton copula 函数的Kendall 秩相关系数为0.211，Pearson 相关系数为0.232。在极端市场条件下，描述同向协同运动强度的下—下尾相关系数和上—上尾相关系数分别为0.003 和0.289，而描述反向协同运动强度的下—上尾相关系数和上—下尾相关系数均为0。这些结果表明，状态2 的正相关性比状态1 强，说明几次重大历史事件的节点后，股市投资者情绪指数对连豆指数的影响增强。图2 中中国股市投资者情绪指数与连豆指数的相关系数图的结果也显示，两者平滑相关系数基本上都处于0.02 的上方，意味着中国股市投资者情绪指数和连豆指数呈正相关关系，且相关系数在几个突变点处突然增强，表明突发事件提升了投资者情绪指数与连豆指数之间的相关性。

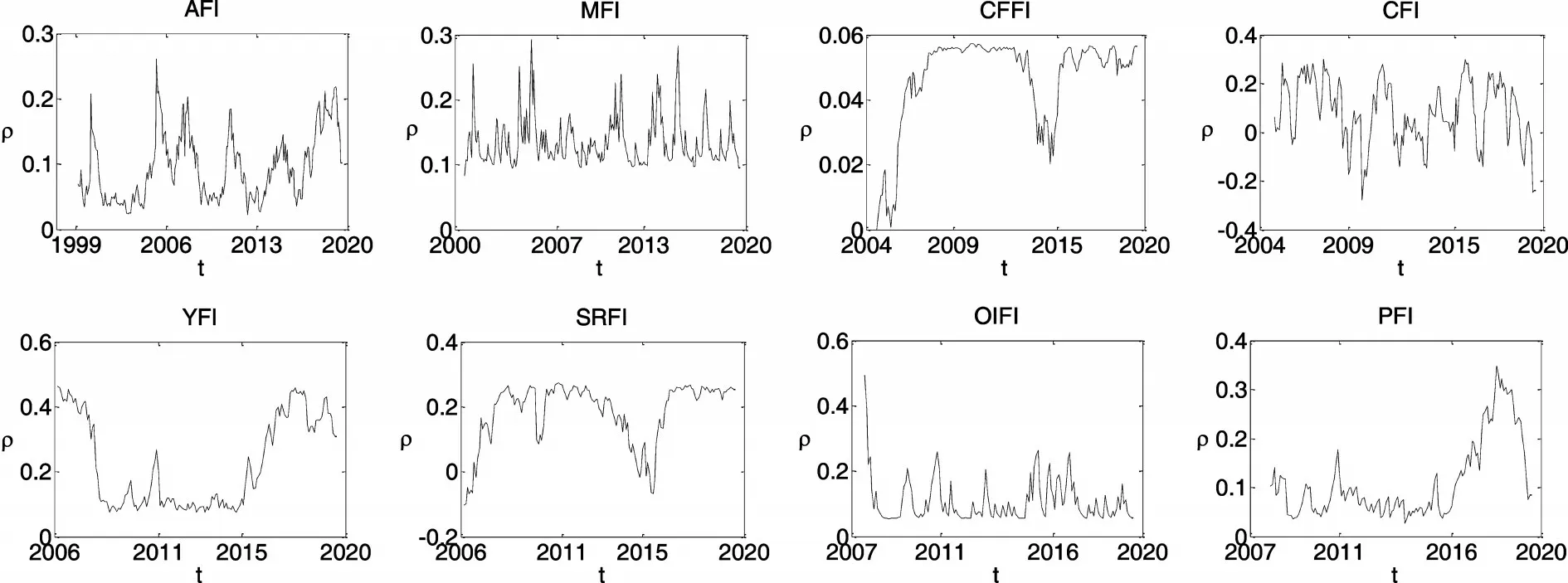
图2 投资者情绪指数与8种农产品期货价格指数的相关系数图

按照相同的步骤和分析方法，其余7 种农产品期货价格指数与中国股市投资者情绪指数均呈正相关关系，只是这种相关性并不强。总体来看，股市投资者情绪指数和农期指数之间呈正相关关系，且这种正相关关系随时间的改变不断变化，呈现出时变正相关性，但整体上来看这种正相关关系并不强。

（三）中国股市投资者情绪对农期指数的风险溢出

本部分通过计算农产品期货收益的VaRs 和CoVaRs 来度量两者之间的风险溢出。这里选取α=β=0.05。图3 描述了不同中国农产品期货收益在股市投资者情绪指数极端变化条件下的VaRs 和Co-VaRs 的轨迹。在这8 组数据中，都小于，而都大于，意味着在股市投资者情绪指数极端变化条件下，中国农产品期货收益的风险更大，体现的是正向的风险溢出效应，与正相关结构相对应。从图3 中可以看出，郑糖指数、菜油指数和棕榈指数的VaRs和CoVaRs的数值呈收敛的趋势，表明风险随时间在逐渐减小，而连豆指数、豆粕指数、郑棉指数、玉米指数、豆油指数的VaRs和CoVaRs的数值则呈震荡的趋势，在某些时刻风险会被放大，比如连豆指数、豆粕指数和豆油指数在2008 年金融危机期间风险便被放大，可见豆类农产品受金融危机影响较大。一般情况下上行VaR和上行CoVaRs 的数值为正。最后，观察图3 中上行Co-VaRs 和下行CoVaRs 的轨迹，整体上可以发现中国股市投资者情绪带给农期指数的风险溢出效应具有非对称性，比如连豆指数和郑棉指数上行风险溢出效应更大，豆粕指数下行风险溢出效应更大，但也有个别从图形中不太好判断的，比如豆油指数。

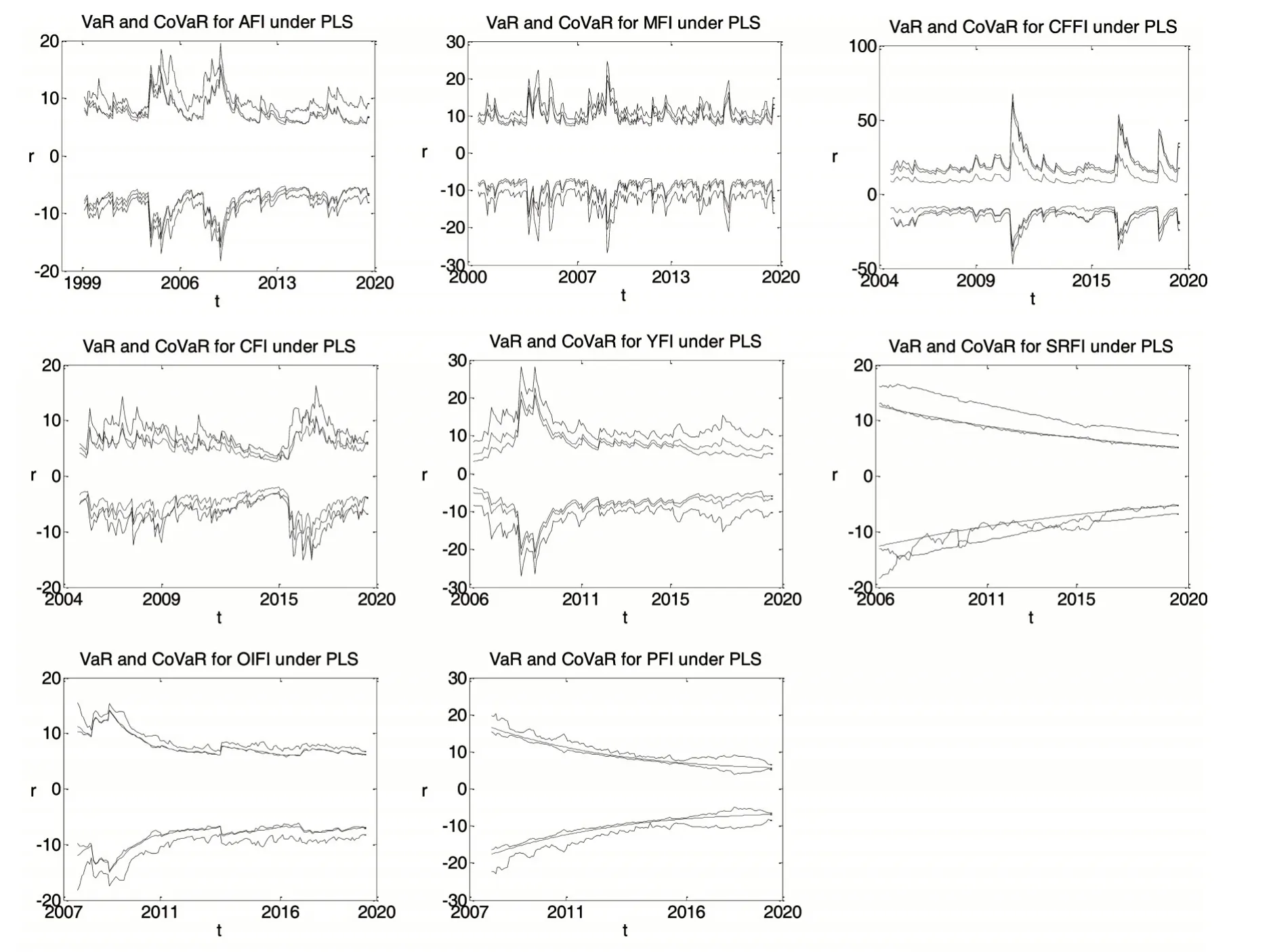
图3 中国农产品期货收益的VaRs和CoVaRs

表6 CoVaR/VaR 和CoVaR/VaR 的汇总统计

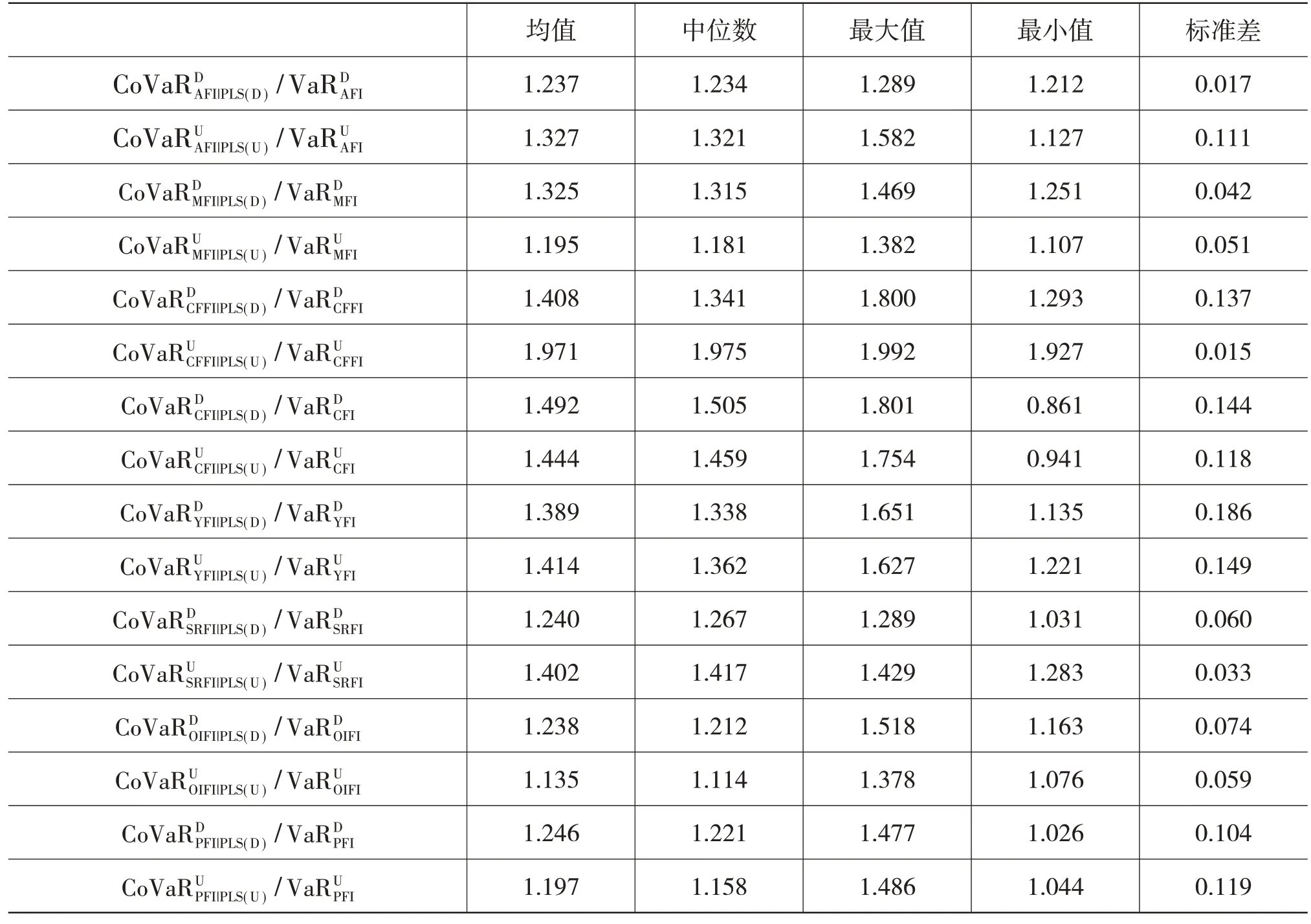
表6 CoVaR/VaR 和CoVaR/VaR 的汇总统计

为了检验风险溢出效应的显著性和非对称性，采用Kolmogorov-Smirnov(K-S)检验，检验结果如表7所示。

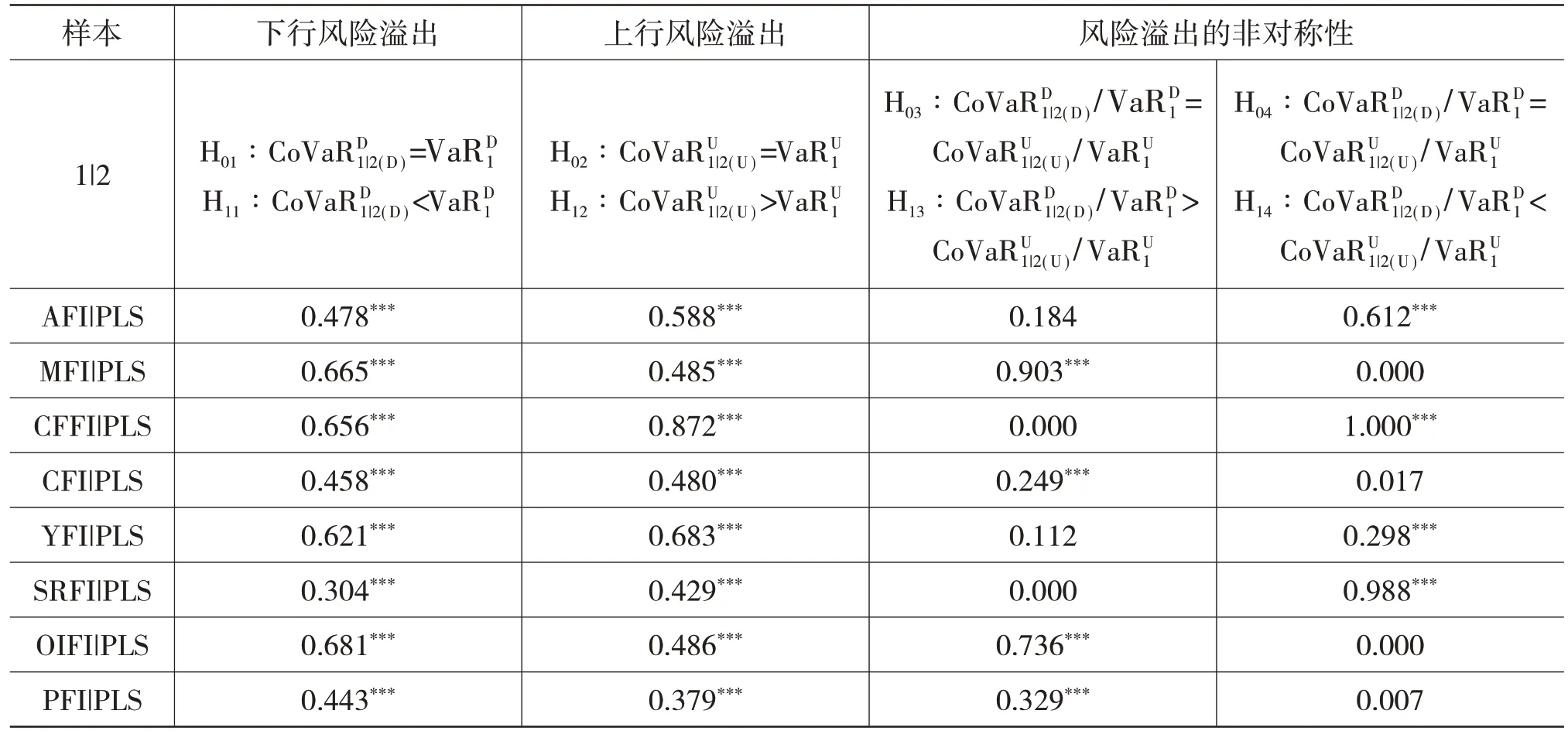
表7 中国股市投资者情绪对中国农产品期货收益的风险溢出和非对称性检验

在表7 中，第二列和第三列用来检验股市投资者情绪是否对农期指数收益存在正向的风险溢出效应，第四列和第五列则用来检验风险溢出效应的非对称性。表7 的第二列和第三列的结果表明，中国股市投资者情绪对8 种农产品期货指数收益均存在显著的正向风险溢出效应。而根据第四列和第五列的结果，可以看出中国股市投资者情绪对这8 种农产品期货指数收益的风险溢出效应具有非对称性，其中中国股市投资者情绪对豆粕指数、玉米指数、菜油指数、棕榈指数的下行风险溢出效应更大，对连豆指数、郑棉指数、豆油指数、郑糖指数的上行风险溢出效应更大。这些结果说明在实践中，中国股市投资者情绪对不同农产品期货指数收益的影响不尽相同。总体来看，中国股市投资者情绪对农期指数收益具有显著的正向风险溢出效应，且这种风险溢出效应具有非对称性。

四、中国股市情绪与农期指数风险传染机制分析

从金融市场一体化角度来看，随着经济一体化的发展，资本的流动加速、信息技术的日新月异，资本市场之间的关联更加紧密，股票市场投资者情绪反映了投资者对市场的预期情况，大量实证研究表明投资者情绪变化能够在一定程度上影响股票价格的变动，因此，股市投资者情绪的变化可能会迅速传导并影响整个金融市场。从本质上来看，股市投资者情绪向农期指数的传染具有深层次的经济逻辑和具体的传播途径。

一是股市和农产品期货市场定价具有共同的定价因子，也有不同的定价因子，当共同定价因子波动时，两个市场很可能发生联动，而股市投资者情绪能够在市场联动中推波助澜。从大类资产定价的角度而言，根据永续迭代的股利贴现模型，股票市场定价主要受分子端的净资产、净资产收益率、股利分红率，以及分母端的利率水平、风险偏好（受投资者情绪影响）、盈利增速、产业周期等因素的影响。而农产品期货的定价主要受基本面中的供给、需求、库存、通胀水平、利率水平、投资者情绪等因素的影响。其中，宏观经济基本面的强弱影响上市公司盈利水平，也影响农产品市场的需求，是影响股市定价和农产品期货市场定价的共同因子。宏观经济基本面情况越好，股市的表现越好，农产品期货市场的表现也越好。但也有一些因子，如通胀水平对股市和农产品期货市场可能产生相反的影响。尽管如此，在这些宏观变量影响股市的过程中，股市的投资者情绪将起到股市震荡放大器的作用，加大股市的上扬或下跌表现，并通过股市和农产品期货市场的联动效应，传染至农产品期货市场，影响农产品期货价格指数走势。

二是农业相关的上市公司股价和农产品期货之间具有产业链条的联动效应，股市投资者情绪可以通过这种产业链的联动效应将股市的风险传染至农产品期货市场。研究发现，随着农业现代化的发展，农业产业链日臻完善，主要包含农产品的原料、加工、生产、运输、销售等各个环节。从产业链联动的角度看，农业部门及其上下游的产业资产价格的变动，都可能会影响到农产品期货价格的走势，并且农业相关上市公司股价的变化，对农产品期货市场的影响更为直接，其传导机制不是依赖股市和农产品期货市场的市场联动，而是通过农业产业链相关链条间的相互影响和传导。当然，与农业产品核心板块相关的上市公司股价的变化对农产品期货价格的影响会更大一些，其中，股市投资者情绪将通过放大农业相关产业链上市公司股价的变化，进一步将风险传染到农产品期货市场。

三是股市投资者情绪在投资者人群之中通过多种媒介传播，进而传染到农产品期货市场。一方面，股市和农产品期货市场中具有一部分共同的机构和个人投资者，股市投资者情绪可以通过共同投资者快速传染至农产品期货市场，影响农产品期货价格走势。在资本市场中，一部分机构投资者和个人投资者同时拥有股票和农产品期货交易账户，他们可能会在两个市场中同时进行交易操作，或者是同时关注这两个市场，如此一来，股市投资者情绪不仅影响其在股票市场的交易，也会影响其在农产品期货市场的交易决策，从而影响农产品期货价格指数的走势。另一方面，股市投资者情绪也可能通过股吧、短视频、微信公众号、微博等多种媒介进行信息传播，进而影响到农产品期货市场交易者的投资决策，最终影响到农产品期货价格的走势。

值得注意的是，股市投资者情绪在农产品期货市场中的传染，势必会导致农产品期货市场的风险溢出效应，而投资者对于悲观和乐观情绪的反应程度不同，也导致了风险溢出效应呈现出非对称性。

五、结论及政策建议

本文应用一个基于Markov 转换的混合Clayton copula 相关性和风险测度模型度量中国股市投资者情绪与农期指数的风险传染与溢出效应。其中，混合 的Clayton copula 由Clayton copula、90 度旋转Clayton copula、180 度旋转Clayton copula 和270 度旋转Clayton copula 构成，它们能够同时测量四个尾部相关性，从而有效连接对称和非对称的尾部相关关系。与此同时，加入具有状态转移概率的马尔科夫链过程，使得相关性和风险测度模型可以捕捉变量之间的正相关和负相关关系，并且基于相关结构分析运用VaRs 和CoVaRs 指标进行风险度量，通过与其他几类copula模型的实证比较，得到以下结论。

第一，四种不同类型的Clayton copula 函数在相关结构分析中都发挥了作用，大多数参数估计值在1%的显著水平下是显著的，状态转换概率图也显示股市投资者情绪指数与中国农产品期货市场之间不仅仅只是存在一种不变的状态。这些结果都证明了Markov 转换的混合Clayton copula 模型的有效性。在不同模型的对比分析中，基于Markov 转换的混合Clayton copula 相关性测度模型比单一copula 模型、混合copula 模型和其他两种动态copula 模型的表现更好。

第二，连豆、豆粕、郑棉、玉米等8 种农产品期货价格指数与我国股市投资者情绪指数之间在Markov状态转换下呈现两种相关结构，在主要状态下两者之间呈正相关关系，且这种正相关关系随时间的改变不断变化，可称之为时变正相关性，但整体上来看这种正相关关系并不强。

第三，在风险度量方面，股市投资者情绪对8 种农产品期货价格指数有显著的正向风险溢出效应。同时，这种风险溢出效应具有非对称性，其中股市投资者情绪对豆粕指数、玉米指数、菜油指数、棕榈指数的下行风险溢出效应更大，对连豆指数、郑棉指数、豆油指数、郑糖指数的上行风险溢出效应更大。

股市投资者情绪已经成为影响股市资产定价的重要因素之一，由于共同投资者、股市与农产品期货市场之间共同定价因素、资本市场之间的联动性等原因，股市投资者情绪会传染至农产品期货市场，并形成风险溢出效应。为了促进我国股市和农产品期货市场的稳健发展，建议未来重视下述方面的工作。

第一，构建科学的股市投资者情绪指标体系，加强对中国股市投资者情绪的监测和管理。在基于股利贴现模型的股票资产定价框架中，投资者情绪位于定价公式的分母端，股市的投资者情绪越高，股价越容易被高估，反之则相反。投资者情绪的非理性波动将会导致股票市场的异常波动。因此，建议监管部门要结合股市的实际情况，构建科学的投资者情绪指标体系；根据投资者情绪指数的高低，划分不同层级的风险等级标志；当投资者情绪运行至警示区间时，对市场中的机构和个人投资者发出警示信息，提示市场风险；当投资者情绪运行至危险区间，可能诱导发生金融系统性风险时，及时报告上级部门出台相关措施，化解潜在危机。

第二，加强对股市和农产品期货市场的联动监察，做好风险传染的监测和管理。股市的投资者情绪可能通过共同投资者、农业相关行业联动等因素传染至农产品期货市场。因此，为了促进农产品期货市场的稳定发展，建议在建立健全股市投资者情绪监测、预警和应急系统的基础上，在监管内部要将相关的股市投资者情绪信息共享给农产品期货市场监管部门，做好金融市场监管体系内的信息共建和共享；当股市投资者情绪监测发出预警信号时，要及时阻止农产品期货市场中的虚假信息通过各种网络渠道传播，及时传递市场的正确信息以正视听，严厉打击各种利用虚假信息操纵市场的交易行为；要积极引导机构投资者加入农产品期货市场，发挥机构投资者稳定市场的作用。

第三，加强投资者教育，培养理性投资理念。在中国股市个人投资者的比重较高，截至2021 年年末，A 股中个人投资者占比达47.2%，这一数量远超发达经济体资本市场。股市中个体投资者缺乏对金融市场的正确认知、相关投资知识体系的不完备是导致非理性情绪产生的根源。建议要加强投资者金融基础知识教育，帮助投资者形成正确的投资理念；完善市场参与准入，对于参与股市、农产品期货市场的个人投资者，设定准入的基础金融知识门槛；鼓励投资者持续参与金融基础知识学习和教育，对于满足特定资质认证的个人投资者在交易印花税等方面给予一定的优惠。