基于混沌理论的同步序列研究*

杨万峰 李含辉 易观理

（武汉船舶通信研究所 武汉 430205）

1 引言

同步在整个通信系统占有核心地位，同步接收的好坏关系到接收端性能的优劣，同步捕获的常用方法为自相关辅助序列同步法，其中辅助序列也称为同步序列，在同步捕获中有着极其重要的作用，标准MIL-STD-188-110C附录C数据帧的同步头部分包含184个同步8PSK符号用于实现同步和估计多普勒频移［1］，根据理论研究和仿真验证可知，这184个8PSK所组成的符号属于伪随机序列，是由m序列经过截断所生成的短截序列，具备很强的相关性，适合检测相关峰的方式实现同步［2］，但是m序列保密性和抗截获性能不高，非合作方可以通过测量接收序列的功率谱线间隔得到周期，继而得到m序列特征多项式［3］，Gold序列由于是m序列合成得到的，所以也存在类似的问题，MIL-STD-188-110C附录C中某些波形还采用了长度为32的Walsh正交序列作为同步前导序列，Walsh码具有良好的互相关性，不同的Walsh码是完全正交的，但是Walsh码有两个缺点，一方面是其自相关性能比较差，另外一方面是Walsh码的随机性较差［4］，所以对于同步捕获的性能也有一定影响，在标准MIL-STD-188-110C附录C中还采用到了Barker序列，Barker序列有很强的自相关特性，也是性能比较优良的伪随机码，但Barker序列本身长度太短，实际应用中受到限制［5］。

针对目前同步序列中存在的问题，本文基于混沌理论提出了一种新的同步序列生成方案。基于混沌映射分别设计了LC-C混沌序列和LC混沌序列，其中LC-C混沌序列用于生成同步序列集，LC混沌序列用于从同步序列集中抽取得到当前的同步头，由此可实现每次发送的同步头实时变化，不可预测，同步序列集的生成过程结合了优选策略保障了每次的同步头序列均有很好的相关特性和随机特性。对基于本方法生成的同步序列进行了仿真验证，并与m序列、gold序列以及标准MILSTD-188-110C附录C中的同步头进行了对比分析。

2 基于混沌理论的同步序列生成方法

同步序列的产生主要分为两个过程，即生成同步序列集的过程和从同步序列集每次动态变化选出同步头的过程，首先利用复合型混沌映射，将Logistic映射、Cubic映射和Chebyshev映射复合，所以可将该映射记为LC-C混沌映射，利用LC-C混沌映射生成LC-C混沌序列，然后经过优选策略得到的序列集合作为同步序列集，在进行优选时如果不满足优选条件，可以通过改变LC-C控制参数空间中的初值生成新的LC-C序列，其次利用级联型混沌映射，主要采用Logistic映射和Chebyshev映射级联生成，将该映射记为LC混沌映射，利用LC混沌映射生成LC混沌序列，将LC混沌序列输出映射成同步序列集的序列号，每次发送时利用LC混沌序列生成的序数从同步序列集中抽取得到当前发送的同步头，由于混沌映射的不可预测性，所以每次发送的同步头可实现实时变化，除此之外LC混沌序列采用和LC-C不同的混沌映射生成，进一步提高了同步序列的复杂度［6］，即使非合作方在破译LC-C混沌序列后，仍然无法得到当前准确的同步头。

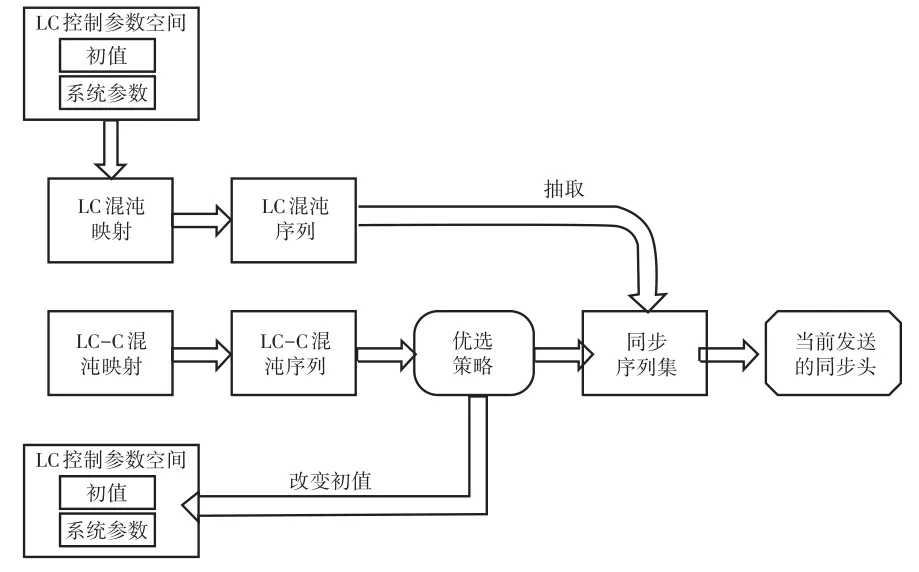
图1 同步头生成过程

2.1 LC-C混沌序列的生成

LC-C混沌序列采用复合型混沌映射生成，复合型混沌映射即采用多种映射方式复合，复杂度更高，可以有效降低被破译的风险［7］，本次设计中主要采用Logistic映射、Cubic映射、Chebyshev映射复合生成序列，所以记为LC-C混沌映射。由于Logistic映射和Cubic映射应用广泛且迭代方程相对简单［8］，所以作为第一级映射，Chebyshev映射平衡性较好，所以采用其作为第二级映射，确保输出序列平衡性优良，均值器主要将第一级输出的两者求平均，迭代n次，即第一级输出的长度为n的序列的每一项分别作为第二级的输入，第二级迭代n次，由此输出得到n个长度为n的序列，由于每个序列初值不同，所以每个序列都不相同。均值器的输出为

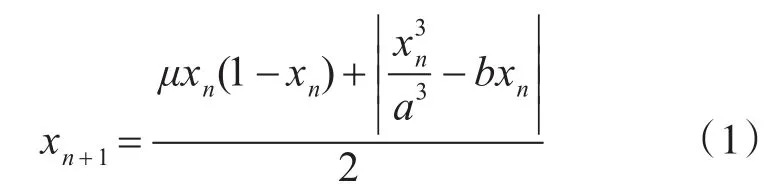
上式迭代n次得到的输出为{x1，}x2，x3，x4，…，xn，将该序列的每一项xn作为第二级Chebyshev的输入，第二级的映射方程为

所以LC混沌序列的输出为{y1，y2，y3，y4，…，yn}。

具体生成过程如图2所示。

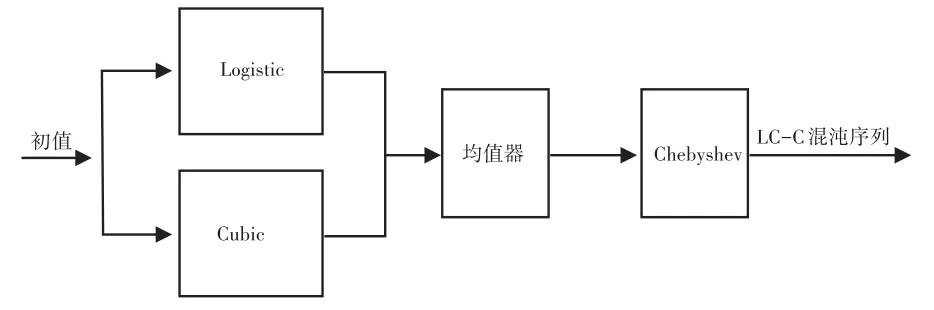
图2 LC-C混沌序列生成过程

2.2 优选策略

本设计中优选策略主要满足两个准则：平衡性准则和自相关准则。

1）平衡性准则

计算LC-C混沌序列的平衡度E，若E大于设定的阈值，则舍弃该序列。选取相同长度m序列的平衡度作为阈值。通过该优选准则的序列具有很好的平衡性［9］。

2）自相关准则

计算LC-C混沌序列的自相关旁瓣最大值和自相关旁瓣均方值，这两个值的大小会影响同步时相关峰的检测，两个值越小，同步性能越好，优选时若两者都小于设定的阈值，则通过该准则。选取相同长度m序列的自相关旁瓣最大值和自相关旁瓣均方值为阈值，通过该优选准则的序列具有很好的自相关特性。

2.3 LC混沌序列的生成

LC混沌序列采用级联型混沌映射，级联型混沌序列有效降低了被预测的可能性，同时提高了混沌系统的初值敏感性，所以级联型混沌序列是改善混沌系统复杂度和随机性能的简单有效方案［10］。本次设计采用的级联型混沌映射的第一级为常用的 Logistic映射［11～12］，第二级采用平衡性较好，迭代公式简单的Chebyshev映射，所以将该映射记为LC混沌映射，利用LC混沌映射生成LC混沌序列，首先将初值输入到映射，先经过Logistic映射，然后将Logistic的输出作为第二级Chebyshev的输入，整体迭代N次，得到长度为N的LC混沌序列，整体映射的迭代方程如下：

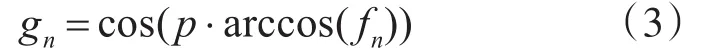
其中gn表示Chebyshev映射的输出，fn表示Logistic映射的输出，具体生成过程如图3所示。

图3 LC混沌序列生成过程

3 仿真分析

对基于本方法生成的同步序列的相关特性和随机特性进行了仿真，并与相同长度的m序列和Gold序列进行了对比分析，同时对同步序列随发送次数的变化情况和同步概率随门限值的变化情况也进行了仿真分析。

3.1 相关性和随机性分析

LC-C混沌序列的初值设为0.1～0.3之间，每次初值以0.001的间隔变化，最终得到的同步序列集大小为260个，与相同长度的m序列和Gold序列的自相关旁瓣最大值和自相关旁瓣均方值比较如图9所示。

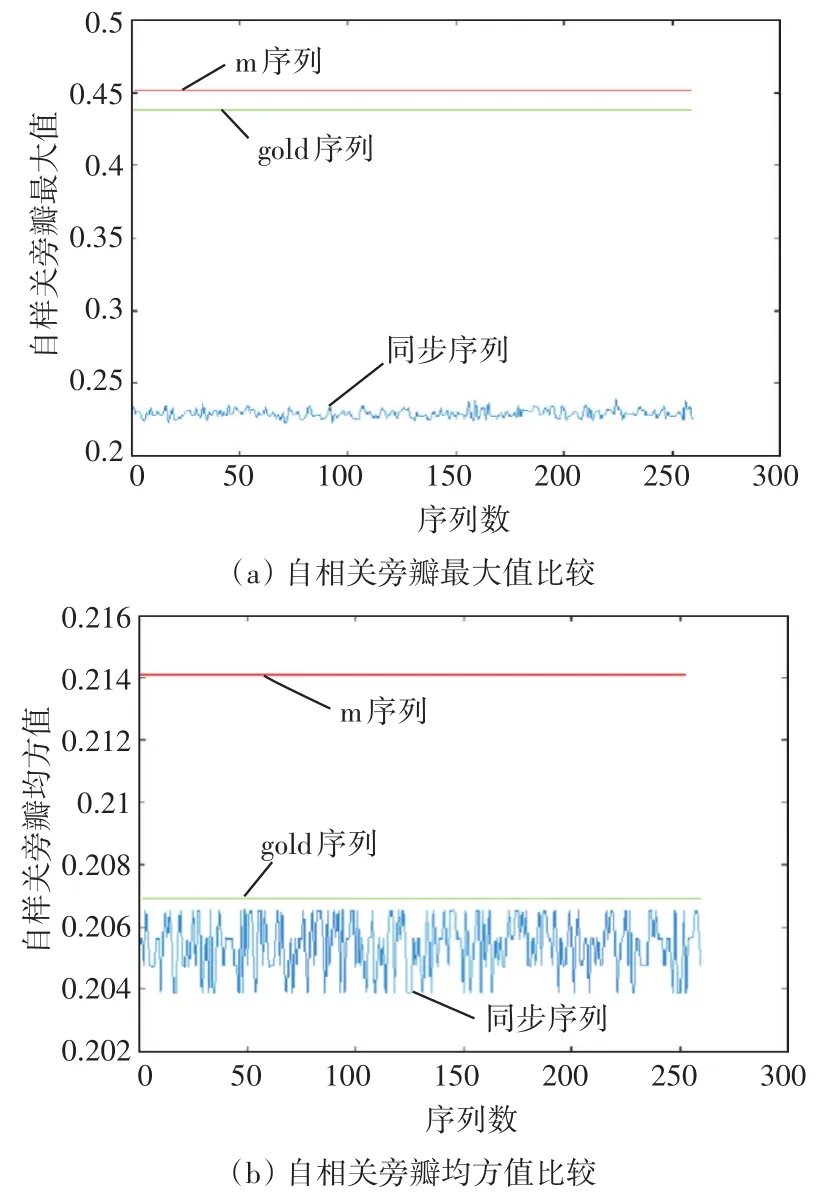
图4 与m序列和Gold序列的比较情况

随机抽取到的一个同步头的相关特性如图5所示。

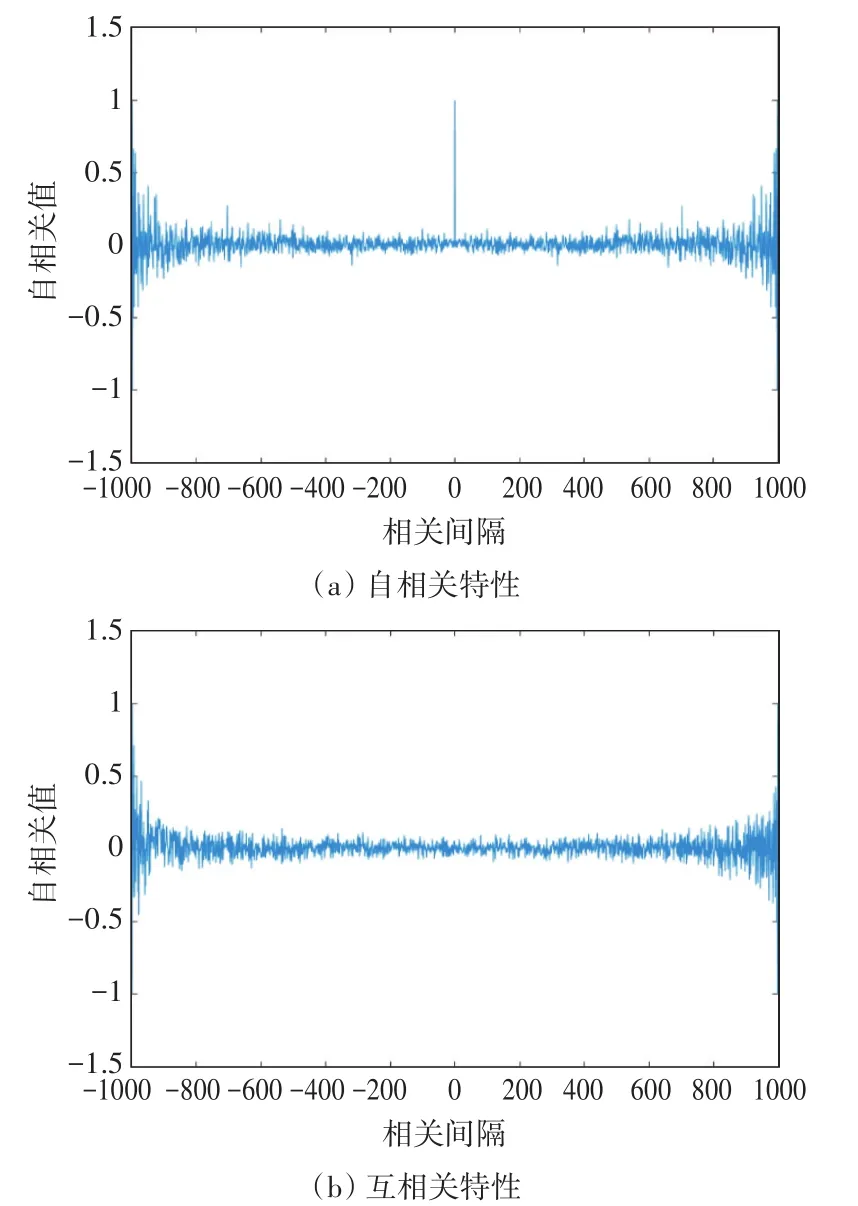
图5 同步头的自相关特性和互相关特性

根据上述结果可看出，本设计得出的同步序列具有尖锐的自相关性和良好的互相关性，自相关性能优于m序列、gold序列。

检测序列的随机性能需要借助NIST测试方法，以各项测试的p-value值作为序列的各项统计结果［13］，当其大于0.01时表示随机性良好，对于确定的系统而言，最主要的测试包括其频数测试、游程测试、谱测试和近似熵测试，将序列长度设置为10000，随机抽取出一个同步头进行测试，表1为测试结果。

表1 随机性测试

根据表1结果可知，结果值都大于0.01，说明同步序列完全通过了这几项测试，并且每项测试结果均较高，表明同步序列的随机性很好。

3.2 不可预测性分析

每次发送的同步头用相应编号代替，发送100次，每次发送时的同步头对应的编号如图6所示。

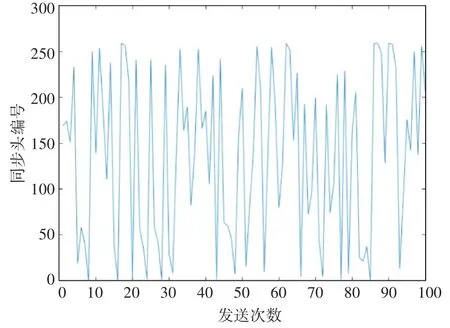
图6 同步头随机变化情况

根据图6可知，同步头编号随机变化，表明每次发送的同步头实时变化，不可预测。

3.3 同步概率分析

同步时需要借助门限值判断是否有信号到来，在相同信噪比条件下，同步概率会随着门限值的改变而变化，本文生成的同步序列和标准MIL-STD-188-110C附录C中的同步头的同步概率对比情况如图7所示。

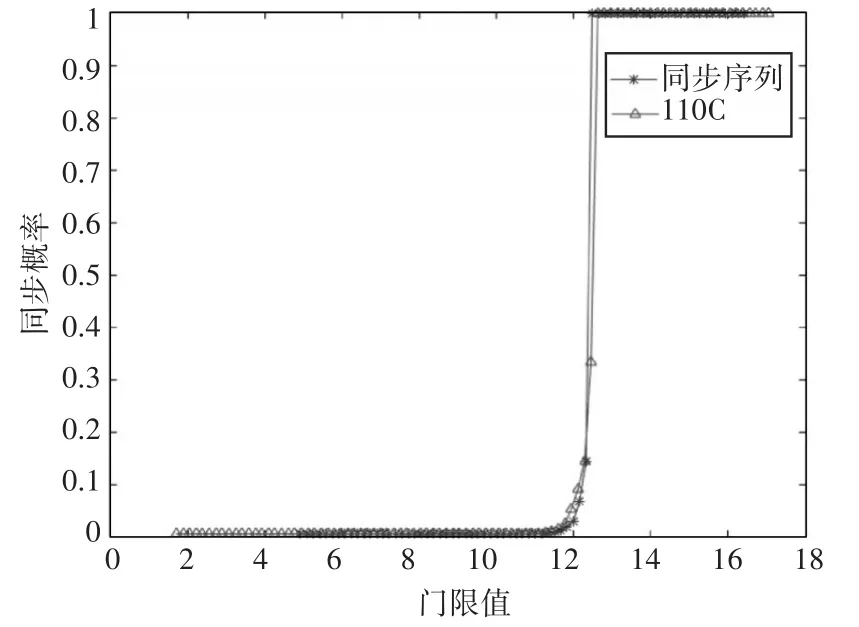
图7 同步概率对比图

根据图7可知，基于本方法生成的同步序列在门限值为12.48时同步概率达到100%，标准MIL-STD-188-110C附录C中的同步头在门限值为12.62时同步概率达到100%，本方法生成的同步序列同步性能略优于标准MIL-STD-188-110C附录C中的同步头。

通过仿真结果可以得出：本文提出的基于混沌理论生成的同步序列随发送次数实时变化，不可预测，每次发送的同步序列具有尖锐的自相关性，良好的互相关性和随机性，自相关性能优于m序列和Gold序列，同步性能略优于标准MIL-STD-188-110C附录C中的同步头。

4 结语

本文提出的基于混沌理论的同步序列生成方法利用多种混沌映射结合优选策略不仅能使每次发送时的同步头实时变化，且得到的同步头均具有很强的相关特性和随机特性。多种混沌映射的复合，使得生成的同步头具有较强的复杂度，同时同步头的实时变化也增强了同步序列的抗侦收能力，为解决现有同步序列容易被检测和截获的问题提供新的思路。