基于自适应滑动时间窗的四维航迹预测*

朱代武 刘 豪 黄邦菊 史继龙 陈泽晖

（1.中国民用航空飞行学院图书馆 广汉 618307）（2.中国民用航空飞行学院空中交通管理学院 广汉 618307）

1 引言

随着航空器数量的剧增，使得在其运行过程中出现空域资源紧张的问题，进而造成终端区和航路拥堵，为此美国和欧洲分别提出下一代空中交通管理系统-NextGen（Next Generation）和 SESAR（Single European Sky ATM Research）［1～3］。上述系统的核心皆是基于航迹的空域运行，即航行方式实现从基于传感器导航到基于性能导航的转变。同时航迹预测是辅助管制员决策的关键，因此航迹预测成为未来空管自动化决策的中坚力量。

目前对航迹预测主要采用以下两种方式：一是基于卡尔曼波的无参数估计。常用的是Lymperopoulos［4］等采用蒙特卡洛法简介对航迹进行评估及Wu［5］等采用的基于历史数据的多元线性回归法。二是基于航空器性能或气动学模型的方法。常见的是Warren等采用航空器运动方程，利用混杂系统递推求解航迹模型。但上述两种方法经常受到航空器机动性能多样性、大气环境及单一模型滤波的使用限制，因此本文提出基于自适应滑动时间窗的四维航迹预测方法，通过滑动时间窗估计下一时刻的状态矢量，进而提高航迹预测的精度。

2 预测模型

在航空器实际运行过程中，需通过ADS-B等雷达设备及时获取并进行状态评估：航班号、位置信息、运动状态及二次应答机编码。卡尔曼滤波是一个对动态序列进行线性最小方差估计的算法，适合用来解决目标状态跟踪及位置识别等问题［6～7］。其四维航迹预测模型的结构示意图如图1所示（Visio2015版）。

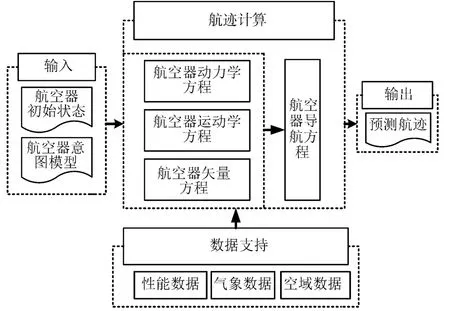
图1 四维航迹预测模型的结构示意图

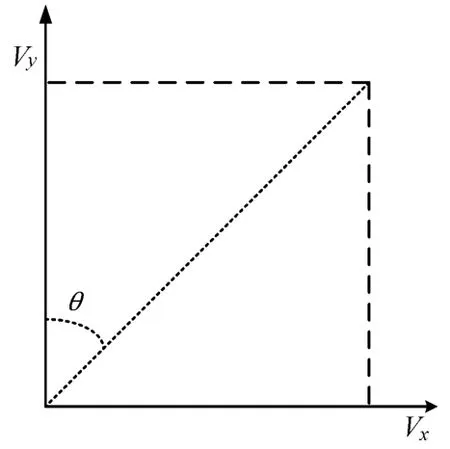
图2 航空器地速分解示意图

假设航空器的地速为V，航向为θ，对其进行速度分解为X轴的速度分量Vx，Y轴的速度分量为Vy即［8］：

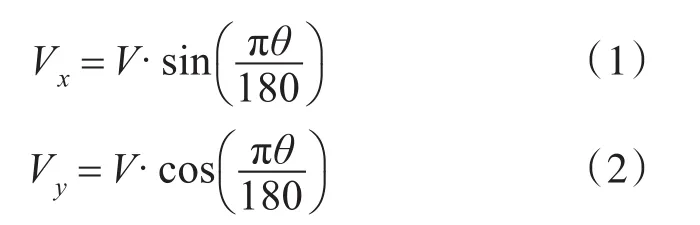
卡尔曼滤波根据系统的状态方程和观测方程，估计动态系统下一时刻的状态。即：

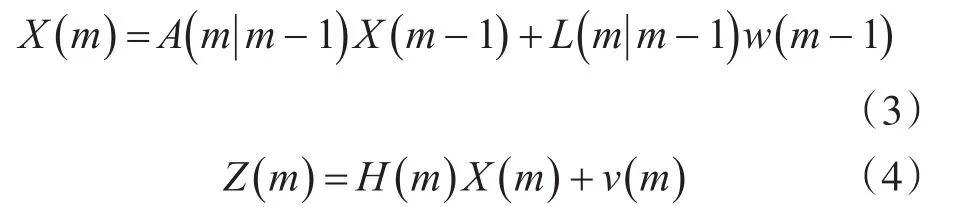
其中X（m）为系统状态矢量，表征在m时刻点的所有的运动向量；A（m|m-1）为描述目标体运动的状态转移方程；L（m|m-1）为干扰转移矩阵；w（m）表示运动模型的系统噪声，是p维零均值的白噪声限；Z（m）为所观测向量，描述m时刻的系统观测值；H（m）为所观测矩阵；v（m）为运动估计过程中所产生的噪声。

系统噪声w（m）与观测噪声v（m）相互独立存在的高斯噪声，其统计特性为

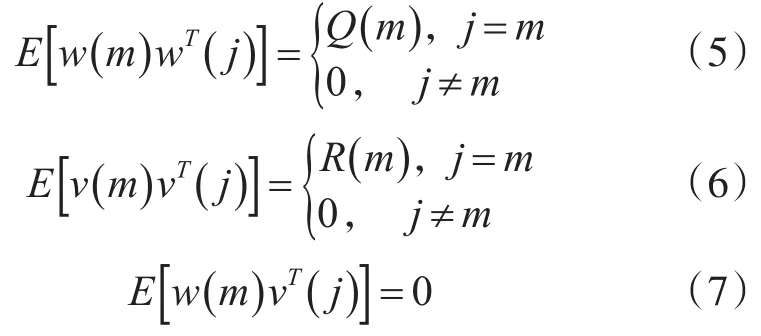
其中Q（m）是系统噪声w（m）的对称非负矩阵，R（m）为所观测到的总噪声v（m）的对称方差矩阵。

假设时间更新状态初始分布的均值和协方差矩阵分别为X0|0=X0和∑0|0=∑0，先验分布p（Xm|H0：m-1）在m时刻的均值和协方差定义为Xm|m-1和∑m|m-1，后验分布p（Xm|H0：m）在m时刻的均值和协方差定义为Xm|m和∑m|m［9］，其中先验分布和后验分布又被称为误差方差矩阵，可表示为P（m|m-1）。K（m）为滤波增益矩阵，对于m=1，…M，卡尔曼滤波可表示为时间更新和观测更新的动态方程［10］：

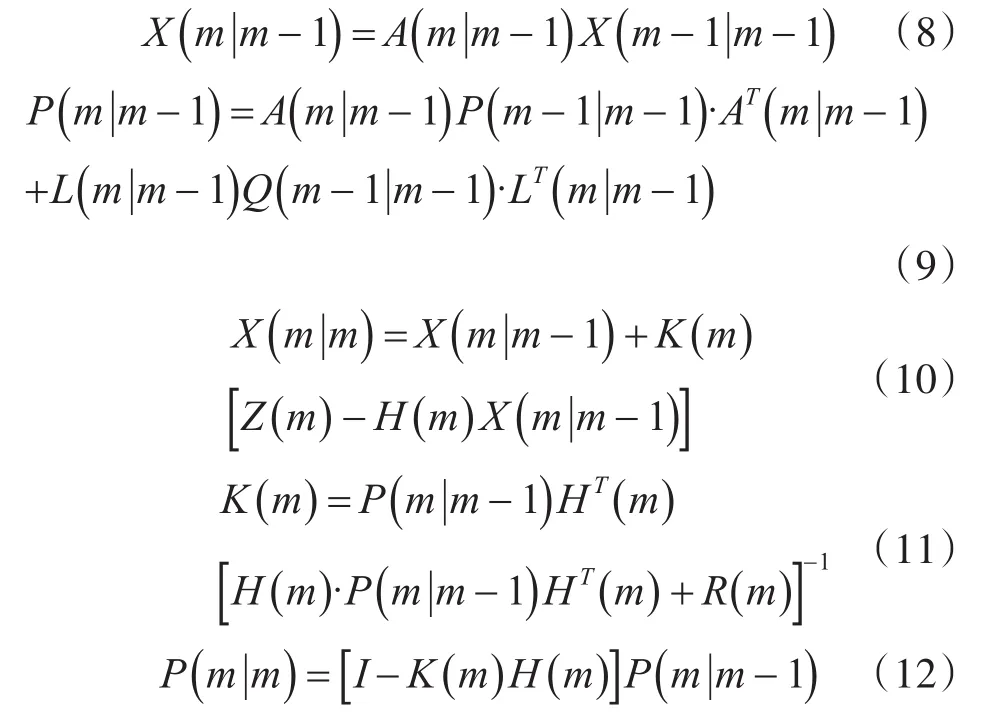
时间更新方程负责推进时间轴进而预测下一状态的矢量值和误差协方差估计值，为下一刻状态构建预评估模型；观测方程对其矢量及协方差估计偏差结合构造校验后的估计。根据时间和状态更新方程预测四维航迹从m-1时刻到m时刻的状态［10］。

3 滑动时间窗口构建

由于卡尔曼滤波本质上是将非线性问题线性处理，将会导致滤波单位精度的下降甚至分散。同时超前时间预测窗体过大会使预测精度降低，预测窗口过小航空器无法及时进行冲突识别及后续采取避让措施，因此根据飞机性能、航路环境建立自适应滑动窗体模型，对四维航迹进行高精度预测，其滑动模型如图3所示。

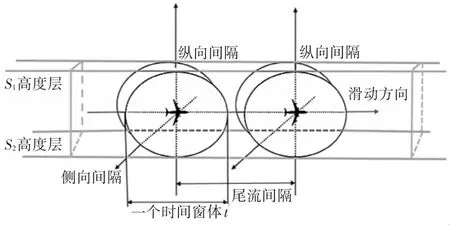
图3 自适应时间窗体滑动模型

滑动时间窗体可定义为当t为超前预测步数时，从当前时刻m到超前时刻m+t之间的滑动时间窗Tw=［Tm，Tm+t］［11］。通过找寻合适的预测时间窗体Tw即可求解超前预测步数t的过程，就移动目标与飞行冲突给出预测时间窗体的预测方法。

设ADS-B传感器的预测上限为tmax，超前预测步数应当满足t≤tmax。由卡尔曼可知加速度随机误差服从正态分布并且相互独立，即εk～N（0，δ2），速度与加速度的估计值为［vxm，vym，axm，aym］，以y方向的矢量为例，根据对应状态运动方程可得出：

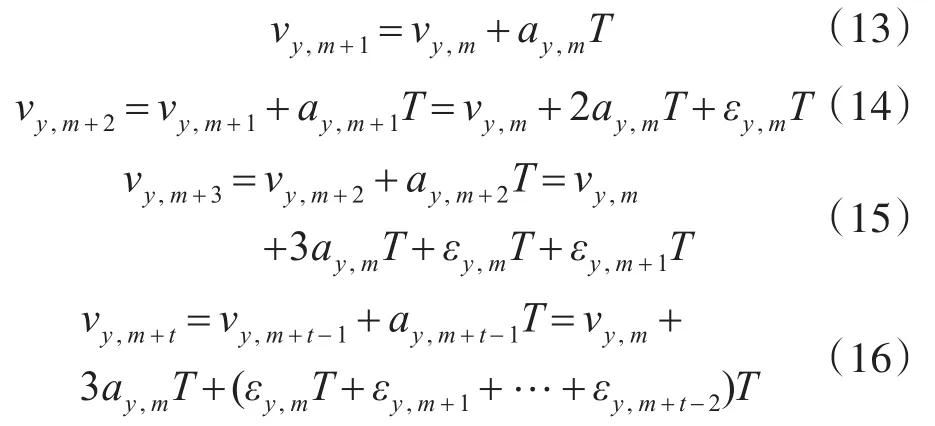
整理可得：

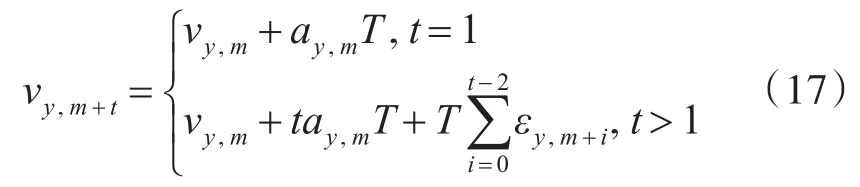
由正态分布的可累加性得：

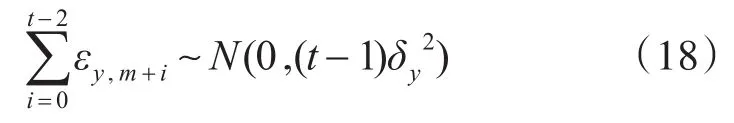
设uy，m+t为vy，m+t的估计值，利用［uxm，uym，axm，aym］进行航迹矢量信息预测，可知当t＞1时（对X方向同样适用），并可估算出航空器移动的平均速率u：

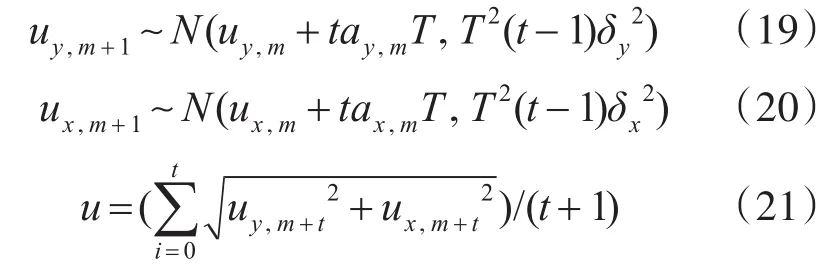
令t=tmax，并利用概率分布产生的随机矩阵即可得出滑动时间窗体内航空器的平均速率。同时采用自适应调整噪声协方差P（m|m-1）以减少外界干扰及信号丢失，引入自适应矩阵Gm，表述如下：

式中Sm=diag｛s1，s2，s3…sm｝，m为对应的航空器矢量维数，根据上述系统方程的定义及参数物理关系，可得状态转移的矩阵A（m|m-1）和观测矩阵H（m）。

假定航空器的飞行高度满足Hmin≤h≤hmax，根据航空器的机动性能及环境限制，可构造约束条件：

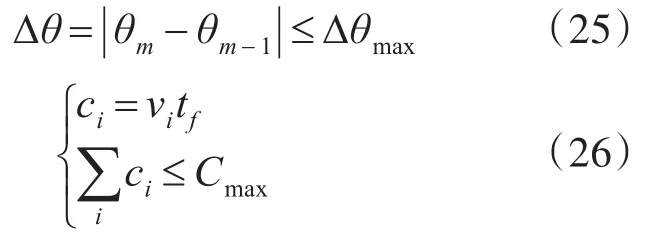
式中Δθ为航向改变角，由于航空器机动过载限制设其最大转角为Δθmax；tf为航空器相邻航迹点的飞行时间；cmin为最短的航迹段长度，即航空器在一个滑动时间窗体内的最小直线距离；cmax为最大航程。

4 仿真分析

以ZSNB-ZUUU航路为监测对象，以2018年7月份某航班CES9937（A320机型）的ADS-B实测数据为例，选取宁波栎社国际机场的ARP（机场基准点）作为空间坐标系的原点。部分A320数据如表1、表2所示。

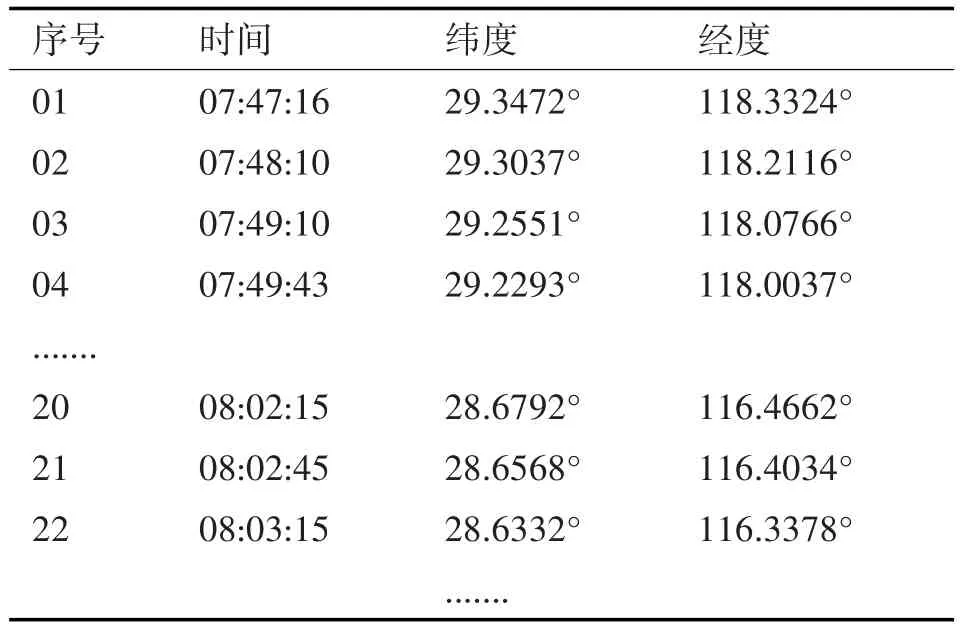
表1 CES9937航行时间位置图

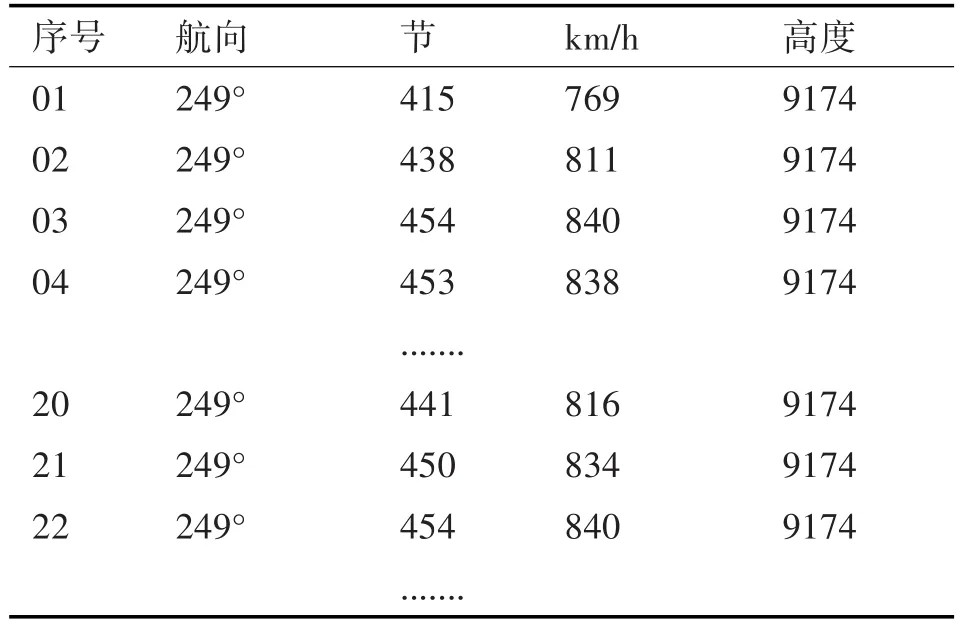
表2 CES9937航行速度高度图

在仿真实验中令采样周期控制在35±5s区间内，观测噪声R（n）=0.01×I4×4，Q（n）=I1×1，P（0|0）=8×I6×6，系统噪声参数为B（n|n-1）=0.01×I6×1，ADS-B扫描的等时间间隔为2s，因此航空器的航迹由离散的航迹点组成。航班CES9937的离场航迹及巡航航程实测航迹如图4所示。

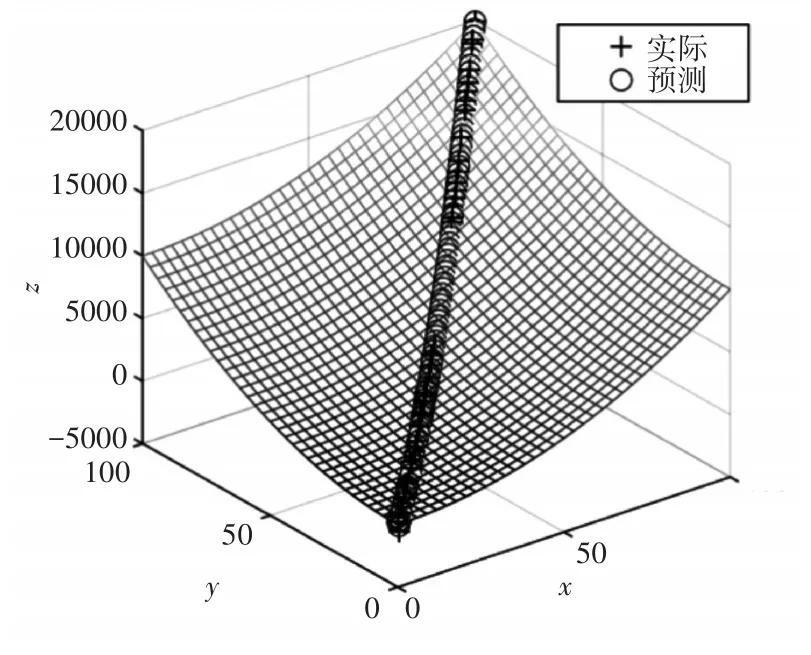
图4 CES9937航空器ZSNB离场图

从图4可知由于信号干扰、阻挡等因素会出现数据丢失问题，圆圈部分表示数据丢失，按时间间隔2s进行m元线性拟合。从图5可知CES9937航空器的真实值和观测值通过卡尔曼波曲线进行偏差分析，可知传统卡尔曼滤波预测方法对于四维航迹的预测误差较大。

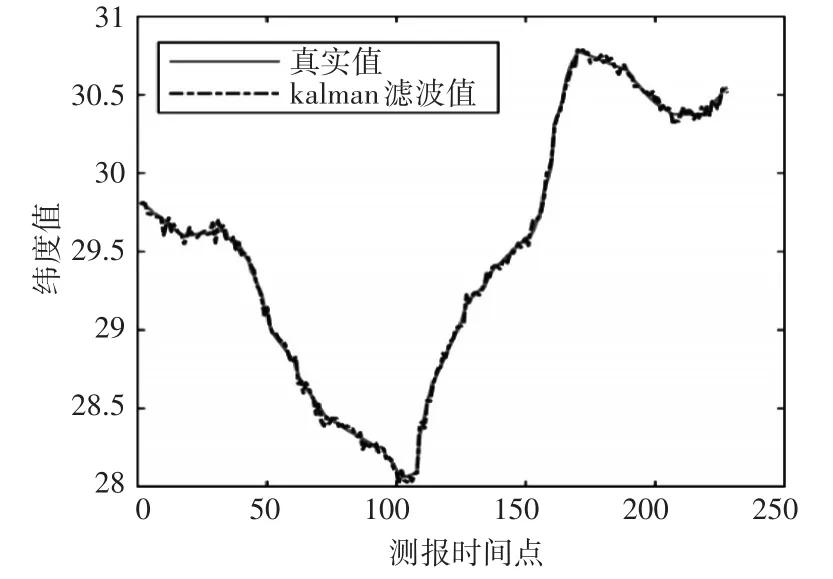
图5 CES9937航空器ZSNB-ZUUU航路图

采样周期T=2s，利用自适应滑动窗体模型的卡尔曼波并与传统的卡尔曼波的仿真结果进行仿真，通过利用机载传感器1，2对航空器运动测量的航迹及滤波预测结果进行偏差分析，其偏差如图6所示，同时对自适应滑动窗体模型与传统卡尔曼波X轴和Y轴的预测误差进行对比［12］。

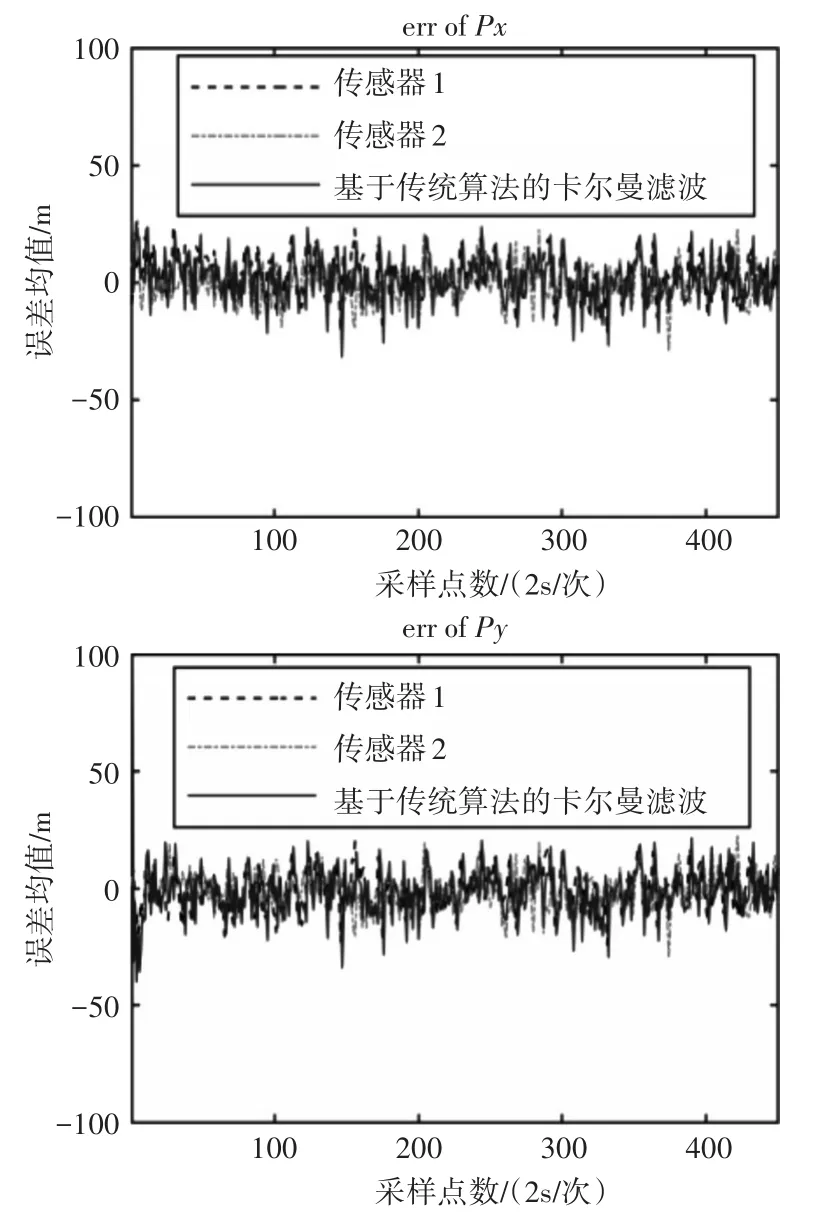
图6 基于传统算法的卡尔曼滤波

由图6、图7及图8可知当T=2s时，利用传统卡尔曼算法进行四维航迹预测时，X轴和Y轴的预测误差P（m|m-1）控制在±27m范围区间，而利用基于自适应滑动时间窗的卡尔曼滤波控制在±22m范围区间，对应误差如表3所示。

表3 传统卡尔曼与基于时间窗卡尔曼对比表

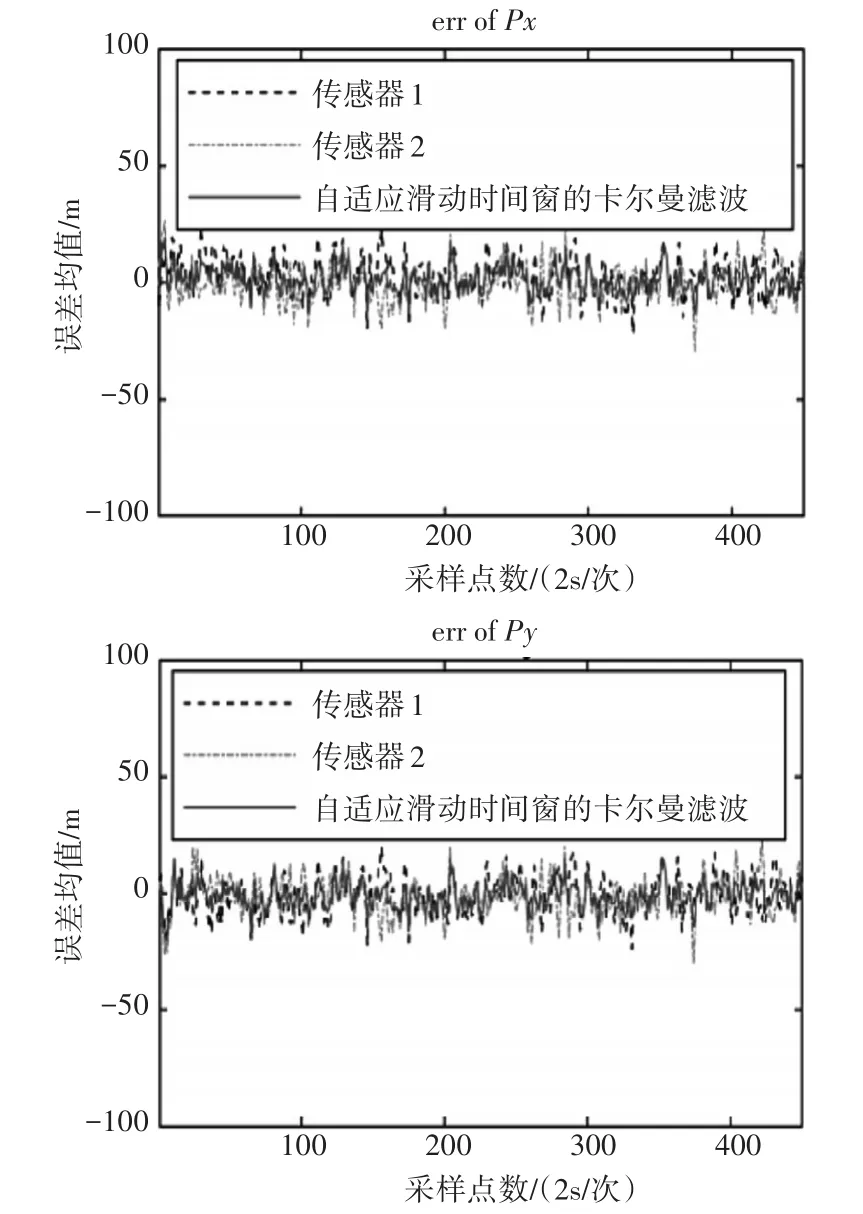
图7 基于自适应滑动时间窗的卡尔曼滤波

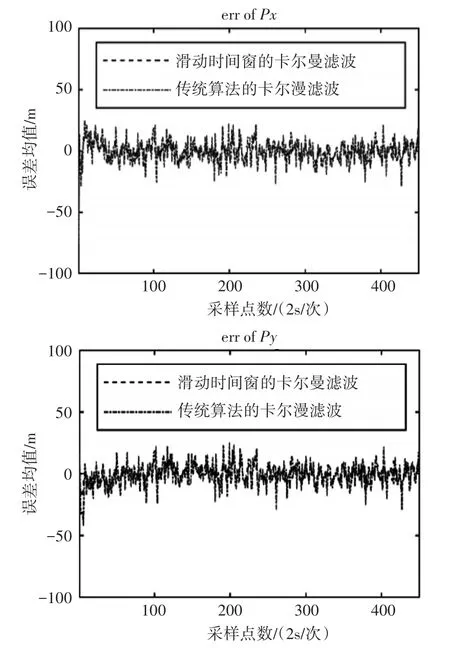
图8 传统卡尔曼滤波与自适应滑动时间窗的卡尔曼滤波对比

按照国际民航组织ICAO对航行通信要求，这里选取±50m作为导航基准源，区域概率和航迹的平滑性成正比，区域概率越大则误差越大，反之相反。通过对上述数据进行分析，可知传统卡尔曼滤波的区域概率为0.2916，基于滑动时间窗的卡尔曼滤波区域概率为0.1000，相比可知改进后的四维航迹区域误差减少65.8%，因此改进后的滤波发散性减弱，航迹的平滑性增强［10～13］，对应的滤波增益矩阵K（m）系数差异减小，按照实验数据对比为表4所示。

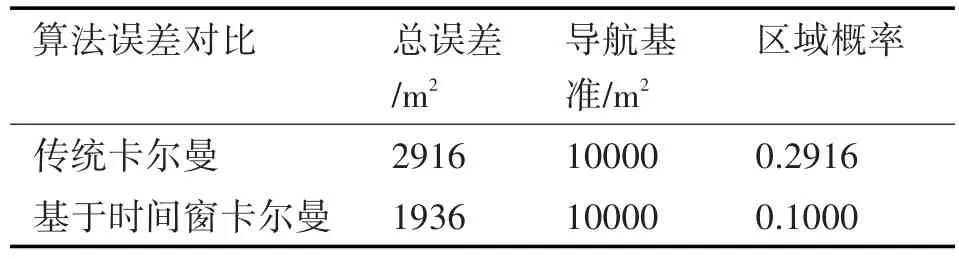
表4 传统卡尔曼与基于时间窗卡尔曼区域概率对比

以传统卡尔曼波区域概率0.2916为全误差基准，则改进后的误差概率缩减为原来的（0.2916-0.1000）/0.2916=0.658，对应误差缩减率具体如表5所示。

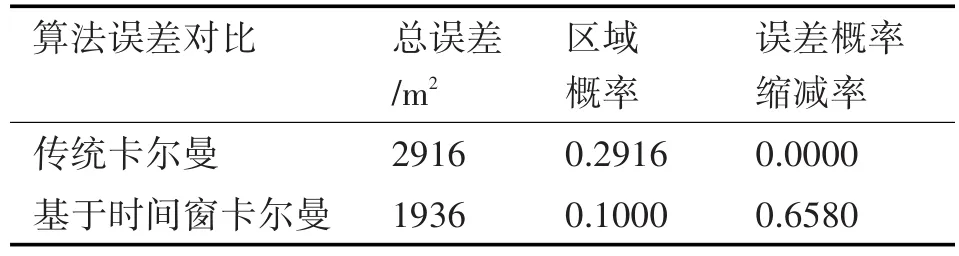
表5 传统卡尔曼与基于时间窗卡尔曼区域误差对比

由于航空器在实际飞行过程中，对地航向及速度收到航空器机动性能的影响不断变化，预测误差往往会上下波动偏置［14］，跟踪误差也必然存在波动偏置。通过观测上述图中的滤波，改进后的滑动时间窗能有效减少εk，在受到外界干扰的情况下其滤波性能够很快收敛，鲁棒性较好［15］。

5 结语

本文提出基于自适应滑动时间窗的四维航迹预测模型，解决了航空器四维航迹实时规划问题。通过对时间特性赋予的航空器机动进行评估［16］，引入自适应矩阵Gm保持卡尔曼滤波中的混合高斯模型适应外界干扰的多模态特点［17］，并在此基础上利用矢量因素及设定的误差矩阵P（m|m-1）求解实时四维航迹［18～20］。仿真结果证明基于自适应滑动时间窗的四维航迹预测模型是有效的，利用机载传感器及ADS-B数据能够实施精准四维航迹预测。