基于新型余弦组合窗相位差校正的介损角测量算法

李 宁, 迟长春, 郭振涛

(上海电机学院 电气学院, 上海 201306)

介损角是反映电气设备绝缘能力的重要指标,可以通过测量介损角间接掌握电气设备的绝缘性能[1]。目前,对介损角的测量一般有硬件测量法和软件测量法,而硬件测量法通常会受到环境因素的影响使得数据误差较大,故通常采用软件测量法,软件测量法中的谐波分析法[2-5]因其具有较高的稳定性和准确性而被广泛应用。非周期采样时因出现频谱泄露和栅栏效应[6-10]使电网信号的谐波分析法产生一定的偏差,影响最终介损角的测量结果。为使介损角测量更为精准,常用的方法是对电网信号加窗[11-13]处理,在这一方面,许多学者对不同窗函数进行了分析。李媛等[9]将Hanning窗和Nuttall组合,得到了旁瓣性能良好的组合窗函数。谢业强等[10]针对单个窗函数进行了自卷积,旁瓣性能得到了加强,但是增加了卷积运算计算量。王震等[11]对Hanning窗进行了改进,研究了3项Hanning窗函数,并推出双谱线插值公式,在一定程度上改善了频谱泄露能力,但是效果不明显,且双谱线插值相对三谱线插值计算精度不理想,计算过程相对繁杂。

本文提出了基于新型组合窗的介损角测量算法[14-16],利用Blackman-Harris窗以及Nuttall窗良好的旁瓣性能,构造了一种新型的Nuttall-Blackman-Harris余弦组合窗。在不同的实验环境下,通过与其他算法进行仿真分析对比,验证了该算法的可靠性。

1 介损角测量原理

图1为电容型器件的等效电路模型以及流入电流电压的向量图。其中,U为总电压;I为总电流;IC、IR为流过电容C和电阻R的电流;θ为功率因数角;δ为介质损耗角。

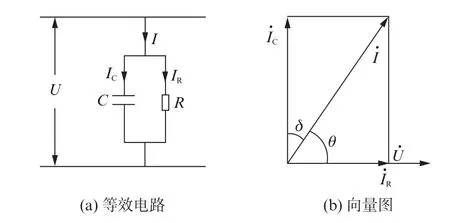
图1 并联等效电路和向量图

由图1(b)可见,绝缘介质损耗因数和介损角的值互余,由此得到绝缘介质损耗因数,估算出电气设备的绝缘性能。

图1中,设电路总电压和总电流为

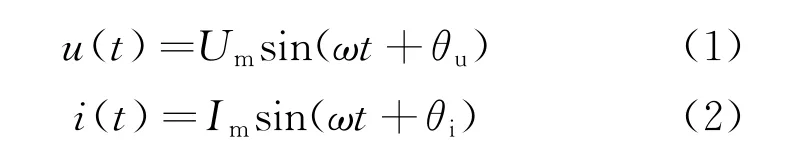
式中:Um为电压幅值;Im为电流幅值;ω为角频率;θu为电压初相位;θi为电流初相位。

式中:K为常数。

由式(5)可知,介质损耗功率与介损角成正比,故可直接通过测量介损角了解设备受损情况。介损角表达式为

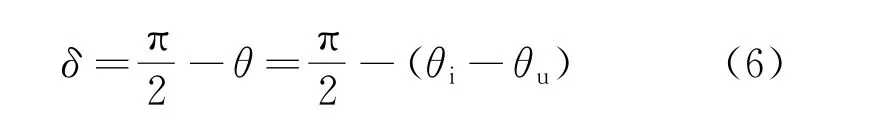
由式(6)可知,介损角的大小等于电压和基波电流初相位的差值。

2 新型Nuttall-Blackman-Harris余弦组合窗函数

2.1 Blackman-Harris窗函数

Blackman-Harris窗频谱简单,其旁瓣特性相比其他经典窗函数更好,时域表达式为

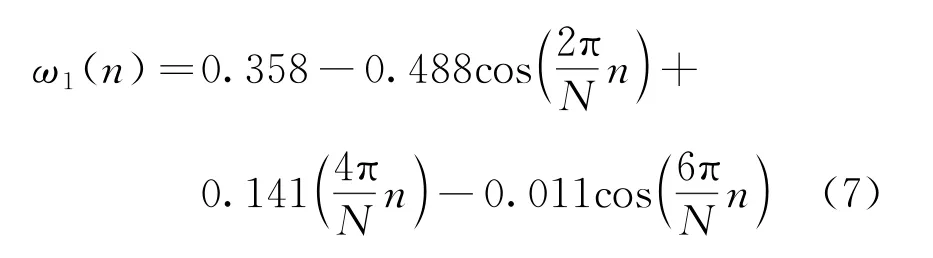
式中:N为窗函数的长度;n=0,1,…,N-1。

表1为5种常见的余弦窗函数旁瓣性能比较。由表可知,在经典窗函数中旁瓣峰值电平绝对值最大的是Blackman-Harris窗,且大幅度高于其他窗函数,虽然渐进衰减速率较低,但是窗函数的差距不是很大。整体上看,Blackman-Harris窗的旁瓣性能最佳。

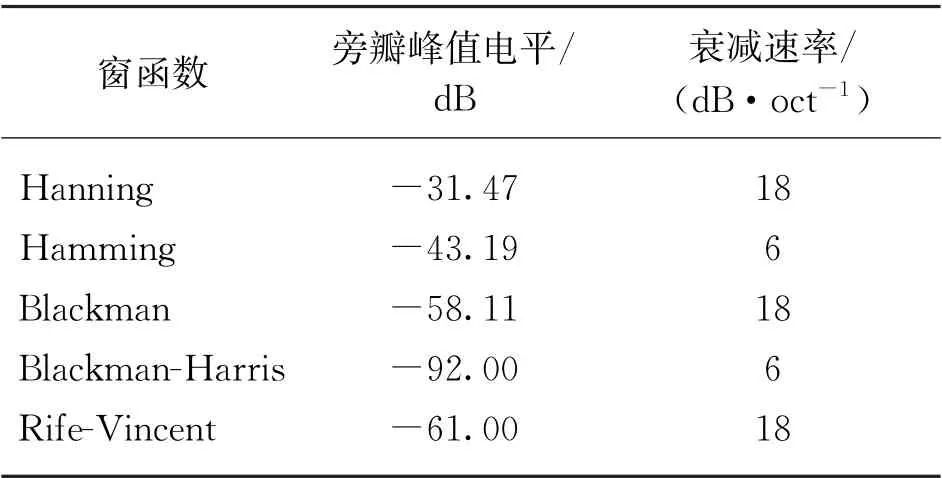
表1 经典窗函数的旁瓣特性

2.2 Nuttall窗函数

Nuttall窗是一种常见的余弦组合窗,其时域表达式为

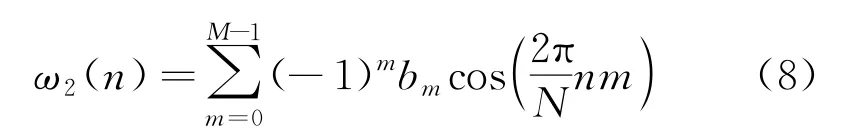
式中:M为窗函数的项数;n=0,1,…,N-1,N为窗函数的长度。

4种常见的Nuttall窗旁瓣峰值电平绝对值相差不大,均在-85 dB左右,而旁瓣衰减速率具有明显的差距,4项3阶Nuttall窗旁瓣衰减速率是4项1阶Nuttall窗的2倍,是3项最小旁瓣Nuttall窗和4项最小旁瓣Nuttall窗的5倍。因此,4项3阶Nuttall窗的旁瓣性能最佳。

2.3 Nuttall-Blackman-Harris窗的构造

Blackman-Harris窗和4阶3项Nuttall窗相比其他窗函数有更好的旁瓣特性,结合这两个窗的旁瓣性能特点,将Blackman-Harris窗和Nuttall窗组合,构造一个Nuttall-Blackman-Harris的新型窗函数。令Nuttall 窗函数的权重为β,Blackman-Harris窗的权重为λ,则新窗函数的时域表达式为

式(10)中β、λ二者之和为1,经过推导运算和仿真验证,当β=λ=0.5时该余弦组合窗的旁瓣性能最佳,其时域表达式为

由图2可知,新型组合窗函数表现出了很好的旁瓣特性,峰值电平达到了-104 dB,旁瓣衰减速率增加到了48 dB/oct,旁瓣性能相比Blackman-Harris窗和4阶3项Nuttall窗都得到了较大的提高,故抑制频谱泄露和栅栏效应的能力更强,使得δ的计算精度更高。

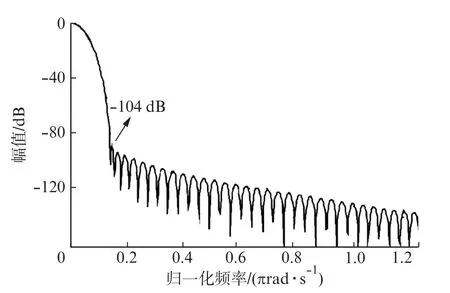
图2 Nuttall-Blackman-Harris余弦组合窗幅频响应

3 基于Nuttall-Blackman-Harris窗相位差校正的介损角测量方法

贲树俊等[14]对kaiser窗进行了卷积处理,提高了旁瓣性能,但是增大了计算量。本文采用运算更方便的相位差校正法测量介损角。

设电网信号中某一谐波分量为

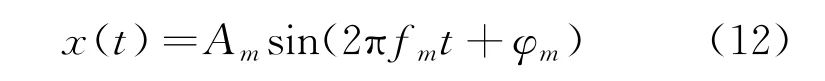
式中:m为基波或谐波次数;fm为基波或m次谐波频率;Am为基波或m次谐波幅值;φm为基波或m次谐波相位。

对该信号加Nuttall-Blackman-Harris 窗处理,加窗长度为N,通过傅里叶变换,有

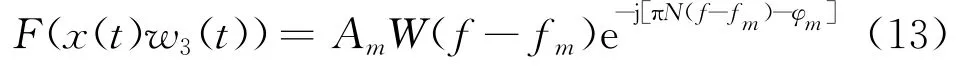
设采样频率为fs,以fs对x(t)采样,得离散序列为

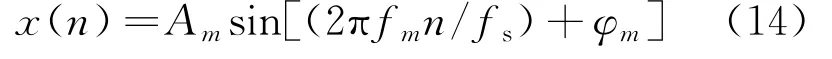
对离散序列进行截取,得到两个N点长的片段,其中两个片段之间平移的点数为L,将式(13)代入式(14),经傅里叶变换,可得离散频谱片段为

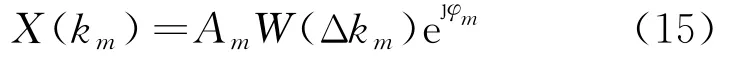
式中:km为第km条谱线;Δkm为第m次谐波的实际谱线与离散频谱中第km条谱线的位置差,即频偏

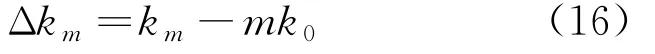
式中:k0为频谱中基波对应谱线;km=(fmN)/fs。

周期性采样时,有k1=k0=f0,但是一般情况下是非周期采样,所以Δkm≠0,m次谐波的实际频率fm=mf0,在频谱图中相应的谱线频率f'm=fskm/N,故频率误差可表示为

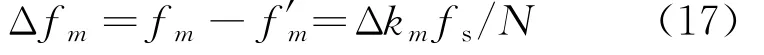
根据式(15)与式(16)可知,第km条谱线的相位可表示为

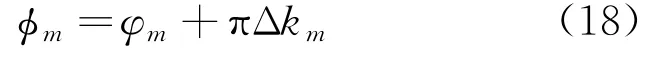
设第2个片段的离散频谱片段为X'(km),两个片段之间的长度为L,则第2个频段的频谱中,第km条谱线的相位为

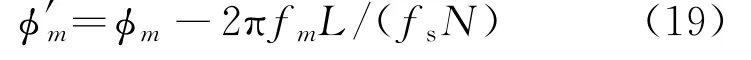
两个片段的相位差可表示为

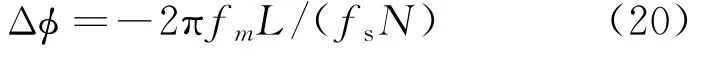
由式(17)和式(20)可推出频偏为

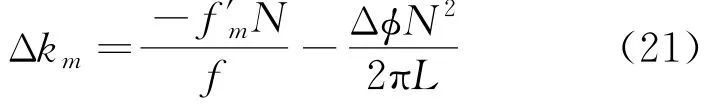
根据式(21)得校正的m次谐波相位为

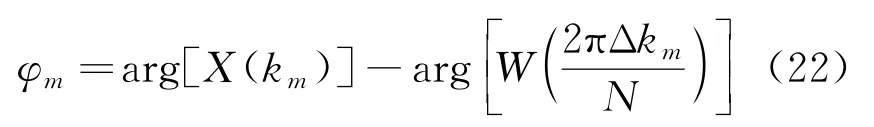
基于介损角的测量原理,通过式(22)可以得到基波信号的电压和电流初相位φu 和φi,此时m的值为1,求得的电压电流值代入式(6)即可求出介损角δ的值。

4 仿真分析

本文采用文献[17]中的电压模型和仿真电路,介损角仿真模型如图3所示,设含有谐波电流的电压信号为

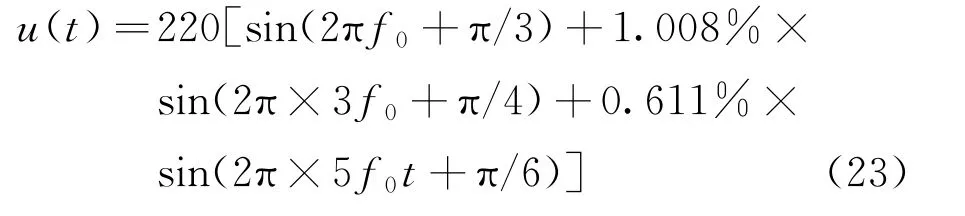
图3中,当电容值C=519.02 pF,R=22.67 kΩ,f0=50 Hz时,介损角的真实值δ=4.209 mrad。为验证本文算法的可靠性,在不同条件下对介损角进行测量,对比分析本文算法和其他经典算法的介损角测量相对误差。

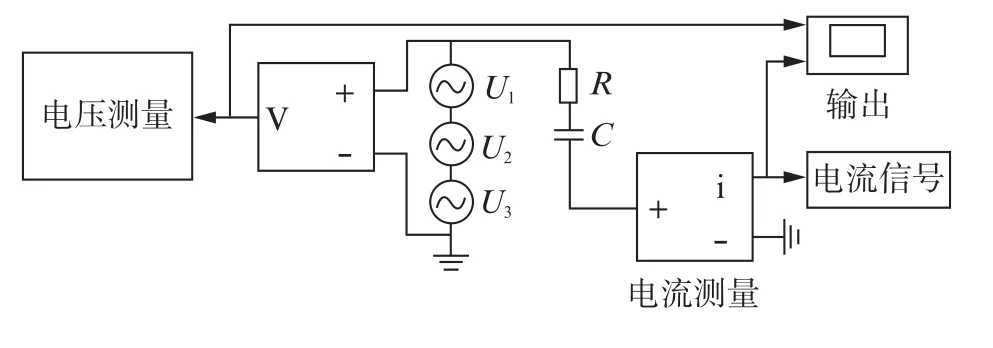
图3 介损角仿真模型

4.1 基波频率发生波动时对介损角测量的影响

取基波频率在49.5～50.5 Hz进行分析,通过基于4阶3项Nuttall窗、Blackman-Harris窗和Nuttall-Blackman-Harris窗相位差校正的介损角测量算法测量介损角δ。其中,采样频率为3 k Hz,采样点数为512,测量误差如图4所示。

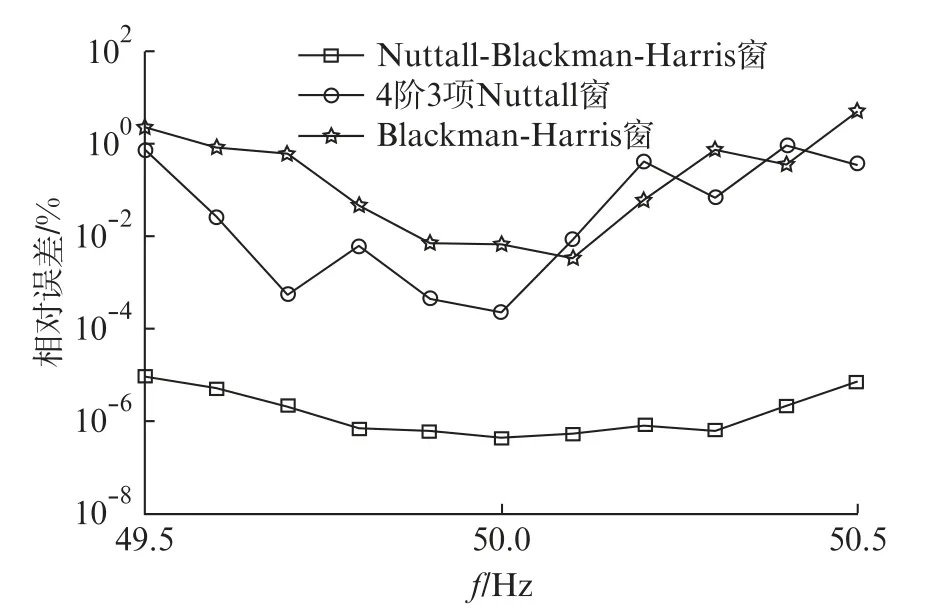
图4 频率波动对测量结果的影响

由图4可知,当条件相同的情况下,本文算法的相对误差比4项3阶Nuttall窗精确了4～5个数量级,比Blackman-Harris窗精确了5～6个数量级,并且本文算法在频率波动的情况下相对误差平稳,说明了该算法的稳定性良好,测量精度较高。

4.2 谐波注入对测量的影响

电网信号中必然会伴随着谐波的产生,而在这些谐波中3次谐波的占比最多,干扰也最大,因此分析3次谐波的不同占比对测量的影响,其中谐波占比从0增加到8%,基波频率为50 Hz,用基于4阶3项Nuttall窗、Blackman-Harris窗和Nuttall-Blackman-Harris窗相位差校正的快速傅里叶变换对信号分析,得到介损角测量相对误差如图5所示。由图5可知,在条件相同时,3个算法的测量误差都较小,但本文算法的介损角测量相对误差比4项3 阶Nuttall窗精确了3～4 个数量级,比Blackman-Harris窗精确了4～5个数量级,在谐波含量不断变化的情况下,本文算法测量结果依然保持稳定。

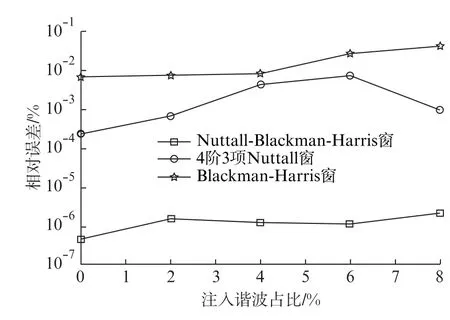
图5 谐波注入对测量结果的影响

4.3 白噪声对测量的影响

白噪声会影响介损角的测量,对信号加入白噪声,大小为10、30、50、70、90 dB,基于本文算法对介损角进行测量。考虑白噪声的特点,取100次测量结果求出平均值,并与测量误差最大值作比较,仿真结果如图6所示。

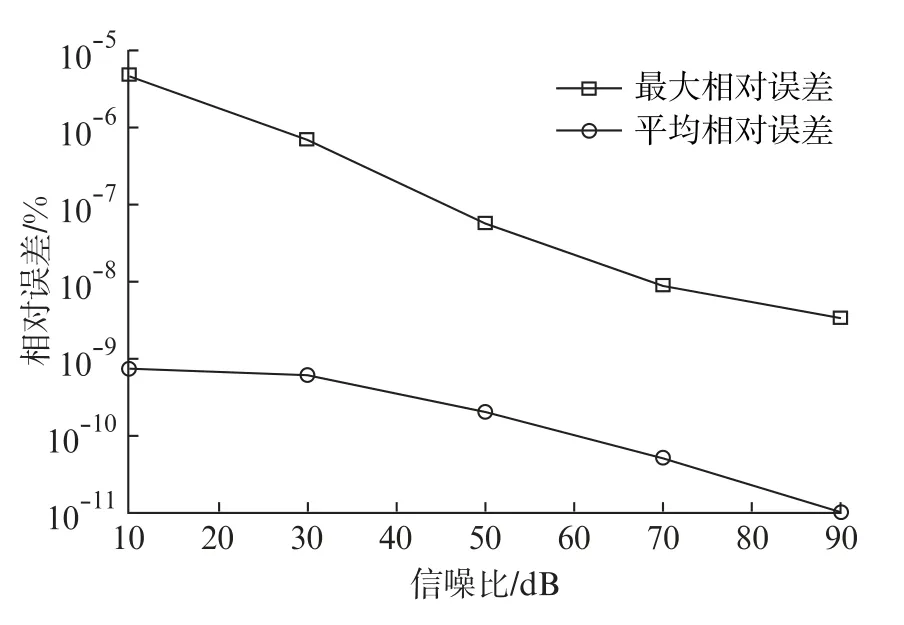
图6 信噪比对测量的影响

由图6可知,信噪比不断增大会导致介损角的测量误差越来越小,当信噪比不高于30 dB时,测量的相对误差较大,当信噪比大于50 dB时,测量平均相对误差精度在10-9的数量级,测量更准确,测量时取平均值能够较好地提高测量精度。

5 结 语

本文研究了Blackman-Harris窗与Nuttall窗的频谱特性,并构建了一个新型余弦组合窗,利用相位差校正算法,推导出基于新型组合窗相位差校正的介损角测量算法。在基波频率变化、注入不同比例谐波以及信噪比不同的条件下进行仿真实验,测量介损角的相对误差。结果表明:本文算法的稳定性好,测量精度高,抗干扰能力强,验证了本文算法的准确性与可靠性,为电气设备的绝缘性能检测提供了研究方向。