一种优化直流接触器电动斥力的改进方法

夏 林, 迟长春, 陈晋生

(上海电机学院 电气学院, 上海 201306)

随着可再生能源投入使用比例增加、电动汽车市场占比上升,人们对直流电气设备的需求逐步增加[1-3]。因此,直流接触器的安全性和可靠性越来越受到研究人员的关注。直流接触器导体回路的电动斥力由导体间的电动力和触点之间的霍尔姆力组成[4]。在短路电流故障下,电动斥力会使得触头回路断开。触头自动断开后产生的强大电弧会使触头表面熔化和汽化,最终导致触头材料或触头熔焊[5]。同时,直流接触器的突然断开也会影响电路中其他设备的运行。

对电动斥力的优化一直是电器领域的研究热点。国内学者对断路器、继电器的电动斥力及其影响因素做了大量研究[6-9],但是针对直流接触器电动斥力的研究很少。李兴文等[10]研究了长方形触头导电桥的位置对电动斥力的影响,但是没有分析圆形触头导电桥的位置对电动斥力的影响。对于电动斥力的优化,许多学者采用改变触头结构的方式[11-14]。董华军等[15]在真空灭弧室的触头之中添加不同形状的环形隔磁块DT4,有效地减小了触动间的电动斥力。陈晋生等[16]则通过添加方形隔磁块的方式优化电动斥力,但没有讨论隔磁块厚度对电动斥力的影响。

处在磁场中的隔磁块能够产生与该磁场相反的磁场,可以削弱磁场,进而减小电动斥力。本文将用于电动汽车充电桩、充电站领域的NDZ3T-400/750 V直流接触器作为研究对象,利用电磁仿真软件ANSYS对其触头系统在不同短路电流下产生的电动斥力进行研究。仿真结果发现,导电桥在不同位置时的电动斥力不同;当电流小于4 k A时选取厚度为1.5 mm 的方形隔磁块较为合适,当电流大于4 k A 则选择厚度为4 mm 的方形隔磁块;厚度相同的情况下,U 形隔磁块的优化效果要明显强于方形隔磁块。

1 触头系统电动斥力的数学模型和仿真

1.1 直流接触器的电动斥力

直流接触器可以通过控制线圈电流的通断,使得联动机构带动触头运动,进而控制电路的通断,其主要由动铁芯、静铁芯、线圈、动触头、静触头等组成,如图1所示。线圈通电后,动触头和静触头接触,当直流接触器控制的电路短路时,动触头、静触头以及动触板上的磁场强度会激增,进而导体回路的电动斥力也会大幅增加。在动触板上的平面上可以放置削弱磁场的隔磁块,从而降低电动斥力。

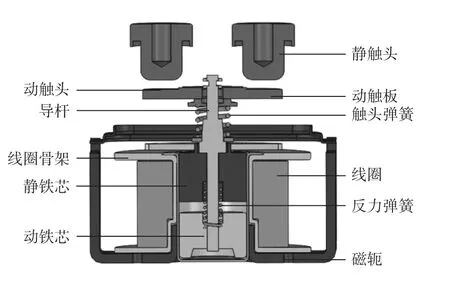
图1 直流接触器的结构

导体回路垂直方向的电动斥力FC由导体间的电动力FL和触点之间的霍尔姆力FH组成。工程上通常采用比奥 沙伐定理计算电动力。可将触头系统中的各个导体看作处于同一平面上,则电动力计算公式为

式中:μ0 为空气磁导率,μ0=4π×0.1μH/m;I为流过触头系统的电流;Kh为回路系数,与载流导体的长度、导体间的相互位置、导体间的介质有关,不同的情形下,回路系数会不同。

将触头机构的回路导体简化为两个互相平行的导体并垂直于另一条导体的结构。对于两个互相垂直的有限长载流导体,回路系数表达式为

式中:l为静触头长度;d为动触板长度;R为静触头的半径。

本文接触器l=115 mm,d=25.5 mm,R=5.5 mm,由于R≪l,则Kh简化为

简化的触头系统中电流流入的触头和动触板为互相垂直的两个导体,电流流出的触头和动触板也是互相垂直的两个导体,水平导体受到的总电动力为

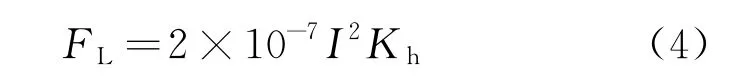
由于在触点附近,电流线收缩,上下两个触头之间会产生相反的电动力,简称为霍尔姆力。两对动静触头之间受到的霍尔姆力计算公式如下[17]:

式中:Fk为触头间的预压缩力;H为触头材料的布氏硬度;ξ为触头表面的粗糙程度,通常情况下取ξ=0.45。

通过公式求得r=0.26 mm。

1.2 隔磁块工作原理简介

隔磁块被磁化时,磁化强度表达式为

式中:Δv为磁化物质的微小单元的体积;Δm为微小部分中磁化电流的磁矩。

当隔磁块处于磁场H0之中时,会产生相应的附加磁场H′,其表示如下:

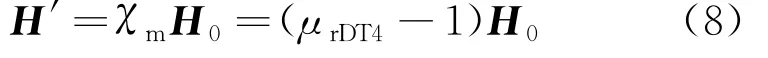
式中:χm为磁化率;μrDT4 为DT4的相对磁导率。

附加磁场的方向与外部磁场的方向相反,从而削弱了隔磁块附近的磁场。隔磁块周围的磁场表达式为

此时磁感应强度表达式为

式中:μr 为导电介质的相对磁导率。

利用隔磁块削弱触头系统的磁场强度,从而降低导体回路所受的电动斥力。通过改变隔磁块的厚度和形状,确定不同参数下的隔磁块对电动斥力的影响。

1.3 触头系统的有限元建模

在ANSYS软件中建立直流接触器的触头系统,模型如图2(a)所示,其中隔磁块放置在动触板的中间。对动静触头之间的导电桥单独建模,如图2(b)所示。假设导电桥是半径为r的圆形区域,R为静触头的半径。一般导电桥的厚度在0.10～0.25 mm,这里取厚度为0.15 mm[18]。

图2 触头系统模型及导电桥模型

设定该直流接触器的动静触头、导电桥等参与导电的材料为铜,放置在动触板上的隔磁块材料为DT4。模型搭建完成后,设置计算边界为零切线磁场强度场,并在触头表面施加短路电流激励。划分模型网格后,在动触板上设定求解参数,即动触板所受的电动斥力,求解后得到仿真结果。

2 仿真结果与分析

2.1 模型仿真计算验证

为了确保模型的可靠性,对直流接触器的触头系统在不同短路电流下的电流电动斥力进行理论计算,并与实际的有限元仿真结果对比,结果如图3所示。

图3 电动斥力(F)的理论值和仿真值对比

由图3可知,总体上看,理论值和仿真值的计算结果相近,当短路电流变大后,理论值和仿真值的差异逐渐增大,这是因为理论计算结果是根据接触器的触头系统简化后得来的,只能大致体现电动斥力的变化,而有限元则是对实际的触头系统进行建模,计算结果更加准确。

2.2 导电桥所在位置对电动斥力的影响

假设每个静触头上只存在一个导电桥,按照图4中位置1～7号分别放置,其中4号位置处于触头的圆心,剩余的位置沿X轴分布在距离4号±1 mm,±2.5 mm,±4 mm 的位置。由于市场上直流接触器的短时耐受电流最高为8 k A,故限定仿真中短路电流最高为8 k A。设置短路电流I=8 k A,则电动斥力的结果如表1所示。

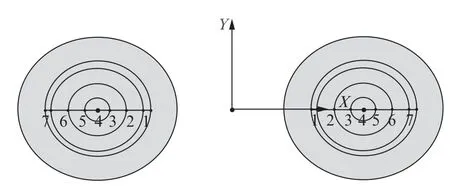
图4 导电桥位置分布

表1 不同位置导电桥的电动斥力

由表1可知,离动触板中心越近,触头系统的电动斥力就越小,反之越大。位置1的电动斥力最小,位置7的电动斥力最大。

2.3 不同位置下方形隔磁块对电动斥力的影响

将12 mm×12 mm×1 mm 的方形隔磁块放置在动触板上,隔磁块的中心和动触板的中心重合。设降幅比例的计算公式为

式中:FC为不放置隔磁块的电动斥力;F′C为放置隔磁块后的电动斥力。

电流为2、4、6和8 k A 时,仿真结果以及相应降幅比例计算如表2所示。

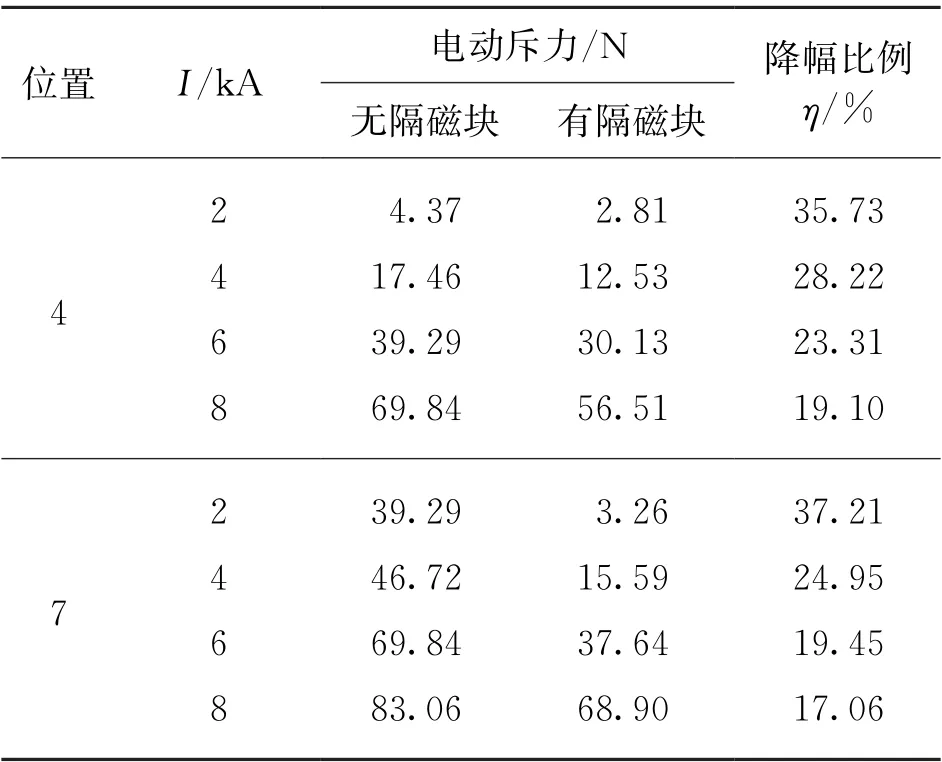
表2 不同位置下方形隔磁块对电动斥力的降幅比例

由表2可知,当导电桥处于位置4或者7时,方形隔磁块在不同的短路电流下都能一定程度上减小电动斥力。在相同短路电流下,不同位置的降幅比相差小于5%,且降幅趋势相同。因此,为了便于仿真,选择处于位置4的导电桥模型进行仿真。

2.4 不同厚度的隔磁块对电动斥力的影响

改变方形隔磁块厚度h从1.0～4.5 mm,间隔为0.5 mm,仿真数据如表3所示。由表可知,短路电流不变的情况下,随着隔磁块厚度的增加,电动斥力也有所下降,但是下降的趋势越来越平缓。考虑到触头的压力为30 N,当短路电流小于4 k A时,无论选择哪一种厚度的隔磁块都能减小电动斥力。

表3 不同厚度、不同电流下的方形隔磁块的电动斥力

设降幅变化率为

式中:ηh-为没有增加0.5 mm 隔磁块时对应的电动斥力降幅比例;ηh 为当前隔磁块厚度下的电动斥力降幅比例。

特别地,当h=1 mm 时,取Δη=ηh,对应的电动斥力降幅变化率曲线如图5所示。

图5 不同厚度的方形隔磁块的电动斥力降幅变化率

由图5可知,当短路电流小于4 k A时,厚度大于1.5 mm 的隔磁块降幅的效果趋于平缓,即隔磁块的厚度再增加也不会有明显的电动斥力优化效果,故选择厚度为1.5 mm 的隔磁块较为合适。同理,当短路电流大于4 k A 时,隔磁块越厚,电动斥力越小,但是当厚度达到4 mm 后,电动斥力下降的趋势越来越平缓。因此,当短路电流大于4 k A时,选择厚度为4 mm 的隔磁块较为合适。

2.5 U形隔磁块对电动斥力的影响

为了解决方形隔磁块随着厚度增加,电动斥力不再明显的问题,对隔磁块进行改造。由于动触板中心的磁场强度相对较小,而越靠近动触板边缘以及导电桥的位置时,磁场强度越大。根据动触板磁场强度的分布,设计U 型隔磁块,如图6所示,覆盖动触板的边缘。

图6 U形隔磁块摆放示意图

确定短路电流小于4 k A、厚度h=1.5 mm 与短路电流大于4 k A、厚度h=4 mm 的U 型隔磁块对电动斥力的仿真效果,仿真结果如表4所示。

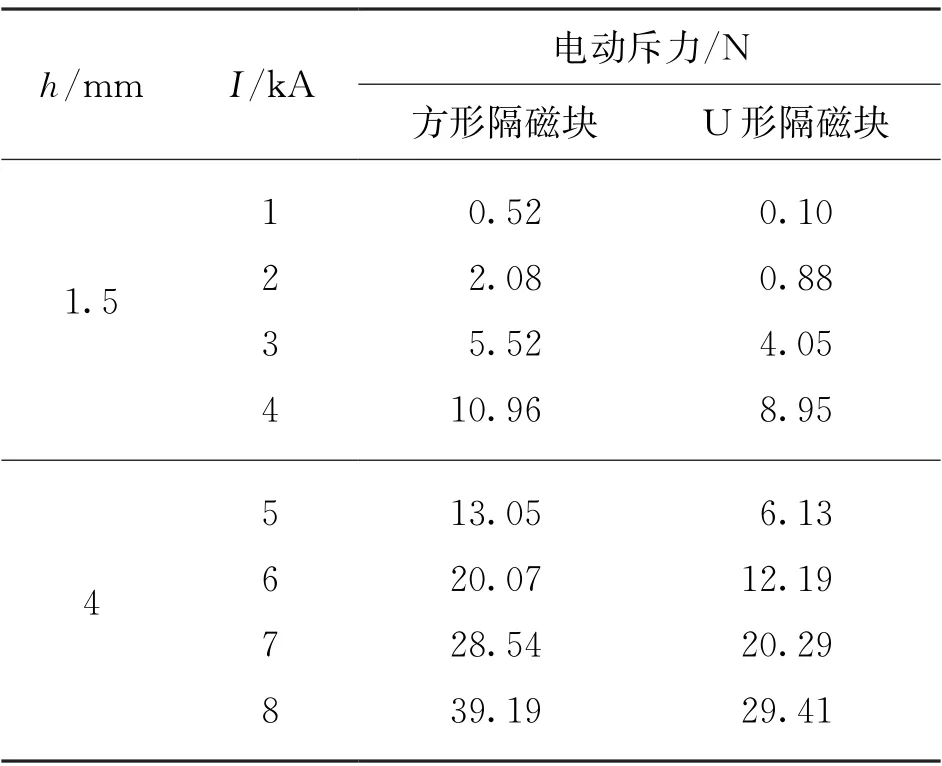
表4 不同条件下方形隔磁块和U形隔磁块的电动斥力

结合图3中的仿真值,计算方形隔磁块和U形隔磁块在不同条件下对电动斥力的降幅比例,计算结果如图7所示。

图7 不同厚度下方形和U形隔磁块的降幅比例

由图7可知,当电流小于4 k A 时,1.5 mm 的U 型隔磁块的优化效果比1.5 mm 的方形隔磁块更优,并且U 型隔磁块的降幅比例至少比方形隔磁块的降幅比例多11.51%;当电流大于4 k A 时,4 mm 的U 型隔磁块的优化效果要强于4 mm 的方形隔磁块,并且U 型隔磁块的降幅比例至少比方形隔磁块的降幅比例多14.01%。

3 结 语

本文对直流接触器的触头系统进行了仿真,在ANSYS之中建立触头系统的Maxwell 3D 模型。改变了静触头上导电桥的位置,发现导电桥离动触板中心越远,触头系统的电动斥力就越强。当短路电流小于4 k A 时,选择厚度为1.5 mm 的方形隔磁块可以取得较好的电动斥力优化效果;当短路电流大于4 k A 时,则选择厚度为4 mm 的方形隔磁块。在隔磁块厚度相同,短路电流相同的条件下,U 形隔磁块的优化效果要强于方形隔磁块,且电动斥力的降幅比例至少比方形隔磁块的降幅比例多10%。本文通过研究隔磁块厚度和形状,提高了直流接触器的短时电流耐受能力,增强了直流接触器在短路电路下的安全性和可靠性,为后续相同类型更大容量的直流接触器的电动力稳定性优化研究提供了参考依据。