基于IACS-IGA 的分布式电源配置结构优化

李 磊, 高桂革

(上海电机学院 电气学院, 上海 201306)

随着智能时代的开启,人们逐渐重视分布式电源(Distributed Generation,DG)与电力网连接的相关问题。由于DG的随机性和间歇性很强,大量并网会改变电力网的原始结构,影响其稳定性。DG接入电力网的位置和容量不同,会对电力系统的电压稳定性、网络损失和潮流流向产生重大的影响[1-3]。因此,合理地规划分布式电源接入位置和容量对降低电力网的有功功率网络损失、降低电压偏差,以及提高电网的安全性、经济性、稳定性的意义非凡。但是,DG的设置位置和容量配置不合理时,电力系统也会有很大的负担。现在,有很多学者从不同角度研究DG 的优化结构配置问题。文献[4]将蒙特卡罗准则引入天牛须算法,以网络损耗、电压和电流稳定性为目标函数,大幅提高了算法的稳定性,但该算法的收敛性仍然很差,重复次数太多。文献[5]是隐含编码的遗传算法,以综合投资费用的最小化为目标函数,但需要计算DG的数量和访问位置,增加了计算量。在文献[6]中,DG采用融合模拟退火的遗传算法进行配置结构优化,虽然提高了算法的全局搜索能力,但是在收敛速度和精度方面未能达到理想效果。文献[7]考虑一些无法预测的因素会导致负荷和输出功率的不确定性,采用机会约束规划的办法进行无功优化,但由于目标解之间的冲突,所以结果并不理想。利用上述文献进行DG的配置结构优化计算时,都不能达到理想的效果,DG 的位置和容量优化规划的问题不能得到很好的解决。

本文以综合投资费用最小为目标,建立DG选址配置的优化模型。将改进自适应布谷鸟搜索(Improved Adaptive Cuckoo Search,IACS)算法中的莱维飞行策略和淘汰机制引入遗传算法(Genetic Algorithm,GA)中,形成了改进的自适应布谷鸟 遗传算法(Improved Adaptive Cuckoo Search-Improved Genetic Algorithm,IACS-IGA)。在Matlab2018b平台上进行仿真分析,证明该混合算法能够很好地解决分布式电源的配置结构优化问题,并且收敛性优于单一算法。

1 构建DG优化结构配置模型

1.1 目标函数

配电网相关问题的求解往往涉及非线性和多目标性,可根据实际需求选择不同的目标函数。本文以建立最小化的DG综合投资费用模型为目标。综合投资费用包括发电费用、网络损失费用、DG环境保护费用。最小综合投资费用为

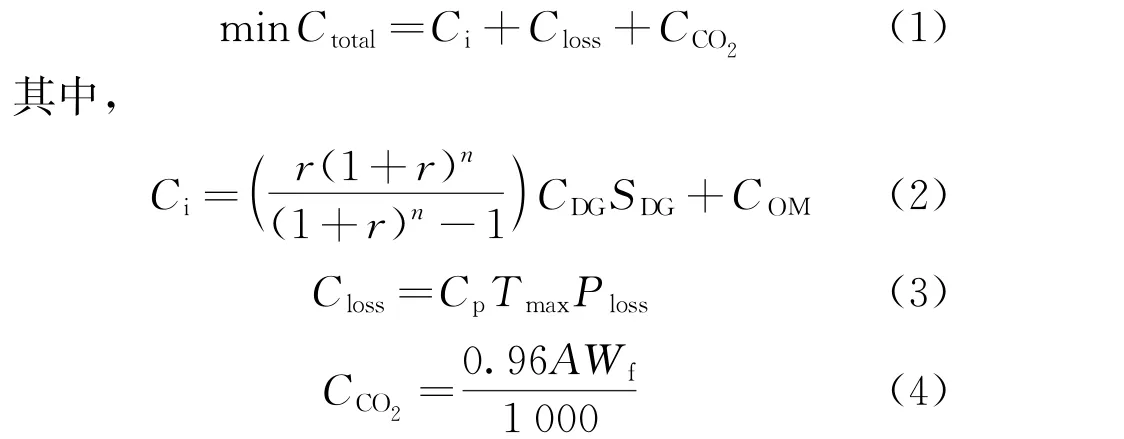
式中:Ci为DG 平均每年的发电费用,元;Closs为配电网的线路损耗费用,元;CCO2为配电网二氧化碳排放费用,元;r为平均每年的回报率;n为使用期限,a;CDG为单位容量DG的投资费用,取1 500元/kW;SDG为安装DG的总容量,kW;COM为DG的运行费用,取500元/kW;Cp为电费,元/kWh;Tmax为年最大利用负荷时间,h;Ploss为线路的有功损耗,kW;A为环境惩罚系数,取0.97元/t;Wf为发电量,kWh。

1.2 约束条件

(1)节点电压约束表达式为

式中:PGi为节点i注入的有功功率;QGi为节点i注入的无功功率;PDGi为第i节点上DG的有功功率;QDGi为第i节点上DG无功功率;PLi为节点i中注入负荷的有功功率;QLi为节点i中注入负荷的无功功率;Ui和Uj分别为节点i、j的电压;Gij、Bij为节点i、j之间的电导和电纳;φij为功率因数角。

本文采用极坐标形式下的牛顿拉夫逊法潮流计算功率、电压分布和有功损耗,使用前推回代法计算各支路的潮流损耗[8]。通过对雅可比矩阵进行简化,保证求解的速度与精度。

2 IACS-IGA算法分析

2.1 改进的自适应布谷鸟搜索算法

布谷鸟搜索(Cuckoo Search,CS)算法具有搜索路径能力优秀、搜索能力强、参数少等特点[9-11]。同时,CS算法能够利用莱维飞行(lêvy flight)的特征,有效地防止早熟现象。CS算法通过莱维飞行的方式来探索鸟窝的途径和更新位置,其表达式为[12]

通常,自适应布谷鸟搜索(Adaptive Cuckoo Search,ACS)算法只注重改进搜索步长,对于发现概率Pa往往只取常数。这样做不利于保持CS算法中全局和局部之间的平衡。为了解决此类问题,本文提出了一种IACS算法。通过在ACS算法中[12-13]引入动态发现概率,来自适应调整局部和整体的制约关系,保持算法的稳定性,其发现概率调整为

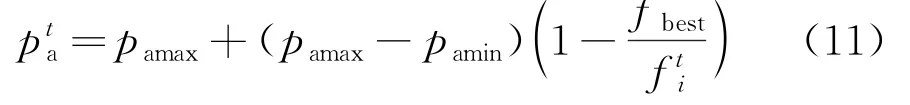
2.2 IACS-IGA算法的步骤

DG的优化中存在许多次级最优解,是典型的非线性多峰值问题。为了提高算法解的精度和收敛速度,同时提高算法跳出局部最优的能力,本文将改进交叉概率和变异概率的传统遗传算法(IGA)中引入CS 算法的淘汰机制和莱维飞行策略。

改进的目的:通过淘汰机制筛选出更优粒子的同时,提高算法的全局搜索能力;通过对交叉变异后的粒子进行莱维飞行寻优更新,加强后期局部收敛能力,形成了比其他算法[13-16]融合度更高的IACSIGA算法。定义N个个体{Xi,i=1,2,…,N},D维向量,即任意个体Xi={xi1,xi2,…,xiD}。

算法的不等式处理:通过分布式电源容量大小来约束Xi的上下边界。如果规划容量过大使得线路功率超载,则使用约束条件限制分布式容量为最大容量。对于在潮流计算中越限的电压变量,直接选择跳出潮流循环并舍弃当前粒子。IACSIGA混合算法形成的具体过程如下:

步骤1 种群编码。采用整数编码作为个体的基因值,基因值是相应DG容量的标幺值。设置种群个体数N=100,lêvy飞行自变量边界êmax=82.56,Xmin=0。

步骤2 初始化参数。初始化鸟窝位置的适应度值、初始化第1 代个体中各个元素,X1={x11,x12,…,x1D}。

步骤3 迭代。迭代条件为Whilet＜Nmax或其他终止条件。Nmax为最大迭代次数。

步骤4 筛选。通过式(11)得到的Pta淘汰旧鸟巢建立新鸟巢,筛选出适应度较低的鸟窝位置。

步骤5 选择。通过用轮盘赌的方法选择适应度高的鸟窝位置进行优先复制,适应度低的则被淘汰。

步骤6 交叉。本文采用双切点交叉,在个体编码中随机选取2个交叉点,交换后重组成子代个体,交叉率PC=0.4。

步骤7 变异。按照变异率随机改变基因位上的基因值,变异率PM=0.01。

步骤8 更新。利用莱维飞行公式,即式(9)和(10)更新当代鸟窝位置,选择适应度比上一代更优的鸟窝位置。

步骤9 迭代终止条件。当算法迭代次数大于或等于Nmax,或函数的适应度值精度满足要求时,程序结束,输出最优解。否则返回步骤3。

3 仿真验证

使用IEEE-33节点计算示例,系统的参考容量为10 MVA,负载总容量为4 369.65 k VA,总有功无功功率分别为3 175 k W 和2 300 kvar。接入系统的DG 总容量不超过系统负载总容量的20%,其中DG统一采用PQ 节点类型,功率因数为0.9[17-20]。其中,《分布式电源接入电网技术规定》中接入系统的原则要求:DG 允许并总容量原则上不超过上一级供电区域最大负荷的25%。IEEE-33节点标准系统图如图1所示。

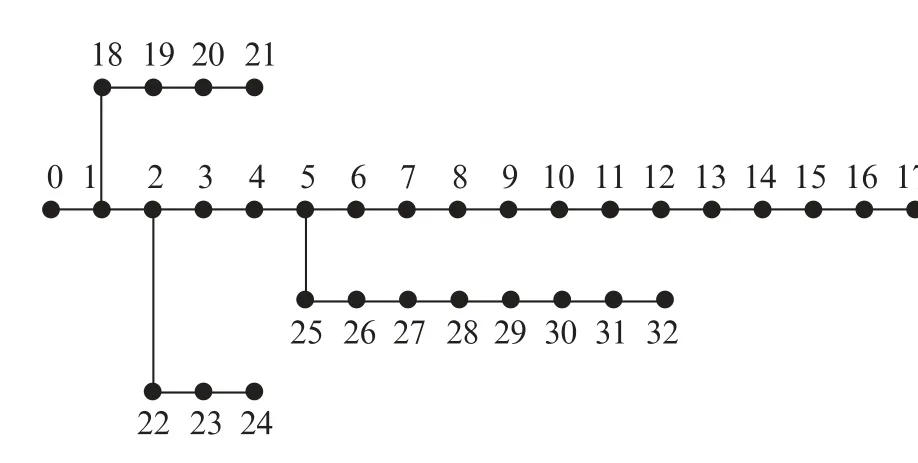
图1 IEEE-33节点配电系统

本文提出的IACS-IGA 算法应用于DG的配置结构优化,并结合IEEE-33系统进行验证。通过比较GA、CS算法和自适应遗传算法(Adaptive Genetic Algorithm,AGA)在相同条件下的收敛结果,验证了本文所提出的IACS-IGA 混合算法不仅能更好地逼近最优解集,而且迭代收敛的稳定性非常好,体现出该算法在分布式电源的未来并网方面比其他算法更具有规划安装容量和安装位置的优势。并且,改进算法对非线性多峰问题具有很好的处理能力。各算法优化迭代收敛过程对比如图2所示。

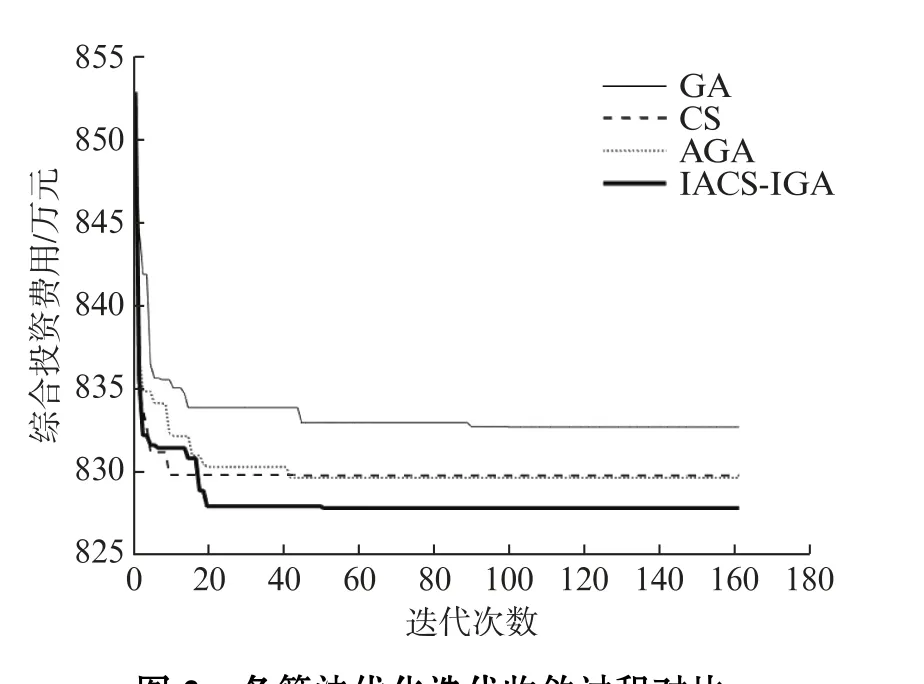
图2 各算法优化迭代收敛过程对比

运用IACS-IGA 在IEEE-33节点系统上进行DG的配置结构优化,配置结构优化结果表明:合理加入DG与不安装DG的配电系统相比,综合投资费用从979.2万元减少到827.8万元,减少量占未加入DG时的15.5%。节点电压标幺值的平均值从0.91上升到了0.93,电压的整体水平大大提高,根据潮流计算公式可知,传输功率一定时,随着电压水平的提高,线路的功率损耗会减少,从而增加了线路的传输效率,提高电能利用率。运行结果如图3所示。

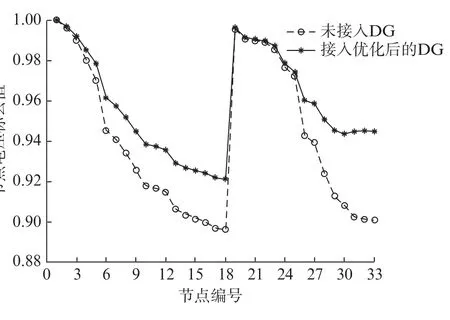
图3 各节点电压的变化曲线

采用IACS-IGA对算例进行DG 的配置结构优化,优化结果显示:合理加入DG 与不安装DG的配电系统相比总支路损耗费用从33.9万元下降到了17.5万元,减少量占总支路损耗的48.4%。详细的各支路有功功率损耗的变化曲线如图4所示。

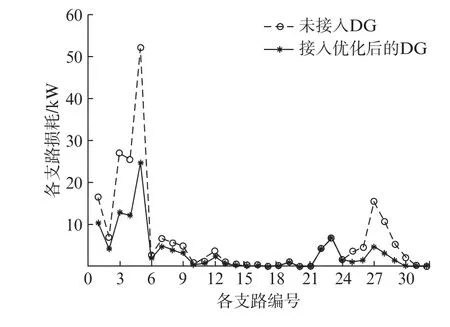
图4 各支路有功功率损耗的变化曲线

4 结 语

本文在IGA中引入IACS,形成IACS-IGA 混合算法。采用该算法对分布式电源配置结构优化模型进行求解,在IEEE-33节点系统中验证。通过比较分析多个算法,验证了本文所提出的IACSIGA混合算法在分布式电源配置结构优化中的优势。结果显示,该算法能够大大提高各节点的电压水平,减少有功功率的网络损耗。