永磁同步电动机模糊PI直接转矩控制

石志强, 李润伟, 周 枫

(1.北京京能清洁能源电力股份有限公司内蒙古分公司 生产管理部, 内蒙古 呼和浩特 010070;2.福氏新能源技术(上海) 有限公司 技术部, 上海 201315)

永磁同步电动机因其具有控制方便、机械特性好、效率高、成本低等优点,而被广泛用于风力发电机组。随着我国风电系统的推广应用,风电中的永磁同步电动机的控制问题也越来越受到关注[1-3]。随着控制理论研究的深入,永磁同步电动机的控制方式也多种多样[4-6]。直接转矩控制(Direct Torque Control,DTC)是近年来使用较广的控制策略。由于DTC出现较晚,仍然存在一些问题,例如转速超调,磁链、转矩波动较大等,在一定程度上受到了实际应用的限制[7-9]。

为了解决直接转矩中转矩及磁链脉动较大的问题,文献[10]对控制系统中滑模观测器在估计时存在的抖振问题,将具有扰动观测和补偿能力的滑模速度控制器取代了传统的PI控制器,能够有效改善控制系统的动态响应能力。文献[11]针对PI参数直接影响控制系统的动态响应的问题,提出采用混沌蚁群算法来优化参数,但实际效果不够明显。文献[12-13]在DTC中引入空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)技术,取代传统控制中的开关表,改善了开关频率问题,而且减少了开关损耗。但控制系统过于依赖电机的参数变化,系统的响应速度较慢。

基于以上问题,本文设计了磁链、转矩和转速模糊PI控制器,并且采用了SVPWM 控制,使得电机系统的抗干扰能力得到了大大提升。仿真和实验的结果表明,基于模糊PI控制策略的电机系统中的磁链、转矩脉动得到了有效抑制,突加负载后的系统响应速度也得到了提升。

1 永磁同步电动机的数学模型

为了研究的方便,本文采用通常情况下的永磁同步电动机的数学模型[14]。

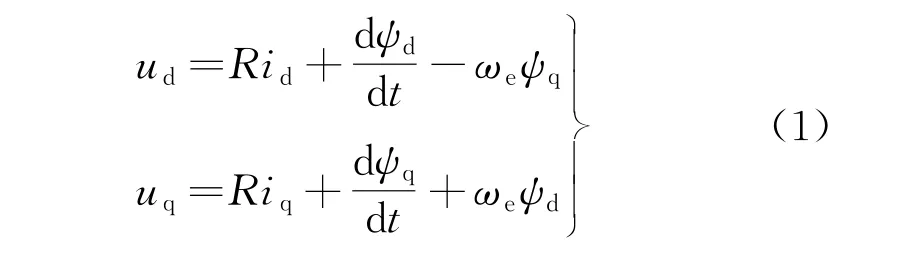
永磁同步电动机的d-q轴定子电压方程为式中:ud、uq分别为定子电压在d-q轴的分量;id、iq分别为定子电流在d-q轴的分量;ψd、ψq分别为d-q轴的磁链分量;R为定子电阻;ωe为电动机的电角度。

永磁同步电动机的定子磁链方程为

永磁同步电动机电磁转矩方程为

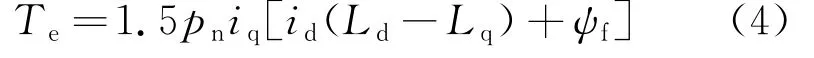
式中:pn为电机极对数。

对于表贴式的永磁同步电动机而言,其Ld=Lq,则电动机电磁转矩方程为

2 基于模糊PI控制器设计

模糊理论是根据专家知识和经验通过语言变量表达后,再根据模糊逻辑理论形成模糊规则,由此总结为控制算法。因此,该控制算法对于精确的数学模型没有要求。具体的控制模型结构如图1所示。e为控制器的输入误差,ec为误差e的一阶导数,ΔKp为比例系数的修正值,ΔKi为积分系数的修正值。控制器的具体流程为:控制系统首先实时检测e、ec,同时对其进行模糊化处理;其次针对所制定的模糊控制规则进行模糊处理;最后进行解模糊化,对输出的比例系数、积分系数进行在线修正。e、ec和ΔKp、ΔKi的模糊子集为{NB,NM,NS,ZO,PS,PM,PB},分别代表负大、负中、负小、零、正小、正中、正大。

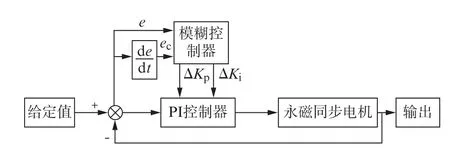
图1 模糊PI控制器结构

控制器整定后输出的比例系数Kp、积分系数Ki为

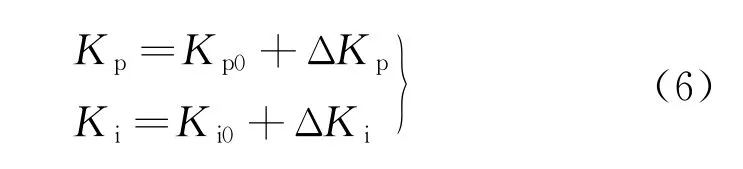
式中:Kp0、Ki0分别为Kp、Ki的初始值。

在模糊控制理论中最主要的是模糊规则的确定,根据实际中的经验所得来确定ΔKp和ΔKi的模糊控制规则,如表1和表2所示。

表1 ΔK p 的模糊控制规则

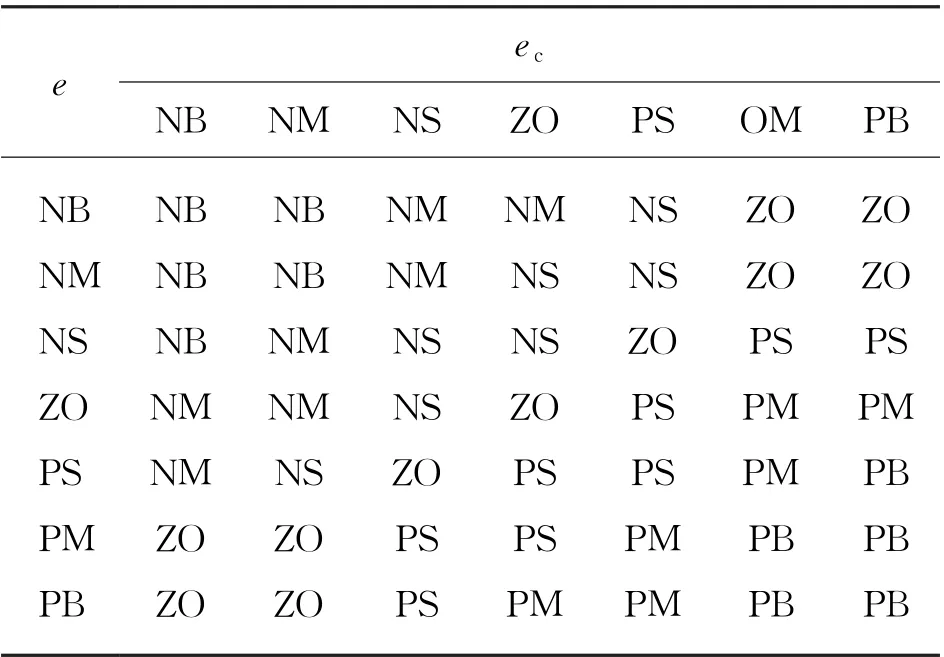
表2 ΔK i 的模糊控制规则

以永磁同步电动机DTC中转速环的模糊PI控制器为例,对转速环PI参数进行在线优化。当e变大时,为了将系统的响应速度提高,ΔKp应变大。为了使系统产生较小的超调量,应将积分系数限制饱和,因此应将ΔKi变小。当e和ec处于中等大小时,为了保证一定的响应速度的同时减小超调量,ΔKp应减小,ΔKi应大小适中。当e变小时,为了消除系统存在的静态误差,ΔKp和ΔKi应变大[15]。转矩环和磁链环的模糊PI控制结构跟转速环大致相同,这里不再赘述。根据实际实践经验,e、ec的论域为[-3,3],ΔKp、ΔKi分别为[-0.3,0.3]、[-0.06,0.06]。

3 系统仿真及实验结果

为证明本文所提出的控制策略的可行性,基于Matlab/Simulink搭建传统的DTC 和改进后的DTC进行仿真比较研究。改进后的控制框图如图2所示。

图2 基于模糊PI的DTC框图

图2中:ωr为电动机实际转速;ω*r为电动机额定转速;Te为电动机实际转矩;T*e为电动机参考转矩;|ψr|为电动机实际磁链;|ψ*r|为电动机参考磁链;Udc为电动机额定电压;uαβ、iαβ分别为静止两相坐标系下的电压、电流;uabc、iabc分别为静止三相坐标系下的电压、电流。

为了进一步对本文所提出的控制策略进行验证,搭建了基于Opal-RT公司开发的RT-LAB半实物仿真平台。选用的永磁同步电动机参数:R=12.9Ω,Ld=8.5 mH,Lq=8.5 mH,ψf=0.175 Wb,J=0.8 g·m2,pn=4。

对传统的PI-DTC控制与基于模糊PI改进后的模糊PI-DTC控制分别进行转速、转矩和磁链仿真。设置给定转速n=600 r/min,电动机系统在0.2 s后突加负载转矩1.5 N·m。

3.1 转速仿真及实验

由图3(a)可见,模糊PI控制系统的超调较小且能够很快跟上系统,达到给定转速时间为0.035 s左右,动态性能好,转速响应快。而PI控制系统出现较大的超调,并且达到给定转速时间为0.08 s,相对模糊PI控制系统时间增加了0.045 s。PI控制系统的动态性能远低于模糊PI控制系统。在0.2 s时突然加入负载转矩1.5 N·m,模糊PI控制系统转速有较小波动,波动范围在599.2～600 r/min之间,转速在0.200 5 s达到稳定。而PI控制系统,有小幅度的波动,波动范围在593.2～600 r/min之间,转速在0.26 s左右达到稳定。由此可以得出,相对于PI控制系统,模糊PI控制系统转速波动范围减少了6 r/min,恢复时间减少了59.95 ms。这说明模糊PI控制策略的动态性能好,能够有效提高系统的动态性能和抗干扰性,同时极大抑制了转速的超调。通过图3(b)、(c)可以看出,转速实验波形基本与仿真波形一致。

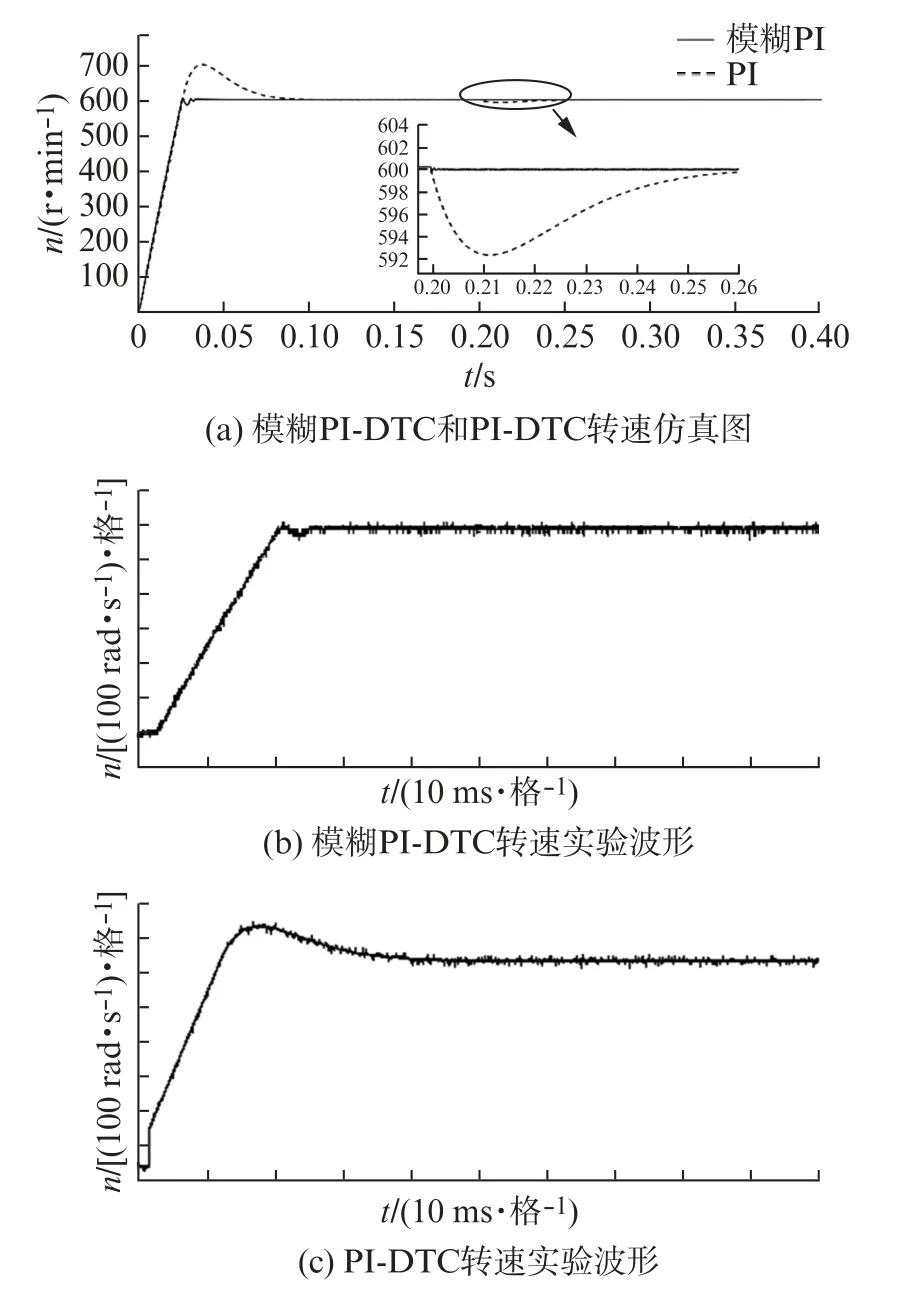
图3 模糊PI-DTC策略和PI-DTC策略转速波形图

3.2 转矩仿真及实验

由图4(a)可见,在启动时,由于模糊PI控制系统需要对PI控制器的2个参数进行在线寻优,会出现1个参数不稳定波动的过程,所以相较PI控制系统,模糊PI控制系统在启动时存在较大波动。但是,这个寻优过程能很快过去,在35 ms左右模糊PI控制系统趋于稳定,而PI控制系统在0.08 s左右才趋于稳定。在0.2 s时加入负载转矩扰动,模糊PI控制系统能够迅速稳定达到所给定的转矩值,波动范围大致在1.4～1.65 N·m。PI控制系统在0.2 s加入负载转矩时,达到稳定的时间较长,转矩的波动范围在1.35～1.65 N·m。由此可以看出,模糊PI策略和PI策略转矩波动大致相同,但是模糊PI策略能够迅速达到稳定,提高了系统的控制精度和系统稳定性。通过图4(b)、(c)2种控制策略的实验波形可以看出,转矩的响应和抗干扰性的变化与仿真结果相同。

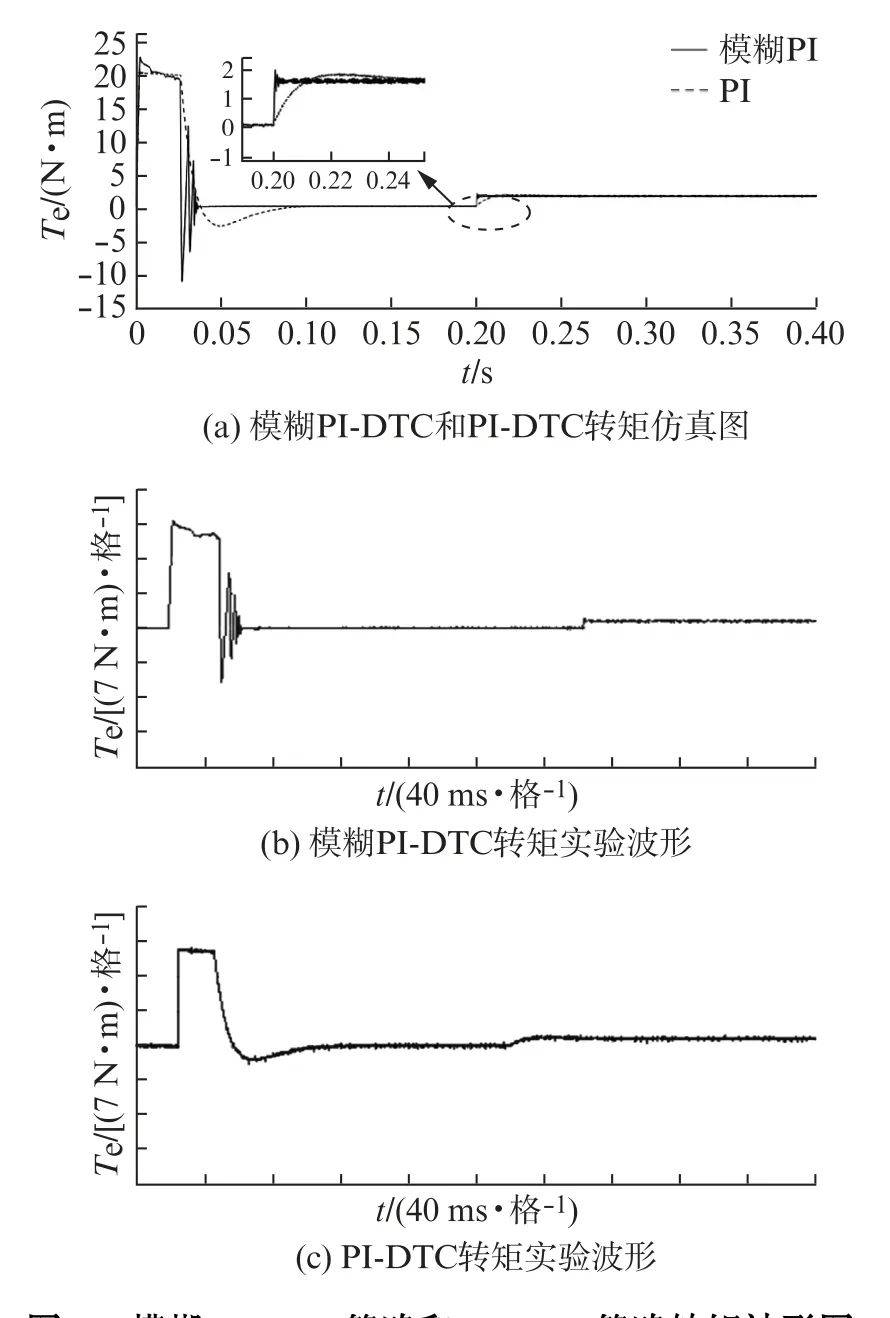
图4 模糊PI-DTC策略和PI-DTC策略转矩波形图

3.3 磁链仿真及实验

图5(a)为模糊PI策略和PI策略的磁链对比波形图。模糊PI策略磁链的波动范围为8 mWb。PI策略磁链波动范围为0.01 Wb。因此,本文提出的控制策略能够在一定程度上抑制磁链的波动,减小磁链的波动。从图5(b)、(c)2种策略的实验波形中可以看出,磁链响应的仿真波形和实验波形基本一致。

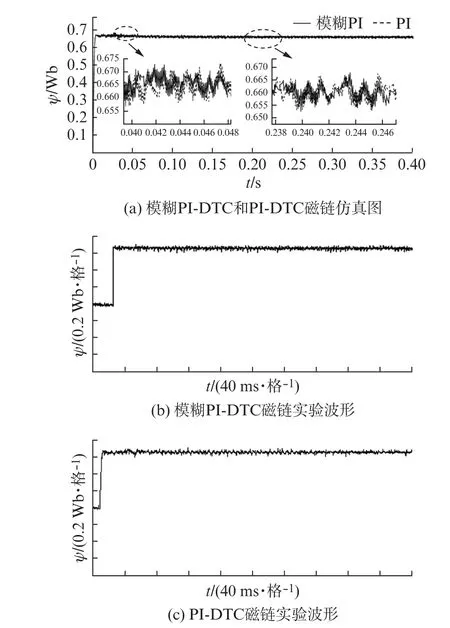
图5 模糊PI-DTC策略和PI-DTC策略磁链波形图

4 结 语

本文设计的模糊PI-DTC控制策略,可取代传统的PI-DTC控制策略。仿真和实验表明:将模糊PI-DTC控制策略融入电机控制系统,能够有效地抑制转速的超调,并且系统的抗干扰性和鲁棒性有所改善;采用模糊PI-DTC控制策略,系统在突加负载转矩后的0.01 s内转矩就达到了稳定;相比传统PI-DTC控制策略,模糊PI-DTC控制策略可使电机系统中的磁链脉动得到抑制。