ABAQUS二次开发在直齿轮弯曲应力分析中的应用

王玉玲，张荣闯，李明

（1.沈阳城市建设学院机械工程学院，辽宁 沈阳 110167；2.东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004）

齿轮作为机械产品传动部件应用中最为广泛的零件，对其进行弯曲应力分析是保证使用寿命和传动能力的前提。目前，齿轮弯曲应力计算的各类计算标准中，大多数基于Lewis公式，该公式基于材料力学等强度悬臂梁假设，没有考虑齿根截面的突变，同时忽略了轮齿径向载荷对应力的影响，导致不能准确地反映齿轮的弯曲应力［1-3］。有限元分析法的应用，能够准确地描述轮齿的几何形状、边界条件以及载荷状况，使齿轮弯曲应力计算更加便捷准确。然而采用CAE软件进行齿轮弯曲应力分析，图形界面操作过程繁冗复杂，仿真分析效率较低［4-7］。有限元分析软件ABAQUS采用基于特征的参数化建模方式，具有基于Python脚本编程的二次开发功能，其高效性和便捷性已得到验证［8-9］。本文采用Python语言编写内核脚本程序，从而控制ABAQUS内核操作，实现齿轮弯曲应力有限元分析的参数化和自动化。

2 轮齿几何建模

采用三齿模型进行齿轮弯曲应力分析。齿廓几何模型采用文献［10］的圆弧过渡曲线齿廓模型，如图1所示，坐标系OG-XGYG为齿廓坐标系，原点OG位于齿轮中心，坐标轴OGYG与齿廓中心线重合，rf、rb、r以及ra分别为齿根圆、基圆、分度圆和齿顶圆的半径，过渡曲线采用圆弧曲线，其分别与渐开线、齿根圆弧相切于B点和D点，圆心位于E点。

图1 齿廓几何模型Fig.1 Tooth profile geometry model

齿廓计算的各关键点坐标计算公式如下：

式中：ΩS为1/2基圆齿厚对应的圆心角，ΩS=π/2z+θn，θn=tanαn-αn，αn为分度圆压力角，z为齿数；SR为轮缘厚度，SR=htmB，mB为轮缘齿高比，SR的大小直接影响齿根弯曲应力，根据标准GB/T/ISO 6336-3∶2019，mB取值为1.2，此时可忽略轮缘厚度对齿根弯曲应力的影响。

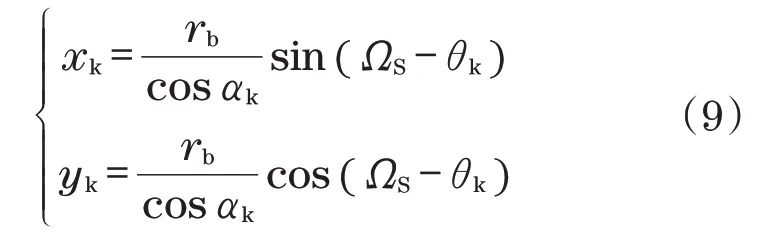
式中：αk、θk分别为K点对应的压力角和展角，θk=tanαk-αk，αk的取值为0≤αk≤arccos

3 有限元模型的建立

在低速重载齿轮传动中，需要按照弯曲强度计算齿轮的承载能力，即分析齿轮危险截面处的最大弯曲应力。假设齿轮传动为匀速传动，忽略轮齿误差。z1齿轮的精度等级为6级，计算齿根基本应力值σF0为44 MPa，应力修正系数YS为1.97；转速为200 r/min，转矩为120 kN·m。齿轮的相关几何参数见表1，z1齿轮的材料特性见表2。

表1 齿轮几何参数Tab.1 Gear geometric parameters

表2 z1齿轮材料特性Tab.2 z1 gear material

3.1 边界条件与载荷

常用直齿轮传动重合度系数一般在1～2之间，传动过程中会出现单齿、双齿交替啮合现象；当轮齿在单对齿啮合区外界点啮合时，只有一对轮齿承载，此时齿根所受的弯矩最大。因此，齿轮的齿根弯曲应力应该按载荷作用于单对齿啮合区外界点来计算。如图2所示，B1为单对齿啮合区外界点，通过式（10）可以求取坐标系OG-XGYG下的载荷作用点（x0，y0）。

图2 单对齿啮合区外界点计算Fig.2 Determination of highest point sign tooth contact

αFen载荷作用角用来确定集中力载荷Fn的方向：

假设齿轮运动传递扭矩为T，单对齿啮合区外界点集中力载荷Fn为

位移约束施加在左右轮缘和底部轮缘，约束全部位移。载荷施加与边界条件定义如图3所示。

图3 载荷施加与边界条件定义Fig.3 Load application and boundary condition definition

3.2 网格划分

网格划分是否合理，直接影响着有限元分析计算的精度和效率；为了保证齿轮网格划分的质量以及参数化实现，采用分块划分的策略；根据齿廓的几何形状、载荷作用点的位置，将单个轮齿切割为8个区域块，如图4所示。三齿模型的分块结果如图5所示。

图4 单齿模型区域划分Fig.4 Region division for single tooth

图5 三齿模型区域划分Fig.5 Region division for three teeth

单元形状四边形，单元类型为平面应变单元CPE4R，采用结构网格划分技术；网格划分时考虑齿的工作部分应力集中和计算效率，啮合齿廓和过渡曲线区域采用比较密集的网格，轮齿轮毂基体采用稀疏网格；网格疏密程度是通过控制区域块边界控制线的网格划分种子数量来实现的。

网格划分后的有限元模型如图6所示，整个模型共划分单元25 200个，节点25 731个。

图6 网格划分Fig.6 Mesh devision

4 仿真模型的代码实现

ABAQUS采用Python作为其脚本命令开发语言，在Python原有编程对象的基础上，融合了ABAQUS特有的Session、Mdb和Odb 3个对象。Session对象负责视图的控制与定义；Mdb对象负责齿轮的几何建模、材料定义、网格划分以及边界条件定义等功能；Odb对象负责仿真结果的输出。

4.1 几何建模

由图1可知，齿顶圆、过渡曲线、齿根圆和底部轮缘均为圆弧曲线，可以通过圆心点和两端点表示，例如表示为圆心E、起点B和终点D的圆弧曲线。轮缘FG为直线，可以通过起点F和终点G来表示。渐开线可根据式（9），表示为多个离散几何点拟合而成的样条曲线。对应于三齿齿廓可以通过对应几何曲线的坐标变换来求取。上述齿廓的几何模型形状取决于齿轮模数、齿数以及分度圆压力角，因此可实现参数化建模。几何建模的关键脚本代码如下：

s=mdb.models['Model-1'].Constrained Sketch(name='__profile__',sheetSize=200.0)

s.Line(point1=(),point2=())#两点直线构造侧轮缘;

s.ArcByCenterEnds(center=(),point1=(),point2=(),direction=CLOCKWISE)#中心点和两端点构造过渡曲线、齿根圆、齿顶圆和底部轮缘;

s.Spline()#样条曲线构造渐开线;

p=mdb.models['Model-1'].parts['Part-1']

f=p.faces

picked Faces=f.find At(coordinates=(0.0,r,0.0))

p.PartitionFaceBySketch(faces=pickedFaces,sketch=s)#轮齿区域划分主要在草图中通过直线分割面功能来实现。

4.2 材料定义

mdb.models['Model-1'].Material(name='Material-1')

mdb.models['Model-1'].materials['Material-1'].Elastic(table=((210000.0,0.3),))#定义弹性模量和泊松比;

mdb.models['Model-1'].Homogeneous Solid Section(name='Section-1',material='Material-1',thickness=None)#创建截面;

region=p.Set(faces=f,name='Set-1')

p.SectionAssignment(region=region,sectionName='Section-1',offset=0.0,offsetType=MIDDLE_SURFACE,offsetField='',thicknessAssignment=FROM_SECTION)#分配截面。

4.3 施加约束和载荷

mdb.models['Model-1'].DisplacementBC(name='BC-1',createStepName='Initial',region=region,u1=SET,u2=SET,ur3=UNSET,amplitude=UNSET,

distributionType=UNIFORM,fieldName='',localCsys=None)#边界条件定义,施加约束;

KLM=a.DatumCsysByThreePoints(name='Datum csys-20',coordSysType=CARTESIAN,origin=(),point1=(),point2=())#载荷为集中力,集中力作用于单对齿啮合区外界点,方向垂直于渐开线,需要定义局部坐标系确定集中力方向,三点定义局部坐标系;

datum=mdb.models['Model-1'].rootAssembly.datums[KLM.id]

v1=a.instances['Part-1-1'].vertices verts1=v1.find-At(((),))#载荷作用点;

region9=a.Set(vertices=verts1,name='Set-9')

mdb.models['Model-1'].ConcentratedForce(name='Load-1',createStepName='applyload',region=region9,cf1=-1800.0,distributionType=UNIFORM,field='',localCsys=datum)#集中力施加。

4.4 网格划分

datumP=p.Datum Point By Coordinate(coords=())

d1=p.datums

p.Partition Edge By Point(edge=e1.find At(coordinates=)),point=d1[datumP.id])#网格的疏密程度通过指定边的种子数来确定。方便于不同区域网格的划分,需要将边以通过点的方式进行分割处理;

pickedEdges=e.findAt(((),))

p.seedEdgeByNumber(edges=pickedEdges,number=10,constraint=FIXED)#设定边的种子数量;

pickedRegions=p.faces

p.setMeshControls(regions=pickedRegions,elemShape=QUAD,technique=STRUCTURED)

elemType1=mesh.ElemType(elemCode=CPE4R,elemLibrary=STANDARD,

secondOrderAccuracy=OFF,hourglassControl=DE-FAULT,

distortionControl=DEFAULT)

elemType2=mesh.ElemType(elemCode=CPE3,elemLibrary=STANDARD)#设定单元类型;

p=mdb.models['Model-1'].parts['Part-1']

f1=p.faces

pickedRegions1=(f1,)

p.setElementType(regions=pickedRegions1,elemTypes=(elemType1,elemType2))

p.generateMesh()#网格划分。

5 仿真结果分析与对比

仿真结果如图7所示，左侧过渡曲线弯曲应力最大值为47.000 0 MPa，右侧过渡曲线弯曲应力最大值为41.559 7 MPa，鉴于载荷作用点为单对齿啮合区外界点应力修正系数Ys的影响，齿轮计算弯曲应力为88.65 MPa，有限元仿真与计算值相差较大，其主要原因是国际标准计算结果明显过于保守，同时采用圆弧作为过渡曲线，其抗弯和抗拉能力要优于外摆线的过渡曲线。

6 结语

本文准确描述圆弧过渡曲线的直齿轮齿廓数学模型，重点描述齿轮弯曲应力有限元建模过程中载荷施加作用点位置的计算方法以及边界条件的施加方式。根据网格划分的疏密要求，研究了齿廓几何模型的区域划分方法和网格种子分布方式。给出了齿轮弯曲应力有限元仿真模型基于Python的ABAQUS二次开发编程代码，实现了应力分析过程的参数化和自动化。应用基于Python的ABAQUS二次开发直齿轮弯曲应力分析，为齿轮传动过程其他物理特性的高效便捷有限元计算（例如接触分析）提供了借鉴。