压力容器开孔补强计算方法介绍及补强计算若干注意事项

朱 辉*

（中国五环工程有限公司）

0 引言

在压力容器设计制造过程中，容器壳体开孔是必不可少的过程。部分开孔是为了满足工艺正常操作需要，部分则是为了压力容器的安装、调试、检修及维护等。然而，开孔会使容器壁的强度遭到削弱，还会因壳体结构连续性遭到破坏而造成开孔边缘处产生局部应力集中现象。此外，开孔接管有时还会受到其他外部载荷（如管道外载荷、附加力和力矩以及温度载荷等）的影响，综合考虑结构材料本身就存在的差异以及制造及检验过程中的缺陷等因素影响，很多失效情况发生在开孔边缘。因此，在压力容器设计过程中应着重考虑开孔补强的设计问题，从而保证设备安全运行。

1 壳体开孔边缘应力组成及补强准则

当压力容器壳体上开孔以后，通常开孔处边缘会形成以下三种应力：局部薄膜应力、弯曲应力和峰值应力[1]。

1.1 局部薄膜应力

压力容器壳体通常需要承受内压引起的均匀的薄膜应力，即为一次总体薄膜应力。然而当壳体开孔后，其开孔边缘的应力是极不均匀的。且经研究发现，在距离开孔边缘较远处，壳体所呈现的应力水平基本没有太大的波动，但是在开孔的边缘则集中分布着相对较大的应力，即为局部薄膜应力。

壳体开孔处局部薄膜应力的补强准则是保证开孔局部截面处的静力强度或避免失稳。

1.2 弯曲应力

在压力载荷作用下，开孔处接管与筒体两侧壳体产生的径向膨胀量通常是不相同的。为了确保两元件在连接处的变形互相协调，必定会形成使其相互平衡的边界内力（包括横向剪力和弯矩）。受到边界内力的影响，接管端部和壳体开孔边缘会产生局部的弯曲应力，该应力通常为二次应力。二次应力的限制和补强准则一般需从稳定性角度来进行考虑。

1.3 峰值应力

在接管与壳体连接处以及开孔边缘通常还会形成因应力集中而导致的分布范围虽小，但应力值却可能很高的应力。该应力沿壁厚呈非线性分布，应力峰值中超出一次应力加二次应力的增量部分称为峰值应力。

开孔边缘的破坏失效通常与疲劳操作相关，对于该处应力的控制和补强准则是从疲劳强度进行着手，一般只考虑疲劳分析设计。

2 常用的开孔补强计算方法介绍

目前国内外较为常用的开孔补强设计方法主要为等面积法、压力面积法、分析法及压力-面积应力法等。

2.1 等面积法

等面积补强法是目前较为常用的一种补强计算方法，早在1925 版ASME 压力容器规范中就已经被提出并使用。目前我国GB 150—2011《钢制压力容器》、JB 4732—1995《钢制压力容器——分析设计标准》（2005 年确认）、美国ASME Ⅷ-1、日本JIS 等标准规范均使用该计算方法。其理论基础是在双向拉伸的无限大平板上开小孔时，只考虑开孔壳体中的拉伸薄膜应力，且以补强壳体的一次总体平均应力作为设计准则，因此该补强方法仅涉及静力强度问题[2]。

容器壳体因开孔而被削除了部分承载面积，因此该部分面积应由壳体和接管在其各自有效补强范围内额外的截面积或附加的补强元件(包括焊缝 )截面积等予以补偿。这也就呈现出该方法补强设计时的基本原则是补强的面积至少等同于开孔处壳体被削弱的面积，用公式可以表达为：

式中：A1——开孔处筒体承受压力所需的截面积；

A1、A2——分别为在有效补强范围内，壳体、接管除承受压力所需截面积外而富余的截面积；

A3——接管内伸时，内伸部分截面积；

A4——焊缝金属截面积；

A5——补强圈截面积（可分为内外补强圈）。

等面积补强法的特点是开孔处接管与壳体连接处一般为角焊缝，而且具有应力突变、应力集中点易产生以及受力状态不好等，其有效补强范围与开孔直径和开孔处接管或筒体厚度有关。其局限性主要表现在以下3 个方面[3]：

（1）等面积法并未考虑接管开孔区域应力不均匀分布的现象，即粗略地认为在补强有效范围内所有的补强金属面积上的应力都是相同的，实际上应力在该范围内的分布很不均匀。

（2）等面积补强法并未考虑开孔边缘的峰值应力，因此该方法不适合有频繁压力波动的疲劳容器。

（3）等面积法忽视了开孔处应力集中与开孔率ρ等对其的影响。实际上当开孔率较大时，开孔边缘不仅会有很大的薄膜应力而且还会因变形不协调产生较高的弯曲应力，此时再使用该方法进行补强计算则较为冒进。

2.2 压力面积法

压力面积补强法是欧洲一直沿用的一种开孔补强计算方法，早在1979 版西德AD 压力容器规范中就已被提出并使用，目前德国AD 2000，欧盟EN 13445，英国 BS PD5500，法国 CODAP，美国ASMEⅧ-1 强制附录1-7 及我国的HG/T 20582—2011《钢制化工容器强度计算规范》等标准中用于计算大开孔补强的方法其原理也是基于压力面积法[4-5]。

压力面积法的基本原理是指压力在壳体开孔面积上所形成的载荷与壳体、接管、补强材料面积在有效补强范围内所承受的载荷相平衡。该计算方法的通式为：

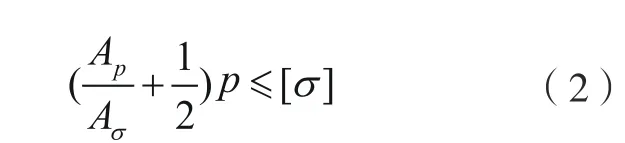
式中：Ap——为补强有效范围内的压力作用面积；

Aσ——为补强有效范围内的壳体、接管、补强金属的截面积；

p——为设计压力；

[σ] ——材料在设计温度下的许用应力

由式（2）可得：

式（3）左侧即为压力在受压面积上所形成的载荷，右侧则为材料所具有的承载能力。这就要求材料的承载能力应不小于压力所引起的载荷才能满足开孔处补强要求。

从初始计算方程形式上来看, 压力面积补强法与等面积补强法似乎完全不同，但对基本原理进行分析可以推导出,压力面积法所表达的承压截面积(有效补强范围内投影)和设计压力的乘积应不大于各元件承载截面积与其许用应力乘积的评定判据,而等面积补强法也同样可以表达为类似的原理，即由于开孔的缘故而造成承压截面积的削弱应由额外的同等截面积来进行补偿。因此，压力面积法和等面积法的基本原理是相同的。二者主要的区别在于对壳体以及接管有效补强范围的具体规定，压力面积法的补强范围跟开孔处壳体的直径和厚度有关，与实际的开孔大小并不相关，所以其开孔率可以达到1.0。

压力面积法仅考虑了开孔界面的一次总体强度，并未考虑开孔附近分布不均的应力，而且该方法也未考虑开孔边缘的峰值应力问题，因此对于压力频繁波动的疲劳容器，该方法也并不适用。

2.3 分析法

分析法是GB 150—2011《压力容器》标准中提供的一种开孔补强计算方法，该方法的理论基础是由清华大学薛明德、黄克智等所带领的研究组经过20多年研究后提出的。分析法是根据弹性薄壳理论并结合塑性极限和安定性分析而得到的[6]，它是通过一次加载和多次加载时有充分的塑性承载能力和安定性要求来保障开孔安全性，并通过在一定范围内限制开孔附近的等效薄膜应力和等效总应力来保证开孔处的稳定性。分析法适用于圆柱壳上大开孔接管的弹性薄壳理论解，该理论解也得到了后来人们大量的科学实验与精细网格的三维有限元解的进一步验证，更是得到国内外业界的强烈认可。

2.4 压力-面积应力法

压力-面积应力法指出在有效补强范围内，各承压元件上的应力并不是均匀分布的，应力在靠近接管处相对于其他各处较大，并且要求在开孔补强范围内的局部一次薄膜应力应满足所规定值[7]。而且在开孔有效补强范围的规定上，也同时考虑了因开孔所造成的应力集中和附加边缘应力的存在范围。该计算方法的计算通式为：

其中：σavg——平均一次薄膜应力；

σcirc——总体一次薄膜应力；

fN——容器外伸接管中由内压引起的力；

fS——壳体由内压所引起的力；

fY——由内压所引起的不连续力；

AT——所假设补强范围内的总面积；

Rxs——用于力计算壳体半径；

teff——用于计算靠近接管开孔处压力应力的有效厚度；

pL——在接管与壳体相交处的最大局部一次薄膜应力；

Sallow——接管与筒体连接处局部许用薄膜应力。

而上述计算公式所表达的内容跟压力面积法是一致的，这也是ASME 技术委员会介绍全新改版后的ASME Ⅷ-2—2007 版规范时提到该规范中所采用的开孔补强计算方法是以“压力-面积应力计算”为基础的，在2010 版ASME Ⅷ-1 标准中增加强制性附录1-10 开孔补强的另一种计算方法也是基于此方法，但是该附录在2017 版之后也已被删除。

3 补强计算若干注意事项

3.1 考虑纵向应力对开孔补强的影响

按规范要求进行开孔补强设计时，一般只考虑压力的作用，但对于高塔这类压力容器来说，除了压力载荷外，风载荷、地震载荷会使容器产生较大的轴向应力，当叠加以后的轴向应力超过筒体环向应力时，此时筒体的厚度应满足该轴向应力的要求。

因此对于采用等面积法进行开孔补强计算时就必须考虑由轴向应力所需的厚度来进行计算，而只考虑内压作用进行等面积补强设计是不充分且不安全的。然而国内外的标准和规范中并没有明确指出需要考虑这一点，而部分基于国外标准进行设计的计算软件如PV Elite 等则考虑了这部分载荷，进而保证了开孔补强设计的安全性。国内主要应用于辅助设计的计算软件SW6 则没有考虑此类情况，建议采用SW6 对细高塔进行开孔补强计算时，应校核轴向应力控制筒体厚度时的开孔补强是否满足要求。

3.2 保证开孔连接处结构的变形协调

在筒体开孔破坏了筒体结构的连续性，削弱了原有结构的承压能力，并且会使开孔边缘附近形成局部应力集中，美国橡树岭国家研究室试验研究的结果也证明了这一点。接管开孔处结构不连续，厚度差较大，两者的刚度差也就越大，在其变形协调过程中将会产生较大的边缘应力，耐冲击性能也相对较差。插入式接管与筒体的局部不连续也会形成局部不连续应力。

因此应尽量减小开孔壳体和接管等元件在结构、载荷和厚薄悬殊等方面的不连续程度，尽量使两元件能够刚柔相济，圆滑过渡，变形协调，避免直来直去，尤其是容易产生冷裂纹的材料。GB 150—2011 标准中提出，采用厚壁管进行开孔补强时，接管与相连壳体有效厚度之比宜控制在0.5～2。如不能满足补强需要，则应考虑局部增加壳体壁厚，采用接管内伸或嵌入式整锻件补强等方法进行处理。

3.3 注意结构不连续区域或大开孔等对开孔补强的影响。

压力容器通常因为结构设计的需要而使受压壳体连接处的结构不连续，如锥壳与圆柱壳筒体相接处，球冠形封头与圆柱壳筒体相接处，筒体或封头上的接管连接处等。因为总体结构的不连续，组合壳体在连接处周边的局部区域会呈现衰减较快的应力增大现象，通常称为“不连续效应”或 “边缘效应”。基于此而引起的局部应力也就被称为“不连续应力”或“边缘应力”。

压力容器的不连续应力具有局限性和自限性的特点，其应力水平也就有一定的衰减范围，因此应尽可能避免开孔落于不连续结构的衰减范围之内。

a） 圆筒体与椭圆形封头、球形封头、碟形封头的连接；

b） 圆筒体与带或不带折边的圆锥形封头或变径段的连接；

c）圆筒体与带或不带折边的平封头或平板的连接；

d）圆筒体与波形膨胀节的连接；

e）圆筒体与法兰的连接。

若因结构设计原因无法满足上述距离要求，建议采用有限元分析法对不连续结构处的开孔补强进行局部应力分析计算，以评估其危害性。

3.4 注意免除开孔补强计算接管的校核

GB 150.3—2011 第6.1.3 条及ASME Ⅷ-1 UG-36标准都规定了接管免除开孔补强计算的相关要求，相关的计算软件也会根据实际的结构参数进行判定并给出免除开孔补强计算的提示。但是该免除补强计算的规定也是基于理论和实际工程经验制定的，有时即使在所有开孔补强计算豁免的条件都满足的情况下，其实际的补强计算结果却仍不合格。而且在具体的工程实际中，也曾发生过压力容器壳体上的小接管因满足开孔补强计算豁免的要求未对其进行补强校核计算，最终该部位发生破坏的案例。因此，免除开孔不强计算要求应谨慎对待，出于安全考虑，在对成本不会造成太大影响的情况下，还是应对相应接管进行开孔补强计算，目前SW6 软件已经注意该方面问题并给予了结果提示， PV Elite 软件则需要主动对小接管开孔补强进行计算设置。对于不满足补强要求的接管应根据具体情况确定是否对其采取补强措施。

3.5 其他

对于大直径开孔补强的计算，还应考虑管道外载荷对于接管连接处应力叠加以及应力分布的影响。如采用局部结构的有限元应力分析方法进行计算，应注意除了应满足GB/T 150.1—2011 附录E 中的强度评定的要求外，还应注意该局部结构的制造、检验和验收要求应满足JB 4732—1995 的相应规定。

4 结语

本文介绍了目前国内外压力容器设计时开孔补强计算常用的计算方法，分析了各补强计算方法的原理及特点，有助于相关设计人员对于开孔补强计算方法的原理加强了解。

针对开孔补强计算，提出了平时在进行开孔补强计算时可能存在或易于忽视的问题，提请大家注意或采取相关措施进行改进，对于在今后设计中保证设计的完整性、合理性和安全性等有较好的指导作用。