提升高中生数学解题能力的有效对策探索

郝　雪

提升高中生数学解题能力的有效对策探索

郝雪

（福建省南平市高级中学，福建南平353000）

高中阶段数学知识本身具有较强的综合性，学生需要解决的题目多数具备较高的难度，需要学生积极应用自己的逻辑思维以及想象能力等对其中的要点进行提取，这样才能够在解题的时候具有更高的效率。数学问题的解答能够让学生的文字分析能力获得根本性的提升，无论是解决课堂中的题目还是生活中的问题都能够给予学生足够的锻炼机会，让学生数学综合实力获得进一步的强化，学生也能够有能力迎接难度更大的挑战。为了能够切实提升学生的解题能力，教师需要进行多方面的思考，根据班级学生的学情制定出最适合的授课计划，为学生后续发展奠定坚实的基础，提高学生的思维创造能力。本文对现阶段高中数学教师的授课方式进行了分析和总结，并提出一些切实可行的教学方式，旨在帮助更多教师运用多种教学手段完善以往的课程环境，让学生能够在进行知识解答的时候具有更广阔的思路，让数学知识能够在其脑海中形成完善的知识网络，这是每个教师都需要积极思索的问题。

高中课堂；数学教学；解题能力

解题能力的提升对于促进高中阶段学生快速成长具有十分重要的促进作用，让学生能够对数学知识有更加深入的理解。学生能够在解答数学问题的时候将所有的数学知识点灵活运用，对于数学知识要点的理解会更加深刻，其创新思维模式能够在这种完善的教学环境中得到充分挖掘。同时，数学知识的解答也能够给予学生完成查漏补缺的机会，学生能够切实了解到自身存在的不足之处，在每节课程中都能够着重研究和听取教师讲解的相关的解题技能内容，逐步完善自身的不足之处，帮助学生更好地完善自己在数学领域的缺陷。为了能够切实帮助学生高质量地完成各类数学题目，教师在制定教学计划的时候应该多角度思考，积极利用课余时间与班级学生进行深层次的交流，或者定期组织学生参与简单的课堂测验。这样能够更全面地了解到学生面临的学习问题，根据这些具体的数据信息制定出更适合的数学知识教学计划，让学生在进行解题的时候可以找到真正适合自己的方法，能够在题目中提取到真正有价值的条件信息，并灵活使用知识点对其进行合理解答。

一、高中生数学解题能力薄弱的主要原因

（一）学习方法不够科学

高中阶段的数学知识相较于小学或者是初中阶段的内容，不仅需要对其中的基础知识进行深入了解，还需要学生逐步建立适合的学习思维模式，并且需要掌握真正适合自己的学习方法。很多学生在研究的过程中仅仅是机械化地背诵其中包含的概念性知识，而对于其中的真正含义和推导过程并没有深入理解。这些知识在学生的脑海中是零散分布的，并不能够构建真正属于学生的数学知识研究大厦。学生在面对具有难度的题目时会存在思考不周的情况，思绪和思路都是极其混乱的。再者，很多学生在解决问题的时候并不能深层次地思考自己此前学习的公式、定理和题目的关联性，而是在解题的过程中认为可能会用到何种知识点的时候再查阅教材，但是学生并没有将其中的要点记忆在头脑中，即便能够将题目解答出来，也并不能够在后续的解题环节中将知识点进行使用。再加上很多学生忽视对知识体系的构建，导致在学习的过程中只是在做无用功。

（二）在解答题目的时候会过分依赖题海战术

很多学生为了能够在后续的学习过程中得到能力的提升，则会选择解决更多的题目。虽然题海战术在很多时候能够帮助学生形成一定的思维记忆，但是学生在这样的题目解答过程中也十分容易进入到思维定式中，在面对很多新的题目时则会无从下手，使学生获得事倍功半的学习效果。这种低下的学习效率会导致学生对于学习数学知识的自信心受到影响。学生在这样的环境中应该注重构建真正适合自己的解题体系，并且需要对各项知识点的核心要点进行精准记忆，这样才能够获得学习能力根本性提升。

（三）学生在面对很多新型学习方式的时候并不适应

在高中因为课堂教学时间有限，所以教师在传授知识的时候，为了能够节省更多的教学时间则没有对各种知识点都进行精确阐释，在布置课后作业的时候也不会针对每个学生的实际情况进行分层布置。这和初中以及小学阶段的教学方式存在着较大的差异性，学生在这样的教学氛围下无法对所有的知识点进行深入理解。再加上很多新型知识在学习和研究的时候需要学生针对性地展开多角度的思考，很多数学基础极其薄弱的学生更加无法跟随教师的步伐解决数学问题，对于很多知识点都是一知半解的状态。学生会逐步失去研究数学知识的自信心，在后续的学习环节中也无法真正融合到数学世界中，没有真正体会到数学知识具有的魅力，学生在进行题目解答的时候也会面对更多的困难。再加上高中阶段的数学题目难度较大，学生并不能够在较短的时间内解决其中存在的各种问题，其积极性会因此受到严重影响。为此，教师需要针对学生存在的上述问题展开多角度的思考，切实提高学生的数学解题能力。

二、提升高中生数学解题能力的主要途径

（一）强化学生的审题能力

审题能力在学生的整个学习过程中都占据着十分重要的地位，是决定学生解题答案准确性的关键因素。笔者通过调查和研究后发现，很多在解题过程中屡次出现失分情况的学生都是由于没有仔细审题，这就导致学生对于题目中的关键要点并不能够进行深刻了解，或题目条件提取不够全面，或对已知条件理解出现偏差，这都会造成学生对出题人的主要意图出现误解，导致任何的解题步骤都会存在疏漏或者错误的地方。为了能够切实减少出现类似情况的概率，教师需要做的就是培养学生的审题能力，让学生将题目的整体层次进行合理划分，将每个条件的要点进行理解，并分清其中的主次关系。其次，学生需要对题目中蕴含的隐藏条件进行精准分析。在高中数学题目中，很多条件并不能够在题目中直接体现，而是需要学生结合多种已知条件计算、分析获得。这些隐藏条件往往是解题的要点，学生只有经过多次审题后方可寻得。审题能力的提升换言之也是锻炼和挖掘学生分析隐藏要点的能力，让学生能够积极运用自己的智慧对其中的深刻内涵进行多角度分析。学生在研究各种题目的时候都会进行更细致地思考，这对于提升学生的综合实力是极其关键的要点。

比如，教师在讲授《一元二次方程》的时候就需要充分锻炼学生的审题能力。从题目上已知（3a-1）x2-5x+2=0有两个不相同的实数根，教师要求学生通过运算和分析找出a的取值范围。通过对此题目的仔细分析能够了解到，出题人已经明确告诉学生一元二次方程是关于a的，这也就意味着在方程式中“3a-1”这部分不能够为0，这个隐藏条件是需要学生经过分析后才能够得出的。教师在日常的教学中一定要提升学生在此方面的能力，让学生能够养成分析每个已知条件的习惯，能够逐步摸索出真正适合自己的数学解题方法，帮助学生更好地在后续的题目解答中利用这种思想解决各种难度更高的问题。

（二）提高学生的总结能力

教科书中为学生呈现的知识要点很多时候都是极其经典的，也是学生在研究数学知识的过程中需要深入思考的问题。其中的解题要点是经过数学领域专家深度讨论后的结果，具有较强的实用性价值，需要学生在日常学习过程中充分掌握，是学生解决各种困难题目的最基本技能。教师在教学环节中也需要组织学生对教材题目中涵盖的宝贵解题经验进行总结，让学生能够通过自己的理解对其中包含的知识要点精准掌握，并能够在后续的解题过程中更好地使用其中的知识要点。为此，教师需要组织学生在日常练习的过程中不断总结其中涵盖的解题要点。这样不仅能够让学生不断积累重要的学习经验，还能够让学生节省更多的学习时间，让学生能够将有限的学习时间进行高效利用。学生在长久的经验积累以及学习历程中能够锻炼其更高的解题效率和精准度，学生的数学知识研究自信心也能够在这样的环境中得到培养，其在独立解题的时候也具有自己的思路。

比如，教师在教学《集合》内容时就需要组织学生对其中的解题要点进行记忆。在《集合》的知识中学生会接触到融合“交集”和“并集”两种知识要点的题目，此类题目在很多情况下都具有较强的逻辑性，学生在自行解决相关题目的时候需要积极应用自己的文字分析能力和逻辑思维方式，只有这样才能够真正解决题目。但是，由于很多题目中的关键要点过多，如“参与美术兴趣小组的学生有32人，参与音乐兴趣小组的学生有34人，两种兴趣小组都参与的学生有12人，全班的总人数为56人。问参与美术兴趣小组但是没参与音乐兴趣小组的人数为多少”。这种题目当中的已知条件较多，教师可以引导学生利用Venn图解决相关题目，在草稿纸上分别画出代表参加美术兴趣小组和音乐兴趣小组人数的圆圈，并根据题目给出的条件调整圆圈的位置。这样能够以更加直观的方式展现出各种数据信息之间的关系，学生在进行题目分析的时候也不会出现遗漏关键条件的情况。学生在后续的相关题目解答环节也能够积极使用这种方便快捷的计算方式解决以往存在的问题，让学生能够在实践学习环节中不断总结自己的学习经验，让学生的解题能力能够逐步提升，提高学生的学习能力。

（三）教学环节阐释思维要点

在数学知识的研究过程中，教师需要尽可能地锻炼学生辩证思维的能力，让学生在面对任何题目的时候都能够找出多种适合的解决方法，并且能够在若干的解题方式中寻找出最适合的思路。这样既能够锻炼学生的多元化思维能力，也能够让学生在无形之中掌握更多角度的解题思路，学生的思维方式能够更加开阔。这对于帮助学生在数学领域迅速成长是极其重要的教学模式，是每个教师都需要重点研究和贯彻的教学思路，将自己的教学眼光放得更长远，让学生能够在更完善的环境中认真研究数学题目。学生的解题意识也因此能够从多个角度建立起来。当学生在学习的过程中已经对最基本的解题方法充分掌握并能够灵活使用后，教师则需要引导学生将其进行变通，在日常教学环节中就需要让学生注重使用辩证思维的思路解决数学问题，让学生能够对数学知识具有更加深入的理解，学生的发散性思维能力就能够在这样的环境中获得显著提升。

比如，教师在组织学生研究“判断函数奇偶性”的相关题目时就，可以积极利用这种教学思维。在进行题目解答的时候教师需要将学生放置在课堂的主要地位，提出一些引导性的问题让学生进行思考和判断，让学生能够在自行探索的过程中体会到题目解题的主要方式。当教师提出让学生判断函数f（x）奇偶性的时候，有的学生能够充分意识到使用函数图形的重要性。教师可以让学生将几个自然数代入到函数中，并在自己建立的坐标系中绘制出函数的图像，这样能够将文字化的信息转化为图像信息。教师对于学生的这种创新及问题思路需要给予足够的认同和赞许。在后续的解题环节中，教师需要让学生针对函数奇偶性的问题展开更多的思考，让学生说明自己的想法。有的学生在绘制出图像后发现其是关于原点对称，则得出其是奇函数的结论。这样的教学方式可以将更多的解题时间留给学生，让学生能够真正使用自己的智慧对其中的知识要点进行深入探究。这对于学生现阶段的解题思路能够起到良好的扩充作用，也能够让学生更好地将学习到的基础知识应用起来，切实达到学以致用的效果，让学生能够在后续的成长过程中更好地完善自己的思维方式。学生在研究数学题目的时候也会展开多角度的思考。

（四）培育学生的一题多解能力

在新课改的教学背景下，教师在执行教学任务的时候不仅需要注重将其中的基础知识要点进行细致阐释，更重要的是需要引导学生形成多种思考方式，教师在引导学生解决数学问题的时候也需要鼓励学生对其进行一题多解。这样能够让学生在思索的过程中进行多角度的思考，让学生能够在探究的过程中掌握多种解题方法，在潜移默化中寻找到真正适合自己的解题思路，有效提高学生的解题能力。

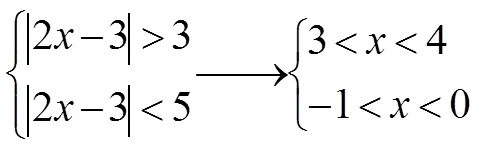
三、结语

综上所述，高中阶段的数学题目当中包含了诸多的综合型内容，学生在进行研究和学习的时候需要多角度的思索，不仅要对题目进行准确阅读，也要在字里行间找出隐形的有用条件，对数学题目的理解能够更加全面。教师还要培养学生在面对灵活多变的数学题目时拥有自己的思路，使学生能够从容面对各种题目，并在解决任何题目的时候都能够得心应手，促使学生的数学学习自信心能够得到显著提升。

[1] 郭荣炽.提高高中生数学解题能力的教学方法研究[J].读写算,2021(28):41-42.

[2] 陈鸿英.探析培养高中生数学解题能力的路径[J].名师在线,2021(17):39-40.

[3] 马力.高中生数学解题能力培养的教学策略[J].新智慧,2020(23):112+114.

[4] 姚园月.提高高中生数学解题能力的教学方法研究[J].数学学习与研究,2020(14):22-23.

G632

A

1002-7661(2022)28-0129-03