基于单天线载波相位差分的列车姿态解算方法研究
姜 维,李佳蕾,王 剑,蔡伯根
(1.北京交通大学 电子信息工程学院, 北京 100044;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;3.北京市电磁兼容与卫星导航工程技术研究中心, 北京 100044)
目前全球卫星导航系统(Global Navigation Satellite System, GNSS)在列车运行控制中的应用逐渐增多,通过卫星定位技术实现列车自主定位已经成为下一代列控系统发展的主要趋势[1-2]。在列车自主定位的过程中,轨道占用情况的准确识别是需要解决的首要问题。较为常见的基于车载设备完成轨道占用识别的方法主要通过GNSS提供位置测量,配合地图匹配等技术,并引入惯性导航系统等其他传感器进一步增强列车轨道占用设别性能[3-5]。根据铁路线路的一维性,利用GNSS进行轨道占用识别的情况主要包括平行线路和道岔区段。其中道岔区段由于有直向和侧向两个方向,且在岔尖附近,两个方向的股道距离很小,受到GNSS定位精度的限制,在这一区段的轨道占用识别难度更高。尤其在车场咽喉区,该区段是列车到发、调车作业等必经之地。由于咽喉区道岔汇聚,多股道并存且各股道之间间隔较小,更难保证轨道占用识别的准确率[6],因此需要引入其他方式来进一步提高准确率。目前常见的道岔辙叉角度为3°~6°,当列车进入此区段时,其航向角会发生较为明显的变化。因此可以引入GNSS姿态测量信息来辅助判断列车轨道占用状态,从而提高轨道占用识别的准确性[7]。Mueller研究的基于卫星导航的航向定位系统就是通过测量列车航向角,与车载地图的航向角对比来计算出列车进入正线或侧线的概率[8]。Heirich[9]提出利用粒子滤波、多传感器融合的列车定位算法中,也将列车姿态作为列车状态估计量之一,并且主要应用在交叉轨道区段的列车定位研究中。Lüddecke[10]认为地图匹配算法中,列车的航向角可以提供比位置坐标更精确的列车状态信息,可用于区分判断道岔区段两种前进方向,且列车移动的速度越快,测得的航向角就越准确。由此可见,在卫星信号状况良好的情况下,将列车姿态信息作为列车状态之一,并辅助其他传感器及轨道电子地图等设备进行列车轨道占用检查,可以在低成本的情况下进一步提高轨道占用检查准确度。
传统的高精度姿态测量信息主要是通过惯性导航系统递推得到,惯性导航系统具有自主、安全的优点,但它的动态漂移特性会导致它们的测量精度随着时间积累而降低[11]。GNSS测姿与惯导系统相比,具有终端设备简单、安装方便的优点,且不会有误差累积问题。目前大多数GNSS测姿方案采用两根及以上的天线,通过载波相位差分技术计算天线之间的基线矢量,然后根据载体坐标系与当地地理坐标系之间的转换关系计算姿态。这种方法求解得到的姿态精度较高,但也不可避免的存在天线安装要求高、天线支架庞大等问题,并且随着使用时间增加,天线支架还可能出现轻微形变,导致基线长度发生变化,从而姿态角的解算精度无法保证[12]。因此衍生出单天线测姿算法的研究,在20世纪90年代末,Kornfeld 等[13]便提出采用单天线伪姿态初步飞行试验,证明了单天线解算得到伪姿态的可用性。张鹏等[14]利用单天线解算得到的三维速度测量值求取载体的伪姿态,其结果与航迹发生器计算得到的理想姿态对比,误差可以保持在1°以内。孙芮等通过最小二乘法解算得到相邻历元间的位移矢量,并进一步计算偏航角,其中根据载波相位计算得到的姿态精度可达到1°左右,但在该算法中并未描述捕获卫星数量频繁变化时对姿态解算结果的影响[15]。上述文献中单天线测姿算法均被应用于汽车导航,但关于列车运行过程中的姿态解算研究很少。
为了在低成本的前提下引入精度较高的列车姿态信息辅助轨道占用识别,提高识别准确度,保证列车安全运行,提出一种应用于列车的单天线姿态测量方法。该方法利用共模误差在短时间内不变的特点,通过星间差分和时间差分相结合的双差模型,巧妙地消除了大部分误差,避免了复杂的误差建模过程,简化了算法的复杂程度。其中星间差分主要通过在一个历元中参考卫星与其他卫星的观测量之间差分,消除接收机钟差,形成单差载波相位。时间差分为相邻历元间观测量的差分,消除对流层误差、电离层误差、卫星钟差以及整周模糊度。将双差后的载波相位观测方程进行线性化处理,利用卡尔曼滤波估计前后历元间位移矢量的坐标以及速度的变化量。根据坐标系之间的转换关系进一步解算列车的航向角和俯仰角,实现基于单天线的列车姿态解算。
1 单天线测姿观测模型
1.1 GNSS观测量
GNSS主要通过向地面播发卫星信号实现定位授时功能,它的观测量包括伪距定位和载波相位两种。伪距定位根据卫星发送信号和接收机接收信号的时间延迟来计算传播距离,从而进行定位,其观测方程为
ρ=(tr-ts)·c
( 1 )
式中:ρ为伪距观测量;tr为接收机接收到卫星信号时的GPS时;ts为卫星信号发射时的GPS时;c为光速。
将卫星信号在观测过程中可能产生的误差分为三类:包括卫星的误差,如卫星钟差、星历误差等;传播过程中的误差,如对流层误差、电离层误差以及多路径误差等;接收机的固有误差,如接收机钟差等。将这些误差考虑之后,伪距观测方程可进一步写为
ρ=r+c(δt-dt)+I+T+ε
( 2 )
式中:ε为剩余残差;δt为接收机的时钟误差;dt为卫星的时钟误差;I为卫星信号传播路径中的电离层延迟等效距离误差;T为卫星信号传播路径中的对流层延迟等效距离误差;r为卫星与接收机之间的几何距离,可以进一步表示为
( 3 )
其中,(Xs,Ys,Zs)为卫星的位置坐标;(xr,yr,zr)为接收机的位置坐标。
载波相位定位是根据传输过程中载波信号的相位变化来计算传播距离,这样计算得到的距离是以周为单位。但是由于首次观测到的载波相位值中包含整数值无法测量,因此载波相位的测量值并不能直接用来测距,即实际的载波相位观测值必须包含一个整周模糊度未知数N,准确的整周模糊度需要通过模糊度固定算法求得,这也使得载波相位定位相比于伪距定位更加复杂。
载波相位观测方程为
λφ=r-I+T+c(δt-dt)+λN+ε
( 4 )
式中:λ为载波信号的波长;φ为载波相位测量值;N为整周模糊度。
载波相位定位相比于伪距定位引入新的未知数,即整周模糊度N,但由于载波信号的波长更小,因此载波相位的测量值精度更高,可达到厘米级的定位精度,更适用于高精度的定位场景。在姿态解算过程中,对定位精度要求较高,采用载波相位定位技术,并通过差分模型进一步降低定位过程中的各项误差。
1.2 单天线双差载波相位观测模型
由载波相位观测方程可以看出,载波相位的测量值受卫星钟差、接收机钟差,以及传播过程中电离层延迟误差和对流层延迟误差等误差源影响。其中,接收机钟差可以通过参考卫星与其他卫星之间差分来消除。首先选择一颗高度角最高的卫星作为参考卫星(假设参考卫星为第j颗卫星),则星间差分载波相位观测方程可以表示为
λφij=rij-Iij+Tij-c×dt+λNij+εij
( 5 )
式中:上标ij为第i颗卫星与第j颗卫星之间进行星间差分后的结果。
为进一步消除其他误差,在星间差分的基础上进行时间载波相位差分,即通过时间域的差分,用一根天线实现载波相位双差。当以很小的采样间隔对同一颗卫星持续观测时,由于相邻历元时间间隔短,因此整周模糊度、卫星钟差、对流层误差以及电离层误差认为不变,可以通过时间差分完全消除。图1为单天线载波相位双差示意。

图1 单天线载波相位双差示意
双差后的载波相位观测方程可以表示为
( 6 )
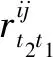
( 7 )
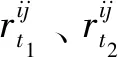
( 8 )
( 9 )
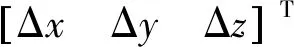
(10)
令
(11)
(12)
则式( 6 )双差载波相位观测方程可以进一步写成
(13)
2 卡尔曼滤波解算列车位移矢量
为了更准确地计算相邻历元间列车的位移矢量,选择卡尔曼滤波算法进行估计,卡尔曼滤波系统的模型包括运动模型和量测模型,运动模型是用来描述载体的运动状态,可以表示为
Xk=FXk-1+Wk
(14)
式中:Xk为系统的状态矢量(k时刻);F为状态转移矩阵;Wk~N(0,Q)为系统的过程噪声。
由于在列车运行过程中,位移矢量的速度变化量有较强的相关性,因此将系统的运动状态建模为一阶高斯-马尔可夫速度模型,预估状态Xk可以被表示为
(15)

系统状态转移矩阵为
(16)
式中:dT为采样间隔;I为单位矩阵。
系统的噪声矩阵为
(17)
式中:τ为相关时间;由于该模型中速度服从一阶高斯-马尔可夫分布,因此噪声误差主要体现在速度对应的维度中。
卡尔曼滤波中的量测模型为
Zk=HkXk+Vk
(18)
式中:Zk为系统观测向量;Hk为量测矩阵;Vk~N(0,R)为系统的量测噪声。
根据双差载波相位观测方程可以得到系统的观测矢量为
(19)
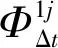
系统的量测矩阵H为
(20)
由于星间差分载波相位的量测值之间是具有相关性,而相邻历元间再进行时间差分后,量测值之间的相关性进一步增强,因此系统量测噪声的协方差矩阵R为
(21)
式中:σ2为载波相位观测量的噪声。
式(14)~式(21)为卡尔曼滤波过程中一些主要的参数矩阵设置。卡尔曼滤波是通过多个循环周期来不断提高估计的精度。在一个卡尔曼滤波周期内,包括时间更新和量测更新两个过程。时间更新是利用上一个历元估计的状态量来预测当前时刻的状态量,并计算其误差协方差矩阵来衡量预测的是否准确。量测更新是利用观测量对估计量进行修正的过程。其中预测的结果和量测结果所占权重大小是通过增益矩阵来调节的,从而使得估计值更接近于真实值。
此外,在卡尔曼滤波循环计算不同历元间位移矢量坐标的过程中,当捕获到的卫星数量发生变化时,还需要做进一步处理才能保证算法的普适性。当卫星失锁时,找到当前历元下跟踪失败的卫星,并获取卫星在序列中的位置,将上一历元中对应位置处的载波相位观测量去掉。当捕获到新的卫星时,先将当前历元的载波相位观测量传递给下一历元(为下一历元时间差分做准备)然后去掉当前历元中新增卫星的观测量,再与上一历元进行时间差分。
3 列车姿态角解算
3.1 坐标系定义及其转换关系
坐标系是卫星导航定位与测姿的基础,传统的姿态角定义为载体坐标系相对于当地地理坐标系的相对角位置。在单天线姿态测量中,还涉及稳定坐标系,以下是对三个主要涉及的坐标介绍。
(1)载体坐标系
载体坐标系(B系)也称为“右前上”坐标系,将天线相位中心定义为原点,沿着载体的纵轴向前的方向为y轴,沿着载体向右,垂直于载体纵轴的方向为x轴,垂直于xOy平面,沿载体竖轴向上的方向为z轴。
(2)当地地理坐标系
当地地理坐标系(N系)也称“东北天”坐标系,它的原点与载体坐标系原点定义相同,z轴在地心矢量方向上,y轴沿子午线向北,x轴由右手定则确定。
(3)稳定坐标系
稳定坐标系(S系)的y轴是沿着载体在当地地理坐标系中的速度方向,x轴垂直于y轴并且指向载体的纵轴方向,z轴与x轴和y轴垂直。
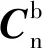
(22)
其中,
(23)
(24)
(25)
在列车姿态解算应用,主要讨论偏航角和俯仰角,其转换见图2。
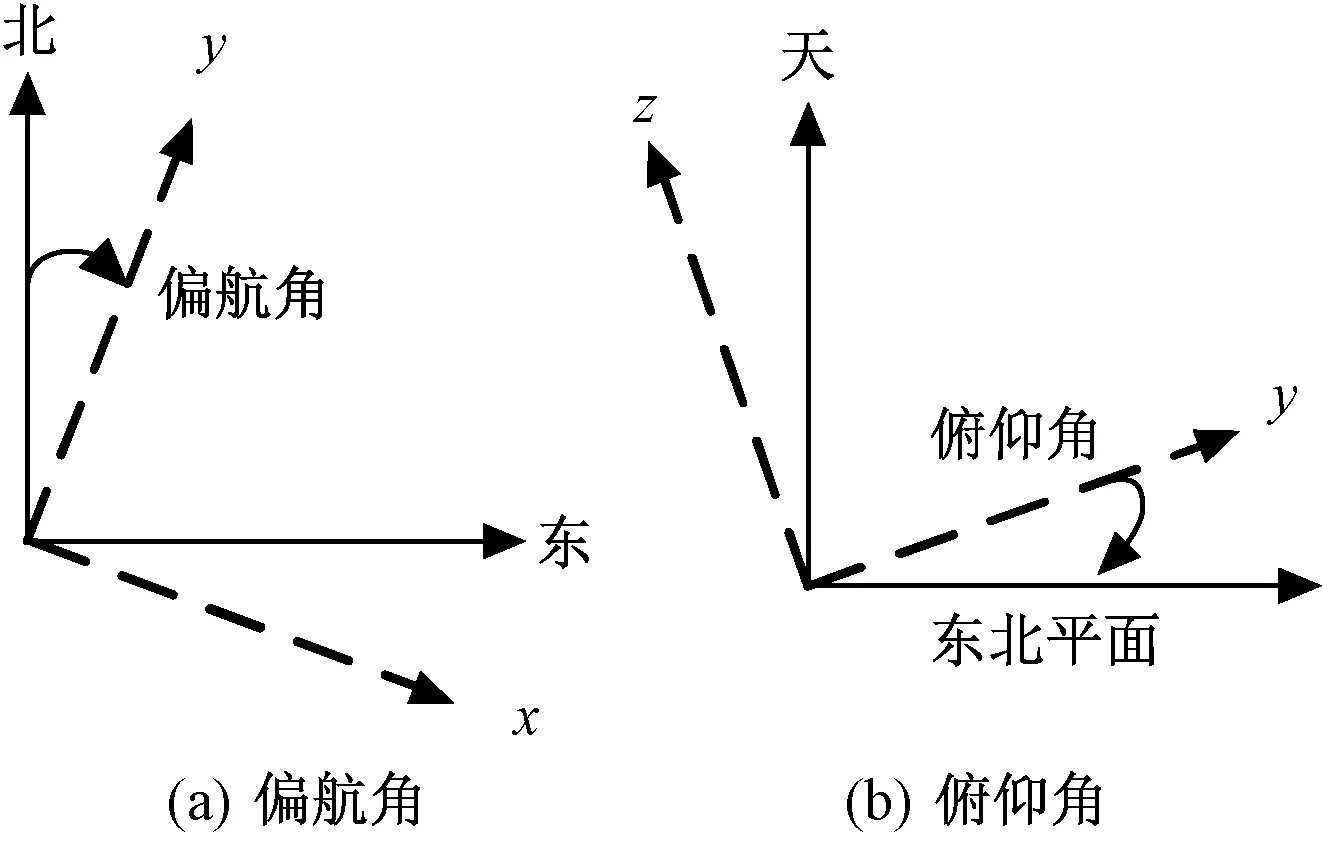
图2 坐标系转换关系
3.2 单天线姿态角求解方法
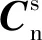
(26)
(27)
进一步推导得
(28)
(29)
4 实验仿真及结果分析
为了验证所提算法的可行性和普适性,选取了两组实验数据进行验证:分别是2019年6月和2021年7月在青藏线上采集的数据。在数据采集过程中,天线位于首节车厢顶部靠中间的位置,连接着SPAN接收机。将SPAN接收机输出的高精度信息解算得到的姿态角作为算法验证过程中的参考姿态角。
4.1 实验一
实验一采集数据约为15 min,数据的采样频率为10 Hz。图3为实验过程中列车行驶的轨迹。列车在运行过程中速度保持在18~22 m/s,速度变化见图4。

图3 列车运行轨迹示意(实验一)

图4 列车速度变化曲线(实验一)
在列车运行过程中接收机捕获到卫星数量变化以及对应的精度因子(Dilution of Precision,DoP)变化见图5。其中包括位置精度因子(Position Dilution of Precision, PDoP)、水平精度因子(Horizontal Dilution of Precision, HDoP)和垂直精度因子(Vertical Dilution of Precision, VDoP)。在整个实验一中,卫星信号质量较为良好,在3 000历元以前捕获卫星数量较为稳定,3 000历元之后,捕获卫星数量变化频繁,DoP值也有所波动,但整体捕获卫星数量大于或等于6颗。

图5 DOP值及捕获卫星数量(实验一)
图6为参考偏航角和解算得到的偏航角对比图。可以看出在2 500~3 000历元、4 000~4 500历元以及6 000历元左右列车的航向都发生较为明显的变化。将局部结果(1 100历元到1 300历元之间)放大后可以看出单天线测姿算法解算得到偏航角结果抖动更剧烈,但二者的误差保持在较小的范围内。
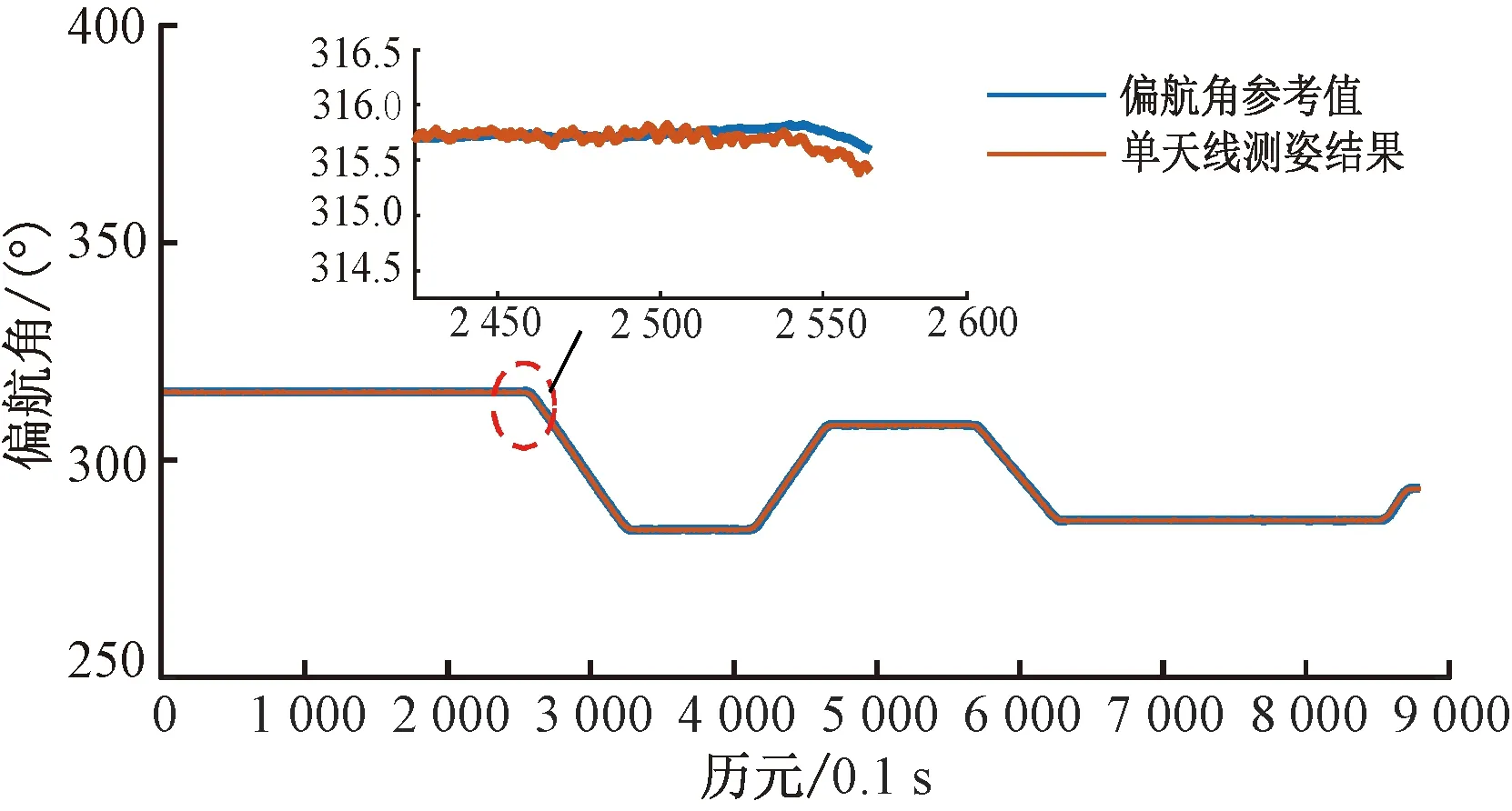
图6 参考偏航角与计算值对比(实验一)
图7为偏航角参考值与计算值之间的误差图,在3 000历元到6 000历元之间,由于捕获卫星数量变化频繁,因此偏航角结果有轻微波动。在8 000历元之后,捕获卫星数量下降至6颗,卫星DoP值增大,解算得到的偏航角精度也有所降低。但是整个过程中误差基本保持在±0.5°以内。
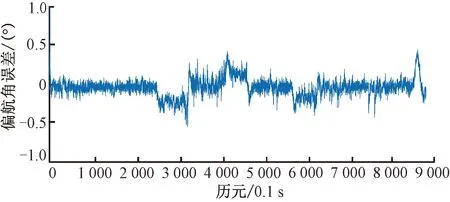
图7 偏航角误差(实验一)
图8为俯仰角参考值与计算值的对比图。由于列车运行过程中,大部分场景下俯仰角变化范围很小,因此解算结果的误差也保持在很小的范围内,见图9。

图8 俯仰角结果对比(实验一)

图9 俯仰角误差(实验一)
4.2 实验二
实验二选取数据共2 200历元,列车运行轨迹见图10,与实验二相比,列车运行的速度更慢,基本保持在11~15 m/s,见图11。
从图12卫星DoP值和捕获卫星数量变化情况来看,捕获卫星数量变化少,与实验一数据相比,整体卫星信号质量更良好。
实验二解算得到的偏航角误差见图13,整体误差保持在1°以内,其中在800~1 200历元,误差值增大,对应图14可以看出该区间内列车转向,偏航角变化20°左右。

图10 列车运行轨迹示意(实验二)
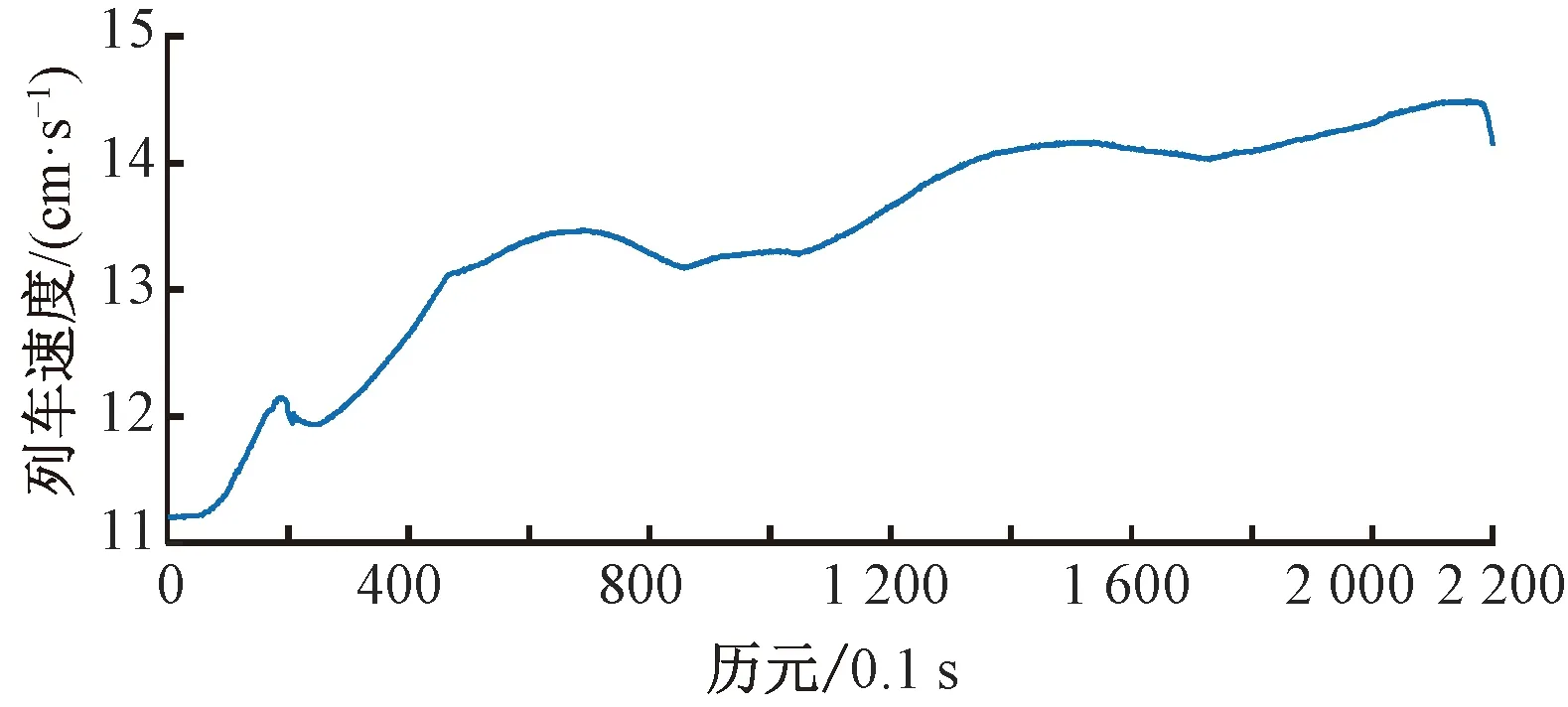
图11 列车速度变化曲线(实验二)

图12 卫星DOP值和捕获卫星数量(实验二)
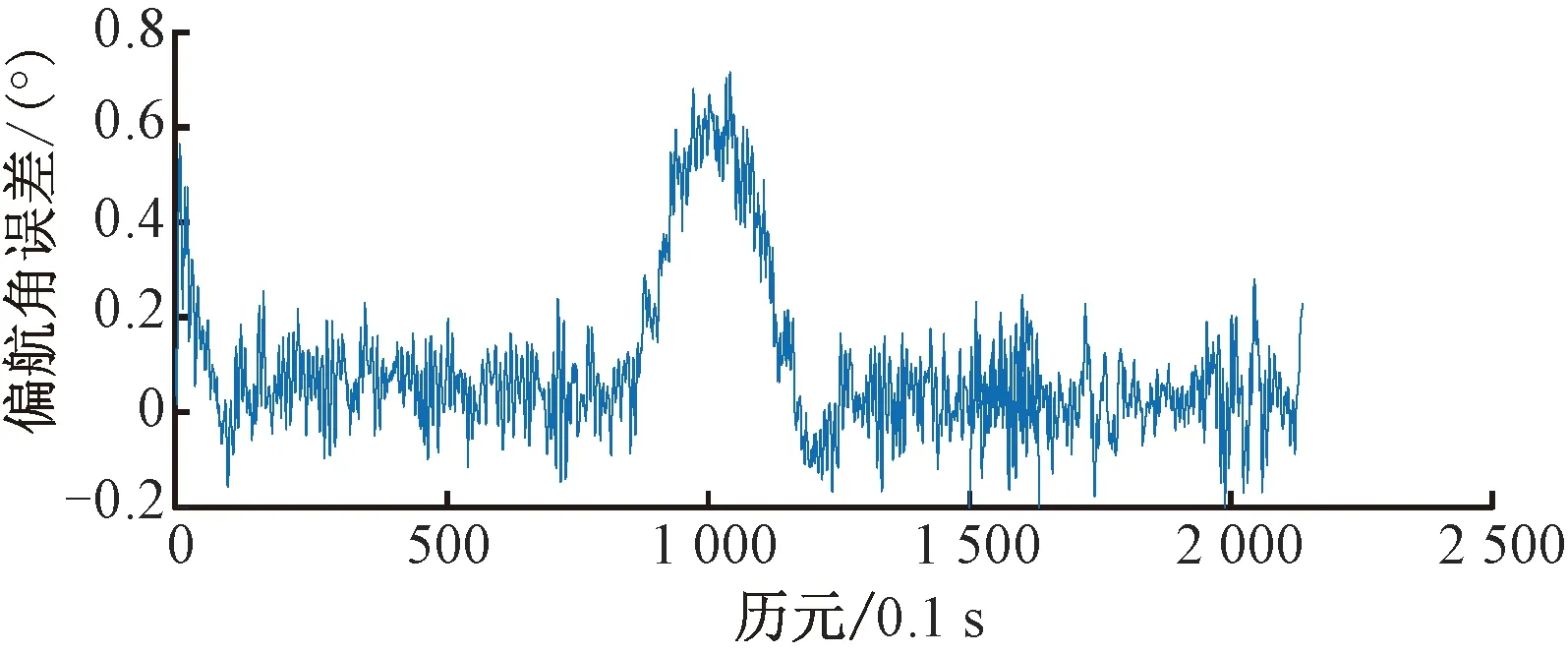
图13 偏航角误差(实验二)

图14 偏航角结果对比(实验二)
俯仰角解算结果与参考值对比见图15,与实验一结果类似,由于变化范围很小,所以误差也保持在较小的范围内,见图16。
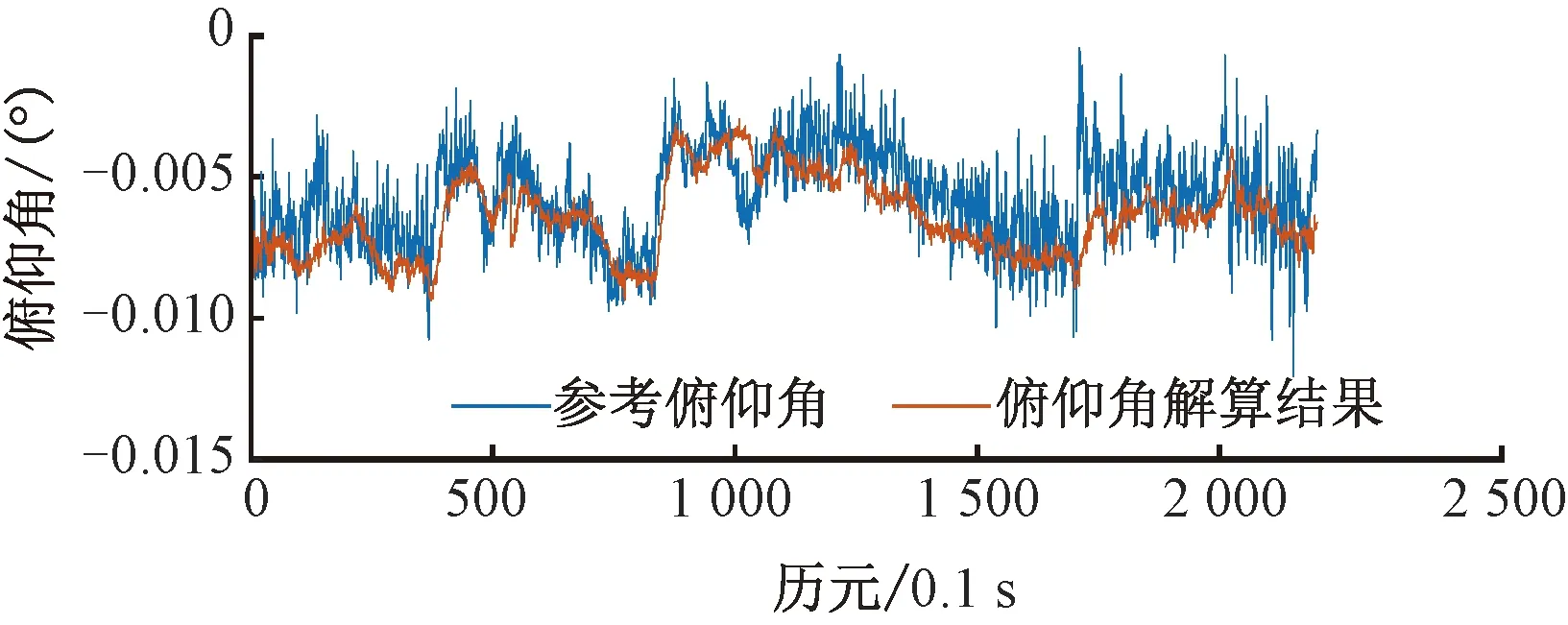
图15 俯仰角结果对比(实验二)
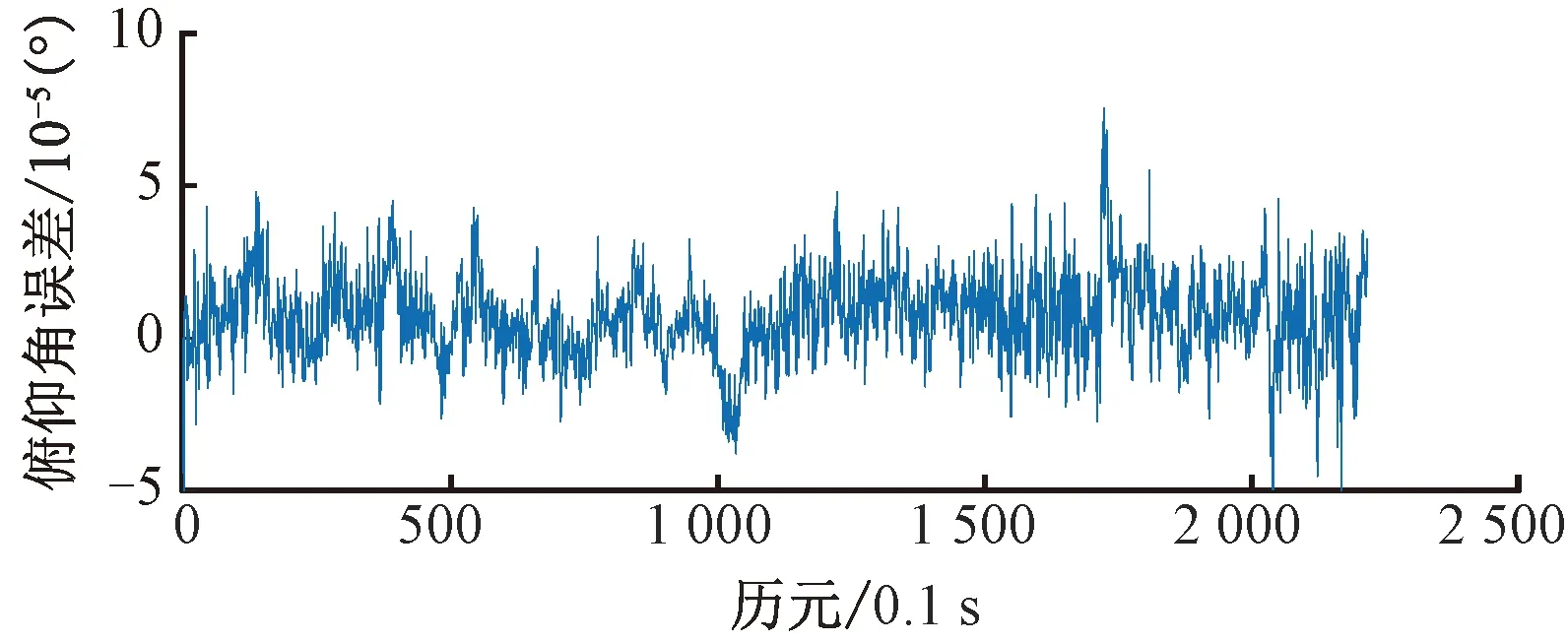
图16 俯仰角结果误差(实验二)
表1对实验一和实验二的偏航角、俯仰角的误差进行统计分析,其中实验一偏航角的误差均方根为0.118 5°,俯仰角由于其本身变化范围较小,因此其误差均方根保持在0.001 6°。实验二的偏航角误差均方根为0.160 1°,俯仰角的误差与实验一近似。

表1 偏航角与俯仰角误差分析 (°)
将实验一与实验二对比可以看出尽管实验二的卫星信号质量更好,但由于列车运行速度较低,其解算得到的偏航角误差均方根比实验一大0.05°左右。且在实验二中,列车在转向的过程中对偏航角解算结果影响更大。这是因为列车的速度会影响时间差分过程中的位移矢量的方向,当列车运行速度较慢,且有较大幅度转向时,位移矢量的方向列车实际偏航角的方向会产生小范围偏差,由此可见列车速度对单天线时间差分的测姿算法精度有一定的影响,具体表现在速度越高,其姿态解算精度越高。但从整体姿态解算结果来看,误差值保持在1°以内,可以用于辅助判断列车的轨道占用状态。
5 结论
为进一步提高道岔区段轨道占用识别准确性,本文引入列车姿态角作为辅助判断的手段,提出一种单天线列车姿态解算方法,采用时间差分与星间差分相结合的“双差”技术,在保证精度的前提下避免了复杂的误差修正模型以及整周模糊度估计。利用卡尔曼滤波算法对列车位移矢量估计解算,并根据此位移矢量求解列车姿态。为了评估所提出的单天线测姿算法性能,选取青藏线上的两组真实列车数据进行实验仿真,其中偏航角的误差均方根可以分别达到0.118 5°和0.160 1°,俯仰角误差均方根分别为0.001 4°和0.001 6°,同时,通过对比结果分析得出列车速度会影响单天线测姿算法精度。

