基于三角模糊数的城市轨道交通应急救援中心不确定性选址研究
张 岚,董宝田,寇淋淋,王艳辉
(1.北京交通大学 交通运输学院, 北京 100044;2.北京市地铁运营有限公司, 北京 100044)
随着我国城市轨道交通持续高速发展,截至 2021 年底,中国大陆地区共有 50 个城市开通城市轨道交通运营线路 283 条,运营线路总长度 9 206.8 km,全年累计完成客运量236.9 亿人次[1]。2021年全国有24个城市的线网规模达到100 km以上,我国城市轨道交通正逐步实现大规模网络化运营。但网络规模越大、偶发故障和突发事件发生的概率越大,合理设置应急救援中心位置,确保应急响应效率,成为有效控制应急事件影响范围和影响后果的重中之重。
国内外对应急救援中心选址问题研究众多,主要有P-中心模型、P-中位模型、覆盖选址模型及相应的扩展模型[2-4]。P-中心也叫Minmax问题,解决任意一需求点到距离该需求点最近的供给点最大距离最小的问题。P-中位问题以供应点和需求点距离与需求量乘积最小为目标,解决P个供给点选择问题。集覆盖和最大覆盖问题是覆盖问题的两大分支。在满足覆盖所有需求点的前提下,集覆盖重点解决供给点的总建设数量或建设费用最小的问题,多用于消防中心和救护车等应急服务设施的选址问题。
牟海波等[5]针对铁路应急物资的储备点选址问题,建立以铁路应急物资储备点的运输能力和应急物资需求点的需求为约束的双目标规划模型;汤兆平等[6]建立以资源调度时间最短和应急费用最低为优化目标的多目标规划模型,并利用模糊理论方法解决不确定性需求问题。毛保华[7]以城市居民出行分布及出行时间分布为约束,研究铁路客运站最优设置问题及分工问题。曹琉等[8]在综合考虑最短路径、建设费用等要素的基础上,建立网络化应急救援基地选址模型。马斌军[9]建立3种不同线网发展状态的应急救援选址优化模型,包括发展中线网选址模型、成熟线网新选址模型和成熟线网新增选址模型。祝蕾[10]将城市轨道交通网络视为复杂网络,在选址模型中引入节点脆弱性分析,并提高了脆弱性高站点的覆盖水平。聂鑫路等[11]以应急救援需求概率和应急救援时间为影响要素,以应急救援站数量最少为目标,建立粒子维度自适应模型,并提出滚动式多步求解方法。
既有应急救援基地选址模型大多以建设成本、距离、平均到达时间等作为目标和约束条件,但未充分考虑线路客流情况、线路风险程度、线网规划等要素。本文在充分考虑上述因素的基础上,用三角模糊数直觉模糊集方法表征计算路径权值,并建立双层规划模型,在建设成本满足和路网全覆盖的情况下,优化多级应急救援点位置,减少建设成本,缩短应急救援时间,提升应急响应效率,降低突发事件影响。
1 应急救援中心选址问题描述
城市轨道交通坚持“第一时间开通正线运营”的理念组织应急处置工作,除极端自然灾害外,极少发生双向线路同时中断的情况。因地面交通持续拥堵、救援器材进出站不便等客观限制,利用城市轨道自身线网进行应急物资调运具有相当的便利优势,成为城轨应急救援的必要手段。由列车故障和设备设施故障引起的突发事件,一般由司机和现场工作人员利用现场资源进行先期处置,相关技术人员和抢险物资尽快增援。如需清客救援,则由后续列车在线路区间连挂、牵引或推行至车辆段。单向线路中断的情况下,一般由对向线路运送人员和物资。
综合来看城市轨道交通应急救援中心选址问题是网络应急需求引发的全局最优化问题。本文认为,除常规的数量最少、全覆盖、到达时限等最优化目标外,其时间最短原则不是应急救援中心至各个车站的平均时间最短,而是在整体最优的基础上,中心至每个车站的救援时间最短。除此之外,应急救援基地的选择不仅要考虑近期需求,还应该做战略性长远考虑。
2 城轨应急救援中心选址模型
2.1 模型假设
(1)城市轨道路网具备网络化运行能力,且未发生双向线路同时中断情况。
(2)应急需求趋于抽象的城市轨道路网站点及线路区间。
(3)应急救援基地备选点为抽象的城市轨道路网车站和车辆段。
(4)车站和车辆段作为救援基地具有不同的覆盖半径。
(5)同一线路区间同一方向的平均客流量相同。
2.2 地铁应急救援中心选址模型
为有效展示网络内线路之间的连接关系、明晰网络结构,将城轨路网抽象为网络,见图1。
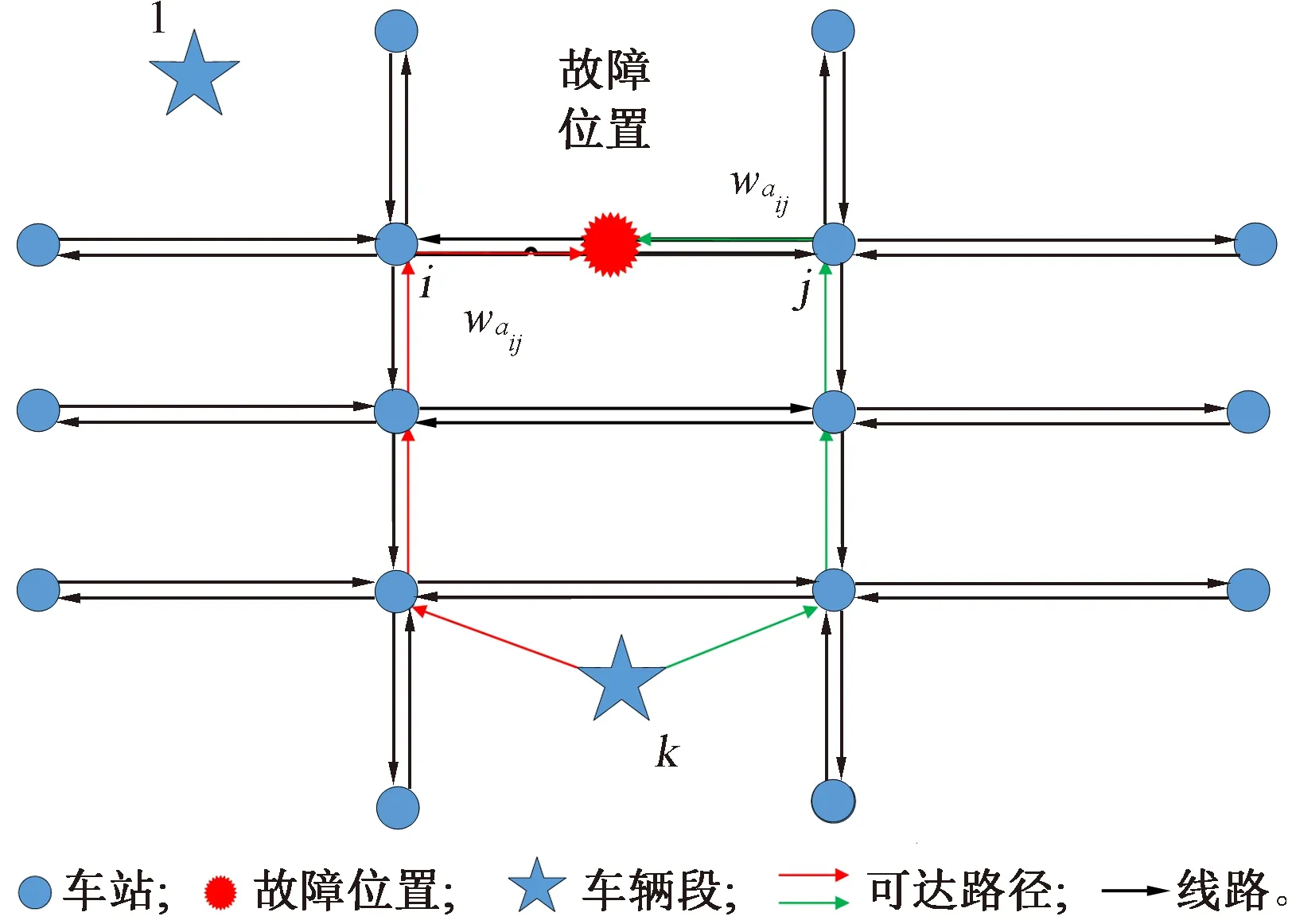
图1 城轨路网抽象网络
G=(V,A,W)为给定的城轨路网,变量符号及含义见表1。
救援基地候选点vk从i点对弧段aij覆盖率为
( 1 )

表1 城轨路网信息变量符号及含义
则在节点集V设置的救援基地弧段aij的覆盖比例Caij为
( 2 )
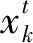
救援基地vk对弧段aij的覆盖水平为
( 3 )
应急救援基地选址问题主要分为两部分:①确定应急救援基地的位置和数量;②明确划分救援区域。因此,采用双层规划模型解决选址问题。
双层规划具有二层递阶结构,目的在于解决双层决策系统优化问题,上层规划给定的决策变量,是下层规划的参量,在满足既定目标函数和约束条件基础上求下层规划最优解,并反馈给上层规划,以求得整体上的最优解。
(1)下层模型
将应急救援基地的位置作为决策变量,在应急救援基地覆盖城轨路网的情况下,以城轨路网损失最小为目标函数,使得应急救援基地对城轨路网的覆盖度最高,路网失效损失最低。
( 4 )
( 5 )
0≤Caij≤1
( 6 )
( 7 )
( 8 )
( 9 )
(10)
(2)上层模型
确定各应急救援基地的服务范围,Sk,aij为第k个候选点是否覆盖弧段aij,即
(11)
考虑在确定服务范围时,尽可能使每个弧段距其所属的应急救援基地的距离最短并且客流影响最小,Sk,aij为决策变量,目标函数为需求点到应急救援基地最小加权距离。
约束条件为每个弧段至少有1个应急服务基地覆盖,每个应急服务基地至少服务1个弧段。同时,限制应急服务基地和其服务弧段在其最大覆盖半径之内。
第k个应急救援基地到弧段aij的最短路径加权距离dk,aij为
dk,aij=min{|d(k,i)|·l(k,i),|d(k,j)|·l(k,j)}+
daij·laij
(12)
综上,构造上层模型为
(13)
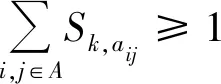
(14)
(15)
(16)
3 城轨应急救援中心选址模型求解
城轨应急救援中心双层规划模型基本流程见图2。

图2 城轨应急救援中心选址模型求解过程
城轨应急救援中心选址模型主要包括4个步骤:应急救援中心选址建模,计算路径权值,搜索最短路径,求双层规划模型最优解。其中,路径权值与平均断面客流量、实际物理长度、路径风险程度相关,根据线路区间实际数据测得。上述3要素权重采用专家评分法基于三角模糊数直觉模糊集确定,以最大可能地消除主观影响。由于城市轨道交通线网供需点极多,最短路径搜索采用A-Star算法在路径权值基础上搜索予以明确。双层规划模型采用差分进化算法求解。
3.1 路径权值计算
|d(k,i)|与路径上的平均断面客流量、实际物理长度、路径风险程度有关,路径的权值与3要素的归一化后的数值及其权重相关,而3要素权重取决于其重要度。本文设计了三角模糊数直觉模糊集来表征专家对三要素重要度的评判意见,并通过去模糊化得到最终权重分配。
(17)
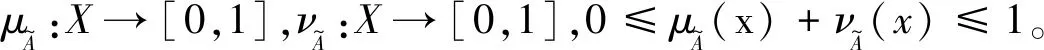
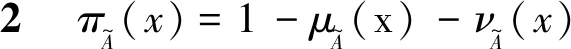
定义3三角模糊数a=(al,am,ar)的隶属度函数μa:X→[0,1]为[12]
(18)
式中:隶属度函数μa(x)∈[0,1],0≤aleft≤amedium≤aright≤1;amedium为模糊数a的重心。
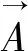
(19)
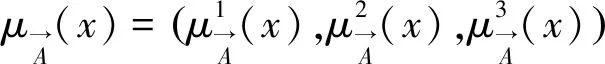
本文将重要度分为5级,其对应的三角模糊数直觉模糊集见表2、图3。
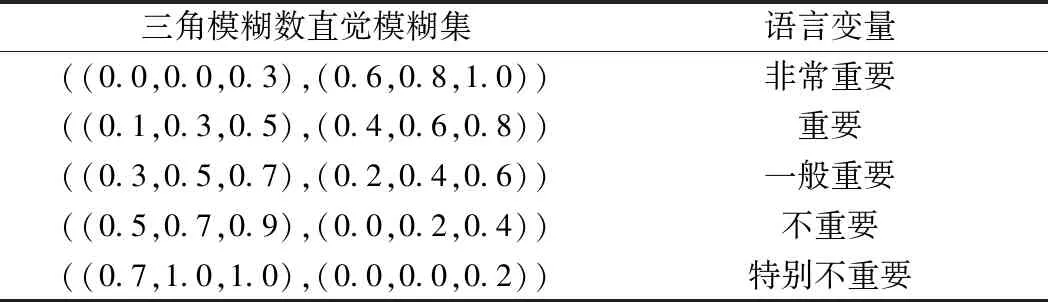
表2 重要度级别及其对应的
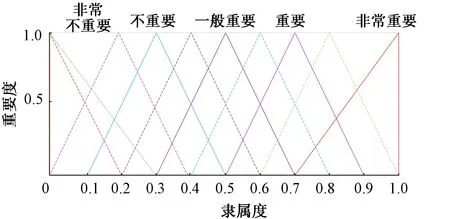
图3 重要度分级
计算出各要素重要度权重后,根据归一化的数据,计算路径权值。
3.2 最短路径搜索
A-Star算法以Dijkstra算法和最佳优先算法为基础,采用启发函数估价全局信息,作为路径节点实际耗费代价的辅助评判机制,完成最佳路径规划。城轨路网较为庞大,需求路段、车站、车辆段节点数量非常多,因此采用A-Star算法寻找最短路径,以确保算法效率和求解准确性。
算法主要表达式为
f(η)=h(η)+g(η)
(20)
式中:f(η)为初始状态经过状态η到达目标状态的估价;g(η)为初始状态达到状态η的实际耗费;h(η)为状态η到达目标状态的最低估价。
在A-Star算法中,最短路径规划问题为在赋权有向图中找出两个起始点与目标点之间权重之和最小的路径。将路网环境中的拓扑关系改记为赋权有向图,图中任一路径记为Path=(aij,aj,j+1,aj+1,j+2,…,aj+s-1,j+s),路径总长度为每个分段路径的长度之和W(Path)=waij+waj,j+1+waj+1,j+2+…+waj+s-1,j+s,即最短路径被定义为求解有向图中的起始点与终点之间的min(W(Path)A)。此处选择欧式距离函数Dis来表示节点间的距离。
Dis=|d(i,j+s)|
(21)
具体计算步骤如下:
Step1初始化,生成OPEN和CLOSED列表,并将起始点的信息载入OPEN列表,记做f(η)=h(η)。
Step2在OPEN列表中查找,若未查到数值,则转Step1,继续寻找起始节点;若在OPEN列表内查到数值,代表已经加在路径规划的目标节点,则执行Step3。
Step3计算OPEN列表中的f(η)值,将所有节点f(n)值中的最小点作为最佳节点B-Node,载入CLOSED列表中,并以该节点为当前节点,转Step4。
Step4根据估算函数判断最佳节点是否为路径目标点。如果是,那么算法结束,输出规划路径节点;若不是,将当前节点的邻近节点载入OPEN列表,执行Step2。依次循环,直至找到规定的目标节点。
Step5在CLOSED列表中保存最佳节点,输出最终规划路径。
3.3 模型求解
差分进化算法实施随机、并行、直接的全局搜索,是当前求解双层规划问题最有效的进化算法之一,其基本步骤如下:
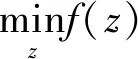
[Xmin,Xmax]为变量搜索空间,其值域为
Xmin=(xmin1,xmin2,…,xminD)
(22)
Xmax=(xmax1,xmax2,…,xmaxD)
(23)
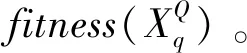
(24)
Step2变异。在差分进化算法中,每个差分矢量由第Q代中两个不同的父代个体交叉组成,表示为
Dr1,2=xr1(Q)-xr2(Q)
(25)
式中:r1、r2为不同个体的索引。
对于目标矢量Xq(Q),其变异行为表示为
Vq(Q+1)=xr3(Q)+F×Dr1,2
(26)
式中:r3为另一个个体的索引。
若Vq(Q+1)不在值域范围内,则可令Vq(Q+1)=Xmin+rand(0,1)×(Xmax-Xmin)。r1,r2,r3∈{1,2,…,NP},NP≥4且互不相等,F⊂[0,2]。
变异机制为
(27)
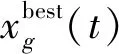
Step3交叉操作,提高种群多样性。试验个体Uq(Q)=(uq1,uq2,…,uqD)由当前个体Xq(Q)与对应的变异个体Vq(Q)交叉生成。
(28)
式中:o=1,2,…,D。
首先通过随机选择确保Uq(Q+1)至少由一个Vq(Q+1)贡献,再由CR决定具体哪个由Vq(Q+1)贡献,哪个由Xq(Q+1)贡献。交叉概率CR在初始化时预先设置,CR∈[0,1]。CR越大,Vq(Q+1)对Uq(Q+1)的贡献越大,当CR=1时,Vq(Q+1)=Uq(Q+1),算法局部搜索能力增强,算法收敛加快;反之,CR越小,xq(Q)对Uq(Q+1)贡献越多,当CR=0时,xq(Q)=Uq(Q+1),算法全局搜索能力提升,种群多样性增加。6个基因位的“染色体”交叉操作过程见图4。
图4 交叉过程示意
Step4选择操作。经变异和交叉生成的候选个体Uq(Q+1)与xq(Q)基于“贪婪选择”搜索机制开展竞争,哪个最优则哪个成为新子代,操作方程为
xq(Q+1)=
(29)
式中:fitness为适应度函数,用来判断Uq(Q+1)和Xq(Q)的优劣。
4 实例分析
以北京城市轨道交通为例,建立应急救援基地选址模型。首先对北京城市轨道交通路网进行抽象,为确保应急救援基地对未来线网规划的可用性,以未来线网规划为依据,选择北京城市轨道交通路网抽象网络拓扑图,见图5。该路网中共有579座车站,541段弧,其中红色圆点为现有应急救援中心位置,共36个。
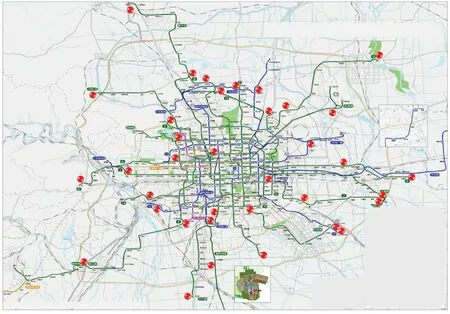
图5 北京城市轨道交通路网图
应急救援中心建设一般基于既有建筑空间,无建筑物建设成本,总建设成本简化为应急救援物资配属成本。根据既往不同等级应急救援中心物资配备情况,高等级救援中心配备标准是较低等级救援中心配备标准的2倍,因此认为车辆段应急救援中心建设成本是车站应急救援中心建设成本的2倍。假设建设位于车辆段的应急救援中心点为一级基地,建设成本为2单位,权重距离的覆盖半径为100;建设位于车站的应急救援中心点为二级基地,建设成本为1单位,权重距离覆盖半径为50;需要覆盖率达到100%以上,即β=1.00。设置差分算法的种群规模NP=100,矢量缩放因子F=0.5,交叉概率CR=0.8,最大迭代次数max_iter=100 000。
统计北京城市轨道交通某时段(2017年11月8日)1号线各区段权值见表2。以苹果园—古城路上行区间为例,平均断面客流量807.5人,平均故障率18%(百万车公里事故发生率)以5 min延误控制指标为主,区间长度2 606 m,将上述3要素归一化后按照三角模糊数直觉模糊集方法,计算得到该苹果园—古城路上行区间权值为3.48。
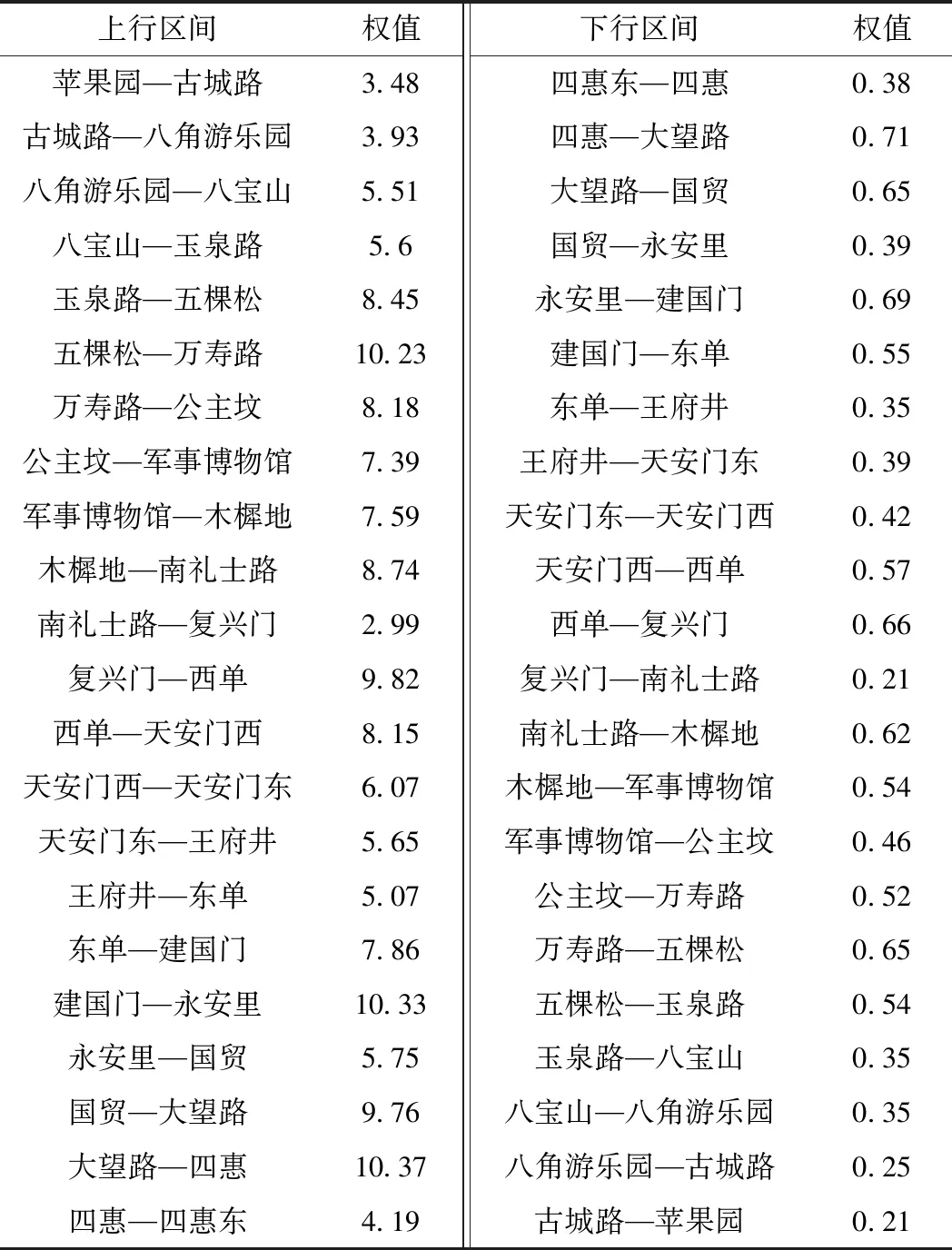
表2 1号线线路区段权值
对应急救援基地选址模型进行求解,得到最优方案,见图6。规划建设27个应急救援基地,其中,一级应急救援基地10个,分别位于回龙观车辆段、马泉营车辆段、万柳车辆段、太平湖车辆段、四惠车辆段、五里桥车辆段、宋家庄车辆段、马家堡车辆段、郭公庄车辆段、土桥车辆段;二级应急救援基地17个,分别位于阎村车辆段、高米店南、瀛海车辆段、次渠车辆段、七里庄站、苹果园站、西钓鱼台站、金融街站、张自忠路站、广渠门外站、政务中心东站、东坝车辆段、西坝河站、马连洼站、大屯路东站、后沙峪站、南邵站。
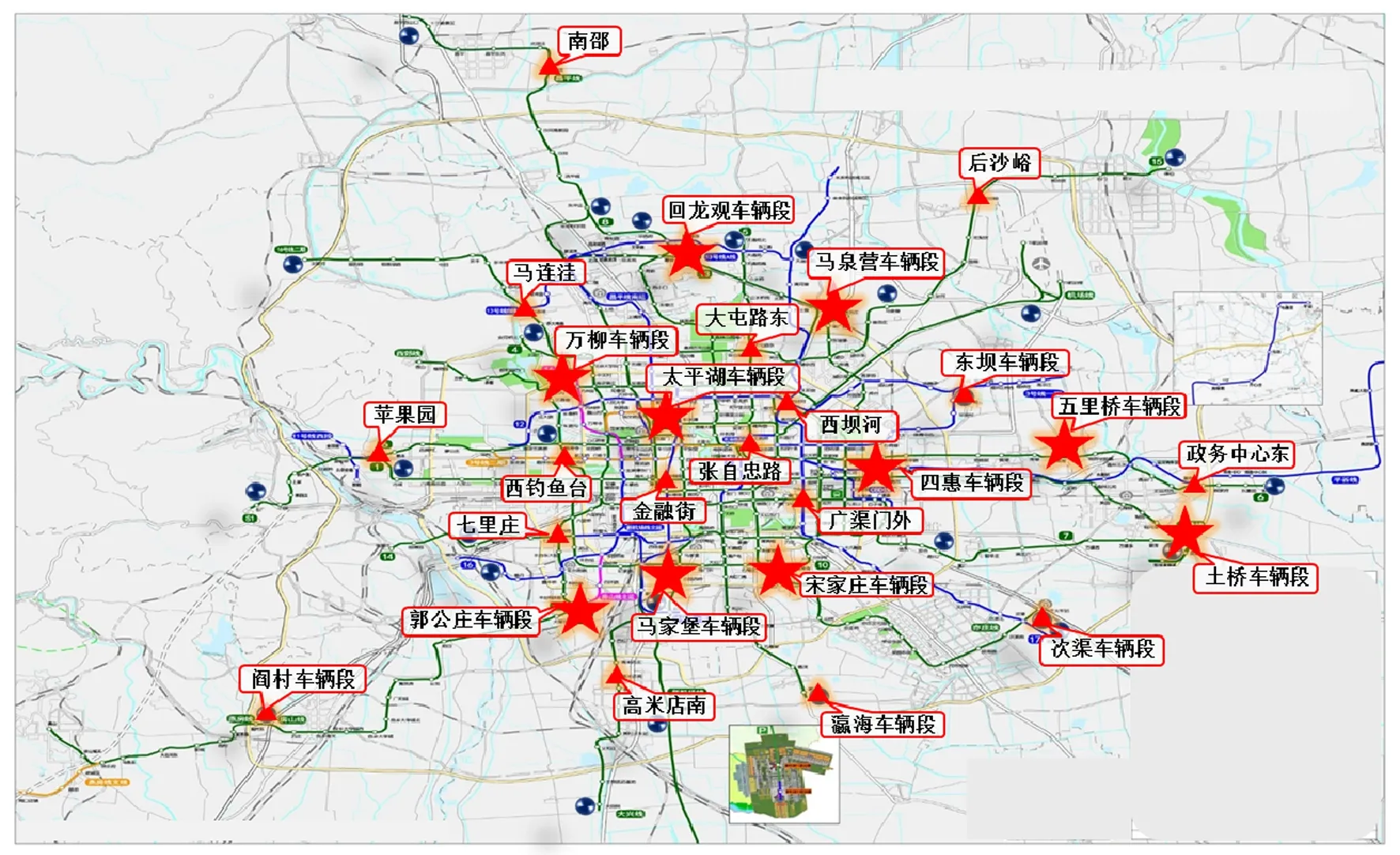
图6 应急救援基地选址模型所提方案
原应急救援中心方案共36个应急救援点,其中车辆段15个,车站21个,总建设成本为51单位。在路网全覆盖的情况下,本文所提建设方案总建设成本为37个单位,总成本减少超过27%。
5 结论
城市轨道交通线网应急救援基地选址问题,要求线网全覆盖,救援时间最短(非平均救援时间),救援路径的选取也要尽可能地降低对正常运营的影响。本文以网络化运行的城轨网络为研究对象,将城轨线网中具备条件的车站和车辆基地作为应急救援基地的不同级别的备选点,基于加权有向网络图的双层规划模型,以应急救援基地对城轨路网的覆盖度最高,路网失效损失最低,尤其是基地到各车站的整体时间最短为目标建立上层规划,下层规划则在确定服务范围时,以应急救援基地的距离最短并且客流影响最小为目标。其中A-star算法求解了基地到需求点的最短路径,差分进化算法则对双层规划模型进行了求解。本文所提算法明确了城市轨道交通线网内的应急救援基地位置,为应急预案的编制提供了技术支撑。
但城市轨道交通网络运行条件不同、各线路特性不同、风险类型和风险程度也不尽不同,应急救援基地不仅要分级,还需要分类设置。因此,本文的方法与目前城轨实际运营情况仍有待进一步结合,还需对应用条件进行优化,对救援基地进行精细化分类,按线路具体风险情况进行设置,以更符合实际应用。

