基于种群分区的多策略自适应多目标粒子群算法
张伟 黄卫民
在多数实际问题和工程应用中,决策者需要同时使多个目标在决策空间内尽可能得到最佳优化,即多目标优化问题(Multi-objective optimization problems,MOPs)[1].在MOPs 中,使算法快速有效地收敛在Pareto 最优解集中并使得到的非支配解在Pareto 前沿中保持均匀分布是衡量多目标优化算法性能的重要指标之一,即算法的收敛性和多样性.过度强调算法的收敛性会导致粒子聚集,陷入局部最优;过度增强算法多样性会导致算法收敛速度慢,影响最终非支配解集的收敛性[2].因此,平衡算法的收敛性和多样性是研究MOPs 的重要课题之一[3−5].
粒子群优化算法因为易于实现和计算效率高等特点,在单目标优化问题上得到广泛应用.当粒子群优化应用于多目标优化问题时,即多目标粒子群优化(Multi-objective particle swarm optimization,MOPSO).由于MOPs 中没有真正意义上的最优解,所以MOPSO 算法的全局最优粒子gbest和个体最优粒子pbst需要采取特定的策略进行选取,并且由于MOPSO 算法较快的收敛速度,在算法学习过程中,易使所得到的非支配解集迅速丧失多样性[6].
为解决上述问题,学者们相继提出了一些改进的MOPSO 算法.Coello等[7]提出一种基于自适应网格的多目标粒子群优化算法,采用自适应网格技术对外部存档进行维护,指导粒子更新,并对粒子以及粒子的飞行区域实施变异.虽然算法相比于传统多目标进化算法在MOPs 问题上表现出一定优势,但在解决多局部前沿的复杂MOPs 问题时存在困难,且非支配解多样性较差.Raquel等[8]提出一种基于拥挤距离的MOPSO (An effective use of crowding distance in MOPSO,cdMOPSO)算法,采用目标空间的拥挤距离评估非支配解的密集程度,并据此来选取全局最优粒子和保持外部存档中解的分布性,但算法仍存在收敛性不足的问题.为解决这个问题,Yen等[9]提出一种动态多子群的多目标粒子群优化算法,算法将种群分为多个子群,通过动态调整子群大小从种群角度平衡算法的探索能力和开发能力,实验结果表明算法性能得到改善.
与上述通过支配关系确定搜索机制的MOPSO 算法不同,Peng等[10]基于分解的多目标进化算法 (Multi-objective evolutionary algorithm based on decomposition,MOEA/D) 的分解框架,将MOPs 分解为多个单目标优化问题,用粒子群优化的搜索方法替代遗传算子,从而提出一种MOPSO算法,虽然其维护了一个外部存档存储各单目标优化问题的全局最优粒子,但并未对粒子群优化的搜索机制进行优化,算法综合性能不足.Martinez等[11]提出一种多目标粒子群优化器,算法提出了一种重新初始化策略来保持群的多样性,当粒子存在超过一定代数时将会重新初始化,以此来提高种群多样性和避免陷入局部极值,但由于用分解替换了占优关系,算法在求解一些复杂MOPs 时,不能覆盖整个Pareto前沿.为解决这个问题,Dai等[12]提出一种基于分解的多目标粒子群优化算法,根据一系列预先定义的方向向量将整个目标空间分解为一系列子空间,并让每个子空间都有至少一个解来维护解集的多样性,进一步提升MOPSO 算法解决MOPs的能力.
学者们还提出了其他改进方法提升MOPSO算法的性能.Hu等[13]提出一种基于平行单元坐标系的自适应多目标粒子群优化(Adaptive MOPSO based on parallel cell coordinate,pccsAMOPSO)算法,将目标空间的Pareto 前沿变换为平行单元坐标形式的二维网格,采用种群的熵作为反馈信息,设计具有自适应调节探索和开发过程的进化策略,使算法的收敛性和多样性都得到了提升.Kumar等[14]提出一种自学习的多目标粒子群优化算法,在粒子速度和位置更新上采用4种运算方式,不同方式对应不同的学习来源,独立提高每个粒子搜索的有效性.但目前多数改进的MOPSO 算法仅依靠一种搜索策略更新粒子的位置和速度,没有考虑不同性能粒子的搜索情况,在求解复杂多目标问题时,算法收敛性和多样性不足.
为解决上述问题,进一步提升MOPSO 算法的性能,本文提出一种基于种群分区的多策略自适应多目标粒子群优化(Multi-strategy adaptive multiobjective particle swarm optimization based on swarm partition,spmsAMOPSO)算法.对MOPSO 算法的改进在于: 1)提出一种基于种群分区的多策略全局最优粒子选取方法,并基于种群分区思想,提出一种多策略的变异方法,提升粒子探索和开发能力;2)为提升个体最优粒子选取的可靠性,提出一种带有记忆区间的个体最优粒子选取方法;3)根据算法环境,自适应调整粒子探索和开发过程,并采用双性能测度的融合指标维护外部存档,平衡算法的收敛性和多样性.实验结果表明,相比一些其他多目标优化算法,本文算法在收敛性和多样性上具有一定优势.
1 多目标优化问题和粒子群优化算法
1.1 多目标优化问题
多目标优化问题的数学模型可描述为:
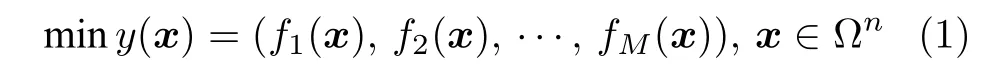

则称x′为Pareto 最优解.
3) Pareto 最优解集: 对给定的MOPs,Pareto最优解集定义为:
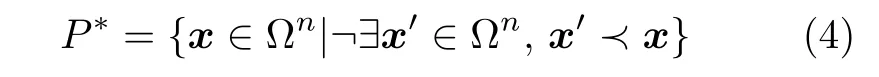
4) Pareto 前沿: 由P∗的定义,Pareto 前沿(Pareto front,PF)可定义为:
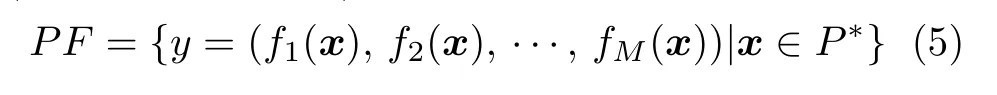
1.2 标准粒子群算法
粒子群算法是由Kennedy等[15]提出的一种基于种群搜索的进化计算技术.种群中粒子i的速度vi和位置xi的更新方法分别为:

2 基于种群分区的多策略自适应多目标粒子群优化算法
MOPSO 算法因其特殊的搜索机制和快速的收敛速度,需要对算法的参数调整、全局最优粒子选取、个体最优粒子选取、外部存档维护以及粒子变异操作等部分制定策略以引导粒子搜索[7].本文在全局最优粒子选取和变异操作部分,提出一种基于种群分区的多策略改进方法,并提出一种带有记忆区间的个体最优粒子选取方法,结合自适应参数调整以及使用融合指标的外部存档维护策略,进一步提升MOPSO 算法性能.本文spmsAMOPSO 算法的整体结构如图1 所示,通过算法的参数调整、最优粒子选取、变异以及外部存档维护等部分之间的协同,共同指导粒子寻优过程,提升算法综合性能.
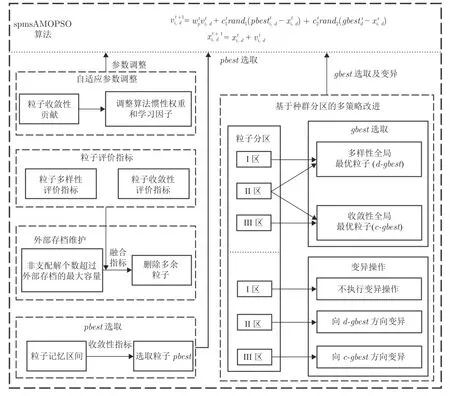
图1 spmsAMOPSO 算法整体框图Fig.1 Frame of spmsAMOPSO algorithm
2.1 自适应调整惯性权重和学习因子
对于MOPSO 算法,由于算法迭代过程中,其环境是实时变化的,为提升粒子探索和开发能力,本文根据算法环境变化调整惯性权重wp以及学习因子c1和c2,达到算法参数精细化调控的目的.
当算法搜索到的非支配解需要加入外部存档时,计算其对外部存档中解的支配程度,得到粒子的收敛性贡献[16]:
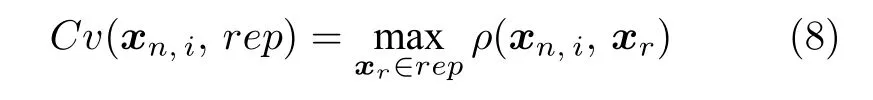
式中,xn,i为算法寻优所得到的第i个非劣解;xr为外部存档中存储的非支配解;rep为算法外部存档;ρ(xn,i,xr)为xn,i对xr的支配程度,计算方法如下:
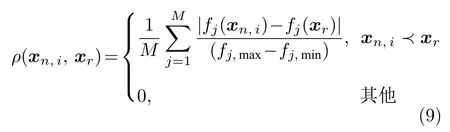
式中,M为目标个数;fj,max和fj,min分别为外部存档中非支配解在第j个目标上的最大值和最小值.若t时刻算法搜索到np个非支配解,则算法的环境检测参数Ap定义为:
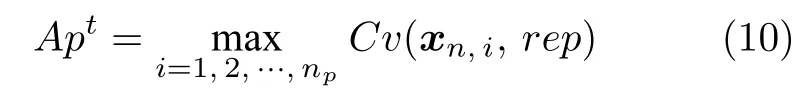
粒子对外部档案的收敛性贡献反映算法当前的收敛状态,当Ap较大时,种群处于探索阶段,应保持其全局搜索能力,随着Ap逐渐减小,种群逐渐达到收敛,应加强局部搜索,当Ap趋于0 时,表明种群达到收敛稳定状态.
由文献[17]可知,较小的惯性权重wp和学习因子c1以及较大的学习因子c2有利于算法收敛,较大的wp和c1以及较小的c2有利于增强算法多样性.为避免参数调整影响算法搜索连贯性,本文采用增量式参数调节方法:
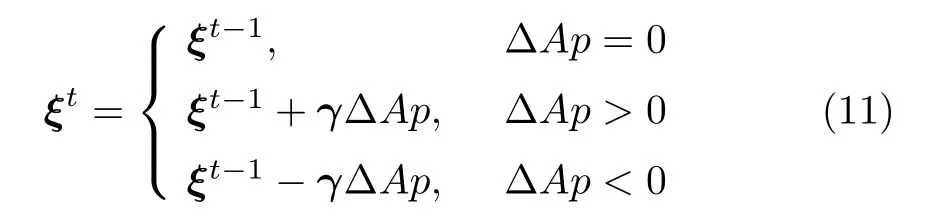

2.2 基于种群分区的多策略全局最优粒子选取
全局最优粒子 (gbest) 选取是影响MOPSO 算法收敛性和多样性的重要问题.本文采用不同的评价指标分别选取促进算法收敛的全局最优粒子(cgbest)和增强算法多样性全局最优粒子 (d-gbest),并根据粒子性能将种群划分为多个区域,对不同区域粒子制定不同的gbest选取策略.
2.2.1 c-gbest和d-gbest 的选取方法
为保证算法的收敛性,在算法寻优过程中选取外部存档中收敛程度最好的粒子做为算法的cgbest.
本文采用粒子的平均排名和全局损害作为粒子的收敛性评价指标.
粒子平均排名(Average ranking,AR)的计算方法为:
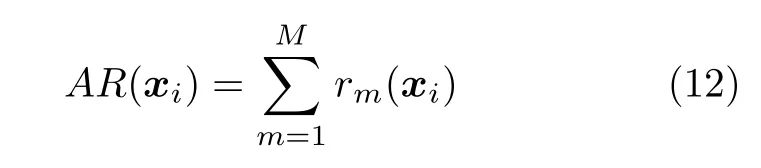
式中,rm(xi) 为粒子i在第m个目标变量上的排名;M为目标个数.
粒子全局损害(Global detriment,GD)的计算方法如下:
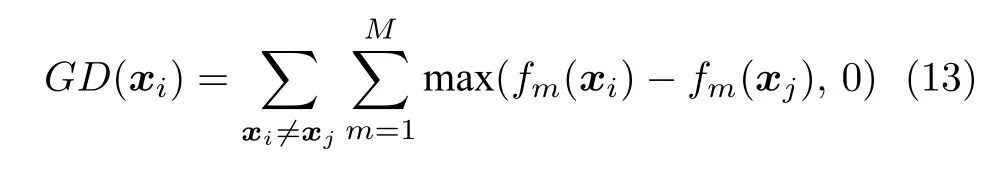
式中,fm(xi) 为粒子i在第m个目标上的适应度值;GD(xi) 表示粒子i比其他粒子在目标上的劣势.
由于通过AR 指标选取最优粒子时容易使粒子聚集在Pareto 前沿的边缘,而GD 指标容易排除Pareto 前沿中的端点粒子[6].将上述两个指标结合,改善评价方式缺陷:
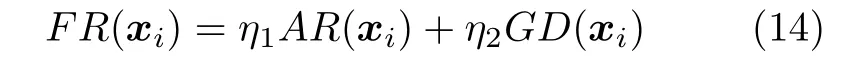
式中,η1和η2为区间[0,1]之间的常数,用于确定指标AR和GD 的权重,其取值分别为:η1=0.4、η2=0.6,具体讨论分析见第3.2.1 节.Fusion ranking (FR)指标有利于目标解的序列和个体之间的相对信息结合,从而更全面地评估解空间内个体的收敛程度.由式(12)~(14)计算外部存档中各粒子的融合排序FR 指标,选取FR 指标最小的粒子作为算法的c-gbest.
为保证非支配解集的多样性,在算法寻优过程中应引导粒子向外部存档中非支配解较为稀疏的区域飞行,本文采用粒子的拥挤距离作为算法多样性全局最优粒子(d-gbest)的选取标准.
粒子i与粒子j之间的欧氏距离为:
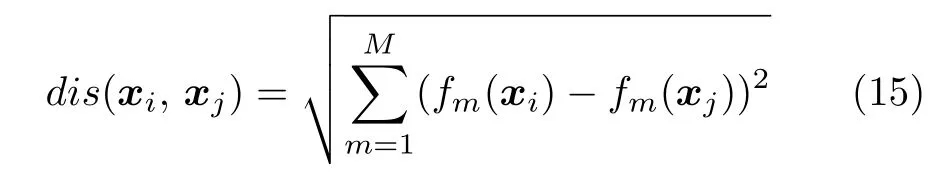
为避免个别极端粒子影响粒子密度估计,本文采用局部距离作为粒子的密度评价指标,取粒子i距离最近的S个粒子之间距离的平均值作为粒子i的拥挤距离,即:
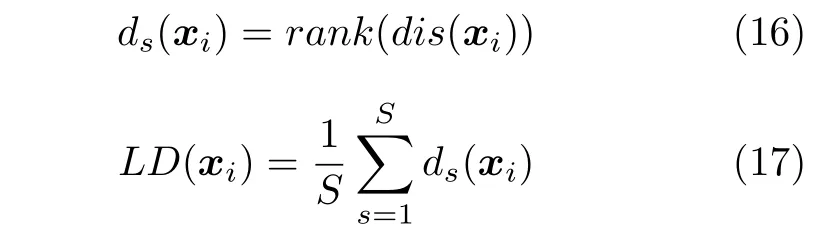
局部拥挤距离(Locality crowding distance,LD)为反映粒子分布情况的指标,粒子的LD 指标越大,表明粒子分布越稀疏.根据式(15)~(17)计算外部存档中各粒子的LD 指标,选取LD 指标最大的粒子作为算法的d-gbest.
2.2.2 种群分区及各区域粒子的 gbest 选取方法
为增强粒子探索和开发能力,并根据算法环境自适应调整种群探索和开发过程,扩大粒子搜索区域的同时保持算法收敛性和多样性的平衡.本文通过粒子收敛程度将种群中粒子划分为3 个区域,根据不同区域粒子的特征,提出一种多策略的gbest选取方法.
根据种群中各粒子的FR 指标大小,得到每个粒子基于指标FR 的种群内排名:
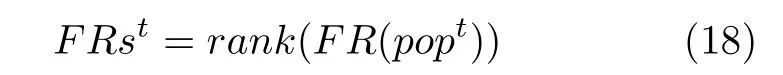
根据每个粒子的群内排名FRs,确定各粒子的所属区域:
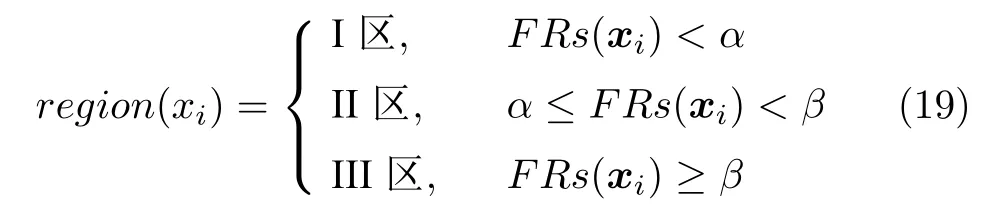
式中,α和β均为正常数,通过确定α和β的值,将种群划分为3 个区域,分区参数选取分别为:α=0.2N,β=0.8N,N为种群粒子个数,分区参数的取值对算法影响分析见第3.2.2 节.图2 给出了种群各区域粒子的划分情况.
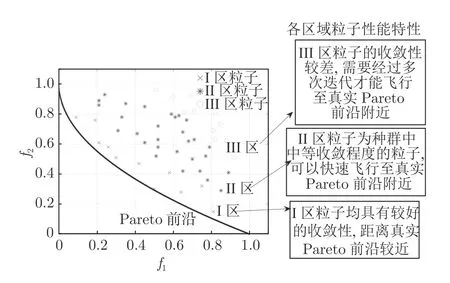
图2 种群中各粒子所属区域Fig.2 Location of each particles in the population
根据各区域内粒子的不同特征,制定一种多策略的gbest选取方案:
1)对于I 区粒子,其在种群中具有较好的收敛性,为保持算法搜索到非支配解的多样性,使I 区粒子选取d-gbest作为全局最优粒子指导其飞行.
2)对于II 区粒子,为平衡算法的收敛性和多样性,使种群能够探索更多区域,使II 区粒子根据算法环境进行全局最优粒子的选取,由第2.1 节中的粒子收敛贡献度对算法当前环境进行估计,根据算法环境确定粒子选取c-gbest或d-gbest作为gbest的概率:

由式(20)使II 区粒子能够根据算法当前环境进行自适应探索和开发.当Ap较大时,为保证算法收敛性,使粒子有较大概率选取c-gbest作为gbest指导其飞行;当Ap逐渐减小时,为增强算法的多样性,应使粒子有较大概率选取d-gbest作为gbest.
3)对于III 区粒子,由于其在种群中性能较差,对种群中的其他粒子的飞行没有太大贡献,为提升粒子的开发能力,保证算法收敛性,使III 区粒子选取c-gbest作为全局最佳粒子指导其飞行.
通过上述多策略的gbest选取方法,使算法能够根据不同区域的粒子性能和算法环境,选取c-gbest或d-gbest作为全局最优粒子,有效提升算法的收敛性和多样性,增强粒子探索和开发能力.
2.3 基于种群分区的多策略高斯变异
由于MOPSO 算法具有快速的收敛过程,算法易发生早熟收敛,过早结束搜索过程,陷入局部最优.为解决这个问题,在粒子位置更新时,对部分粒子加入扰动,使算法跳出局部最优,扩大粒子搜索区域[19].基于种群分区,针对不同区域粒子的性能,提出一种多策略的变异方法:
1)若粒子i位于I 区,表明粒子i距离真实Pareto前沿较近,为避免种群产生退化,保留种群中的精英个体,粒子i不进行变异操作;
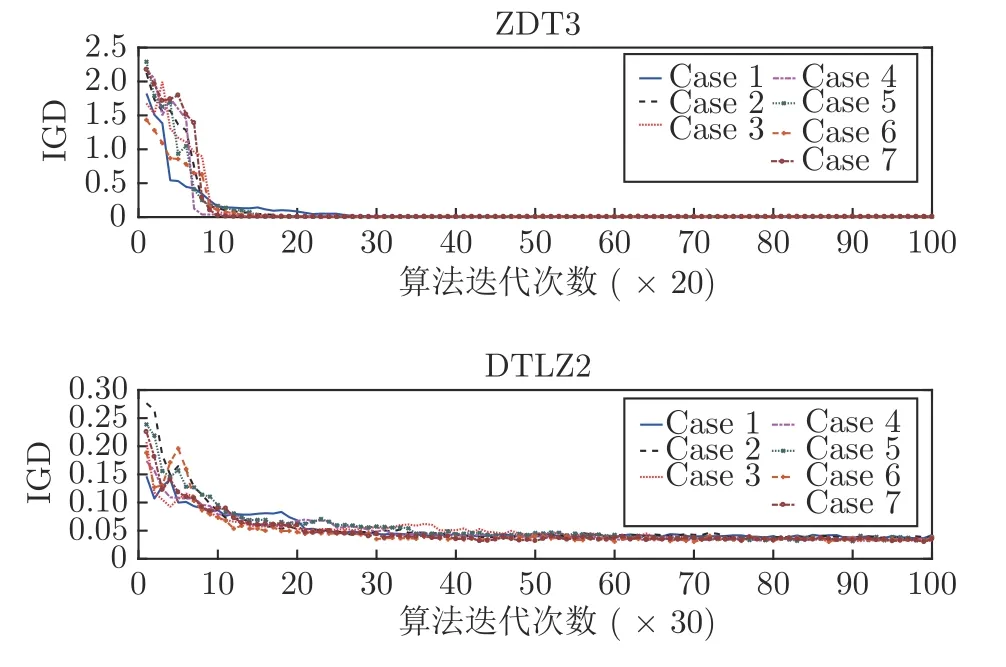
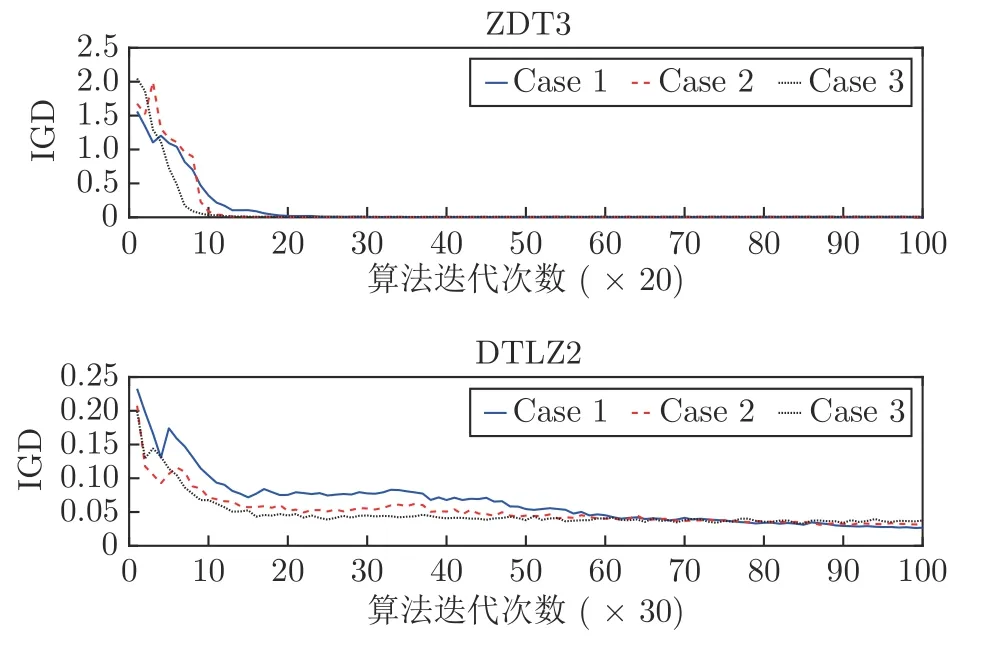
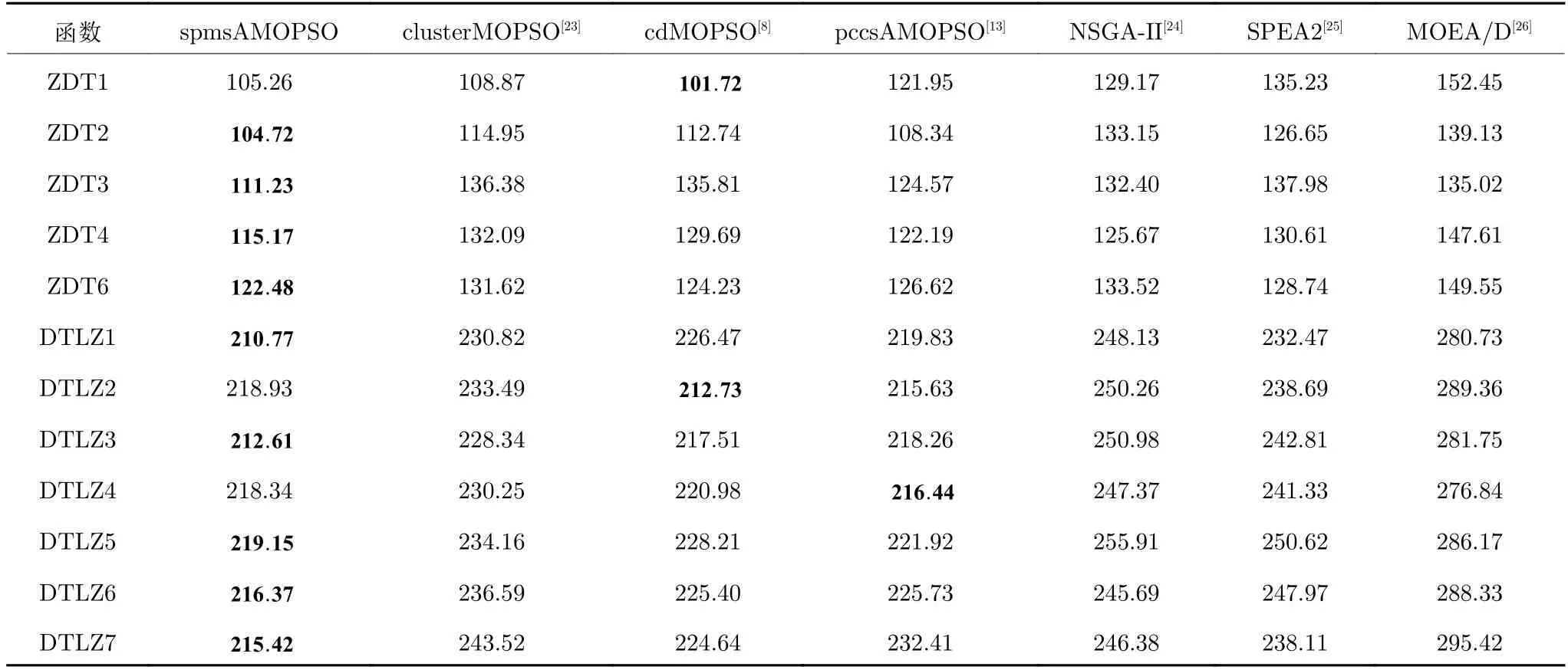
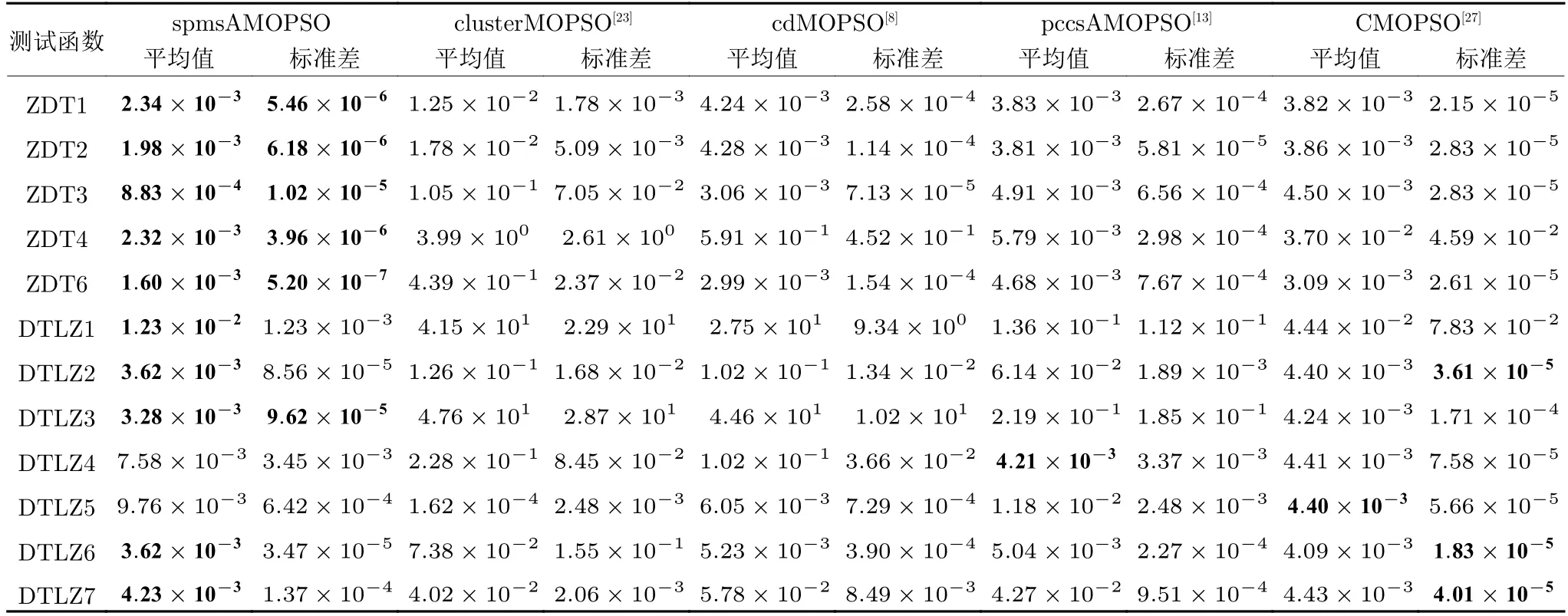
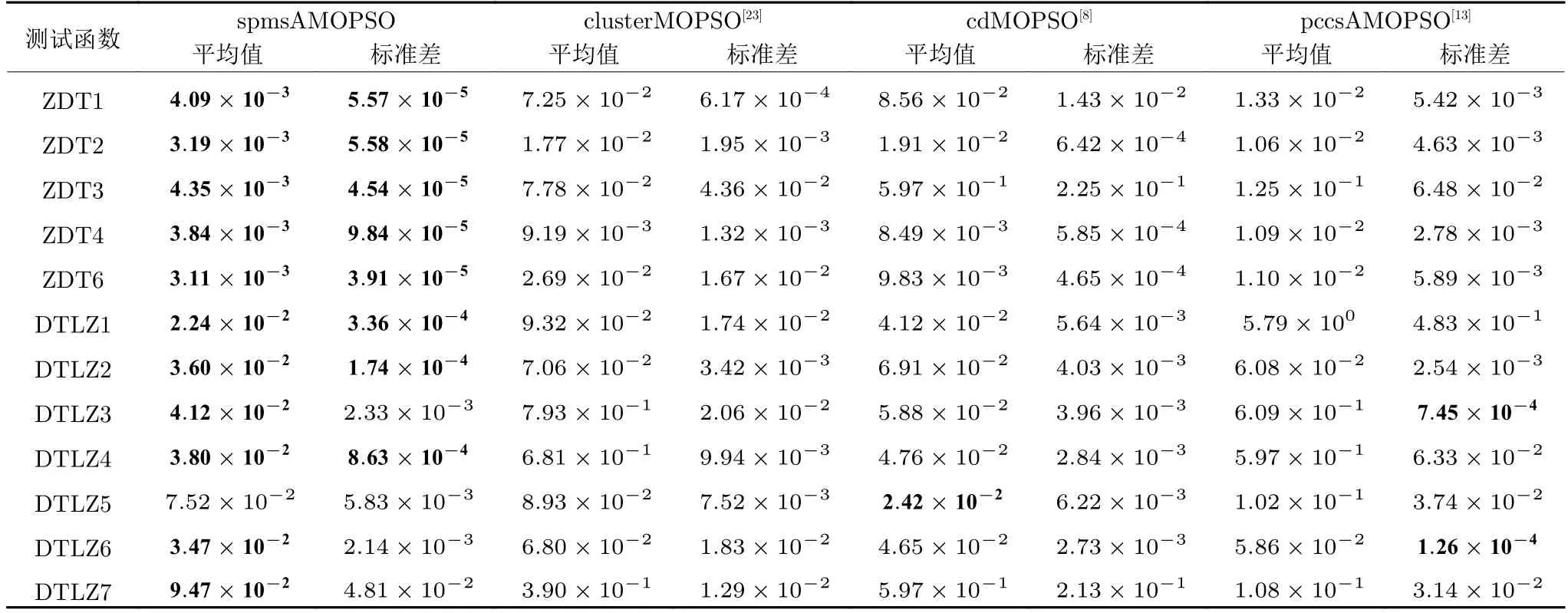
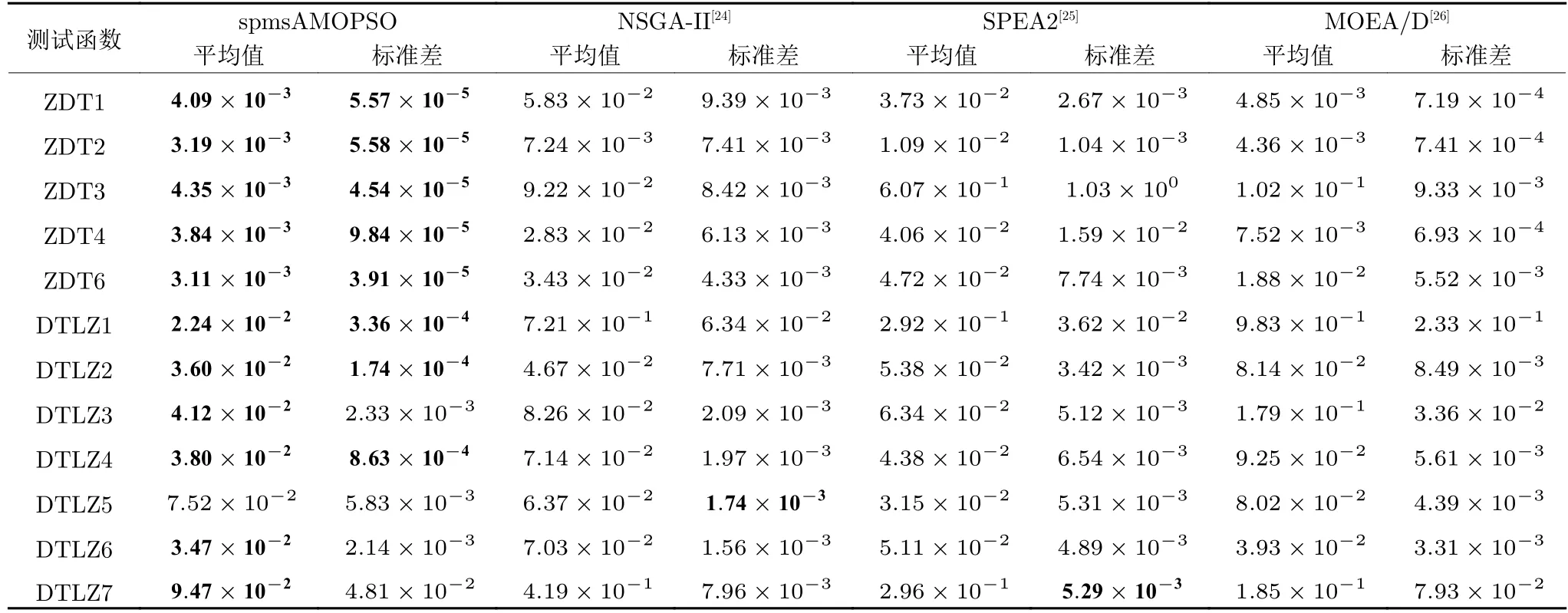
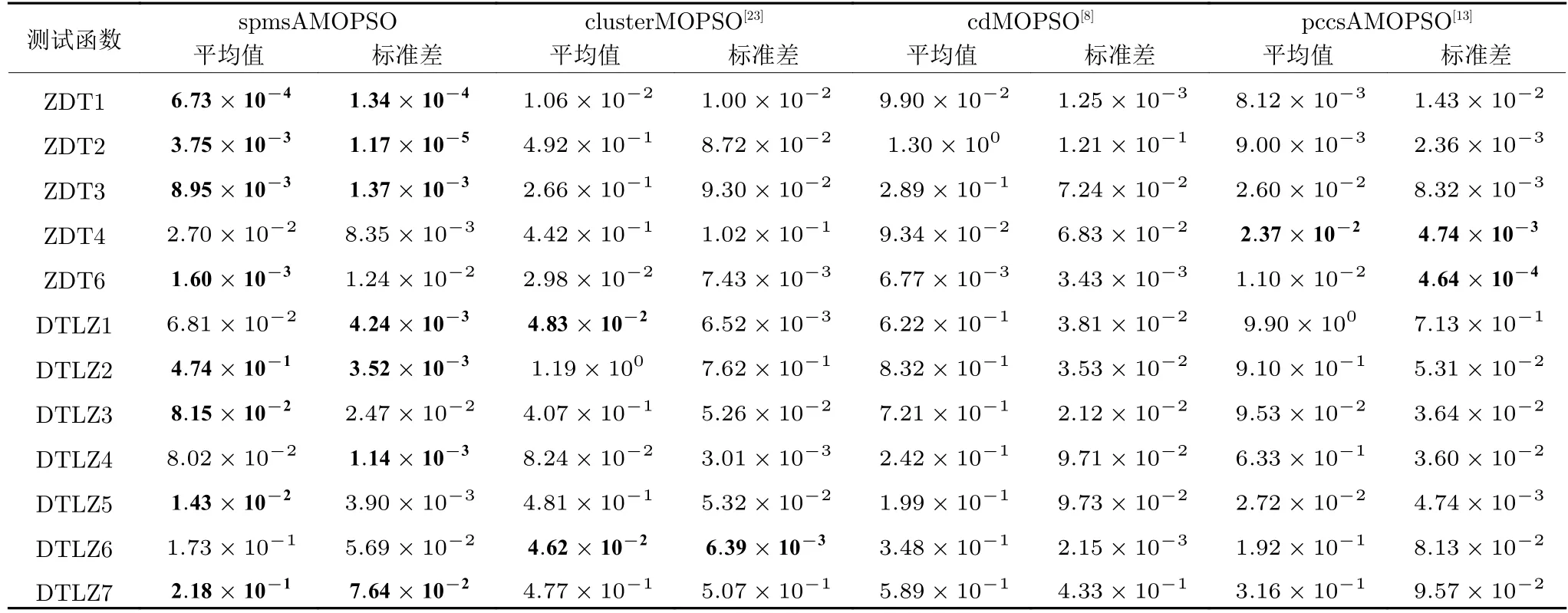
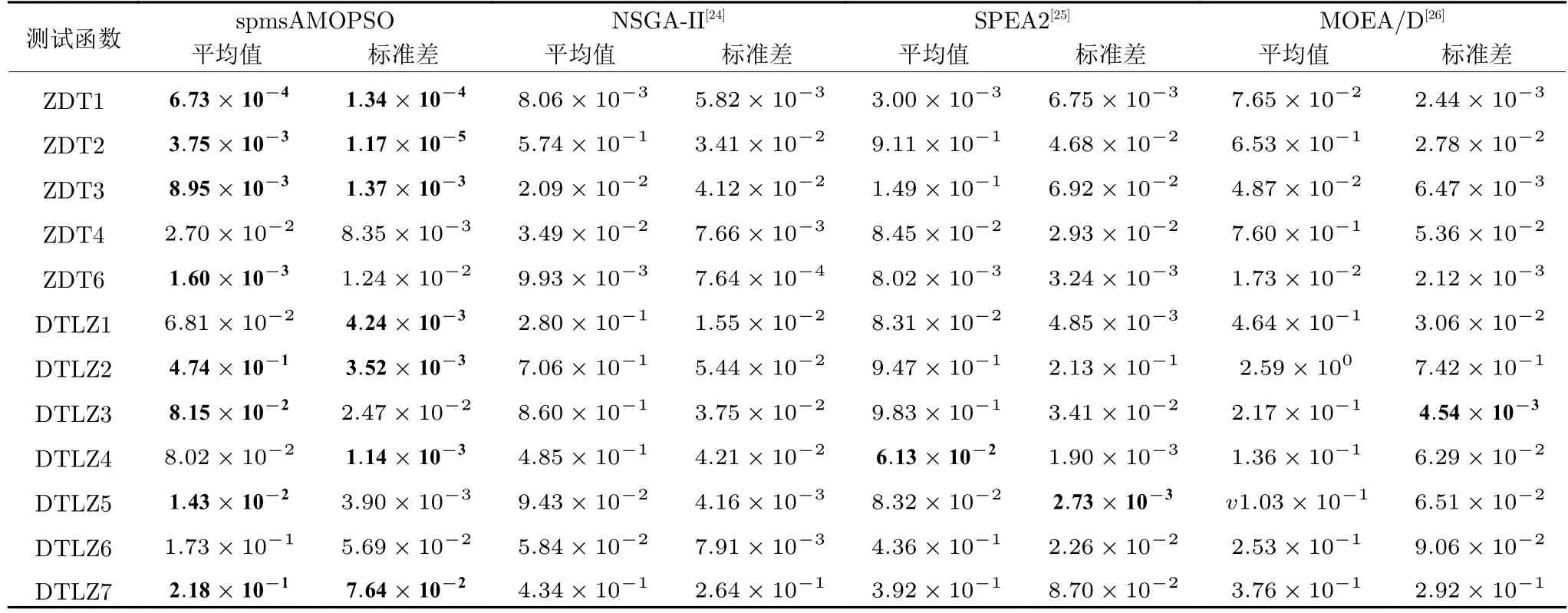
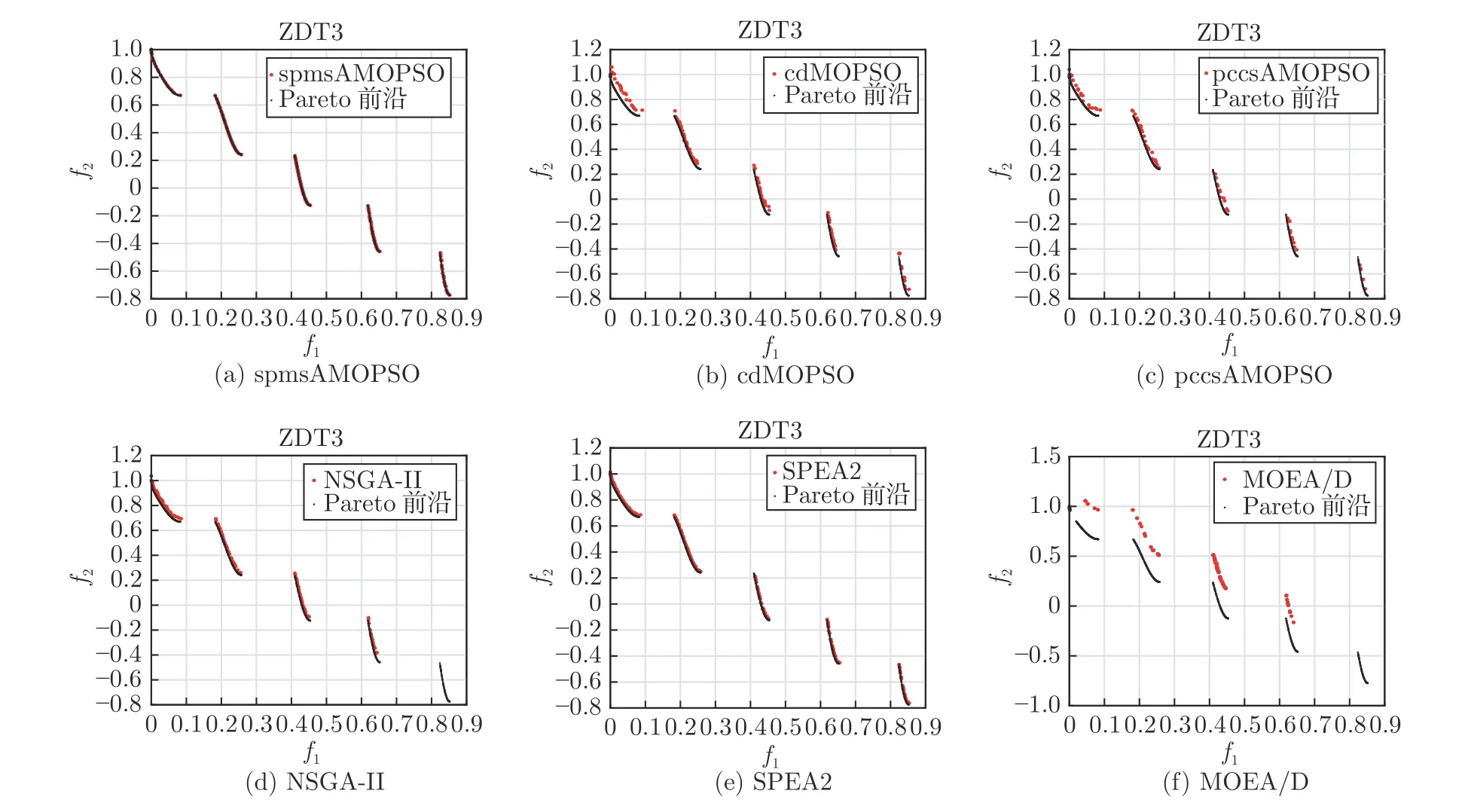
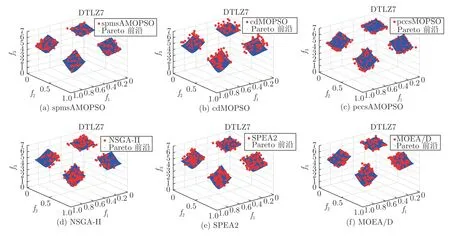
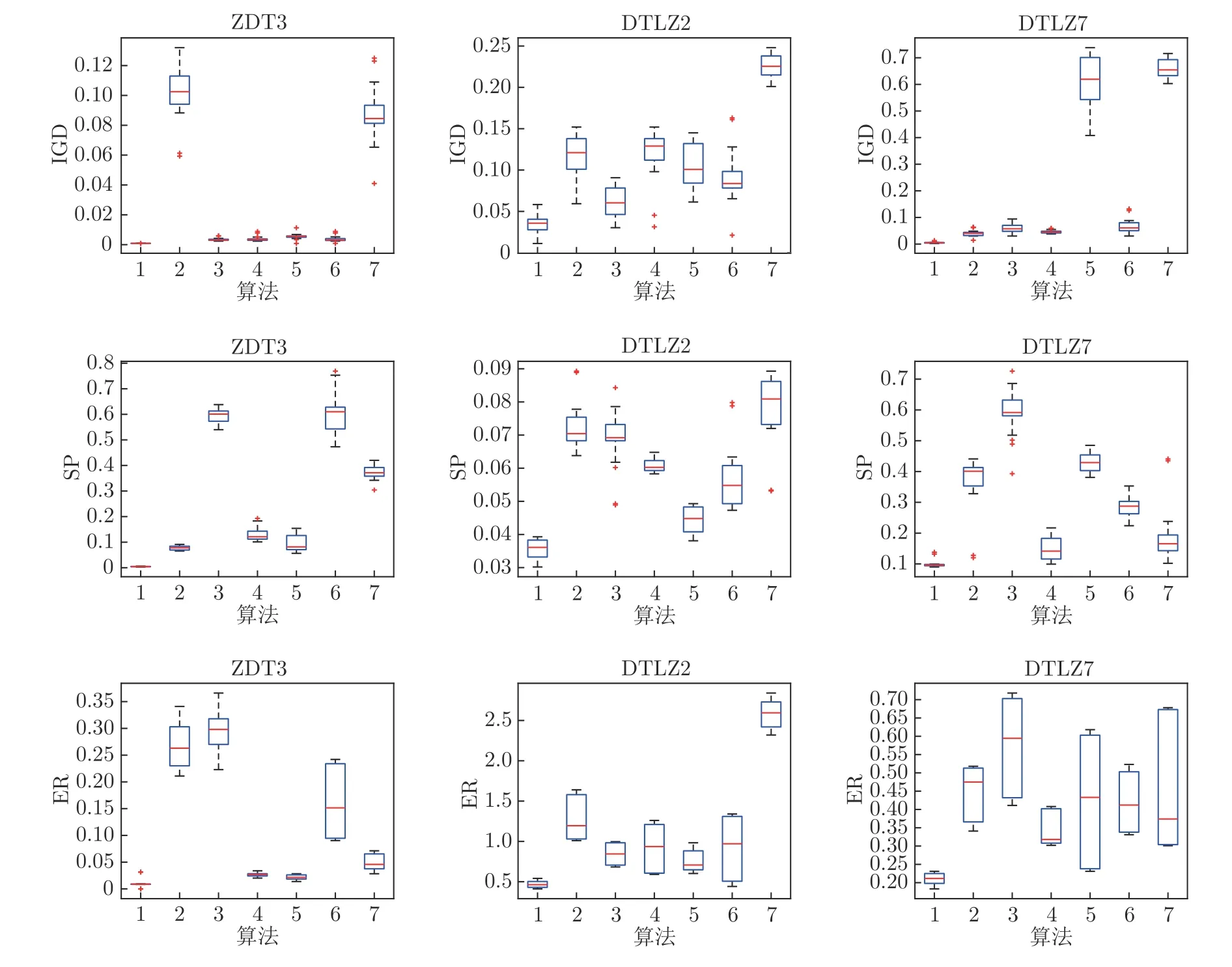
2) 若粒子i位于II 区,则其具有较好的性能,可以通过较少的迭代次数飞行至真实Pareto 前沿附近;若δ 3)若粒子i位于III 区,则粒子性能较差,距离真实Pareto 前沿较远,优先考虑增强粒子的收敛性;若δ <(1−pm),将粒子i向c-gbest方向进行变异: 式中,δ为区间[0,1]之间的随机数;d为区间[1,D] 之间的随机整数,D为问题的决策空间维数;xmax,d和xmin,d分别为d维决策空间上的最大值和最小值;pm为粒子变异因子,取值为pm=0.25+(t/2T);σ为高斯函数方差,根据算法迭代次数更新:σ=exp(−(t/T)); 方差σ控制变异范围,随迭代次数增加,使粒子的变异范围越来越小,保证算法迭代后期粒子的开发能力. 上述变异方法具有以下2 个优点: 1)算法能够根据粒子位置进行不同程度的变异,使算法跳出局部最优的同时避免对粒子搜索产生太大干扰,保持算法搜索连贯性.2)根据不同区域粒子的性能差异,制定不同的变异策略,扩大粒子的搜索区域,增强粒子的探索和开发能力. 合理选择个体最优粒子(pbest)有助于提高种群对局部空间的开发能力.多数MOPSO 算法均采用一个外部库来存储粒子的pbest,当粒子位置xi受pbesti支配时,pbesti保持,当xi支配pbesti时,将pbesti更新为粒子当前位置xi,两者无支配关系时,采用随机方法进行选取.这种方法虽然计算简单,但当xi与pbesti无支配关系时,选取的pbest不能有效指导粒子的飞行方向,易导致算法停滞[20]. 基于上述问题,本文提出一种带有记忆区间的pbest选取方法,在算法迭代过程中,每个粒子具有一个外部存储库,存储粒子最近几次迭代所经过的位置,形成记忆区间: 根据第2.2.1 节中粒子的融合排序方法,计算记忆区间中各位置的FR 指标,选取FR 指标最小的位置作为粒子i下一次迭代时的pbest: 当记忆区间饱和时,需要制定策略对记忆区间进行维护,图3 以2 个粒子为例,给出了粒子的记忆区间更新过程. 图3 粒子记忆区间更新过程Fig.3 Update process of particle memory interval 由图3 可以看出,粒子记忆区间更新存在两种情况:1)若存储位置达到记忆区间最大值,则将记忆中最早一次迭代时的位置遗忘,即.2)若为最优的粒子位置,则按时间顺序向后,将相邻的一个位置遗忘.即: 算法在迭代过程中将非支配解存入外部存档中,随着算法迭代次数增加,非支配解个数随之增加,当达到外部存档的最大容量时,需要对外部存档进行维护.多数MOPSO 算法在进行外部存档维护时,采用粒子的分布性能指标作为判断粒子性能的标准,将密度最大的粒子进行删除.这种方法虽然能够保持外部档案中非支配解的多样性,但可能会删除外部存档中收敛性较好的非支配解,导致种群产生退化,影响粒子开发能力[21].因此,在进行外部存档维护时不应将粒子密度作为外部存档维护的唯一性能指标,还应考虑到粒子的收敛性. 根据粒子的收敛性指标FR和粒子的分布性指标LD,采用融合的评价指标判断外部存档中粒子的综合性能: 由式(12)和式(14)可知,粒子FR 指标越小,粒子收敛性越好,LD 指标越大,粒子分布性越好.由式(26) 可以看出,粒子的综合排序(Comprehensive ranking,CR)指标不仅能够反映粒子的收敛程度而且包含了粒子的分布情况,粒子的CR 指标越小,表明粒子的综合性能越好.因此,当算法搜索到的非支配解个数超过外部存档的最大容量时,将外部存档中CR 指标较大的粒子删除. 为有效评价算法的收敛性和多样性,本文采用反世代距离(Inverted generational distance,IGD)、间隔指标(Spacing,SP)、出错比率(Error ratio,ER)和计算时间,分别对算法性能进行评价. 1) IGD: IGD 是度量真实Pareto 前沿与算法获得的近似Pareto 前沿之间的距离指标[13].IGD 值越小,表明算法获得的近似Pareto 前沿的收敛性和多样性越好,越接近真实Pareto 前沿,其计算方法为: 式中,PF为多目标算法所求得的Pareto 前沿;PF∗为真实Pareto 前沿的一组采样点;n为Pareto 前沿中非支配解个数. 2) SP: 用于度量每个解到其他解最小距离的标准差,是衡量一个范围内邻近解差异的重要指标[22].SP 值越小,表明解集分布越均匀,其计算方法为: 式中,di为第i个非支配解与其他解之间最小的欧氏距离;为所有di的平均值. 3) ER: 用来说明最优解的百分比[7].ER 越小,所得非支配解在真实Pareto 前沿中占比越高,其计算方法为: 式中,ei取值方法为: 若第i个非支配解在真实Pareto前沿中,则ei=0,否则ei=1. 4)计算时间t: 计算时间是多目标优化算法的重要性能评价指标之一[23],相同实验平台下算法的计算时间能够表征各算法的计算复杂度. 本节通过本文算法在不同参数取值方案下对ZDT3和DTLZ2 测试函数的实验,说明参数的取值方法.实验基本参数设置:种群粒子数量为100,外部存档最大容量为200,粒子记忆区间长度为u=5,粒子拥挤距离中S=4,变异策略中高斯函数的方差初始值σ0=0.8. 3.2.1 融合收敛性指标 FR 的权重 η1和η2 由式(14)所描述的融合收敛性指标FR的权重η1和η2的取值对粒子的收敛性评价产生影响,进而影响算法性能,合适的η1和η2取值能够有效对粒子进行分区,提升算法开发能力.本节通过多种参数取值下的实验,说明η1和η2的取值原因.选取7种参数取值方案: 分别对两目标问题ZDT3和三目标问题DTLZ2进行实验,测试ZDT3 问题时,每20 次迭代进行一次IGD 指标评价,测试DTLZ2问题时,每30 次迭代进行一次IGD 指标评价,实验结果如图4 所示. 图4 η1和η2 的不同取值方案下IGD 指标变化Fig.4 IGD metric changes of differentη1 and η2 value schemes 由图4 可以看出,在7种参数取值方案中,算法在Case 3~Case 5 的取值方案下,性能较好,即η1和η2的取值大小接近时,算法能够获得良好的性能.这是由于粒子平均排名AR和粒子全局损害GD 的计算方法造成的.粒子收敛性融合指标FR由AR和GD 的加权和构成,种群中粒子个数为100 时,粒子的AR 指标略大于GD 指标,当η1的取值远大于η2时,GD指标在粒子收敛性评价中几乎被忽略,即FR ≈AR.粒子的收敛性评价将由AR 主导,导致粒子收敛性评价不全面,算法性能下降,反之亦然.为保证本文算法性能,本文中η1和η2的取值分别为0.4和0.6. 3.2.2 分区参数 α 和β 第2.2.2 节通过分区参数α和β将种群划分为3 个区域,I 区和III 区最优粒子的选取可以保证算法基本的收敛性和多样性,II 区粒子能够根据算法当前环境进行自适应最优粒子的选取,提升粒子的探索和开发能力.因此,α和β的取值将影响算法的收敛速度和综合性能.图5 给出本文算法解决ZDT3和DTLZ2 问题时,3种α和β取值方案下IGD 指标下降趋势,取值方案分别为: Case 1:α=0.1N,β=0.9N;Case 2:α=0.2N,β=0.8N;Case 3:α=0.3N,β=0.7N.式中N为粒子总个数. 由图5 可以看出,当α和β的取值使II 区粒子数量较多时,算法收敛速度较慢,当II 区粒子数量较少时算法收敛速度较快.由ZDT3 测试问题的Case 3 可以看出,当II 区粒子数量较少时,算法的IGD 指标下降陡峭,并且算法迭代过程中IGD 指标下降无明显波动,表明算法在搜索过程中由于II区粒子数量不足,导致粒子的探索能力不足;由DTLZ2 测试问题可以看出,随着II 区粒子的增多,算法获得的最终IGD 指标逐渐减小,算法的综合性能逐渐提升. 图5 不同分区参数取值方案下IGD 指标变化Fig.5 IGD metric changes of different partition parameter value schemes 为避免算法收敛速度过快,保证种群中粒子的探索和开发能力,应使II 区粒子保持较高数量.通过大量实验验证,α和β的取值使I 区、II 区和III区粒子数分别约为粒子总数的1/5、3/5和1/5,能够使算法保持合适的收敛速度并获得良好的综合性能. 为验证本文算法的有效性,分别对两目标问题(ZDT 系列函数)和三目标问题(DTLZ 系列函数)进行实验测试,并设置8种多目标算法进行对比实验,对比算法包括: 基于聚类的多目标粒子群优化算法(MOPSO based on clustering,clusterMOPSO)[23]、cdMOPSO[8]、pccsAMOPSO[13]、非支配排序遗传算法(Nondominated sorting genetic algorithm II,NSGA-II)[24]、增强Pareto 进化算法(Strength Pareto evolutionary algorithm,SPEA2)[25]、MOEA/D[26]、基于竞争机制的多目标粒子群优化算法(Competitive mechanism based MOPSO,CMOPSO)[27]和嵌入基于分解归档方法的SPEA2 算法(Decomposition-based archiving approach embedded in SPEA2,SPEA2+DAA)[28]算法.各算法对测试问题的最大评价次数均为1 000 次,实验结果均为各算法在同一测试问题上独立运行30 次的统计结果.算法运行环境均为Inter Core i5-5257U 2.70 GHz CPU,8 GB 内存,Windows10 操作系统,Matlab 2016b.各对比算法参数设置均与原文献保持一致. 表1~6 分别给出了包括本文spmsAMOPSO 算法在内的多种多目标优化算法在12 个测试问题上的IGD、SP 以及ER 性能指标的平均值和标准差.表7 给出了几种算法计算所需的时间,其中粗体数据为各评价指标下所得的最优结果. 表7 不同算法对多目标测试问题的运行时间 (s)Table 7 Computational time of different algorithms for multi-objective test problems (s) 由表1~2 可以看出,本文算法在12 个测试问题的结果中,获得10 次IGD 指标的最优平均值和6 次标准差最优值.虽然在DTLZ4 测试问题中本文算法的IGD 指标略逊于pccsAMOPSO 算法(其结果为最优值,本文算法结果为次优值),但优于其中5种多目标算法.这是由于本文算法在进行最优粒子选取时采用分区策略,将部分性能相似的粒子划分为一个区域,对一个区域的粒子实现一种搜索引导策略,而pccsAMOPSO 算法在进行全局最优粒子选取时,对种群中粒子逐个进行选取,而本文算法根据粒子当前性能进行分区所获得的分区较为模糊,在对复杂多目标问题进行优化时,综合性能表现稍显不足.但本文算法通过种群分区策略,提出一种新的变异方法,并结合带有记忆区间的个体最优粒子选取和融合指标的外部存档维护等方法,使本文算法最终仍具有良好的性能.在DTLZ5测试问题中本文算法性能相较于CMOPSO 算法和cdMOPSO 算法具有一些劣势(综合性能上CMOPSO 算法最优,cdMOPSO 算法次优),但优于其余6种多目标优化算法.对其余测试问题中,本文算法均取得IGD 指标的最优值,各算法在12个测试问题中的IGD 最优值个数表明,本文算法在综合性能上优于其他8种多目标优化算法. 表1 本文算法与其他多目标粒子群算法的IGD 评价指标对比Table 1 Results of IGD metric of the proposed algorithm and MOPSOs 表2 本文算法与其他多目标进化算法的IGD 评价指标对比Table 2 Results of IGD metric of the proposed algorithm and multi-objective genetic algorithms 由表3和表4 可以得到,本文算法在12 个测试问题的结果中,获得11 次SP 指标的最优平均值和7 次标准差最优值.在DTLZ5 测试问题中,本文算法的SP 指标略逊于cdMOPSO和NSGA-II 算法(cdMOPSO和NSGA-II 算法分别获得最优值和次优值),但优于pccsAMOPSO、clusterMOPSO、MOEA/D和SPEA2 等4种多目标优化算法,在其余测试问题中,本文算法的SP 指标均取得最优值.实验结果表明,相比于其余多目标优化算法,本文算法获得的Pareto 前沿中非支配解分布均匀,算法具有良好的多样性. 表3 本文算法与其他多目标粒子群算法的SP 评价指标对比Table 3 Results of SP metric of the proposed algorithm and MOPSOs 表4 本文算法与其他多目标进化算法的SP 评价指标对比Table 4 Results of SP metric of the proposed algorithm and multi-objective genetic algorithms SP 指标的实验结果表明,本文算法获得的非支配解集具有良好的多样性,这是由于本文算法通过对算法环境的检查自适应地调整了算法惯性权重和学习因子,并采用种群分区策略,对种群中收敛性较好的粒子制定特殊的搜索引导策略和变异方法,提升粒子的探索效率,有效增强算法多样性. 由表5~6 可以看出,在12 个测试问题的结果中,本文算法共获得8 次ER 评价指标的最优值,在求解ZDT4、DTLZ1和DTLZ4 测试问题时取得次优值(MOEA/D、clusterMOPSO和SPEA2 算法分别取得最优值).在DTLZ6 测试问题中,本文算法的ER 指标略逊于clusterMOPSO和NSGAII 算法,这是由于本文算法在最优粒子选取,变异以及外部存档维护等方面均采用不同的策略对算法的收敛性和多样性进行平衡,即牺牲了粒子的部分局部开发能力换取粒子的全局开发能力,使算法取得相较于其他算法更好的多样性,因此在部分复杂多目标优化问题中收敛性略显不足.但相比于cdMOPSO 等其余4种多目标优化算法,本文算法在收敛性上仍然具有一定优势.综合各算法的ER 评价指标实验结果,本文spmsAMOPSO 算法获得的非支配解集能够较好地逼近真实Pareto 前沿,相比于其他几种多目标优化算法,具有良好的收敛性. 表5 本文算法与其他多目标粒子群算法的ER 评价指标对比Table 5 Results of ER metric of the proposed algorithm and MOPSOs 表6 本文算法与其他多目标进化算法的ER 评价指标对比Table 6 Results of ER metric of the proposed algorithm and multi-objective genetic algorithms ER 指标的实验结果表明,本文算法相较于其他几种多目标优化算法具有更好的收敛性,这是由于本文算法通过在最优粒子选取和变异中加入种群分区,对种群中性能较差的粒子实行特殊的寻优策略,增强劣势粒子的利用率,有效提升算法收敛性;在个体最优粒子选取中,加入粒子的记忆机制,提升个体最优粒子选取的可靠性,增强个体最优粒子对粒子收敛过程的指导作用. 由表7 可以看出,本文算法在求解多数测试问题时具均有较好的实时性,仅在ZDT1和DTLZ2问题时劣于cdMOPSO 算法,在DTLZ4 问题时略逊于pccsAMOPSO.虽然本文算法采用了分区机制和粒子记忆区间,增加了算法的计算复杂度,但有效的种群划分使粒子的全局最优粒子选取以及变异更有效率,并且个体最优粒子的可靠选取使粒子能够更快收敛至Pareto 前沿附近,使算法运行时间相较其他同类型优化算法更短. 为详细说明各算法所得非支配解集的收敛性和多样性,图6~8 分别给出了6种算法在求解ZDT3、DTLZ2和DTLZ7 测试问题时的非支配解集和真实Pareto 前沿.由实验结果可以看出,在三种测试问题中,cdMOPSO、pccsAMOPSO、NSGA-II、SPEA2和MOEA/D 等多目标优化算法均不同程度的出现了收敛性和多样性不足的问题.同样是在DTLZ2 测试问题中,cdMOPSO、NSGA-II和SPEA2 算法均表现出收敛性不足的缺点,虽然pccs-AMOPSO和MOEA/D 算法具有较好的收敛性,但算法多样性较差,而本文spmsAMOPSO 算法得到的Pareto 前沿中,非支配解不仅较好地收敛在真实Pareto 前沿附近,而且具有良好的分布性,算法在收敛性和多样性上均有较好表现. 图6 不同多目标优化算法对ZDT3 函数的Pareto 前沿Fig.6 Pareto front of ZDT3 function of different multi-objective optimization algorithms 图8 不同多目标优化算法对DTLZ7 函数的Pareto 前沿Fig.8 Pareto front of DTLZ7 function of different multi-objective optimization algorithms 为直观展示各算法多次实验数据的分布情况,图9 分别给出了7种多目标优化算法在测试ZDT3、DTLZ2和DTLZ7 问题时IGD、SP 以及ER 指标的箱形图,其中横轴坐标1~7 分别代表spmsAMOPSO、clusterMOPSO、cdMOPSO、pccsAMOPSO、NSGA-II、SPEA2和MOEA/D 算法.由图9可以看出,本文算法在求解ZDT3、DTLZ2和DTLZ7测试问题时,IGD、SP 以及ER 指标相较于其他6种多目标优化算法均具有较大优势,并且本文算法的多次测试结果数据无明显偏态,出现的异常数据较少,各项性能指标的中值和最大偏差均优于其他多目标优化算法.实验结果表明,本文算法不仅具有良好的综合性能,并且测试结果稳定. 图9 7种多目标优化算法在测试ZDT3、DTLZ2和DTLZ7 问题时IGD、SP 以及ER 指标的箱形图Fig.9 Box plots of IGD,SP and ER metric on ZDT3,DTLZ2 and DTLZ7 problems of multi-objective optimization algorithms 综合实验结果表明,本文算法得到的非支配解集能够有效地收敛在真实Pareto 前沿,并具有良好的分布性.这是由于本文算法通过对种群进行分区,制定多策略的搜索引导方案,有效平衡了算法的收敛性和多样性,提升了粒子的探索和开发能力及寻优效率,并且使算法具有较好综合性能的同时降低了算法的计算复杂度. 本文提出了一种基于种群分区的多策略自适应多目标粒子群优化算法.算法通过基于种群分区的多策略改进,确定算法的全局最优粒子选取和变异方法,将粒子性能与算法寻优过程结合,提升种群中各个粒子的搜索效率;提出带有记忆区间的个体最优粒子选取方法,提升个体最优粒子选取的可靠性,避免因个体最优粒子不能有效指导粒子的飞行,使算法停滞,陷入局部最优;采用双性能测度指标的外部存档维护策略,能够有效保持外部存档中非支配解良好的分布性,避免进行外部存档维护时,删除收敛性较好的粒子,导致种群产生退化,影响粒子开发能力.为验证算法有效性,采用ZDT和DTLZ系列测试函数进行仿真实验,并与其他几种多目标优化算法进行对比,通过各算法对同一测试问题的IGD、SP、ER 以及计算时间等评价指标的实验结果,分别说明本文算法的收敛性,多样性和实时性.综合实验结果表明,本文算法具有较显著的收敛性和多样性优势,且具有良好的实时性.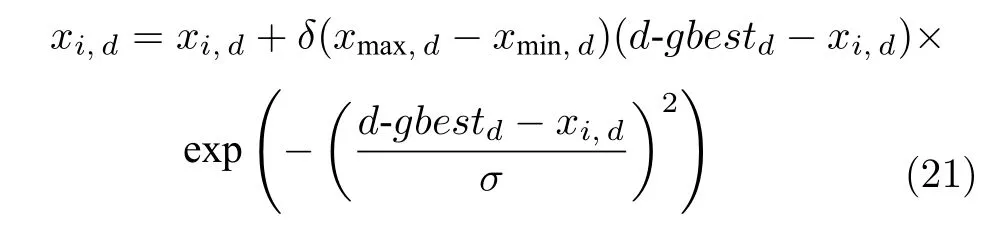
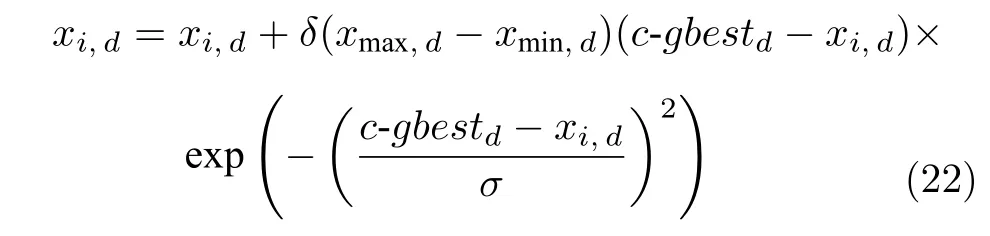
2.4 带有记忆区间的个体最优粒子选取方法
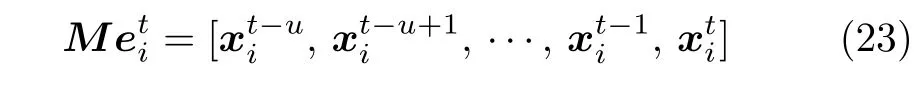
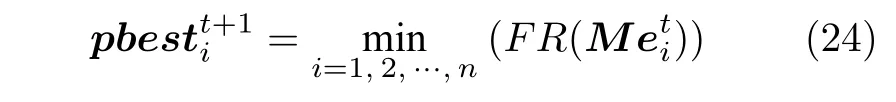
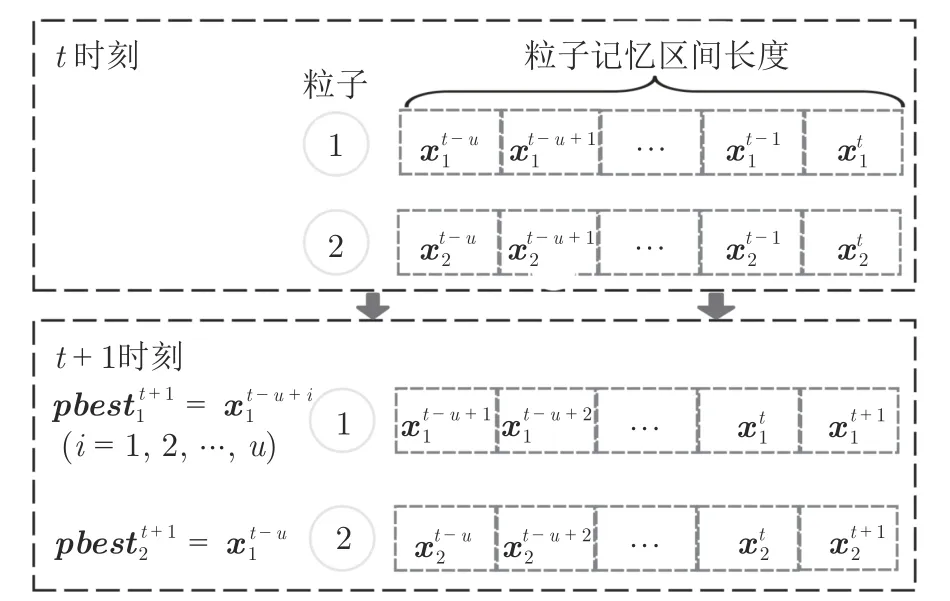
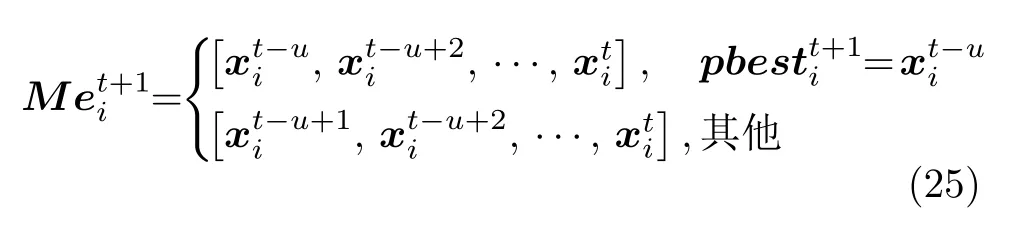
2.5 基于双性能测度融合指标的外部存档维护
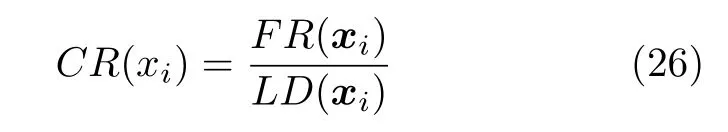
3 实验分析
3.1 性能评价指标
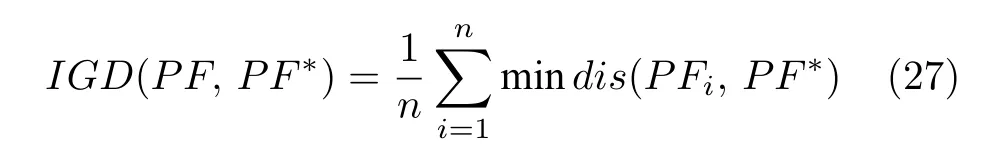
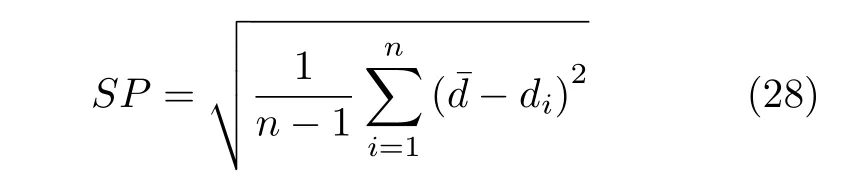
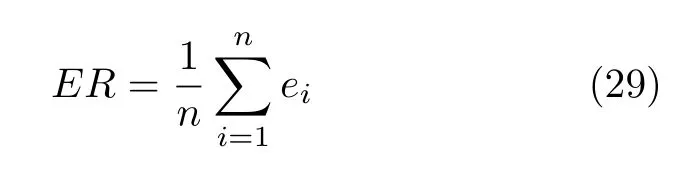
3.2 参数取值和分析
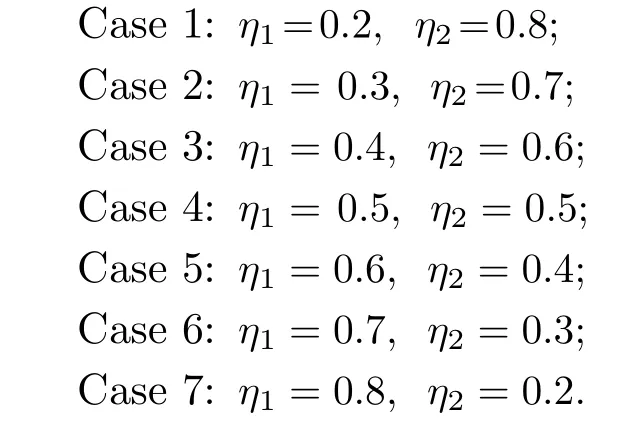
3.3 实验结果及比较分析

4 结束语

