液环泵轴向叶顶间隙泄漏流动的等离子体控制数值研究

郭广强 王静宜 张人会 陈学炳 杨军虎

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.兰州理工大学甘肃省流体机械及系统重点实验室， 兰州 730050)

0 引言

液环泵是以液体作为能量转化的中间介质，用来抽送气体的流体机械[1],由于其在抽送气体过程中具有近似等温压缩及无转子金属表面接触等优点，在抽送易燃易爆、有毒害及可凝性气体时具有极大优势，广泛应用于石化、电力及煤矿等领域；但是液环泵内复杂的气液流动导致其效率低及振动噪声大，其中叶轮轴向间隙泄漏流动是造成泵内复杂流动的主要原因之一。在液环泵内叶片工作面与背面、排气区与吸气区之间的压差作用下，介质在叶轮轴向端面间隙处产生泄漏高速射流，其与流道内的主流剪切、卷吸及掺混形成剪切涡及泄漏涡等复杂流动结构[2-3]，导致泵内的水力损失增大、水力激励特性复杂，进而限制泵的高效稳定运行[4-5]。

目前国内外学者在液环泵内复杂气液两相流动及轴向间隙泄漏流动控制方面做了较多的研究[6-11]。虽然现有的研究对液环泵轴向间隙泄漏流动控制进行了报道，但主要集中在被动流动控制方面，尽管被动流动控制在设计工况下会取得较好的效果，但其对工况变化的自适应能力差，且在非设计工况下会产生额外的附加阻力[12]。

等离子体气动激励是近年来兴起的一种新型主动流动控制技术，具有功耗低、无运动部件、激励频带宽及易于大面积铺设等优点[13]，受到了国内外研究者的广泛关注。目前在压气机失速及扩稳的等离子体流动控制等方面学者们开展了大量的研究[14-18]。

本文将等离子体激励引入水力机械内流动控制，提出基于介质阻挡放电等离子体激励的液环泵叶轮轴向叶顶间隙泄漏流动控制方法，耦合唯象学模型、RNGk-ε湍流模型及流体体积法(Volume of fluid, VOF)气液两相流模型对等离子体激励下的液环泵轴向叶顶间隙泄漏流场进行数值模拟，分析等离子体激励调控液环泵轴向间隙泄漏流动的机理及不同激励电压对泄漏流动的控制效果。

1 研究模型与计算方法

1.1 研究模型及其网格划分

以2BEA型液环泵为研究模型，为了实现泵内气液流动结构的可视化，将原型双吸式泵的结构进行改造，其传动端被改造为吸、排气端，非传动端为透明材质制作的可视化视窗，如图1所示。模型泵的基本参数：壳体半径R为212 mm，叶轮轴向宽度bw为130 mm，叶轮外圆半径r2为183 mm，叶轮轮毂半径r1为91 mm，叶轮轴向间隙宽度fd为0.5 mm，偏心距ed为23.1 mm，叶片数Z为18，转速n为1 450 r/min。采用Pro/E软件对模型泵计算域进行几何建模，为了减少计算量，建模时忽略吸排气侧的轴向间隙，保留侧盖一侧的轴向间隙，其计算域包括叶轮、壳体、进口延伸段、出口延伸段及轴向间隙。采用ANSYS-ICEM软件对模型泵计算域进行六面体结构网格划分，如图2a所示，全流场计算网格总数约为6.50×106；图2b(图中PS表示叶片压力面，SS表示叶片吸力面)为s/c=0.20(s/c为叶片弦长系数，为叶片某一位置处的弦长占整个叶片弦长的比值)处垂直于叶片骨线截面P上的网格结构，为了能够精确捕捉叶轮轴向间隙泄漏流动结构，在间隙区域沿轴向布置18层网格，并对与间隙相邻计算域的网格进行局部加密，保证轴向间隙网格与相邻计算域网格的均匀过渡。

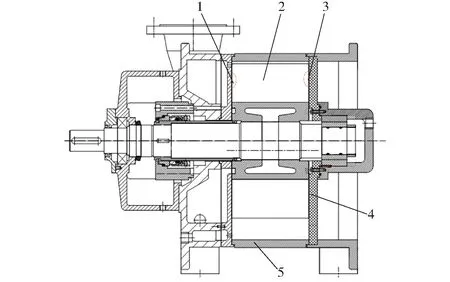
图1 研究模型结构图Fig.1 Structure diagram of research model1、3.轴向间隙 2.叶轮 4.侧盖 5.壳体

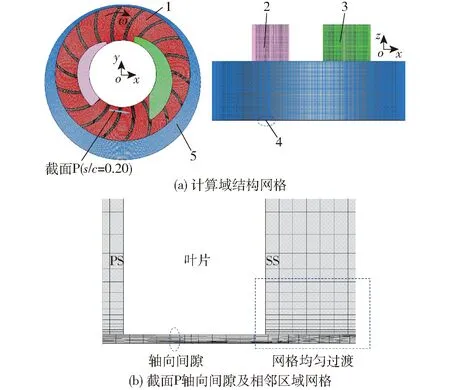
图2 计算网格Fig.2 Computational grid1.叶轮 2.排气段 3.吸气段 4.轴向间隙 5.壳体

1.2 计算模型及边界条件

选择VOF模型模拟液环泵内部气液两相流动，该模型中两种相互不相容的流体共用一套动量方程，并通过引入相体积分数来追踪计算域内的相界面[8]，模拟过程中将计算域内与泵壳同心的圆柱表面至壳体内表面区域设置为初始液相区域，液相设置为液态水，气相设置为可压缩性理想气体；考虑重力及相界面表面张力对流场的影响。湍流模型采用RNGk-ε模型；采用滑移网格处理转子与静子之间的相互作用；进口边界条件设置为质量流量进口，出口设置为压力出口，参考压力为101 325 Pa；非稳态计算时间步长设置为9×10-6s，数值模拟过程中，监测液环泵的进口真空度，当其周期性稳定脉动时，计算收敛。

本研究采用介质阻挡放电[13]等离子体激励方式对液环泵轴向间隙泄漏流动进行控制。等离子体激励与间隙泄漏流场耦合的数值模拟采用文献[19]提出的唯象学模型，其根据大量的力学研究及实验，提出将等离子体作用区域简化为一个三角形(OAB)区域，如图3所示；求解该区域的电场力，将电场力作为体积力源项加入到N-S方程中，对流场进行模拟。

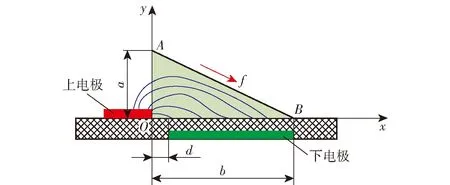
图3 等离子体激励的等效区域Fig.3 Equivalent region of plasma excitation

原点O处的电场强度E最大，电场强度在OAB区域内呈线性分布，可表示为

E(x,y)=E0-k1x-k2y

(1)

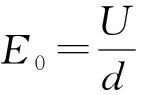
(2)

(3)

(4)

式中E0——原点处的电场强度，kV/cm

U——电极间施加的最大电压，kV

d——两电极在x方向的距离，mm

Eb——等离子体流动边界的击穿电场强度，kV/cm

x、y方向的电场强度分量可表示为

(5)

(6)

等离子体激励产生的体积力可由电场力表示，该区域电场力的方向平行于AB边并指向斜下方，因此x、y方向的体积力可表示为

fx=ρceExγ1Δt

(7)

fy=ρceEyγ1Δt

(8)

式中ρc——等离子体密度，cm-3

e——元电荷，C

γ1——激励频率，kHz

Δt——一个激励周期等离子体作用时间，μs

根据等离子体激励的位置参数、激励电参数及电荷密度等求解体积力fi，通过编写UDF(User defined functions)程序将其作为体积力源项加入到动量方程中，并添加到液环泵端盖内壁等离子体激励的流动控制区域，对等离子体激励下的泵内轴向间隙泄漏流场进行数值模拟。

由于液环泵排、吸气区之间压差的作用，导致吸气口末端至排气口始端气相区域泄漏较为严重；因此，在该区域的泵侧盖内壁均匀布置9组等离子体激励器，如图4所示。等离子体激励布局中，激励器沿径向布置，预期可产生一个与泄漏流流向相反的体积力分量来对间隙泄漏流动进行干扰(图4)，以实现对泄漏流动的调控。本研究中a=0.5 mm、b=5 mm、d=0.25 mm，激励频率γ1=20 kHz，等离子体作用时间Δt=67 μs，等离子体密度ρc=1011cm-3，激励电压分别设置为10、15 kV，击穿电场强度为30 kV/cm。

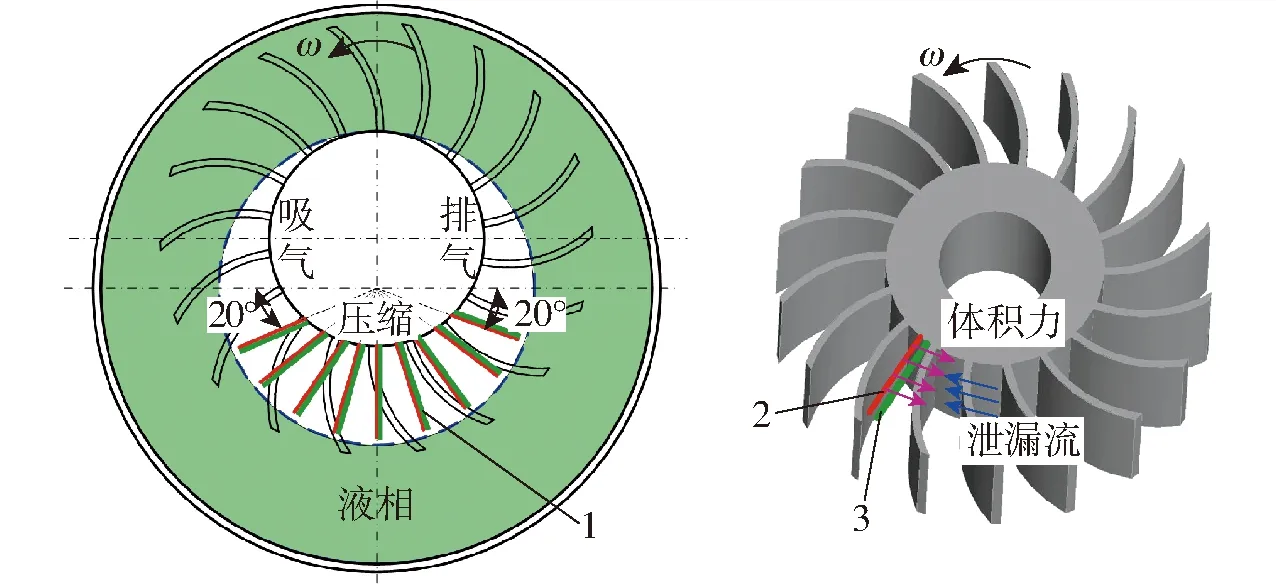
图4 液环泵轴向端壁等离子体激励布局Fig.4 Layout of plasma excitation on axial end wall of liquid ring pump1.等离子体激励器 2.上电极 3.下电极

2 结果与分析

2.1 计算方法验证

针对本文采用的液环泵研究模型，课题组前期已开展了泵内气液流动结构可视化及水力性能的实验研究，具体实验装置及测试方法详见文献[20]，相关实验数据可用于本研究数值模拟的准确性验证；液环泵的效率[6]计算公式为

(9)

式中p1——泵进口绝对压力，Pa

p2——泵出口绝对压力，Pa

qv——泵吸气体积流量，m3/s

M——作用于叶轮的扭矩，N·m

ω——叶轮角速度，rad/s

图5为无施加等离子体激励的液环泵水力性能的数值与实验结果对比图，由图5可以看出，由于数值计算的泵进口真空度大于实验结果，图中数值得到的泵吸气压力小于实验结果，效率η高于实验结果；数值计算的泵进口压力及效率随流量的变化趋势与实验结果一致，其值随流量的增大呈逐渐增大的趋势，但是数值与实验结果之间存在一定的误差，其主要原因是在数值计算时忽略了泵传动端一侧的轴向间隙泄漏流动损失及数值模拟网格难以捕捉液环泵内的微小尺度气液湍流结构。

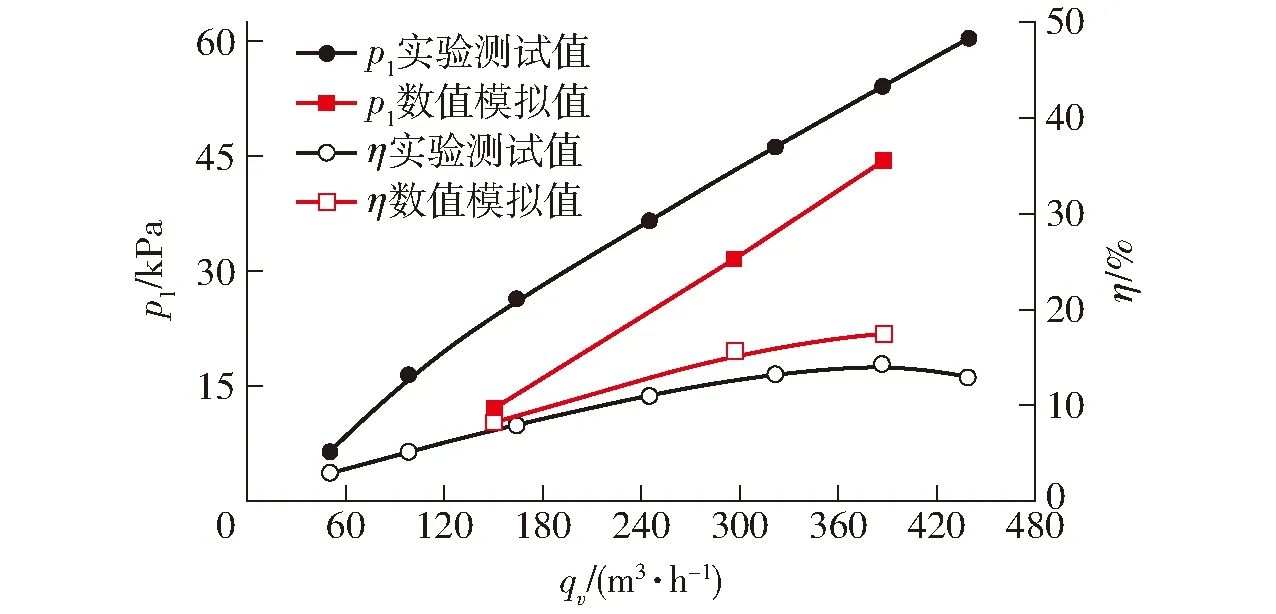
图5 水力性能数值模拟与实验结果对比Fig.5 Comparison between numerical simulation and experimental results of hydraulic performance

图6为不施加等离子体激励下液环泵叶轮轴向中间截面相态场分布的数值及实验结果对比，由图6可以看出，数值模拟得到的气液自由分界面形状与可视化结果基本一致，均表现为与泵壳体同心的近似圆形且液环内表面为锯齿不连续状。为了进一步验证数值模拟结果的准确性，对如图6所示的泵内1/4圆周液环内表面的大小进行分析；在数值及实验结果的1/4圆周内，以间隔18°定义5个位置W1、W2、…、W5(图6)，对各位置处液环内表面的半径ri进行无量纲化处理，得到无量纲化系数k=ri/R。表1为各参考位置处液环内表面k数值模拟与实验结果对比，可以看出数值模拟结果ks与实验值ke间的相对误差ζ均在5%以内。上述表明采用的数值方法基本可以捕捉泵内的主要流动结构。笔者前期对液环泵内部流动数值模拟方法的研究[8]也印证了本文数值方法的可行性。

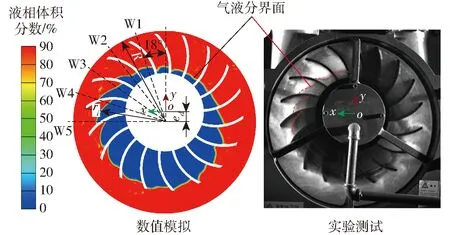
图6 泵内气液两相分布数值模拟与实验结果对比Fig.6 Comparison between numerical and experimental results of gas-liquid two-phase distribution in pump

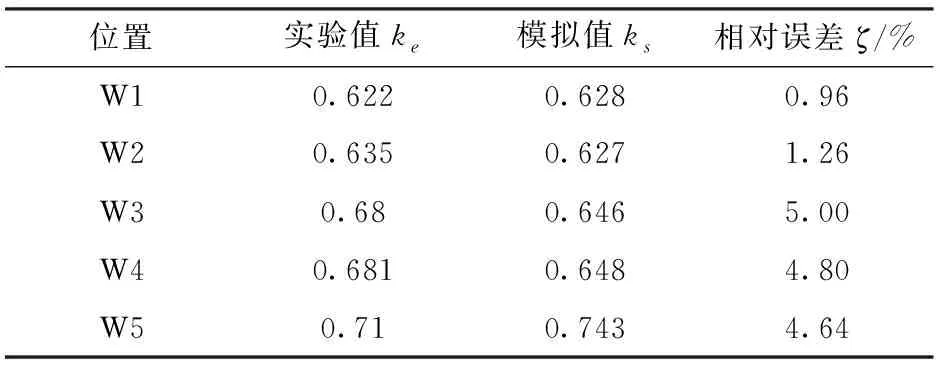
表1 泵内不同位置液环内表面k的数值与实验结果对比Tab.1 Comparison between numerical and experimental results of inner surface of liquid-ring at different positions in pump

2.2 轴向间隙泄漏流场分析

基于液环泵在吸气质量流量qm为0.03 kg/s工况下的数值模拟结果，选取泵内气液两相流动非稳态数值计算收敛后0.184 42 s时刻的计算结果，分析轴向间隙泄漏流结构及其等离子体流动控制机理。

为了分析液环泵轴向叶顶间隙泄漏流场结构及其等离子体激励的流动控制效果，在间隙的轴向中间位置截取截面A；在压缩区同一叶片上以不同s/c截取截面B、C，如图7所示。

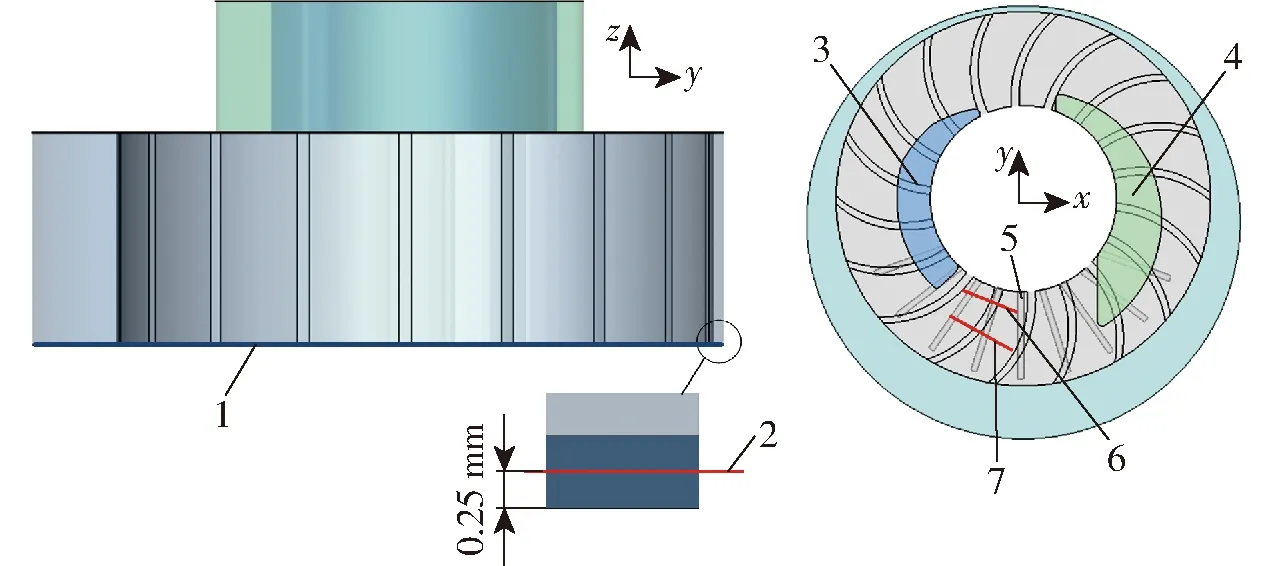
图7 截面位置示意图Fig.7 Schematic of section position1.轴向间隙 2.截面A 3.排气口 4.吸气口 5.等离子体激励区 6.截面B(s/c=0.20) 7.截面C(s/c=0.50)

图8为液环泵间隙轴向中间截面(截面A)的速度和截面C近壁区域的速度分布图。由截面A速度分布可以看出，排、吸气口之间的压差作用，导致排气区始端至吸气区末端区域出现明显的泄漏高速射流分布；由截面C近壁区域速度分布可以看出，泄漏高速射流沿旋转反方向流出间隙后，与叶轮主流相互作用并逐渐耗散。

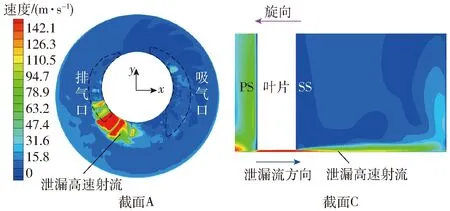
图8 截面A、C的速度分布Fig.8 Velocity distribution on section A and C

2.3 等离子体激励调控间隙泄漏流场分析

在液环泵内气液两相流动的非稳态数值模拟收敛后，按照图4所示的等离子体激励布局，由激励位置及激励电参数编写UDF程序，并将其加载到等离子体激励区域，开展等离子体激励与泄漏流场耦合的数值模拟。图9为激励电压为10 kV和15 kV下等离子体激励诱导的体积力分布图，可以看出，体积力在近似三角形区域内呈均匀变化趋势，靠近原点位置，体积力逐渐增大。

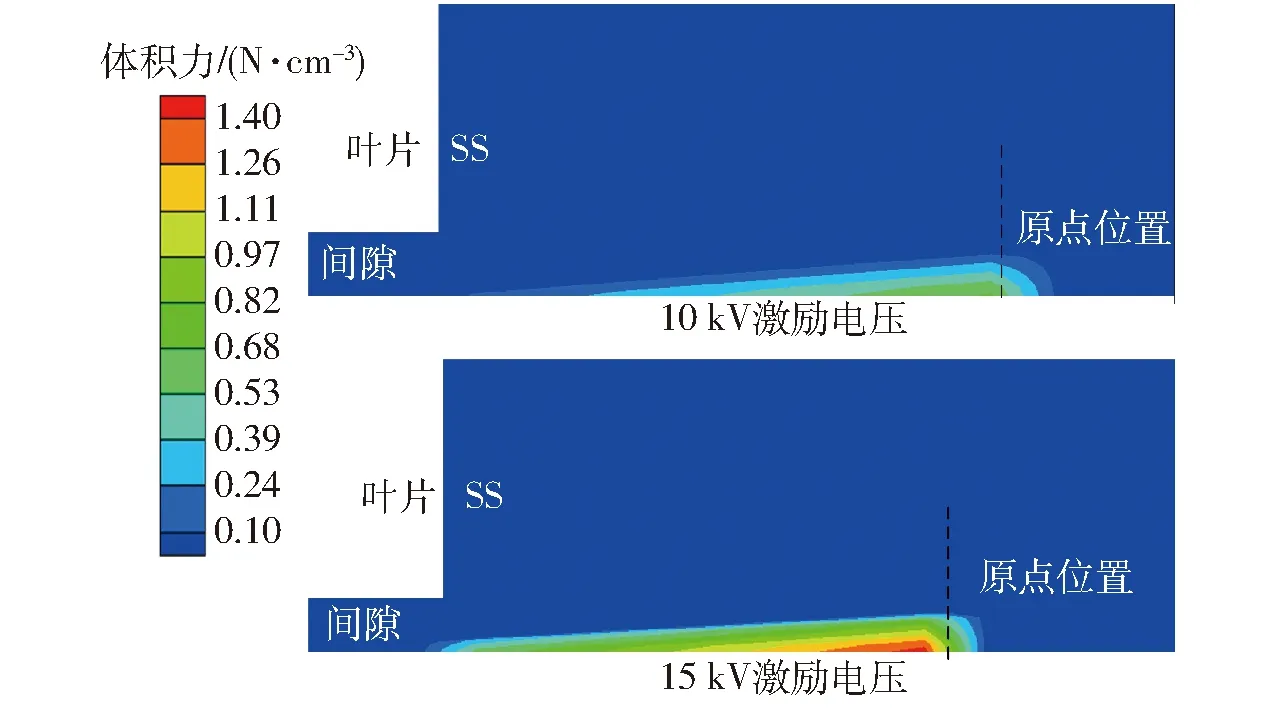
图9 等离子体激励诱导的体积力分布Fig.9 Body force distribution induced by plasma excitation

图10为不同等离子体激励电压下液环泵水力性能相对值的变化。纵坐标中的p和P分别表示施加等离子体激励后泵的进口真空度和轴功率；p0、P0、η0分别表示不施加等离子体激励的泵进口真空度、轴功率、效率。由图10可以看出，施加等离子体激励后，泵的进口真空度变化较小，而轴功率随激励电压的增大显著减小，导致泵的效率增大；上述结果表明等离子体激励可在一定程度上抑制液环泵叶轮轴向叶顶间隙泄漏流动，提升泵的性能。

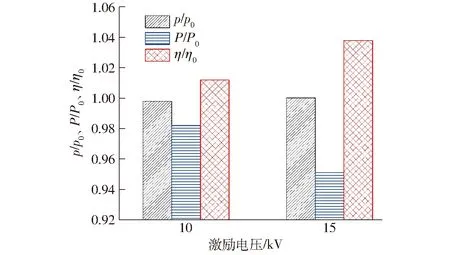
图10 不同激励电压下泵的水力性能Fig.10 Hydraulic performance of pump under different excitation voltages

图11为叶轮流道截面B、截面C的轴向近壁区域速度及其流线分布图。由图11b可以看出，等离子体激励能够在一定程度上改善液环泵轴向叶顶间隙泄漏流引起的二次流动。由图11a、11b可以看出，15 kV激励电压下，等离子体激励位置产生明显的壁面射流，其与间隙泄漏流的流向相反，反向壁面射流能够抑制泄漏流的强度；同时，在等离子体激励作用下，诱导激励位置产生旋涡结构。

由于等离子体激励器布置在泵侧盖内壁，随着叶轮的旋转，其与叶片之间的相对位置不断变化，因此不同激励位置对泄漏流动的抑制效果存在差异。由图11a可以看出，截面B中等离子体激励位置位于泄漏流下游，泄漏流速度较低，10 kV和15 kV激励电压均能有效抑制泄漏流强度。由图11b可以看出，截面C中等离子体激励位置位于泄漏流上游，泄漏流的速度较大，10 kV激励诱导的体积力较小，对间隙泄漏流的抑制效果不明显，但15 kV激励能够有效抑制间隙泄漏流强度。

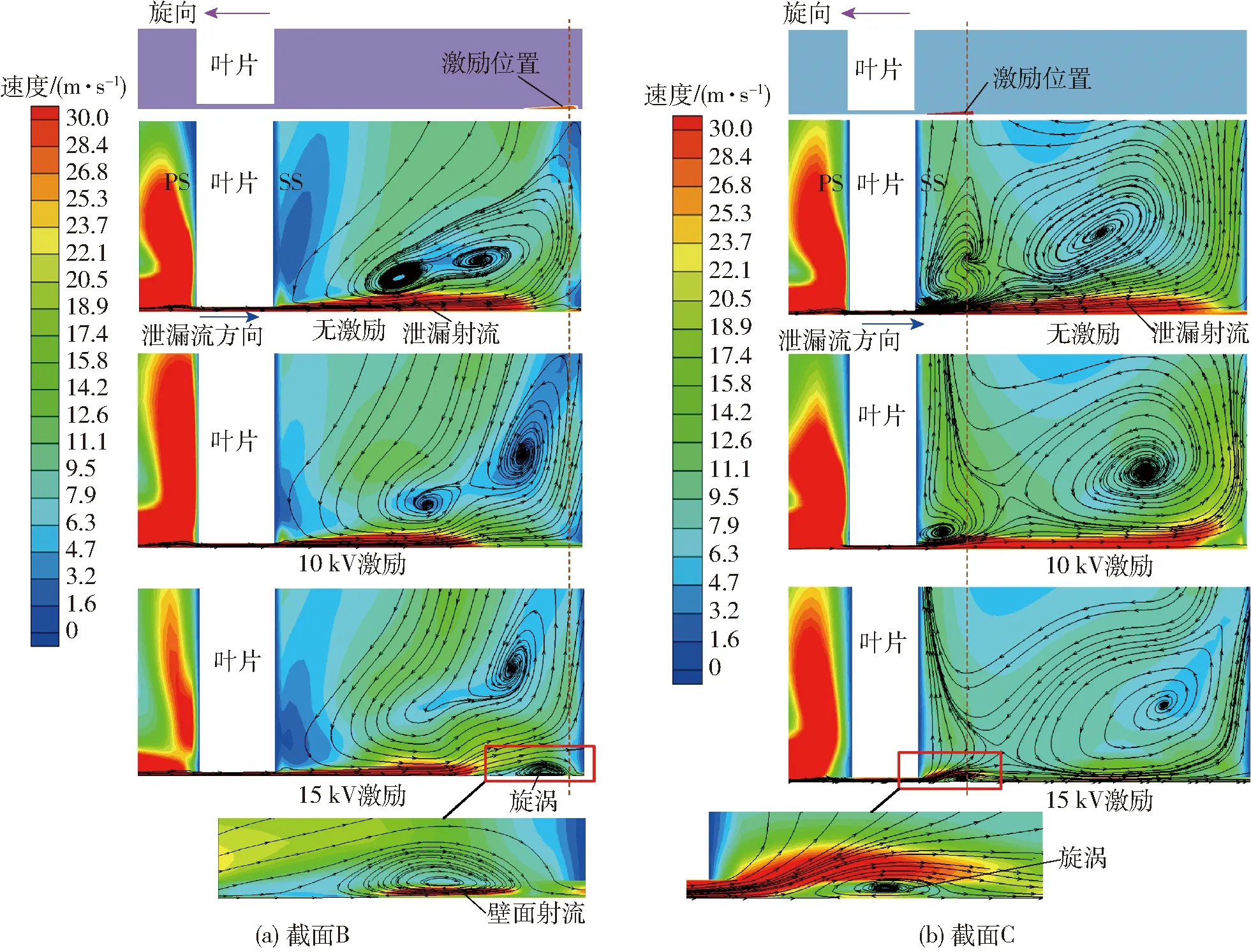
图11 截面B、C的速度分布及流线图Fig.11 Velocity distribution and streamline diagram of section B and C

为了分析等离子体激励沿叶片展向方向各截面上的泄漏流动抑制效果，选择叶轮内流道Ⅰ，并在流道Ⅰ的M叶片上垂直于叶片骨线沿展向均匀截取12个平面(S1～S12)，流道Ⅰ及各截面位置如图12所示。图13为液环泵叶轮流道Ⅰ内轴向近壁区域的湍动能分布。由图13a可以看出，液环泵轴向叶顶间隙泄漏导致流道近壁区产生较高的湍动能分布。由图13b、13c可以看出，15 kV激励电压下，流道近壁区的湍动能明显较10 kV低，表明15 kV电压下等离子体激励能够更有效地抑制间隙泄漏流动，降低间隙泄漏流动损失，其与图10中的水力性能变化相对应。

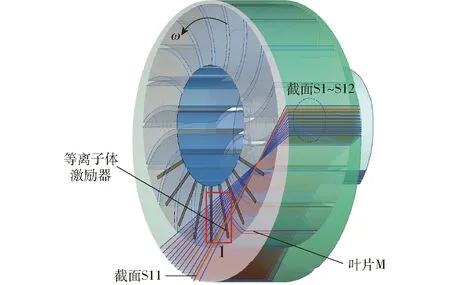
图12 湍动能分析的流道位置Fig.12 Position of channel Ⅰ for turbulent kinetic energy analysis

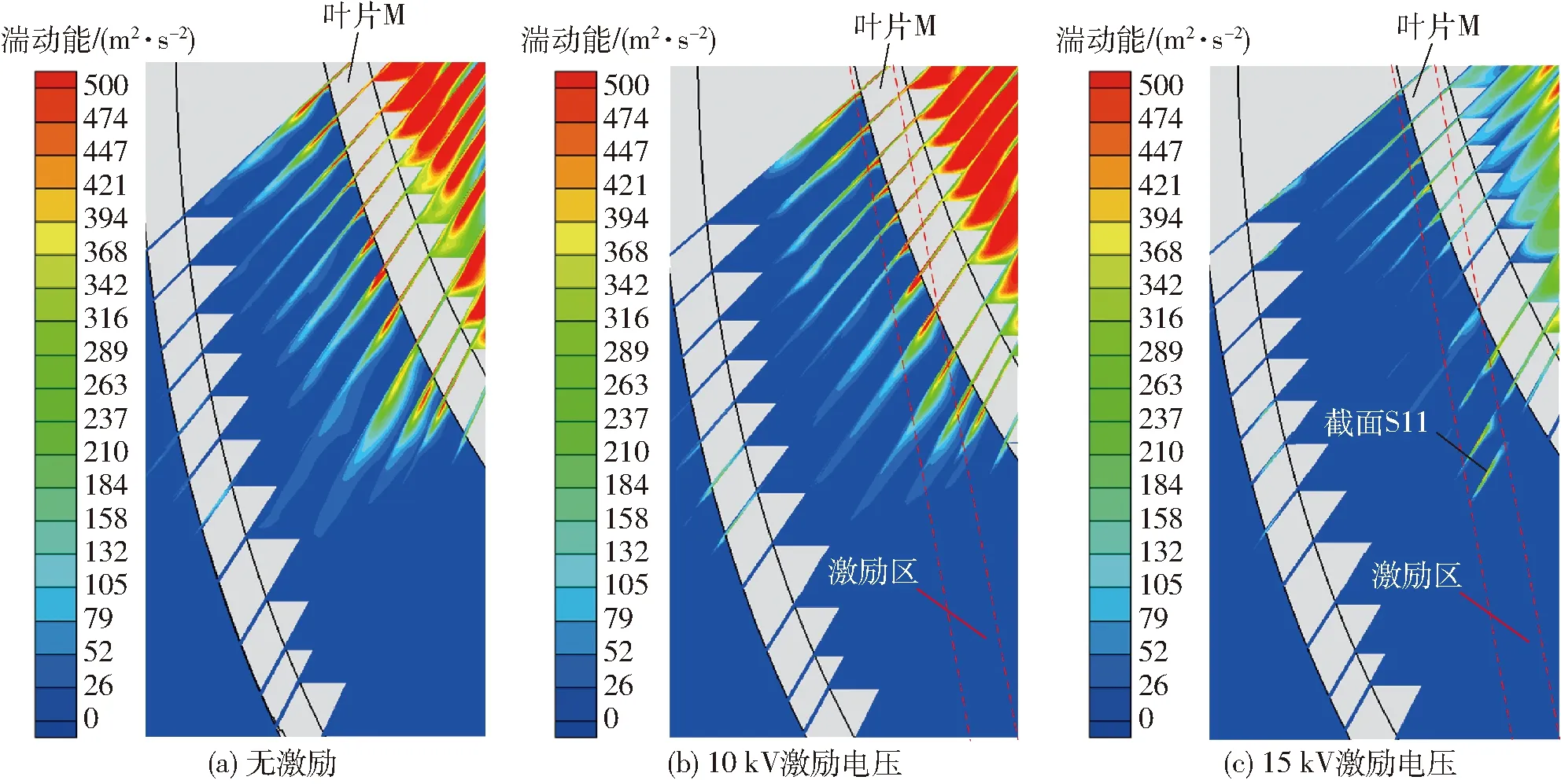
图13 流道Ⅰ内近壁区域的湍动能分布Fig.13 Turbulent kinetic energy distribution near wall in channel Ⅰ

图14为15 kV激励电压下流道Ⅰ内截面S11的近壁区域湍动能及流线分布图；由图14可以看出，等离子体激励位置具有较高的湍动能分布。结合图14和图11可以发现，在等离子体激励的非间隙区域，等离子体激励作用一方面能够产生反向壁面射流对间隙泄漏流动进行控制，同时在等离子体激励位置产生诱导涡结构，并引起流道近壁区域产生额外的水力损失。

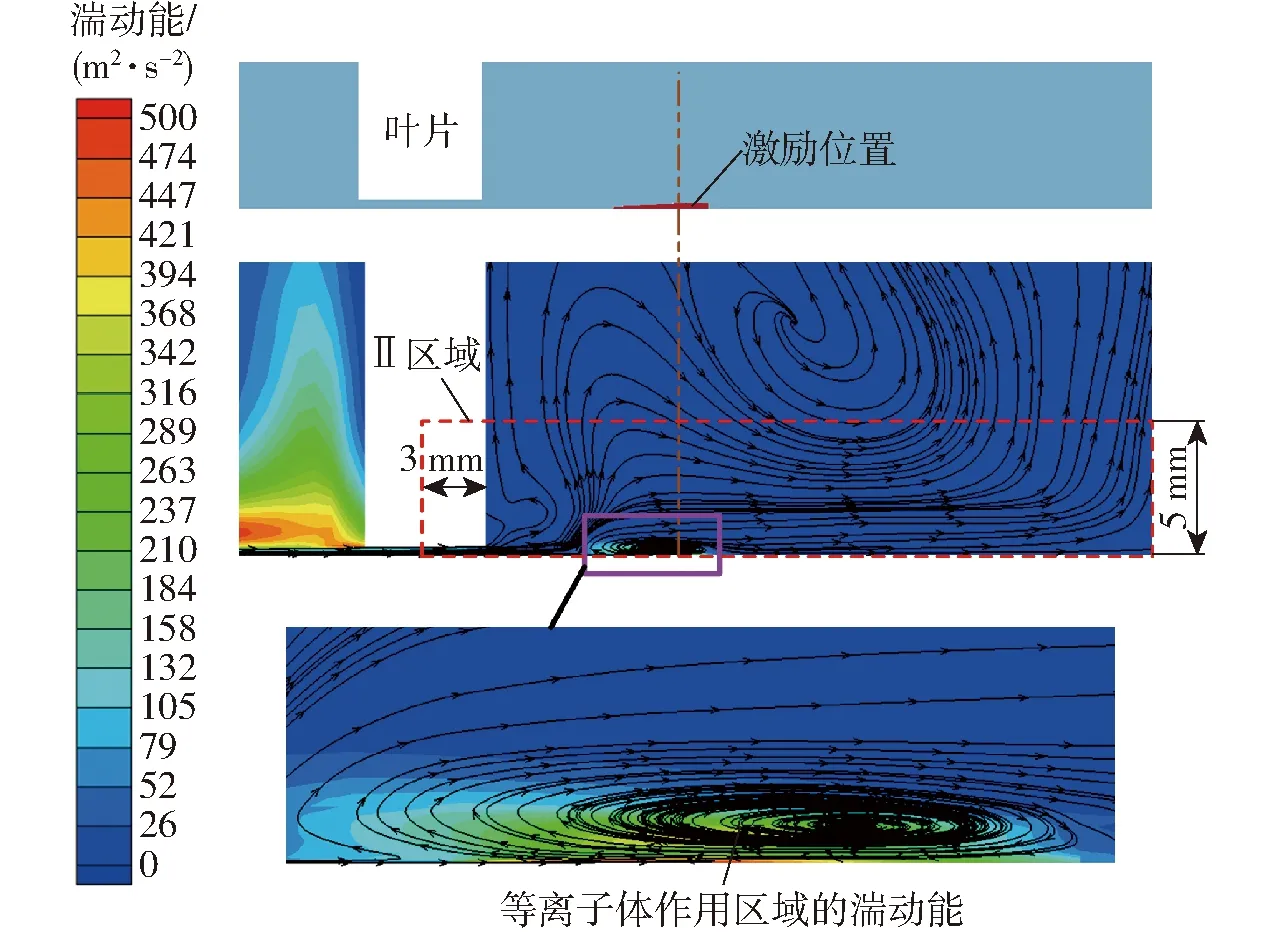
图14 等离子体作用区域的湍动能分布及流线图Fig.14 Turbulent kinetic energy distribution and streamline diagram in plasma action region

为了定量分析不同激励电压及位置对泄漏流动的抑制效果，将流道Ⅰ内叶片展向截面S1～S12的Ⅱ区域(图14)湍动能进行积分。图15为截面S1～S12近壁区域Ⅱ的湍动能相对值变化，纵坐标中的ε为施加等离子激励后的湍动能，ε0为不施加等离子激励后的湍动能。由图15可以看出，10 kV电压下，当激励位置靠近叶轮轮毂时，等离子体激励对泄漏流的抑制效果变差；15 kV激励电压的等离子体流动控制效果明显优于10 kV激励电压；15 kV电压下，当激励位置位于叶顶间隙出口附近时等离子体激励对间隙泄漏流具有较好的抑制效果。

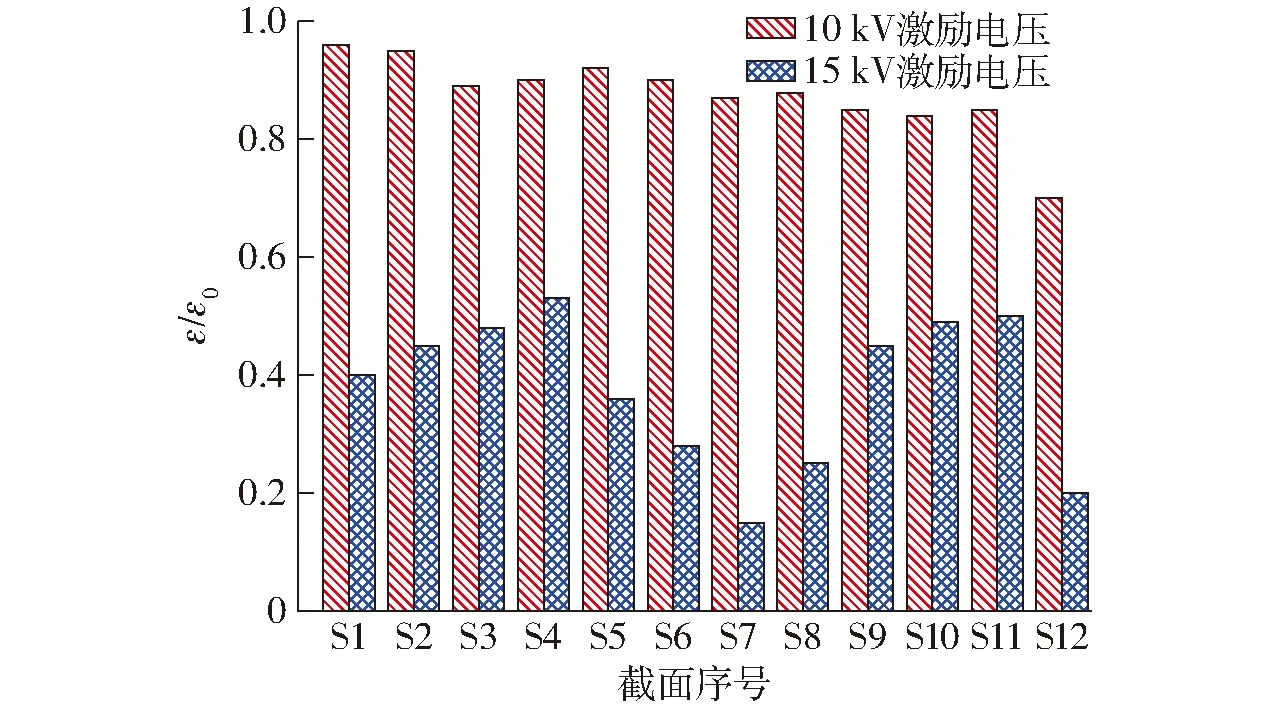
图15 流道Ⅰ内叶片展向截面近壁区域湍动能的相对值Fig.15 Relative values of turbulent kinetic energy in near-wall region of blade spanwise sections in channel Ⅰ

3 结论

(1)液环泵内排、吸区之间的压差作用导致排气区始端至吸气区末端区域出现明显的泄漏高速射流，其沿叶轮旋转的反方向流出间隙后，与叶轮主流相互作用并逐渐耗散。

(2)在等离子体激励作用下，等离子体激励诱导的壁面射流方向与间隙泄漏流方向相反，反向射流能够有效抑制间隙泄漏流强度，并在一定程度上改善由泄漏流引起的二次流动，同时在等离子体激励的非间隙区域，等离子体激励诱导近壁区产生旋涡结构，并引起一定的水力损失。

(3)等离子体激励对液环泵轴向叶顶间隙泄漏流动的抑制效果与激励电压及激励位置密切相关；15 kV激励电压的等离子体流动控制效果明显优于10 kV激励电压，当激励位置位于叶顶间隙出口附近时等离子体激励对泄漏流具有较好的抑制效果。