再生稻空间直取大偏移轮系宽窄行分插机构设计与试验

徐亚丹 诸杨华 薛向磊 王 磊 孙 良 俞高红

(1.杭州职业技术学院吉利汽车学院， 杭州 310018； 2.浙江理工大学机械与自动控制学院， 杭州 310018； 3.浙江省种植装备技术重点实验室， 杭州 310018； 4.浙江省农业科学院， 杭州 310018)

0 引言

再生稻是采用一定的栽培管理措施，使头季水稻收割后稻桩上的休眠芽萌发生长成穗而再收获一季的水稻种植模式[1-2]，已成为了我国光温资源一季有余两季不足稻区及“双改单”稻区提高复种指数、增加收获面积、稳定稻谷总产量的一种有效种植制度[3]。然而现有插秧机普遍采用300 mm的行距，与水稻收获机履带宽度及轨距不匹配，收获时无法避免对稻桩的碾压，不利于机械收获作业且影响下一茬产量[4]。虽然通过减小履带宽度、调整履带轨距可解决底盘对行碾压的问题，但过小的履带宽度必然增大履带底盘的接地比压，机器下陷严重，不适用于喂入量较大的收获机[5]。

在不改变传统插秧机秧箱结构、配套育秧流水线的前提下实现插秧机的宽窄行栽植[6-8]，即在等行距300 mm秧门下，完成宽行与窄行种植。解决该问题的关键在于研发一种具有空间直取秧、大偏移、小侧向穴口插秧轨迹的分插机构。井上强[9]针对日本水稻密植要求提出了通过更改平面分插机构在移栽机上的布置方式(秧门间距发生变化)来实现水稻密植，行间距由300 mm变为210 mm；小西达也等[10-11]突破平面运动轨迹的限制，研制了空间轨迹的毯苗摆臂式密植和锯齿形密植分插机构，解决了等秧门间距下的水稻密植问题，但这类分插机构结构复杂，未见推广应用。

国内农机企业根据宽窄行要求在秧箱中插入宽隔板改变秧箱宽度，并按宽窄行形式布置分插机构[12]。由于更改了传统移栽机的部件，且窄秧盘育秧与传统流水线育秧不匹配，因此难以大力推广。文献[13-15]在不改变传统育秧流水线的前提下设计了倾斜式宽窄行分插机构，改变了传动箱与分插机构之间动力连接方式，通过斜齿交错啮合、万向节连接、锥齿啮合等方式将分插机构斜置，不改变传统移栽机秧门的位置，其轨迹与地面形成“八”字形，达到宽窄行种植效果。但存在斜取秧伤根、取秧量不均匀等问题。孙良等[16-18]将空间非圆齿轮副引入行星轮系分插机构，提出了空间轨迹行星轮系分插机构设计思路。祝建彬等[19]设计了一种斜齿交错非圆锥行星轮系分插机构，实现了内偏式空间轨迹，同时满足直取秧和小穴口插秧要求，但在试验过程中发现，轨迹内偏式栽插大苗(苗高大于20 cm)时倒苗现象比较严重。

因此，为了更好地解决空间行星轮系式宽窄行分插机构设计兼顾直取秧式、轨迹向外大偏移、侧向小穴口的问题，同时实现宽行430 mm，窄行170 mm间隔栽插的设计目标，即侧向偏移量为65 mm的空间轨迹宽窄行分插机构设计需求，本文对基于移栽作业轨迹上若干关键点位姿信息的空间行星轮系机构进行研究，设计具有空间直取秧、侧向大偏移及小穴口宽窄行分插机构，以期解决再生稻生产过程中收获机履带碾压头季稻稻桩的问题。

1 移栽轨迹规划

再生稻宽窄行移栽轨迹特征如图1所示，水稻毯苗宽窄行分插机构的轨迹规划步骤为[20-21]：

图1 再生稻宽窄行移栽轨迹特征Fig.1 Characteristics of transplanting track of ratooning rice in wide and narrow rows

(1)“斜取秧”时秧针撕苗会影响周边秧苗的根须，还会造成取秧不均匀和在毯苗起始位位置和结束位置取不到秧苗的问题。取秧时刻秧针相对毯状苗的位置角δ，不仅影响毯苗两端秧块的均匀性，也易引起秧针与秧箱、秧门以及护苗板的干涉；而ε是由于取秧过程中秧针运动轨迹倾斜所致，ε越大秧爪对秧根的损伤越严重，影响秧苗返青，从而影响产量。因此在设计再生稻宽窄行行星轮系分插机构时，为保证秧苗从秧箱顺利取出并减少伤苗率，达到“直取秧”效果，从结构设计的角度上减小δ，使其在取秧时刻正对秧门(δ=0°)，在规划空间移栽轨迹时尽量减少取秧阶段秧针在z向距离上的偏移以此减小ε，即：轨迹位置1到位置2表示秧针取苗阶段，其z向偏移量满足0≤|z2-z1|≤5 mm；位置2到位置3表示秧苗在护苗器中的夹紧过程，其z向偏移量满足0≤|z3-z2|≤10 mm。

(2)推秧时秧针与y轴的夹角(推秧侧向偏角γ1)影响秧苗直立度，角度过大秧苗容易倒伏。在保证直取秧的前提下(秧针在位置1正对秧门)，推秧侧向偏角γ1应在0°～20°。

(3)从位置1到位置3表示秧针完成取苗且秧苗被夹苗器夹紧这一过程，为避免移栽臂发生大幅度转动与护苗板干涉损坏秧苗，在此阶段秧针姿态位移变化需尽量小。所以从位置1到位置3轨迹的z向偏移量应尽量小，满足0≤|z3-z1|≤15 mm；而从位置1到位置5所表示的轨迹总偏移量与宽窄行的偏移量有关，本文所涉及的水稻宽窄行移栽模式宽行行距430 mm，窄行行距170 mm，即取苗点1到推苗点5的z向偏移量为z5-z1=65 mm。

(4)为了保证植苗效果，分插机构在运动过程中，移栽轨迹形成的前进穴口长度(x′6-x′4)应在10～25 mm之间；侧向穴口宽度(z6-z4)应在10～30 mm之间。

(5)在分插机构运动过程中，为保证秧苗的株间距，秧苗栽植距离L应在180～200 mm之间；为防止秧苗被移栽臂推倒，动轨迹所形成的环扣高度H应大于秧苗高度。

水稻移栽质量与移栽臂在取苗起始、取苗结束、推苗这3个关键位置的姿态密切相关。这3个位姿点分别对应图1中的点1、3、5。根据图1所示参考系，可用4×4的齐次矩阵描述这3个点的位置与姿态[22-24]，本文将通过这3个空间位姿点求解再生稻毯苗宽窄行分插机构的参数。

2 空间2R机构运动综合模型

若不考虑齿轮副约束，如图2所示，将单行星架空间轮系分插机构简化为空间开链2R机构[25]。l1为轮系的行星架长度，即太阳轮轴心到行星轮轴心的距离；l2为行星轮轴心到移栽臂秧针尖点C的距离。G=(G，A×G)和W=(Wi，Bi×Wi)分别表示分插机构的输入轴和输出轴，其中G为输入轴的方向向量，A为输入轴上的一点，Wi为输出轴的方向向量，Bi为输出轴上的一点，A和Bi分别为两轴的公垂线与各自轴的交点，输入轴和输出轴的夹角为σ。机构运动时，杆件1绕输入轴G转动，杆件2相对杆件1绕着输出轴W转动，在输入轴和输出轴的共同作用下移栽臂秧针尖点C形成轨迹M。

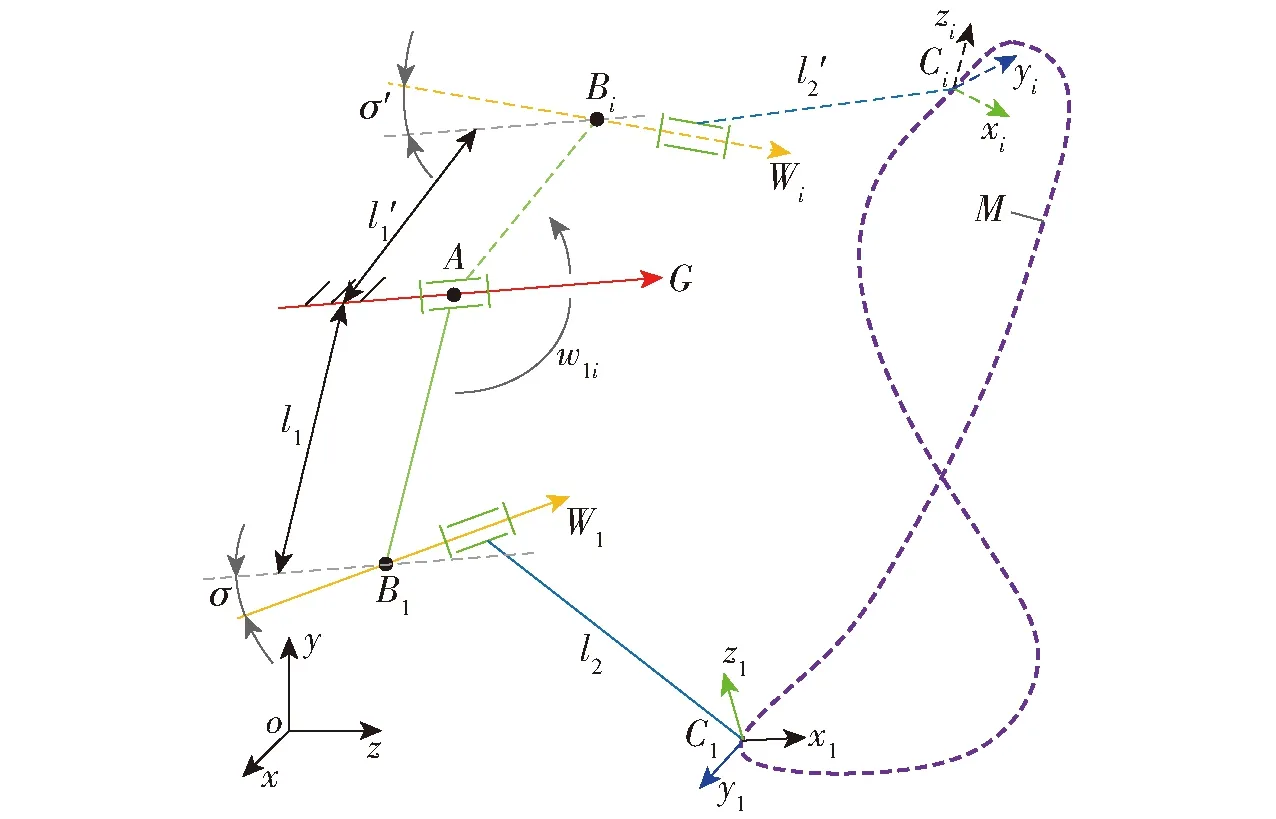
图2 空间2R机构运动轨迹图Fig.2 Trajectory diagram of spatial 2R mechanism

Ci(i=1,2,…,n)表示轨迹M上的点，选定n个点设计其位姿为

(1)

式中Ri——3×3姿态矩阵

di——3×1位置向量

选第1个位姿点T1为参考点，空间开链2R机构从C1运动至Ci(i=2,3,…,n)的刚体相对位移矩阵表示为

(2)

空间2R机构在运动过程中，根据其输入轴G与输出轴Wi的交错角σ恒定不变，即σ=σ′，得到角度约束方程

(3)

机构在转动过程中始终保持杆长不变(l1=l′1)，得到定杆长约束方程

(B1-A)T(B1-A)=(Bi-A)T(Bi-A)
(i=2,3,…,n)

(4)

直线BA的运动平面应同时垂直于两转动轴线，即

GT(Bi-A)=0 (i=1,2,…,n)

(5)

(6)

其中Bi=T1iB1,Wi=R1iW1(i=2,3,…,n)。

为保证G轴与Wi轴夹角方向恒定，需要增加等矩约束方程

GT[(B1-A)W1]=GT[(Bi-A)Wi]
(i=2,3,…,n)

(7)

根据方向余弦公式，输入轴G的方向向量G、转动轴Wi的方向向量Wi都应满足方向向量约束

GGT-1=0

(8)

(9)

分析可知，空间2R链由输入轴G和输出轴W1以及它们的公垂线与各自的交点A、B1定义，将其设为G=(gx,gy,gz)，W1=(wx,wy,wz)，A=(ax,ay,az)，B1=(bx,by,bz)。建立含有12个未知参数的空间2R机构约束方程，因为等距约束方程(7)中含有定杆长约束方程(4)，所以在联立约束方程时只需建立等矩约束方程即可。联立方程(3)、(5)～(7)可得4n个约束方程。当n=3时约束方程个数等于未知数个数，可实现空间2R机构参数的精确求解。

3 分插机构设计

3.1 分插机构参数求解

依据水稻毯苗宽窄行分插机构取苗、带苗、植苗等动作设计要求，确定移栽臂在取苗起始、护苗结束、推苗这3个关键位置时的4×4位姿齐次矩阵T1、T2、T3：其中T1、T2共同约束取苗过程(包括秧针在夹苗器内)的轨迹姿态特征，T3主要约束推苗位置、推苗角以及推苗姿态变化。

在全局坐标系下具有xi、yi、zi3个局部坐标轴描述其姿态，在全局坐标系下xi的投影与x、y、z坐标轴的夹角表示为1×3的向量Rxi，同理可得Ryi、Rzi。di表示在全局坐标系下点的位置，如表1所示。

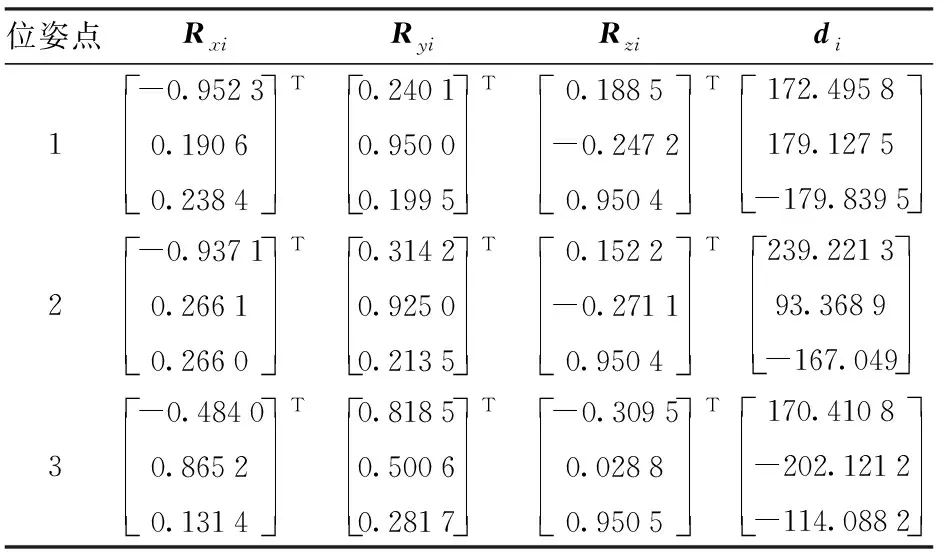
表1 关键3位姿点的参数Tab.1 Parameters of key three pose points

将T1、T2、T3代入开链2R机构的约束方程组，利用多胞体同伦算法软件HOM4PS 2.0求解获得空间2R机构参数的2组实数解，如表2所示。综合考虑分插机构行星架安装位置和移栽臂尺寸等要求，选择第一组解为初始设计参数。

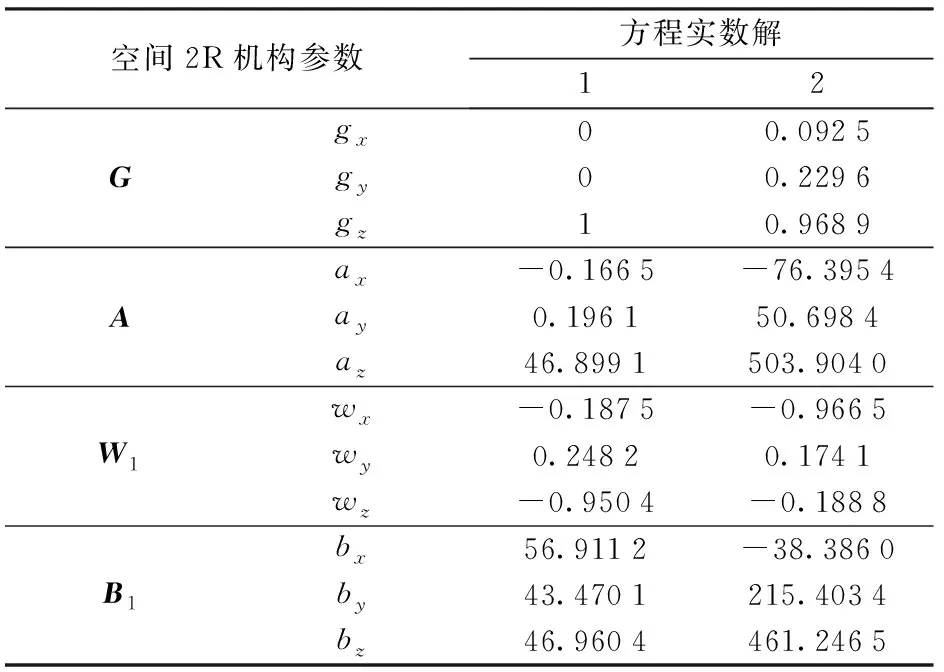
表2 方程参数实数解Tab.2 Real number solutions of equation parameters

但该组解中杆1长度lAB1=71.63 mm，杆2长度lB1C1=275.89 mm，杆2长度不合理的情况下若设计成移栽臂易发生干涉现象。因此需要沿空间2R机构的输入轴G建立投影平面Q(图3)，固定点A在平面Q上的投影为点Qo，将铰链点Bi沿着转动轴Wi的方向投影到平面Q上形成点Qi，连接Qo和Qi即为新的杆1杆长L1(行星架长度)，连接点Qi和Ci即为杆2杆长L2(移栽臂长度)。显然，此机构与求解模型是同一种运动学模型，具有相同的运动学特性。实数解2无法沿G轴移动平面Q得到合理的新的杆长L1、L2，而舍去这组解。

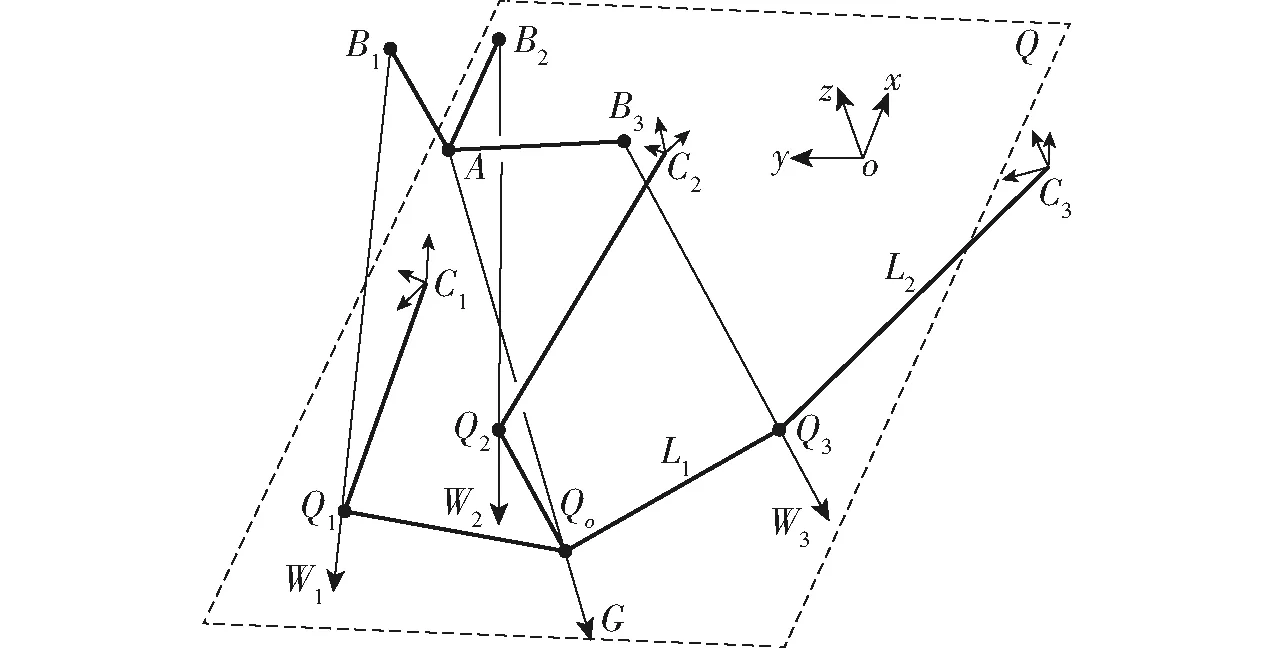
图3 空间2R机构参数确定Fig.3 Determination of parameters of spatial 2R mechanism

选择在距离点A位置312.89 mm建立平面Q。最终获得杆长参数为：L1=98.67 mm，L2=166.75 mm，输入轴G与输出轴Wi的夹角σ=18.13°。

3.2 分插机构轨迹复演与分析

在设计行星轮系式分插机构时，参考空间交错轴齿轮传动的组合形式，选定非圆齿轮-斜齿轮这种简单的传动组合形式，如图4所示。

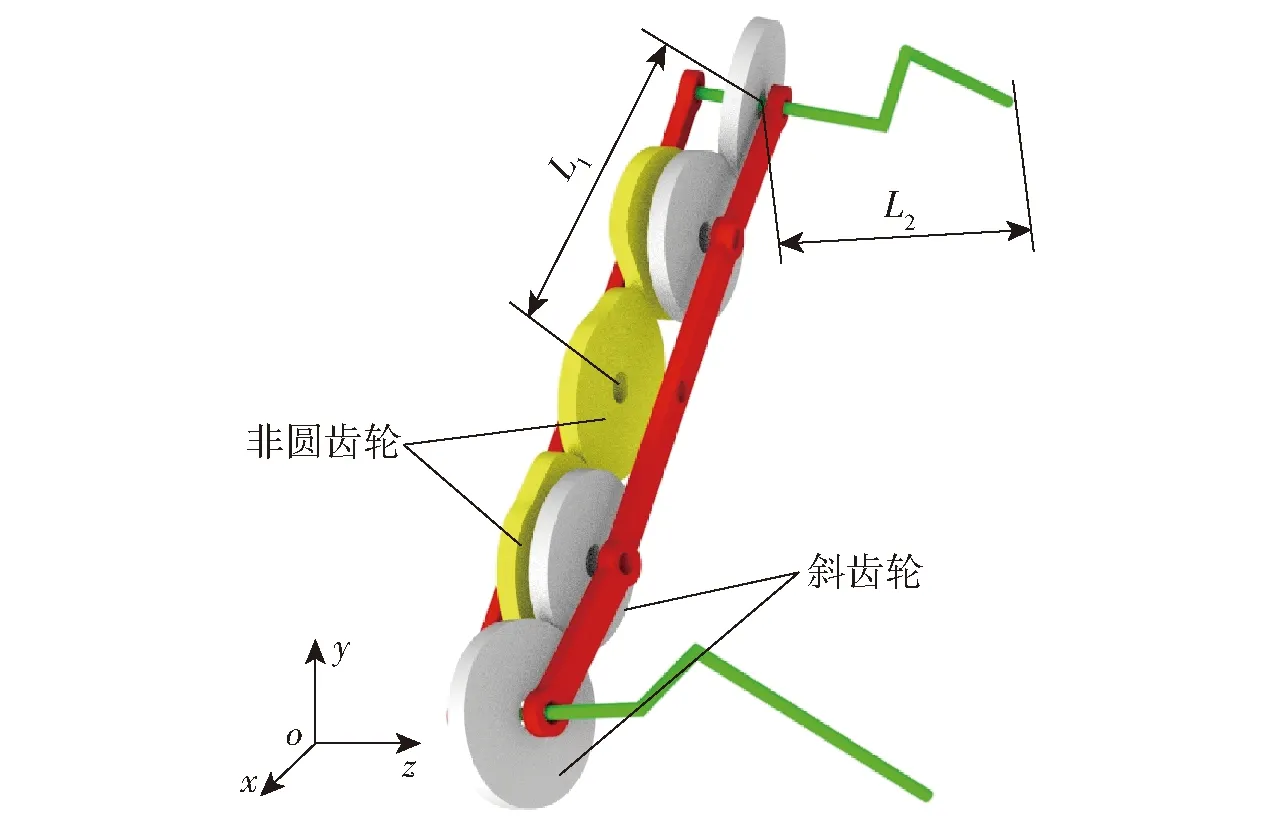
图4 宽窄行轮系分插机构Fig.4 Transplanting mechanism of wide and narrow gear train

在杆长不变的情况下，构建空间2R机构并复演末端点C的轨迹，空间2R机构可依次经过点Ci(i=1,2,3)。图5a为空间2R机构在xoy平面的复演情况，图5b为空间2R机构在yoz平面的复演情况。再生稻宽窄行行星轮系分插机构的行星架(杆1)在一个转动周期(0～2π)内作匀速转动，而移栽臂(杆2)相对行星架(杆1)作变速转动。由于行星轮系式分插机构移栽臂和行星架之间的运动不能出现回转现象，所以回转周期内两者的相对角位移需具有单调性。如图5所示，杆2与杆1的相对角位移为单调的情况下，灰色区域为2R机构的工作空间；轨迹线1、2、3分别为不同单调相对角位移下，空间2R机构形成的空间移栽轨迹。

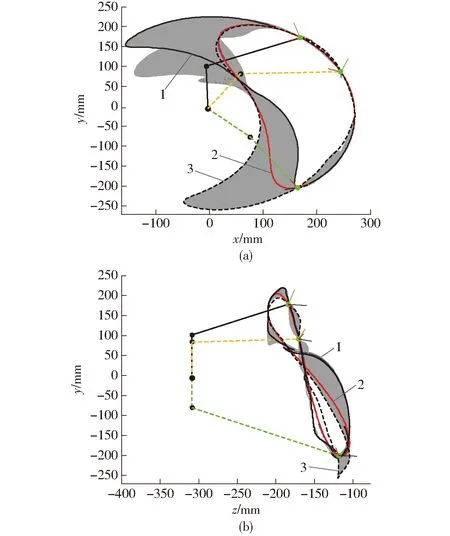
图5 分插机构可行域Fig.5 Feasible area of transplanting mechanism

图5中3条移栽轨迹线分别对应的相对角位移和传动比曲线如图6、7所示。如图6所示3条轨迹线的相对角位移均单调且都经过给定的关键3个位姿点；由图5可知，轨迹线1空回程段弧度过大，有可能造成移栽臂与秧箱的碰撞，且在推苗时侧向穴口较大。轨迹线3在推苗后继续向下运动，轨迹最低点后移，影响植苗效果；如图7所示，轨迹线1的传动比差值较大，轨迹线3的传动比波动较多，均不利于非圆节曲线的生成，非圆齿轮凹凸性较差。综合移栽轨迹和传动比，最终选择轨迹线2作为符合设计要求的移栽轨迹。

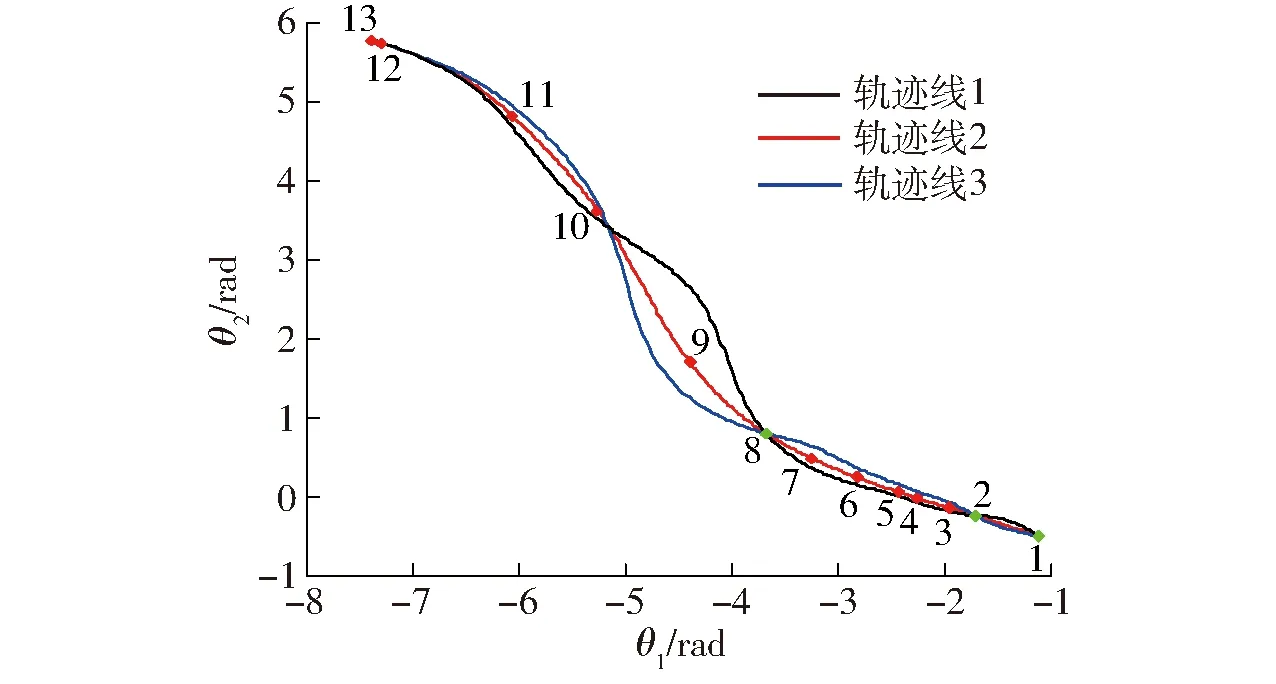
图6 相对角位移曲线对比Fig.6 Comparison of relative angular displacement curves

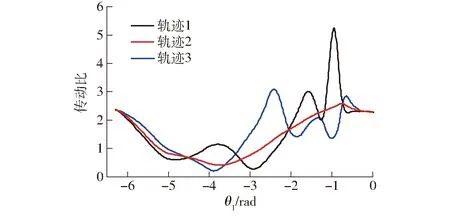
图7 传动比曲线对比Fig.7 Comparison diagram of transmission ratio curve

3.3 非圆齿轮节曲线优化

通过机构总传动比I和一级非圆齿轮中心距L1/2得到非圆齿轮曲率半径ρ，根据ρ可判别非圆齿轮的凹凸性[26]。

经计算，太阳轮凸性指标p1∈[-0.504 7,2.576 0]，中间非圆齿轮的凸性指标p2∈[-0.503 0, 2.578 5]，因此选取p1=-0.504 7作为一级非圆齿轮的凸性指标，并在此数值附近寻找其他凸性指标差的点。根据这些点反推到传动比所对应的点，进而找到相对角位移曲线上所对应的点，其所在区域在图6轨迹线2中型值点3～4之间、5～6之间和6～7之间。

在凸性较差点对应的角位移型值点所在区域，分别设置3个黑心点X1、X2和X3。调节这3个型值点的横坐标达到优化非圆齿轮节曲线的效果。根据角位移曲线的单调性，该3个型值点横坐标满足

式中μi——角位移曲线中型值点3～7横坐标

可以计算X1、X2和X3对应点及其附近的向径之差并建立优化目标函数

f(X1,X2,X3)=Y

其中

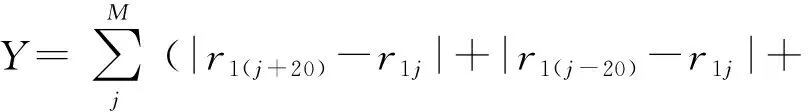
其中r1(j+20)-r1j和r1(j-20)-r1j分别表示太阳轮节曲线上第j点与附近两个点的向径之差；r2(j+20)-r2j和r2(j-20)-r2j分别表示中间轮非圆齿轮节曲线上第j点与附近两个点的向径之差。

适应度函数的收敛性和每代对应的适应度如图8所示。如表3所示，通过多次优化计算和数据结果筛选最终得到的一组最优值，X1、X2和X3的上下限值分别为图6所示的角位移曲线上型值点3～4之间、5～6之间和6～7之间的横坐标。

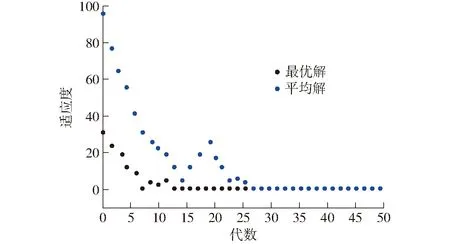
图8 遗传算法适应度Fig.8 Convergence diagram of genetic algorithm

表3 遗传算法优化后参数值Tab.3 Parameter values optimized by genetic algorithm rad

得到太阳轮凸性指标p′1∈[0.404 5,2.576 0]，中间非圆齿轮凸性指标p′2∈[0.413 0,2.578 5]，因此选取p′1=0.404 5作为优化后一级非圆齿轮凸性指标，与上述所得凸性指标p1=-0.504 7比较，从图9可以看出，优化后相对角位移曲线变化不明显；从图10可以看出，非圆齿轮节曲线的凸性变好，圆度变优。

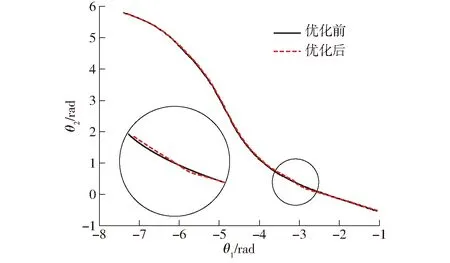
图9 优化前后角位移对比Fig.9 Comparison of angular displacement before and after optimization

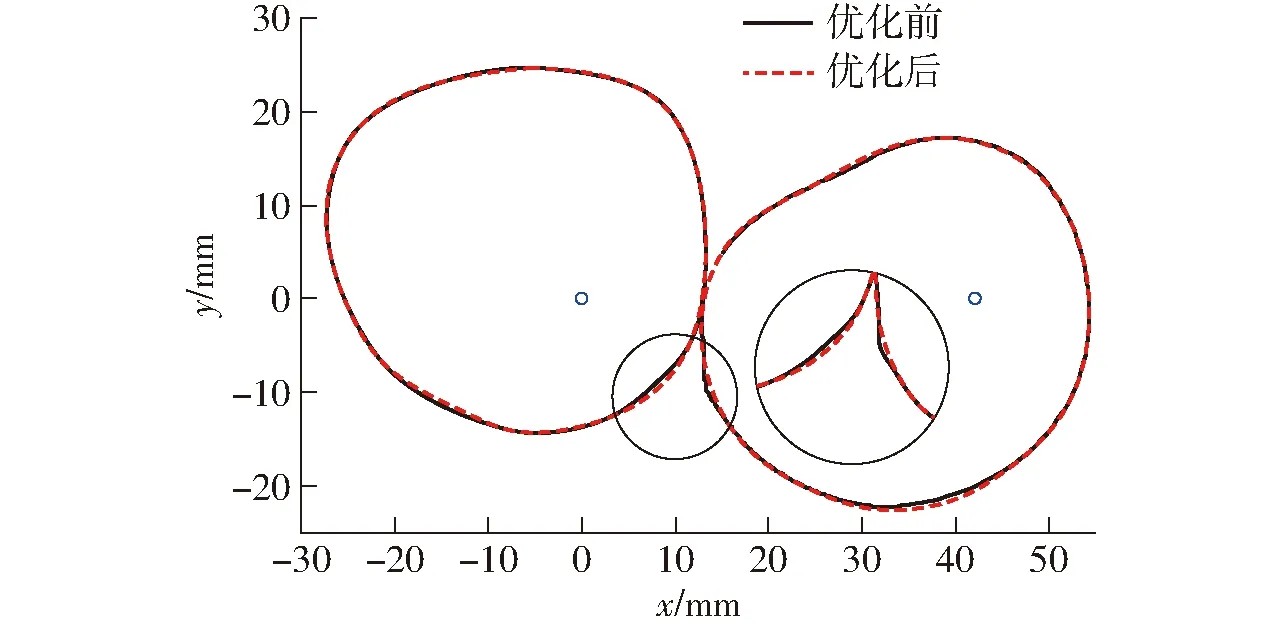
图10 优化前后节曲线对比Fig.10 Comparison of pitch curves before and after optimization

利用优化后的参数复演移栽轨迹。如图11所示，移栽轨迹在优化目标区域发生明显变化：xoy平面内轨迹更为圆滑，yoz平面内轨迹的侧向穴口略微增大。虽然优化后移栽轨迹发生变化，但优化轨迹经过给定的空间3个关键位姿点；虽然侧向穴口略微增大，但这些变化在可接受范围内。

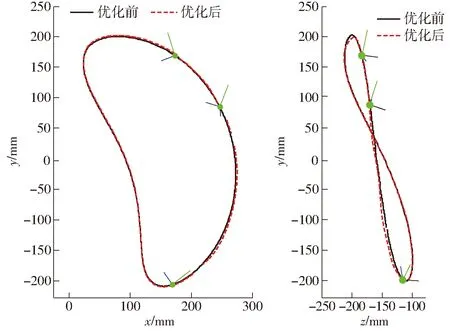
图11 优化前后移栽轨迹对比Fig.11 Comparison of transplanting trajectories before and after optimization

4 分插机构仿真与试验

4.1 轨迹与姿态验证

对机构进行虚拟仿真，当分插机构处于取秧阶段，移栽臂取苗角α1为1°；当分插机构取苗结束离开夹苗器时，移栽臂角度α2为26.54°，且该点与取苗点的z向偏移量ΔS2为13.34 mm；分插机构在推苗过程中，移栽臂推苗角α3和推苗侧向角γ1分别为75.26°和16.13°，移栽轨迹取苗点和推苗点的z向偏移量ΔS1为65.59 mm，分插机构形成的侧向穴口宽度ΔS3为23.69 mm。对比图12与图11发现，秧针末端尖点形成的移栽轨迹与优化后的理论轨迹基本一致，仿真所得分插机构空间关键3位姿及移栽轨迹与理论数据基本一致，从而验证了分插机构仿真的正确性。

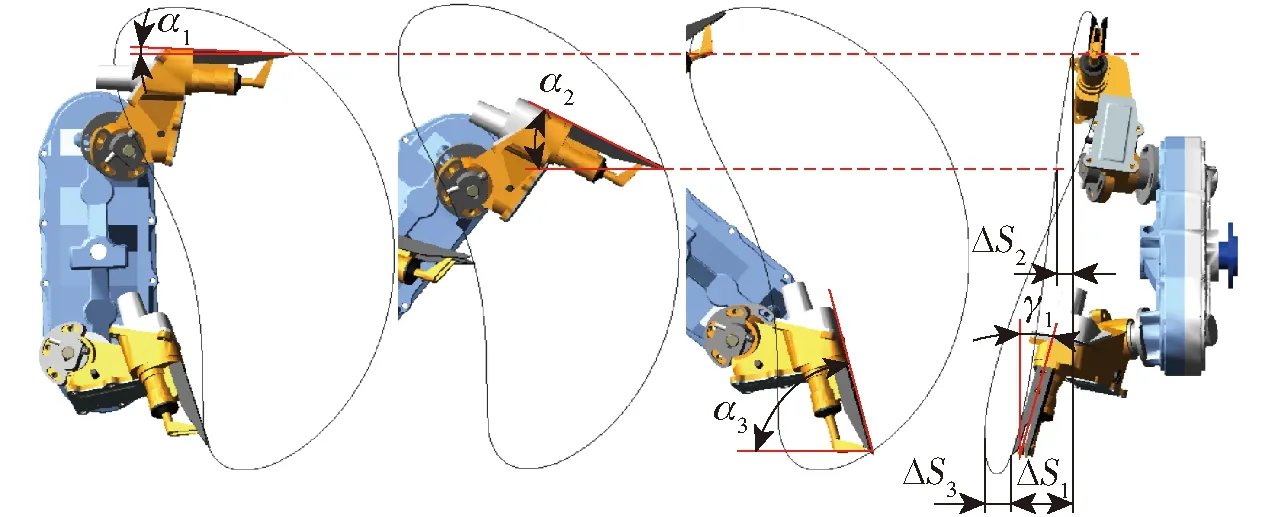
图12 移栽机构关键3位姿仿真Fig.12 Simulation of key three positions and postures of transplanting mechanism

在空转试验过程中用高速摄像机分别在空转试验台正面及侧面跟踪拍摄移栽臂秧针尖点的位置和姿态，记录拍摄实物样机在xoy平面和yoz平面的运动轨迹。然后将生成的视频导入图像视频后处理软件PCC，以移栽臂秧针尖点为追踪目标点，逐帧描绘其在高速运转情况下所形成的空间移栽轨迹。如图13所示，将实际空间移栽轨迹图像导出并与虚拟样机仿真轨迹进行对比分析，发现二者形状基本一致。比较宽窄行轮系分插机构的空间移栽轨迹与理论轨迹、虚拟样机仿真轨迹，发现轨迹形状基本一致。存在细微的偏差可能是由于齿轮间隙、加工精度、装配误差等问题导致，偏差在合理范围内。空转试验验证了基于空间移栽轨迹关键3位姿的宽窄行轮系行分插机构参数反求方法正确性和机构设计可行性。

图13 实际轨迹与仿真轨迹对比Fig.13 Comparison between actual trajectory and simulation trajectory

4.2 取苗试验

试验时将毯苗放置在秧箱上，将装配好的样机安装在试验台上，调节试验台电机的输出转速以控制再生稻宽窄行分插机构在转速45、60、90 r/min下取苗，因设计的分插机构为双臂式，所以取苗速度为90、120、180次/min。

通过高速摄像机拍摄实际移栽过程中秧针的位置姿态(图14)，利用PCC视频处理软件中的两点法测角度，以x轴正向为基准测得的仿真角度分别为179.12°、103.26°和73.55°，经过换算得到实际取苗角、推苗角、推苗侧向偏角和取推苗差角分别为0.88°、76.74°、16.45°和75.86°，与仿真角度(1°、75.26°、16.13°和74.26°)基本一致，验证了分插机构取推苗位姿满足设计要求。

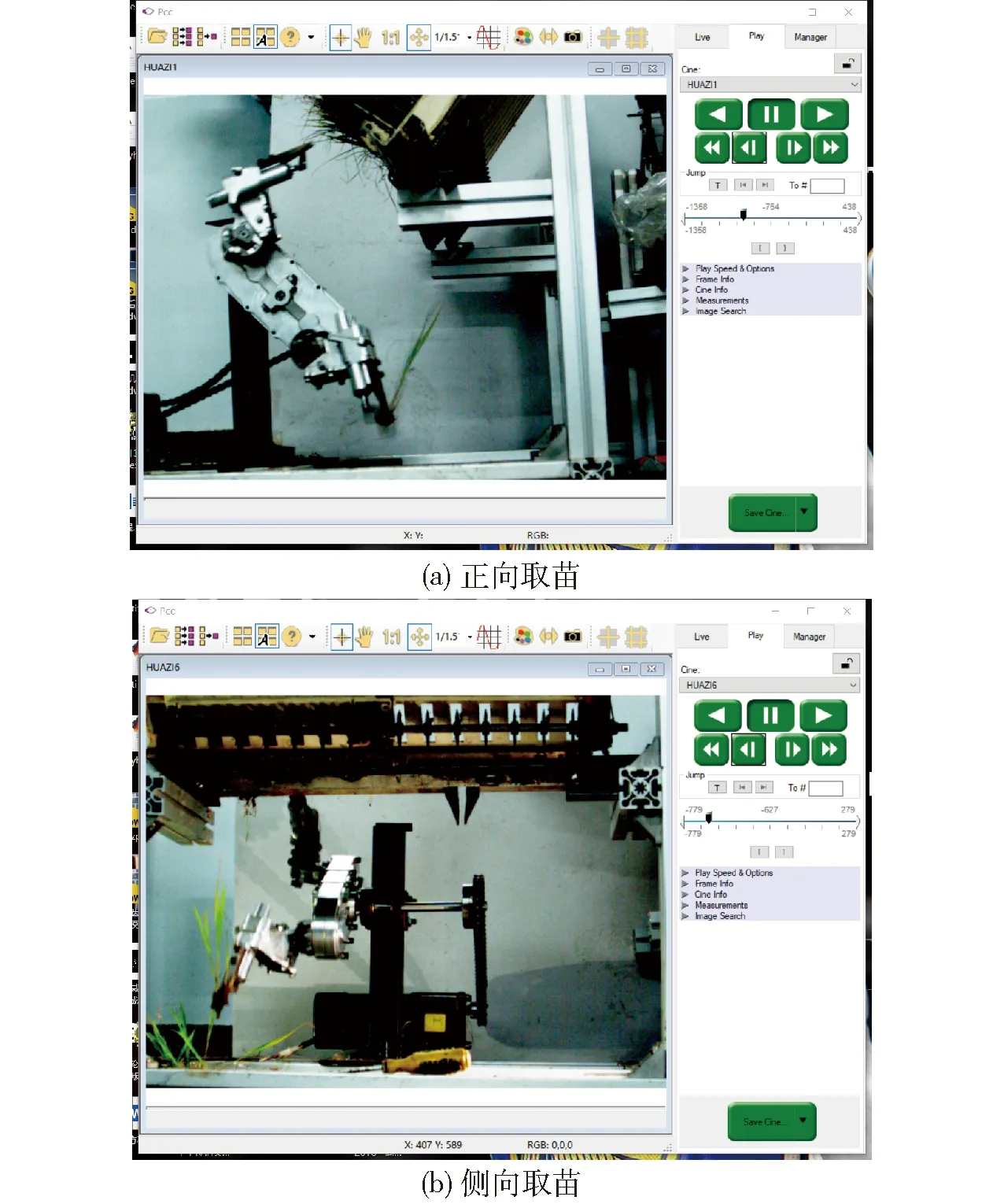
图14 取苗试验高速摄像结果Fig.14 High-speed camera results of taking seedling tests

5 结论

(1)根据再生稻大偏移量宽窄行插秧种植要求，规划设计了符合要求的空间移栽轨迹；并以其上3个关键位姿数据为约束，建立了空间2R开链机构几何约束求解模型，采用同伦算法求解得到符合要求的机构参数。

(2)基于求解得到的机构参数，拟合得到开链机构输入与输出轴相对角位移曲线，确定机构总传动比，复演得到满足移栽要求的空间轨迹，并基于遗传算法对非圆齿轮节曲线进行了优化，在不改变关键轨迹段的情况下得到了合理的非圆齿轮节曲线。

(3)设计了一种非圆齿轮与交错斜齿轮组合传动的空间行星轮系宽窄行分插机构，虚拟仿真与样机试验结果表明，机构实际运动轨迹姿态与理论设计基本一致；其取苗至推苗横向偏移量ΔS1为65.59 mm、侧向推苗角γ1为16.13°、侧向穴口宽度ΔS3为23.69 mm，满足再生稻宽窄行移栽要求，验证了轮系式宽窄行分插机构设计可行性。