基于改进二进制粒子群优化的有源配电网优化方法

杨军， 赵通， 赵宇坤， 高梦妍， 陈慧娜， 姚威宏

(北京石油化工学院 信息工程学院，北京 102617)

0 引 言

配电网是国民经济和社会发展的重要公共基础设施，含分布式电源的配电网能够弥补集中输发电的不足，最大限度利用多种能源[1]。但分布式电源大规模渗入后，导致配电网有源变无源，潮流的大小和方向发生改变，以及电压稳定性发生变化[2]，研究含分布式电源的配电网运行方式优化非常有意义。

由于开关组合方案的多样性，导致有源配电网优化问题是一个多目标、非线性NP难问题[3]。文献[4]以网损最小为目标函数，将改进的教与学优化算法应用于配电网供电路径快速优化。文献[5]通过重新定义二进制粒子群算法的自适应度值，实现含分布式电源配电网故障定位。文献[6]以改善系统网损、实现负荷均衡和减小电压偏差为目标函数，在传统萤火虫算法的基础上进行改进，提高了局部寻优能力和全局搜索能力。由于配电网优化问题是具有二进制求解空间的离散优化问题，可以采用二进制粒子群优化(binary particle swarm optimization, BPSO)[7]搜索最优方案。

本文提出一种基于自适应变异BPSO算法的配电网优化方法。在模型方面，增加对开关操作次数和孤岛效应的约束；在算法方面，提出新型的转换函数和变异操作，使其在全局搜索和收敛速度方面进一步提升，通过仿真验证了该方法的合理性和优越性。

1 配电网优化数学模型

1.1 目标函数

(1)有功网损:

(1)

式中：N为支路总数；Pi和Qi分别为第i条支路的有功与无功功率；Ui为第i条支路的末端节点电压；Ri为第i条支路的电阻；ki为第i条支路的开关状态，0代表断开，1代表闭合；Pmin为总有功损耗。

(2)负荷均衡:

(2)

式中：m为闭合的支路总数；Sj和Sjmax分别为第j条支路注入的复功率和最大允许复功率；f1为负荷均衡度。

(3) 电压偏差：

(3)

式中：t为节点编号；k为节点总数；Uts、UtN分别为第t个节点的实际电压与额定电压；f2为电压偏移量。

1.2 约束条件

(1)潮流约束:

(4)

(5)

式中：PGi和QGi分别为第i个节点分布式电源注入的有功与无功功率；Vi为第i个节点的电压幅值；Gij、Bij、θij分别为节点i、j之间的电导、电纳和电压相角差。

(2)节点电压约束：

(6)

式中：Uimin、Uimax分别为节点i允许的最小和最大电压幅值；Ui为节点i电压值。

(3)支路电流约束：

(7)

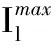
(4)网络拓扑约束:

gk∈Gk

(8)

式中：gk为经优化后的拓扑结构；Gk为迭代后所有满足辐射状要求的拓扑结构集合。

2 算法设计

2.1 基本二进制粒子群算法

在BPSO中，粒子速度按照式(9)更新。

(9)

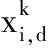
粒子位置更新公式为：

(10)

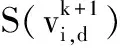
(11)

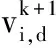
2.2 改进二进制粒子群算法

BPSO的转换函数可分为S-型、V-型两种类型。V-型系列的转换函数具有较大优势[8]，设计的转换函数如式(12)所示。

(12)

基于以上转换函数T(·)，二进制位置的更新过程也要进行相应改进，采用式(13)对二进制位进行更新。

(13)

采用以上位置更新公式，BPSO易陷入局部最小的问题仍然没有得到有效解决。因此引入变异操作使粒子的二进制位置以给定的变异率转换到它的相反值。对第i个粒子在第d次迭代中第k维的位置值来说，变异操作可由式(14)表示。

(14)

式中：rmu为变异率，它决定了二进制位转变为其相反值的概率。粒子中的每个二进制位都以相同的概率rmu从1变为0或者从0变为1。

3 仿真分析

3.1 仿真参数设置

为验证算法有效性，以IEEE 33节点系统为例，通过MATLAB开展仿真，额定电压为12.66 kV，含有5个联络开关，编号为(33,34,35,36,37)，总负荷为(3 715+j2 300) kVA，基准功率为10 MVA。在改进算法中，设粒子数20、最大迭代次数tmax=30次、加速系数c1=c2=2.0、粒子的维数37、最大速度vmax=4、惯性权重wmax=0.95、wmin=0.4。

3.2 含单一分布式电源优化

接入单一分布式电源(PQ节点)，优化前后比较如表1所示，电压曲线如图1所示。

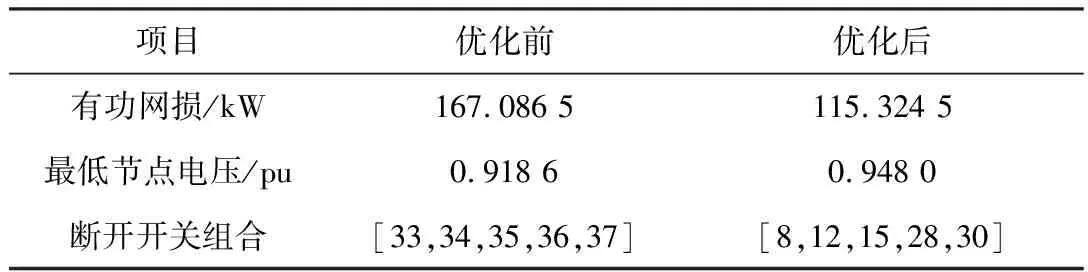
表1 单一分布式电源优化数据

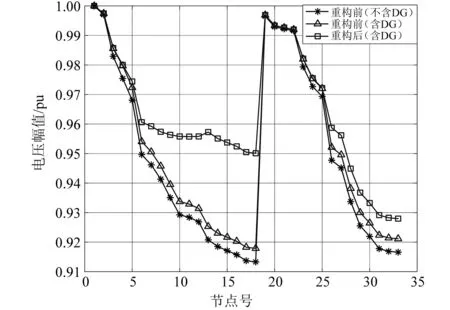
图1 含单一分布式电源优化前后电压曲线

如表1、图1可见，接入单一分布式电源后，优化后有功网损从167.086 5 kW降低到115.324 5 kW，比初始网损低了约30.97%，最低节点电压从0.918 6 pu增加到0.948 0 pu，增加了约3.2%。

3.3 含多种分布式电源优化

接入多种分布式电源进行仿真，优化前后的结果如表2所示，电压曲线变化如图2所示。由此可见，接入多种分布式电源后，初始网损降低到114.676 2 kW，最低节点电压提高到0.932 1 pu。利用算法优化后有功网损降低到了81.128 3 kW，最低节点电压提升到0.951 6 pu。可知，经过优化算法后，可以使有功网损大幅度降低，各节点电压水平有效提高。

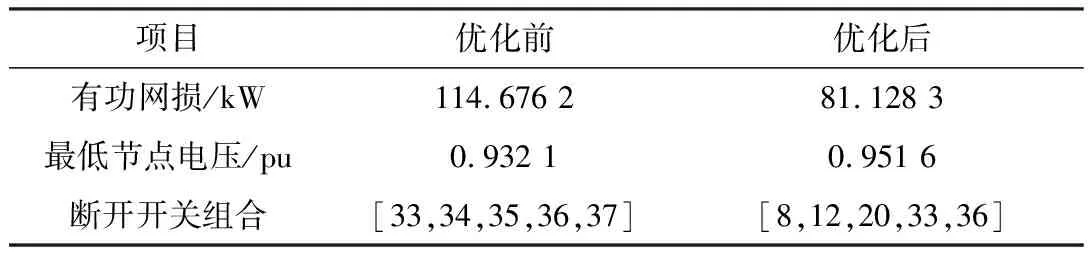
表2 多种分布式电源优化数据

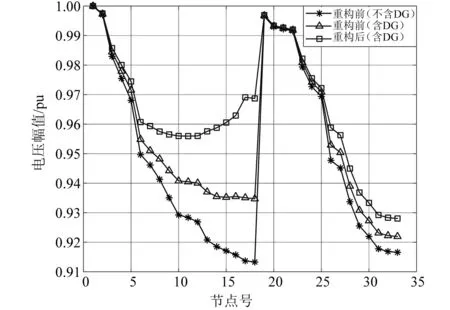
图2 含多类型分布式电源优化前后电压曲线

4 结束语

本文提出了一种基于改进二进制粒子群算法的含分布式电源的配电网运行方式优化方法。采用新的转换函数和具有变异操作的粒子位置更新方式来搜索最优方案，能有效降低配电网有功网损和提升节点电压水平，验证了改进算法在配电网优化中的可行性和优越性。研究成果对提升配电网供电可靠性和服务水平具有一定的理论价值。