基于自适应灰色分数加权模型的用电量预测研究
林琳, 高雪, 甄钊
(1.保定电力职业技术学院 国网冀北电力有限公司技能培训中心,河北 保定 071051;2.华北电力大学,河北 保定 071003)
0 引 言
许多研究表明,一个地区的用电量与它当地经济的发展密切相关,被称为“晴雨表”。电力作为最重要的二次能源,在终端能耗中占有较高的比例,考虑到电力资源的非储存性,供过于求会产生巨大的投资浪费和能源消耗,会对经济发展产生负面影响。因此,可靠的用电量预测对制订正确的能源发展规划至关重要。
由于用电量受各种不确定因素的影响,准确预测有一定难度。为了解决这一难题,人们采用了多种方法来建立预测模型,这些方法可以分为三种类型:时间序列方法、统计模型和机器学习方法[1-5]。时间序列模型是电力预测中最基本和应用最广泛的方法之一,它根据历史序列预测未来的趋势。当观测值数目足够大时,时间序列方法可以获得更高的预测精度,但是它们过于依赖过去的数据,缺乏可解释性。统计模型在可解释性、简单性和易于部署方面比其他模型更具优势。机器学习方法是处理用电问题的更为先进的方法,它们适用于更复杂的计算。其主要缺点在于其内部运行机制未知,只有在大数据的情况下,才能获得满意的预测精度,这就需要在数据编制上付出很大努力。文献[6]利用蚁群优化算法,开发了一种混合灰色方法来提高预测的鲁棒性和稳定性。文献[7]构建了一个由多个变量驱动的新颖的灰色模型来预测用电量。GM(1,1)模型是灰色预测方法的一个重要研究分支,通常以最后一次累积数据为初始条件,建立模型整合新数据,但是忽略了其他时间点对系统的影响,容易造成信息丢失[8]。
为了弥补这一不足,后续的研究加强了新的信息优先原则。从新的信息优先级的角度来看,新的发展趋势在预测不确定系统行为方面更具指示性。通过加强新信息对发展趋势的修正作用,提高了预测能力的准确性。分数阶累积算子通过增加对短期信息的权重,减少对长期信息的权重,可以有效提高灰色模型的建模精度。为了获得更准确的用电量预测,本文构造了动态分数阶加权系数来设计初始条件,通过粒子群优化计算自适应分数加权系数和对应时间参数,进一步提高了自适应能力和预测精度。
1 SFOGM(1,1)模型
GM(1,1)广泛应用于电力能源和高科技产业能源中[9],在GM(1,1)预测模型中,其初始条件对于预测精度起着至关重要的作用。尽管有学者做了一些修改初始条件的工作,但结果仍不理想。本文提出了一种新的分数加权初始条件,能适应多种特征的原始数据的模型,称为SFOGM(1,1)。
原始数据表示为:
X(0)={x(0)(1),x(0)(2),…,x(0)(n),n≥4}
(1)

因此,通过计算相邻累积值的平均值得出Z(1)={z(1)(2),z(1)(3),…,z(1)(n)},其中z(1)(k)=0.5z(1)(k-1)+0.5z(1)(k),k=2,3,…,n。
GM(1,1)模型的公式可以通过等式(2)表示。
x(0)(k)+az(1)(k)=b
(2)
式中:a为发展系数;b为灰色输入。其微分方程式表示为:
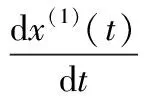
(3)
式中:x(1)(t)为1-AGO数据序列;t为数据的序列号;a和b为未知方程系数。设
(4)
式(4)中向量P的计算是求解灰色方程的关键。
本文通过引入动态可调分数加权系数对初始条件进行优化。然后提出了一种新的自适应分数加权灰色模型,简称SFOGM(1,1)。
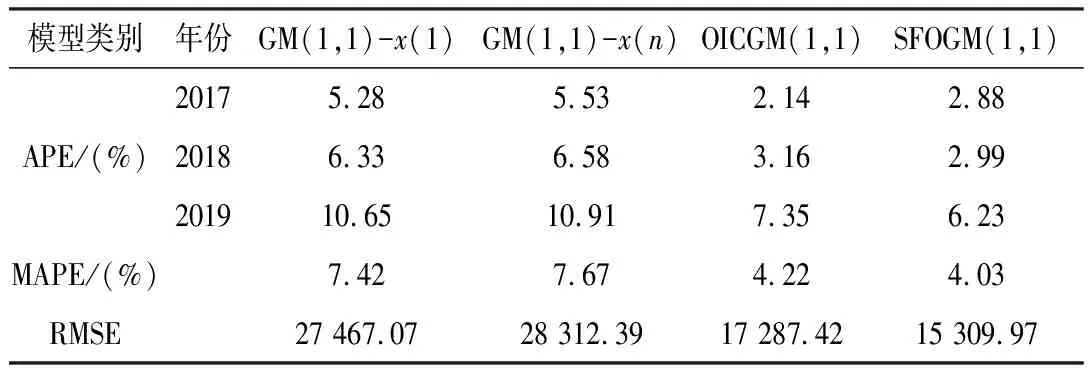
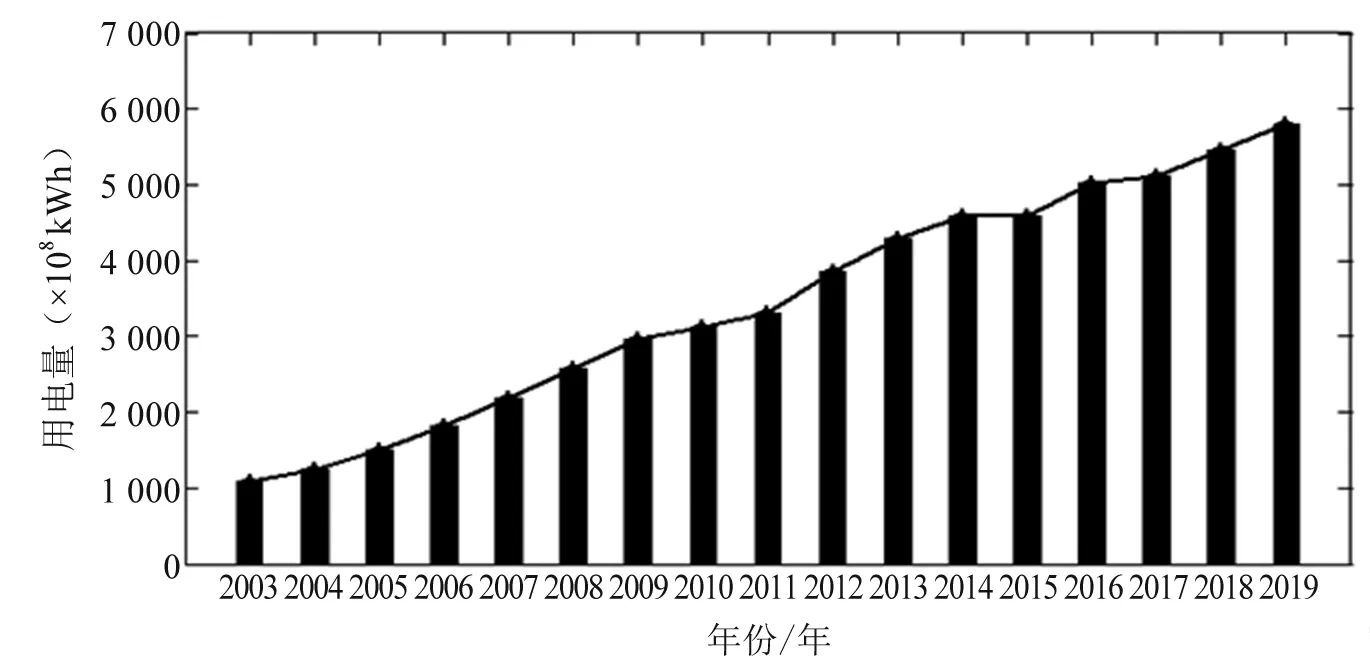
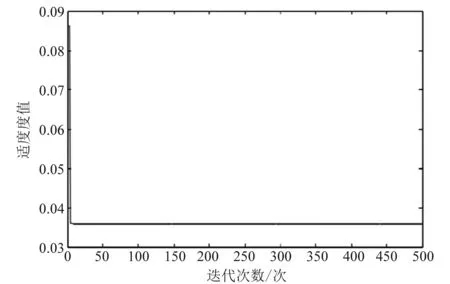
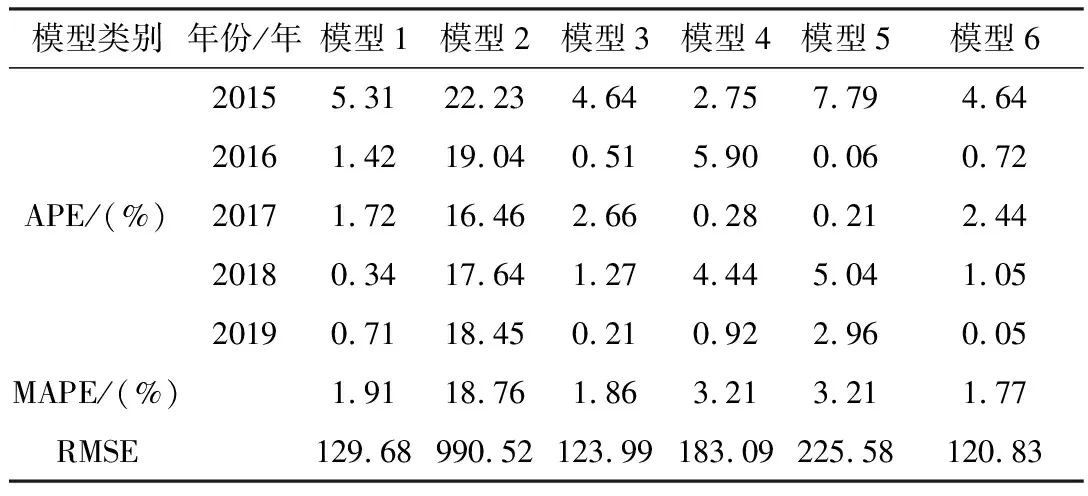
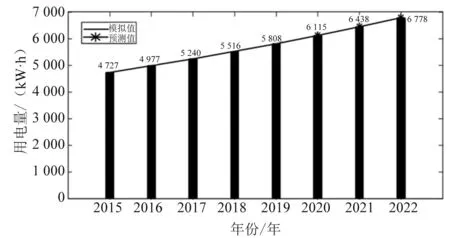
假设r(0 (5) 在βj的生成阶段,自适应分数参数r通过更新新旧信息的权值,灵活地拟合序列的变化趋势。由此,构造的初始条件为: x(1)(t0)=β1x(1)(1)+β2x(1)(2)+…+βnx(1)(n) (6) 式中:t0为输入时间参数;x(1)(t0)为其对应的初始条件。离散时间响应函数及公式如式(7)、式(8)所示。 (7) (8) 初始条件的参数采用粒子群优化算法(PSO)通过最小化仿真值与实际值之间的平均绝对百分比误差来确定[10]。PSO算法的主要步骤如下[11-13]。 首先定义向量[r,t0],建立适应度函数,然后初始化。M为粒子数,L为最大迭代次数,求最小值MAPE,得到适应度函数如式(9)所示。 (9) 式中:Q(i,j)为第i代第j个粒子的位置。计算每个粒子的适应度,确定全局最优粒子gbest和个体最优粒子pbest,在每一次迭代中,粒子通过跟踪这两个“极值”来更新自己,粒子通过下面的公式来更新自己的位置和速度,如式(10)所示。 Vk+1=c1(pbestk-xk)R1+c2(gbestk-xk)R2 (10) 式中:c1和c2为加速度因子;R1、R2为随机变量,R1、R2∈[0,1];粒子的位置通过Q(i,j+1)=Q(i,j)+vk进行更新。下一个粒子速度如式(11)所示。 Vk+1=wvk+c1(pbestk-xk)R1+c2(gbestk-xk)R2 (11) 式中:w为权值,可以从相应的gbest获得。 SFOGM(1,1)模型的建模具体流程如下,主要包括五个步骤。 (1) 得原始数据,计算中间变量的值。累积序列X(1)和背景值Z(1)是灰色模型的中间变量,通过使用这两个经过处理的序列,可以进一步削弱原始数据中隐藏的随机性,使灰色模型能够提高预测的精度。 (12) 其中: (13) (3) 通过求解式(2)当中的微分方程,构造优化的初始条件,得到预测函数。针对之前初始条件的不足,提出了一种新的具有灵活动态分数阶加权系数的初始条件,新的初始条件使新的数据点相对于旧的数据点具有更高的权重,使灰色模型能够提供更好的预测精度。 (4) 采用粒子群算法确定自适应分数参数r和时间参数t0,从而得到适应度函数。 通过对我国能源消费量的预测来论证新提出的模型SFOGM(1,1)和现有模型GM(1,1)-x(1)(1),GM(1,1)-x(n)(1),OICGM(1,1)的优势比较[14-15]。为了评估几种模型之间的预测性能差异,计算了三个精度指标,包括绝对百分比误差(APE),平均绝对百分比误差(MAPE)和均方根误差(RMSE)。 4种模型的预测精度如表1所示。3个精度指标表明新提出的模型整体效果最佳,由于以往的初始条件优化方法都在一定程度上增强了新信息的校正效果,需要进一步改进。而SFOGM(1,1)模型改变了原始时间参数和模型的累积顺序,因此提高了预测模型的灵活性。 表1 4种模型的APE、MAPE 和 RMSE 值 为了证明所建模型的有效性,利用SFOGM(1,1)对实际某省的用电量进行预测,某省的实际用电量如图1所示。通过与现有模型进行比较,验证了新提出模型的有效性。 通过与GM(1,1)-x(1)(1)、GM(1,1)-x(n)(1)、OICGM(1,1)、指数平滑法和自回归适应模型(即模型1、模型2、模型3、模型4和模型5)的比较,验证了SFOGM(1,1)模型(模型6)相对于现有模型的优势。这些竞争模型可以描述为两个不同的类别,即其他灰色模型(模型1、模型2和模型3)和非灰色时间序列模型(模型4和模型5)。通过对不同基准模型的比较,进一步验证了模型的有效性和适用性[14-15]。 图1 某省用电量数据统计 图2显示了该过程中最佳粒子轨迹位置。从每次迭代中的轨迹路径来看,可以看出PSO算法具有很好的收敛性,并且可以在100次迭代中快速获得最佳值。 为了比较,构建了5个模型作为基准模型,表2列出了2015年至2019年的预测结果。表3展示了由6个仿真模型确定的APE、MAPE和RMSE的值。图3显示了模拟的误差分布图。 图2 粒子群的轨迹过程 表2 6个仿真模型的预测值 表3 6个仿真模型的APE、MAPE和RMSE值 图3 模拟误差分布图 从表3可以看出,SFOGM(1,1)模型的MAPE为1.77%,而其他3个灰色模型的MAPE更大,分别达到1.91%,18.76%和1.86%。对于RMSE,SFOGM(1,1)模型的表现也更好,为120.83。其他3个灰色模型的RMSE为129.68,990.52,123.99。从这些对比数据中可以看出SFOGM(1,1)模型为最优模型,而OICGM(1,1)模型获得次优精度。 图3为模拟的误差曲线。从图3可以看出,优化后的SFOGM(1,1)模型效率最高,而GM(1,1)-x(1)(1)模型效率最低。与前3个模型不同的是,GM(1,1)-x(1)(1)模型是以第一个数据为初始条件建立的,对新信息利用较少,虽然简单的建模机理使得GM(1,1)模型得到了广泛的应用,但也应注意其存在的缺陷,难以为能源决策提供更准确的参考。综合来看,SFOGM(1,1)模型在用电量预测中表现出了良好的性能,它能更好地利用所有数据信息。 利用式(8)介绍的SFOGM(1,1)模型,得出某省2020—2022年用电量预测值,如图4所示。从图4可以看出,该省的电力消费预计将保持可持续增长。预计2022年达到6 778 亿kW·h时,增速将放缓,从2019年的6.39%降至2022年的5.28%。原因主要有两个方面:一方面,节能技术得到了广泛推广;另一方面,随着环保意识的增强,人们的用电量减少。 图4 某省用电量发展趋势 电力消费的准确预测一直对能源计划和经济发展有很大的影响。因此,提出一种适合短期预测的方法是很有意义的。首先,在新信息优先级的基础上,设计了灵活动态的分数阶加权系数来构造新的初始条件;其次,建立了自适应分数加权灰色模型。而新提出的SFOGM(1,1)模型可以更好地利用时间序列中最近隐藏的信息,而没有足够的数据;此外,利用粒子群算法估计自适应分数加权系数和时间参数;再次,运用自适应分数加权灰色模型研究江苏省用电量的发展趋势;最后,还预测了到2022年的潜在发展趋势。现有的研究虽然在一定程度上提高了预测性能,但由于严格依赖数据的数量和质量,其对各种情况的适应能力仍受到一些限制,今后将进一步深入研究。
2 求解参数的初始条件
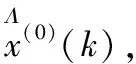
3 仿真分析


4 结束语

