“通信原理”中采样与信道容量的直观教学

林巍峣 刘士湛

(上海交通大学 电子信息与电气工程学院， 上海 200240)

奈奎斯特采样定理和有噪信道编码定理是“通信原理”课程中的两个重要定理，由于分别在信道最大符号传输速率的确定与信道容量的计算中发挥重要作用，因而一直是教学重点[1]。

为了方便教学，教师们已经提出了多种多样的教学方法。针对奈奎斯特采样定理，文献[2]提出结合压缩感知对采样定理进行教学，可以看作对采样定理的前沿拓展；文献[3]认为需要调整教学顺序，首先教授离散傅里叶变换(DTFT)，再采用以问题为导向的方式进行教学；文献[4]则强调采用问题牵引式的教学模式，将授课内容分为问题、模型、方法、原理和应用五个阶段，并主要在频域解释定理内容。另一方面，针对有噪信道编码定理中的信道容量，文献[5]和[6]将信道容量类比为道路所能承载的最大车流量，带宽类比为道路宽度，信噪比类比为行车秩序来进行解释；文献[7]则主要通过随堂测验来强化学生的计算能力。

然而，两个定理各自蕴涵的事实与初学者的直觉往往相悖，而现有教学方法很少针对这些地方进行解释。对奈奎斯特采样定理而言，初学者难以理解为什么以一定采样率对带限的连续信号采样，得到的离散序列能够完全重建出原始信号。而现有的教学方法以公式推导为主，很少直观回答这一问题；对有噪信道编码定理而言，学生则对“存在噪声的情况下信息不能以任意低的错误率无限快地传输”抱有疑惑，现有的教学方法也鲜有此问题的直接解答。因此，直接对学生容易产生的疑惑进行解释，并设计了简单的验证实验，以供教学时参考。

1 采样定理

1.1 定理内容

奈奎斯特采样定理是理想低通信道中最高码元传输速率的公式，在连续时间信号和离散时间信号之间架起了桥梁，内容包括时域采样定理和频域采样定理。由于二者的结论和推导类似，教学中一般以时域采样定理为教学重点，其内容如下：

对于有限带宽的连续信号x(t)，假设其频谱的最高截止频率为fm，以fs的采样频率对其进行采样得到x[n]，当采样频率fs≥2fm时，可以由x[n]恢复出x(t)。

时域采样定理的教学通常以公式推导和频域分析为主。采样可以看作是时域上均匀分布的冲激序列与原始信号相乘的过程，写作：

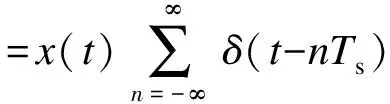
(1)

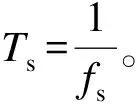
(2)

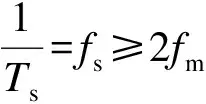
1.2 主要疑问与直观理解

1.1节中的推导教学为学生提供了对采样定理频域作用的理解，但初学者往往会产生如图1所示的疑问：采样得到的离散点之间存在很多种连接方式，重建时为何能唯一恢复出原始信号？图1中，黑色点为离散的采样点，而三条不同线形的曲线都能够穿过所有采样点。

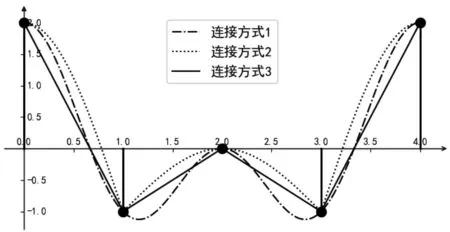
图1 离散点之间存在多种连接方式

下面从频域直观地解答这一疑惑，强调带宽限制是唯一恢复原始信号的关键。图2中画出了三种连接方式分别对应的频谱，其中两条虚线分别在频率为-0.5 Hz与0.5 Hz的位置，而两条实线分别在频率为-7.5 Hz与7.5 Hz的位置。可以观察到，连接方式1的频谱是带限的，且位于两条虚线之间；而连接方式2和3的频谱都无限延展，在实线处幅值才基本为零。

考虑到离散点的采样率为fs=1 Hz，按照采样定理，连续信号的频率需要在0.5 Hz以内。因此，正确的连接方式仅有一种，可以依据采样得到的离散点唯一恢复出原始信号。

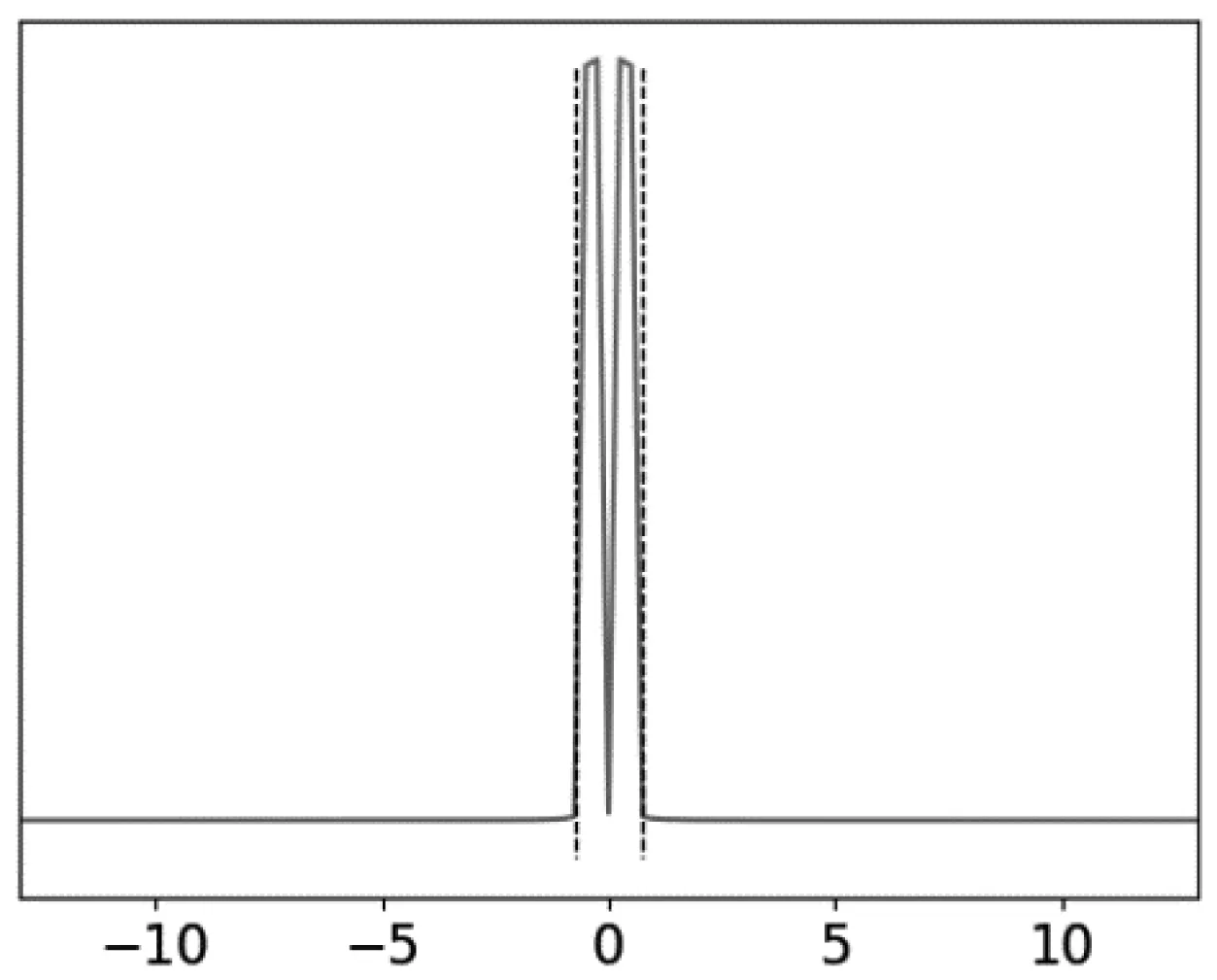
(a) 连接方式1的频谱

(b) 连接方式2的频谱

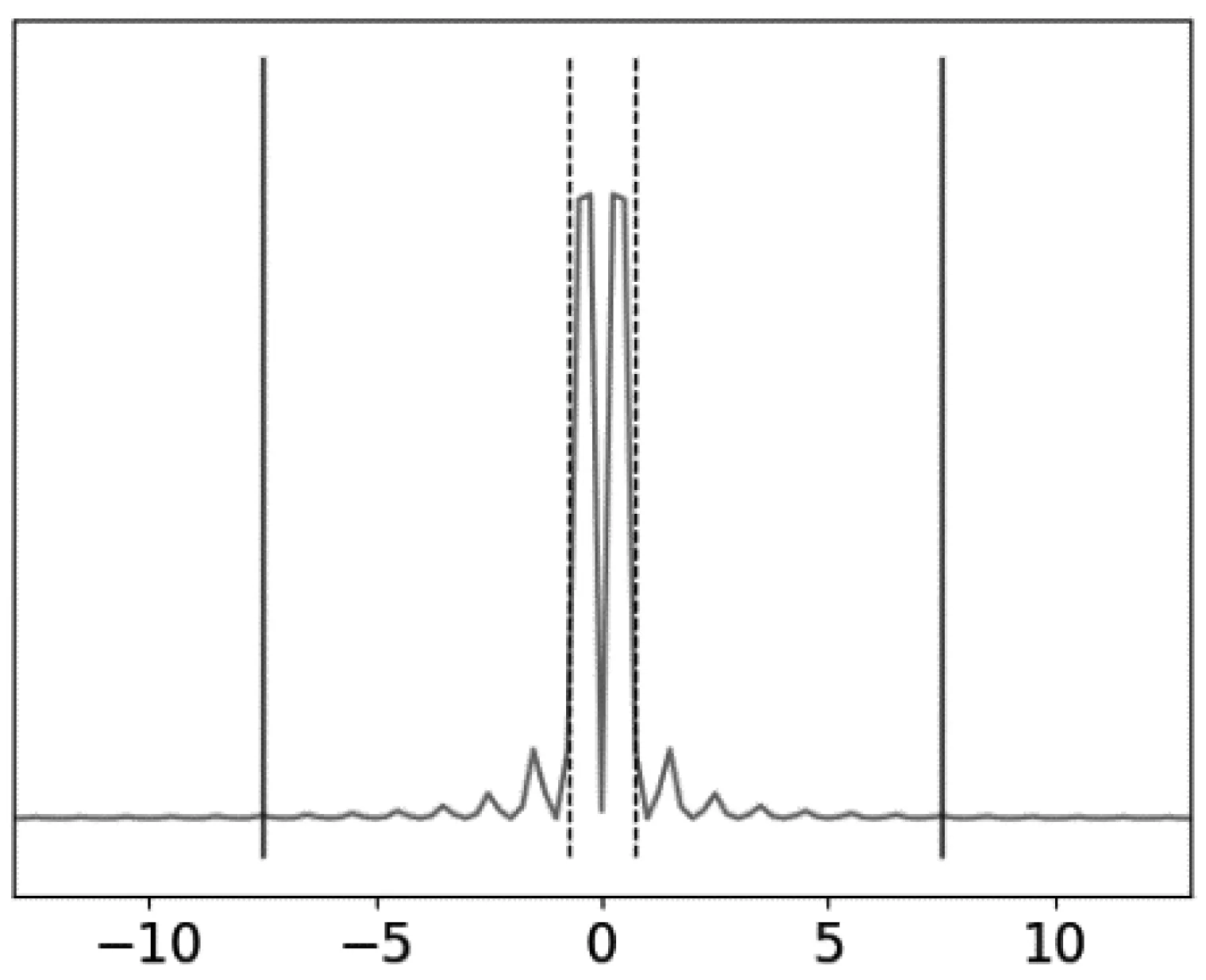
(c) 连接方式3的频谱

(d) 连接方式3的采样图2 不同连接方式对应频谱

对于带宽更大的连接方式2与3，依照采样定理，至少需要fs=15 Hz的采样率才能损失较小地恢复出原始信号，如图2(d)所示。

1.3 实验设计

为了促进学生对定理内容的理解，同时设计了以下实验来验证采样定理。

考虑余弦信号x(t)=cos(πt)，分别使用fs1=1和fs2=0.25的频率对x(t)进行采样，对应图3中的圆形采样点和方形采样点。x(t)的频率小于等于1/2，因此fs1=1恰好满足采样定理的条件，而fs2不满足。

等价地，可在已知x(t)是余弦信号且周期大于等于2的情况下，分析两种采样方式各自能否重建出x(t)。由图3可知，当且仅当x(t)=cos(πt)时，曲线能够穿过以采样率fs1采样得到的所有点。而以采样率fs2采样得到的点还可以被曲线x′(t)=cos(0.5πt)穿过。

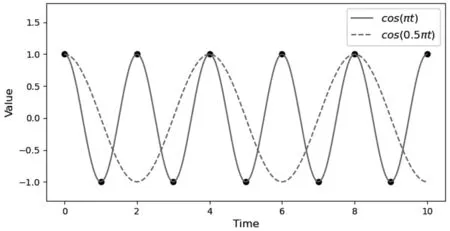
(a) 以fs1=1的采样率采样

由于傅里叶变换相当于将信号x(t)投影在不同周期的正弦和余弦函数上，因此上述对余弦信号的分析是可以推广到其它带限的连续信号上的。

2 有噪信道编码定理

2.1 定理内容

有噪信道编码定理是香农(Shannon)1948年证明的关于信息最大传输速率的定理，即将信息以任意小的错误率传输通过信道的速率是存在上界的，该上界被称为信道容量。当信源的熵率大于该信道的信道容量时，信息将不能可靠地传输。对于连续时间下带宽有限的加性高斯白噪声(AWGN)信道，其信道容量为：

(3)

(a) 噪声

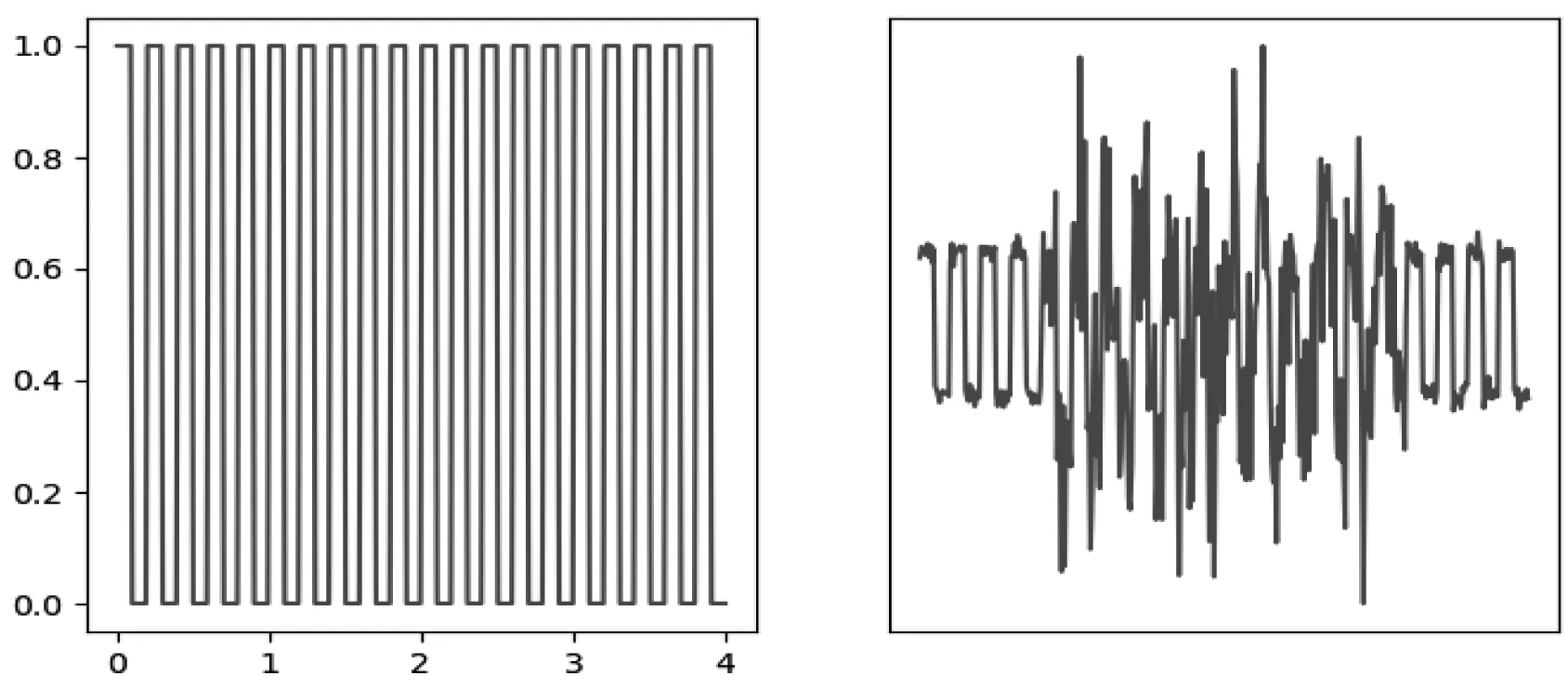
(b) 传输速率快

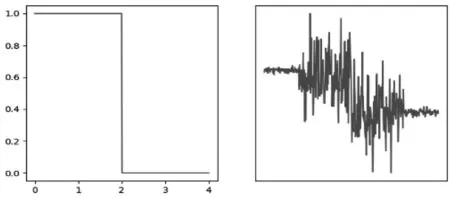
(c) 传输速率慢图4 噪声对不同传输速率信号的影响

有噪信道编码定理的教学通常以公式推导和概念讲解为主。首先讲解熵率、互信息和信道容量的定义，然后推导得到离散时间AWGN信道的信道容量。结合采样定理，就能得出式(3)的结果。

2.2 主要疑问与直观理解

2.1节的推导较为抽象，初学者往往难以领会香农公式的核心思想，产生下列疑问：噪声独立地作用在各个时刻，为什么在较低的传输速率下，信号可以以任意低的错误率传输？噪声为什么限制的并非误码率，而是最大信息传输速率？

以方波信号为例，直观地分析噪声给不同传输速率的信号带来的影响，如图4所示。不妨假设噪声在一段时间内特别大，而其它时间很小。图4(b)中以较快的速率传输信号时，噪声较大部分的信号受到严重干扰，难以鲁棒传输；而以较慢的速率传输信号时，即使部分信号被严重干扰，接受端仍能通过噪声较小的信号恢复出对应信息。

由此可见，较低的传输速率使得信号中有较大的冗余性，接收端可以通过滑动平均等方式恢复出信息，从而实现较低的错误率。因此，噪声对误码率的影响可以转化为对最大传输速率的限制，在噪声存在时信号不能以极低的错误率无限快地传输。

2.3 实验设计

为了帮助学生更好地理解有噪信道编码定理，设计了如下实验，验证同一信噪比下不同传输速率给误码率带来的影响。

图5中展示了信号功率是噪声功率三倍的情况下，不同频率的方波信号的传输结果。图6(a)中的方波信号频率为0.5 Hz，(b)中信号的频率为2 Hz，两种情况的采样率相同，因此后者在相同时间内携带的信息量是前者的四倍。图5图中从左到右依次是：原始信号、噪声、滑动平均并进行判决后的信号。可以观察到，频率为0.5 Hz的信号经过滑动平均和判决后，基本上能够重建出原始波形；而频率为2 Hz的信号则存在明显的误码。

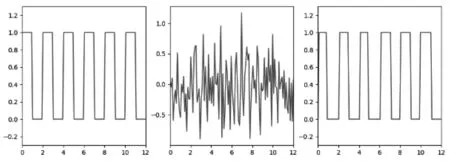
(a)低传输速率

(b)高传输速率图5 从左到右依次为：原始信号、噪声、滑动平均并判决后得到的信号

由此可见，在相同的信噪比下，信号传输速率不能无限提升，过大的传输速率会导致接收端误码率增大。

3 结语

阐述了“通信原理”课程中对采样定理和信道容量的直观理解。其中，针对采样定理中“将带限连续信号按照一定采样率采样为离散信号后，可以无损重建出原始信号”的结论，分析了离散点的不同连接方式，指出满足奈奎斯特带宽限制的连接方式是唯一的。针对有噪信道编码定理中“信息不能以任意低的错误率无限快地传输”的结论，直观展示了噪声给不同传输速率的信号带来的影响。由于两个定理的结论都与初学者的直觉有一定出入，因此这种直观的理解对教学有一定指导作用。调研了某两年学生对采样定理和信道容量所在章节的教学满意度反馈，如图6所示，可以看到在使用直观教学方法后，学生对课程重难点讲授的满意度有了明显改善。

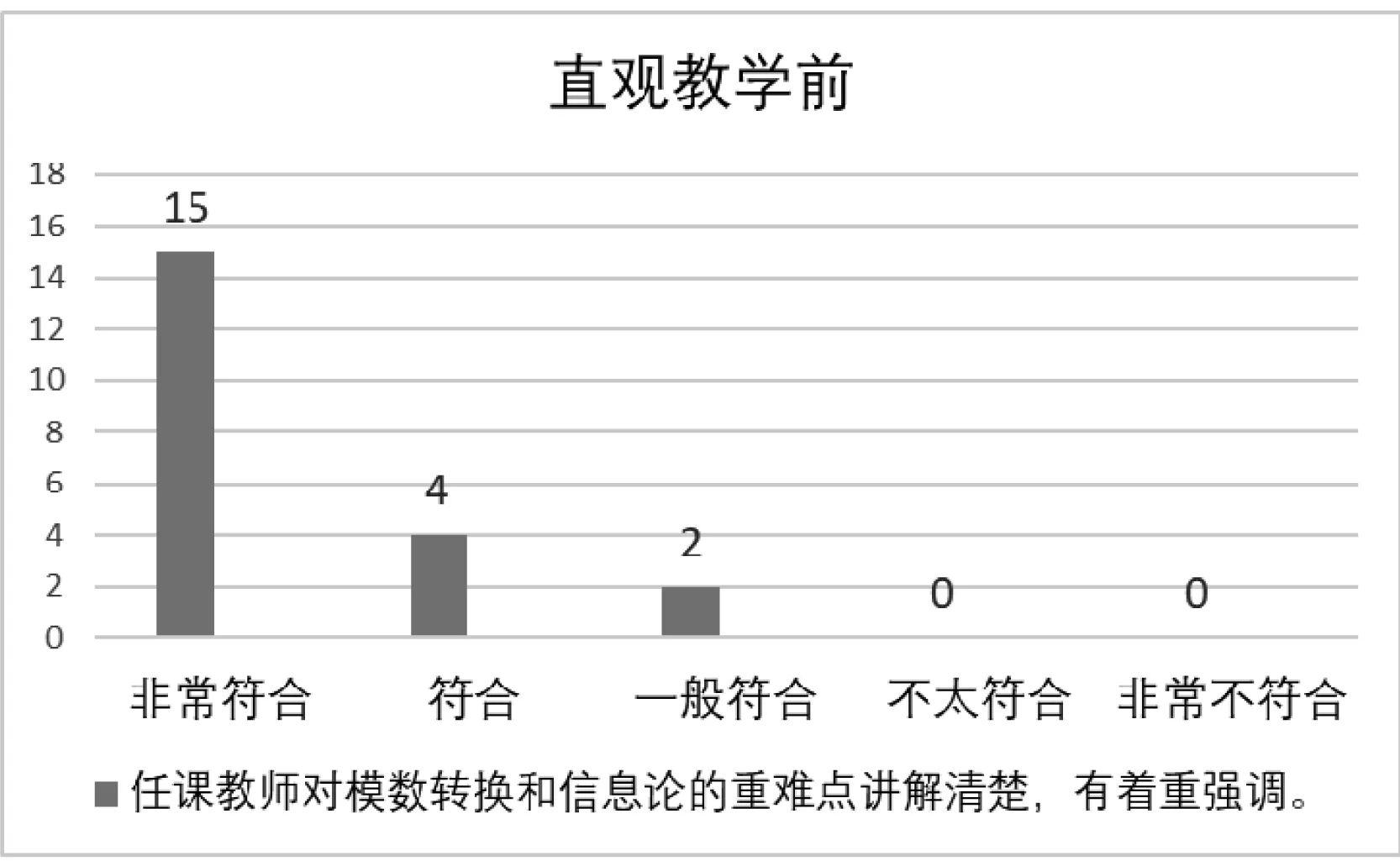
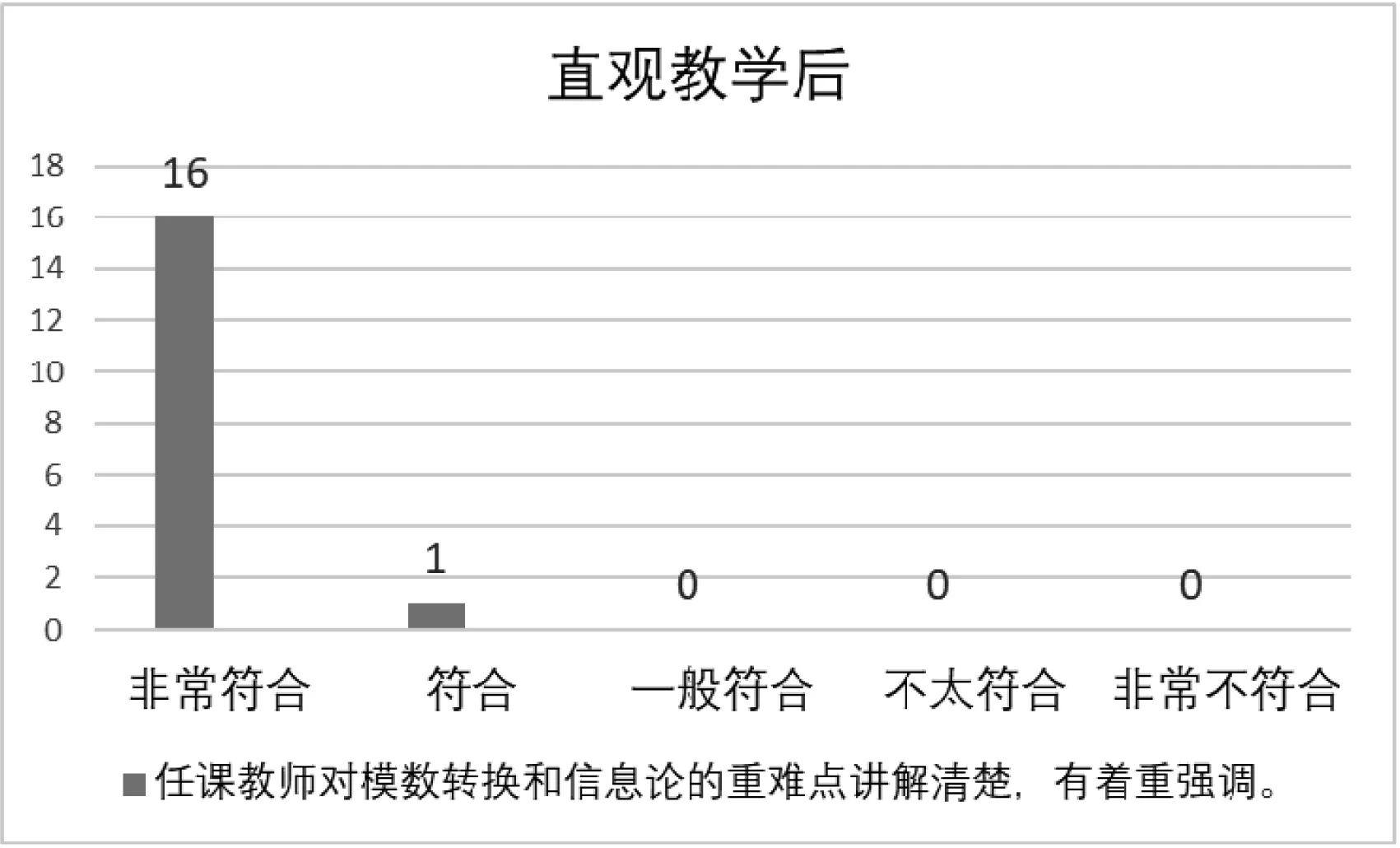
图6 直观教学效果