基于GOOSE通信的风电场快速调压控制策略研究
郭春岭,蔡国洋,单馨,牛超
(1.南瑞集团有限公司(国网电力科学研究院有限公司),江苏 南京 211000;2.国电南瑞科技股份有限公司,江苏 南京 211000)
0 引言
随着“双碳”目标和构建以新能源为主体的新型电力系统目标的提出,高比例新能源的电力系统快速从局部向全国发展。新能源发电在电压、频率和阻尼等方面的局限性逐步呈现,大电网的安全稳定运行面临巨大挑战。
电压支撑强度和频率支撑强度是表征电力系统强弱的两个主要特性[1],但风力发电、光伏发电均采用电力电子变换器作为和电网的接口,其运行特性不同于常规同步机组,主要表现为等效转动惯量小、一次调频能力不足、电压调节能力有限等。随着电力系统电力电子化程度不断提高,系统稳定性由同步机主导逐渐过渡为由电力电子设备主导,导致电网抗扰动能力下降,且易引发连锁故障和次同步振荡[1-5]。在新能源高渗透率场景下,利用风电、光伏的无功余量对系统电压水平进行优化,提高系统电压水平[6],是解决这一问题的重要途经之一。
因此,针对新能源发电技术,不仅要研究如何更好地参与电力系统的调峰控制和稳态控制,更要研究如何改善动态和暂态性能,能够提供接近或高于常规电源对系统功角、电压、频率的动态支撑能力,同时提高抗干扰能力。
目前很多学者从单机、风电场、风电场群等多个空间尺度上对风力发电的电压无功支撑进行了研究。针对单台风电机组的电压无功支撑能力,除了故障穿越技术的研究[7-8]外,研究主要集中在无功支撑能力的评估[9-12]上。在风电场无功电压控制方面,文献[13]提出一种计及机组电压无功相关性的风电场层无功电压控制,可以减少各机组机端电压的差异;文献[14]提出一种基于模型预测控制的双馈风电场无功电压控制策略,可有效降低风速快速波动对风电场无功快速调节能力的影响;文献[15-17]结合新能源发电单元和静止无功发生器(static var generator,SVG),从不同角度研究了二者同时参与新能源电站无功电压控制的策略。在风电场群这个层级,文献[18]提出了一种综合考虑静态电压稳定裕度、汇集系统电压均衡和动态设备无功裕度的风电汇集系统无功电压协调控制策略,来改善风电汇集系统的静态电压稳定性。文献[19]则针对大规模风电集中并网的场景,提出了一种自律协同的电压控制架构,利用自律控制和协同控制平抑电压的快速波动。
上述研究中,关于单台风机无功电压支撑的研究未涉及多台风机之间的协调,关于风电场无功电压支撑方面的研究或者未有效考虑风机的动态无功支撑能力,或者未考虑无功电压支撑的快速性等,而风电场群的无功电压支撑研究最终是要以风电场具备高效可靠的无功电压支撑能力作为基础的。因此有必要深入研究如何实现风电场对电网快速、高效的无功电压主动支撑。
本文提出一种基于高速通用面向对象变电站事件(generic object oriented substation event,GOOSE)通信的风电场快速调压控制方法及系统,通过采集风电场并网点电压、无功值和计算系统阻抗,来计算获取电压波动时所需的无功功率目标值;通过获取每台机组的无功裕度来实现对风电场所需无功功率目标值的第一轮等裕量无功预分配,再计及阻抗矩阵和潮流约束进行第二轮无功分配算法优化。最后,进行了试验验证,本文提出的方法能实现高效、快速的无功电压支撑,响应时间达到50 ms,证明了通过充分挖掘风电机组的能力,风电场可以提供快速的无功电压支撑。
1 风电机组无功电压支撑能力分析
以双馈风力发电机组为例分析其无功电压支撑能力。双馈风机的定子直接接入电网,转子通过一个背靠背的电压型脉宽调制(pulse width modulation,PWM)变流器接入电网,实现对有功无功的解耦控制。双馈感应风机的无功功率由定子侧无功功率和网侧变换器无功功率两部分组成,即:

式中,Qg为双馈感应风机的总无功功率;Qs为定子侧无功功率;Qc为网侧变换器无功功率。
在已知定子端输出有功功率Ps的情况下,Qs要受到定转子电流的约束极限,其中转子电流为主要制约因素,Irmax为转子最大电流,约为1.2倍额定转子电流;Ismax为定子最大电流。定子侧有:
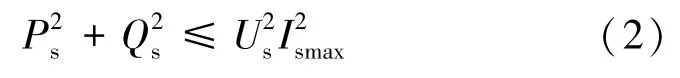
式中,Us为定子侧电压。
dq坐标系下,双馈感应风机的电压方程和磁链方程如下:

式中,usd、usq分别为定子电压的d、q轴分量;urd、urq分别为转子电压的d、q轴分量;isd、isq分别为定子电流的d、q轴分量;ird、irq分别为转子电流的d、q轴分量;Rs、Rr分别为定子和转子绕组相电阻;ψsd、ψsq分别为定子磁链的d、q轴分量;ψrd、ψrq分别为转子磁链的d、q轴分量;ω1为同步角速度;ωslip为转差角速度;Ls为定子电感;Lr为转子电感;Lm为激磁电感。
采用定子电压矢量定向的同步dq坐标变换,即将同步旋转dq坐标系的d轴和定子电压合成矢量Us同向,则有:

式中,Us为定子电压的峰值,风机并网之后为电网电压,视作恒定值。
进一步计算可得双馈电机定子端发出的有功功率和无功功率为:

可见,分别控制定子dq轴电流isd、isq可以控制输出的有功和无功功率,实现风机的有功功率和无功功率的解耦。
忽略定子电阻压降,稳态时定子合成磁链落后于定子电压矢量Us90°且恒为定值,在定子电压矢量定向同步dq坐标系下,可得:

式中,ψs为定子总磁链。
由式(4)、式(6)和式(7)计算可得,转子电流分量和定子端输出有功功率和无功功率存下以下关系:

对转子侧电流,有:

代入可得:

式中,Irmax为转子最大电流,一般取1.2倍转子额定电流。
将式(10)进一步推导可得:

式中,Xs为定子电抗且Xs=Lsω1;Xm为励磁阻抗且
Xm=Lmω1。
由式(11)计算可得定子端输出无功功率的范围为:

式中,

网侧变换器的无功容量受到有功出力和自身容量的约束。根据双馈风电机组的内部功率关系,记s为双馈电机的转差率,则网侧变换器的有功出力为Pc=sPs/1-s( )。根据以上功率关系,设网侧变换器容量为Sc,整理可得网侧变换器的无功范围为:

式中,

定子侧无功功率和网侧变换器无功功率的和为双馈机组无功能力范围,即最小无功Qgmin和最大无功Qgmax分别为:

2 风电场快速调压控制策略
受电力系统扰动影响,根据系统无功电压下垂特性,当风电场并网点电压的变化偏离合理范围时,需要提供快速的无功支撑,将风电场电压恢复到合理范围,平衡系统的扰动,本文提出策略的实现流程如图1所示。首先结合电压波动情况以及系统阻抗等计算需要快速提供的无功功率支撑;然后结合风电机组的无功支撑裕度、场站内阻抗矩阵及其带来的无功损耗等因素计算每台风电机组的无功功率目标值。

图1 风电场快速调压控制流程
2.1 风电场无功电压下垂特性
如图2所示为风电场无功电压下垂特性曲线。

图2 风电场无功电压下垂特性曲线
根据电压控制范围,下垂特性曲线分为三个区域。
1)当风电场并网点电压在电压控制死区(Ud-,Ud+)内时,不会进入快压控制区域。
2)当电压下降到Ud-以下时,风电场应根据上述曲线来增加无功输出,调压系数为k1,上限为风电场发出无功支撑能力上限。
3)当电压上升到Ud+以上时,风电场应根据上述曲线来减小无功输出,调压系数为k2,上限为风电场发出无功支撑能力下限。
2.2 总无功需求计算
风电场接入电网后的电压支撑强度可以通过系统短路容量和设备额定容量的比值,即短路比SCR来衡量:

式中,Sac为交流系统短路容量;PN为设备容量;Xpu为阻抗标幺值。
短路比表示系统对有功、无功功率的注入、吸收的响应能力,短路比大,表明系统对有功、无功功率注入、吸收的响应小,当电力电子设备功率变化时,系统电压不会受到显著影响。短路比小,表明系统对有功、无功功率注入、吸收非常敏感,系统电压随着注入、吸收的无功功率变化而迅速变化[1]。因此短路比,即等效系统阻抗是电压波动时计算无功需求量的重要元素。
为简化控制策略,采用在线辨识的方法获取等效阻抗,进而获取系统短路比,利用过去一段时间的无功、电压采样数据来计算等效阻抗,计算公式如下:

式中,Qt、Ut分别为t时刻的并网点无功功率和并网点电压;Qt-k、Ut-k分别为过去某个时刻的并网点无功功率和并网点电压;X为系统等效阻抗。
根据SCR计算,设无穷大电网电压为,则有:

式中,Pt为t时刻并网点有功功率;R为等效电阻。
进行无功补偿后,电压为:

式中,Pt+1、Qt+1、Ut+1分别为t+1时刻并网点有功功率、无功功率、电压;Ut∞+1为t+1时刻无穷大电网电压。
假设风电场无功补偿对无穷大电网的影响可以忽略,同时忽略电站有功的变化,则有且Pt=Pt+1,上述两式相减,可得:
进而求得无功功率需补偿:

无功功率需求增量ΔQref为:

2.3 风机无功分配
根据每台机组的无功裕度以及所需的无功功率目标值进行第一轮等裕量无功预分配,再计及阻抗矩阵和潮流约束对剩余的无功功率目标值进行第二轮无功分配算法优化,得出新能源场站每台机组所分配到的无功变化量指令值。
2.3.1 第一轮分配
根据每台机组实时更新的无功裕度,按无功极限比例进行第一轮无功分配,得到预估的无功功率分配初值为:

式中,ki为第i台机组的剩余无功功率极限比例;ΔQiref1、Qimax、Qi分别为第i台机组的无功功率第一轮分配初值、无功功率极限值、实测无功功率;ΔQref为风电场控制环节输出的实时无功功率需求增量。
2.3.2 第二轮分配
计算全场新增无功的无功损耗,表示为:

式中,

式中,ΔQloss为场站主动无功支撑带来的无功损耗;为无功支撑后的全场无功损耗;为无功支撑前的全场无功损耗;、、为无功支撑后的并网点高压侧有功功率、无功功率、电压;、、为无功支撑前的并网点高压侧有功功率、无功功率、电压;Xfarm为等效的场站阻抗。
根据各节点有功功率及无功功率求得预估的无功支撑后的节点电流,并根据新能源场站拓扑结构等效每个节点到并网点高压侧的阻抗,得到第i台机组的支撑无功损耗为:

式中,为无功支撑后的第i台机组电流;It i为无功支撑前的第i台机组电流;Xi为第i台机组到并网点高压侧的阻抗。
计及阻抗矩阵的无功损耗进行全场无功重新分配,表示为:

式中,ΔQi为潮流约束后的第i台机组的无功支撑变化量;ΔQiloss为第i台机组承担的无功损耗;ΔQloss为全场的无功损耗;Ki为第i台机组的裕度系数;ΔQiref2是新能源场站第i台机组第二轮分配到的无功增量。
3 试验方案
本文提出的控制策略在某风电场进行了试验,试验风电场设计安装30台单机容量为2.5 MW和14台单机容量为3.2 MW的风力发电机组,装机规模为120 MW,配套一座110 kV升压站,试验拓扑图如图3所示。

图3 试验拓扑图
3.1 电网信息采集
调压控制器直接接入并网点的TV、TA,采集并网点母线电压、有功功率、无功功率等电网信息。
3.2 与AVC子站协调
为避免试验过程中AVC子站控制对试验的影响,调压控制器与AVC保持通信,实现指令协调,即:并网点电压波动在快速调压控制死区内时,由AVC控制全场无功;当并网点电压波动超过快速调压控制死区时,调压控制器发闭锁指令至AVC子站,由调压控制器来控制全场无功。
3.3 与风电机组快速通信
GOOSE是IEC61850中的一种快速报文传输机制,基于4层通信协议栈,只用了国际标准化组织开放系统互联(ISO/OSI)中的4层(物理层、数据链路层、表示层和应用层),在数据链路层采用IEEE802.1Q协议,保证GOOSE报文的优先传送,从而提高了通信传输的可靠性和低延时。
基于GOOSE通信协议的以上特点,调压控制器与风电机组的变流器通过GOOSE建立通信,以保证通信可靠性和低延时。
3.4 工况模拟
从电压扰动模拟器向调压控制器的交流量中采集测试通道注入模拟电压阶跃扰动信号,观察全场无功功率和母线电压的变化。若注入的模拟电压信号为向下阶跃扰动,则母线电压应快速上升,上升值应接近模拟电压扰动的幅度;反之则母线电压应快速下降,下降值应接近模拟电压扰动的幅度。
4 试验结果及分析
4.1 模拟电压下阶跃
图4为模拟系统电压持续1 s的1 kV下阶跃时的母线电压、实际无功和目标无功曲线,其中目标无功为无功增量指令。

图4 模拟系统电压1 kV下阶跃
阶跃启动时刻为t=2 s,调压控制器向上调节无功功率。模拟阶跃开始前,即t=2 s时刻,系统电压118.91 kV,系统无功-4 759 kvar,无功指令为0;阶跃开始后10 ms,即t=2.01 s时刻,无功指令为4 457 kvar;阶跃开始后40 ms,即t=2.04 s时刻,无功增量指令为4 491 kvar,系统无功-1 012 kvar,系统无功增加3 747 kvar,系统电压119.64 kV,系统电压上升0.73 kV。
可以看出,当模拟电压向下阶跃1 kV开始后,控制系统能够在10 ms内完成无功目标值的计算与下发,系统电压能够在50 ms内快速上升恢复。
4.2 模拟电压上阶跃
模拟系统电压持续1 s的1 kV上阶跃时的母线电压、实际无功和目标无功曲线如图5所示,其中目标无功为无功增量指令。

图5 模拟系统电压1 kV上阶跃
模拟母线电压向上阶跃1 kV的启动时刻为t=2 s,调压控制器向上调节无功功率。模拟阶跃开始前,即t=2 s时刻,系统电压118.96 kV,系统无功3 428 kvar,无功指令为0;阶跃开始后10 ms,即t=2.01 s时刻,无功增量指令为-4 527 kvar;阶跃开始后40 ms,即t=2.04 s时刻,无功指令为4 496 kvar,系统无功-291 kvar,系统无功减 少3 719 kvar,系统电压118.10 kV,系统电压变化量0.86 kV。
可以看出,当模拟电压向上阶跃1 kV开始后,控制系统能够在10 ms内完成无功目标值的计算与下发,系统电压能够在50 ms内快速下降恢复。
5 结语
随着新能源占比的不断提高,电压失稳的风险越来越大,严重影响电网的安全运行,充分挖掘新能源发电单元的动态无功支撑能力,使其具备参与电网快速电压支撑的能力,是提升电网电压稳定的一个重要方法。本文首先分析了风电机组的无功电压支撑能力,并提出了基于电压下垂特性和系统阻抗的总无功需求计算方法,提出了基于风电机组无功支撑裕度和场内阻抗矩阵的风电机组无功分配策略;然后制定了引入GOOSE快速通信的试验方案,并进行了现场试验。试验结果表明,本文提出的策略在电压扰动发生时,能够快速地提供无功电压支撑,响应时间可以缩短到50 ms以内,验证了本文提出策略的有效性。
本文验证了风电场利用风电机组实现快速调压的可行性,后续研究将进一步完善控制策略,提升电压控制精度,研究如何才能更有效地利用风电场的这一快速调压能力来保障电网稳定的策略,及更具可推广性的应用方法。

