基于MATLAB的“四心法”椭圆画法及其偏差分析

闫培泽

（濮阳职业技术学院 机电与汽车工程学院，河南 濮阳 457000）

椭圆是工程上及生活中一种常见的图形，《机械制图》教材中讲解的常用椭圆画法有两种：同心圆法和“四心圆”法。很显然，同心圆法从理论上就确定了它画法的严谨性，在画图无误差的情况下，画出的就是一个标准椭圆。但凡事都有两面性，实际操作起来，因为需要描点并平滑连接，这种方法就显得比较繁琐。方便快捷的“四心法”画椭圆的方法就应运而生了。工程上更多的是“四心法”画图，快速高效，四段圆弧光滑连接，图形饱满[1]59。

一、“四心法”简介

（一）“四心法”画近似椭圆步骤

已知：长轴AB，短轴CD，作图（如图1）。

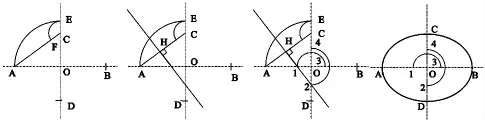
图1 “四心法”椭圆画法步骤

a.连接AC，画弧使OE=OA、CF=CE，求出点E、F；

b.作线段AF的垂直平分线，垂足记为H，交轴线于1、2两点；对称求出3、4两点；

c.分别用1、2、3、4点当圆心，把四条连心线作为分界线，过四点A、B、C、D分别作四段圆弧[2]26。

（二）“四心法”画椭圆的理论依据

这种椭圆画法的本质就是四段圆弧顺次连接组成一个椭圆的类似型，因此这是一种近似画法，以图1所示AC段椭圆弧为例，从圆弧连接的角度来看，它就是半径为1A和半径为2C的两段圆弧在直线12上内切连接而成。

在△A1H和△2HC中，A1对H1的差值应该等于2C对2H的差值。

为了叙述方便可以设∠HA1=∠H2C=α，AC=c，AO=a，OC=b。

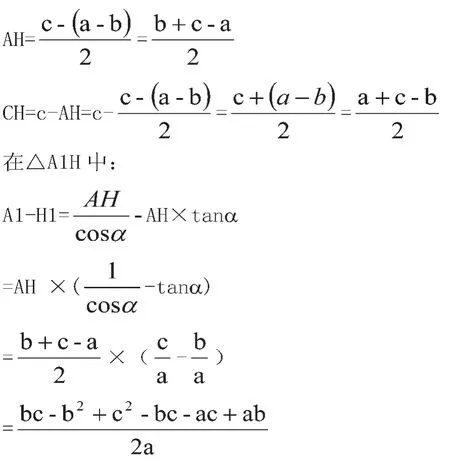
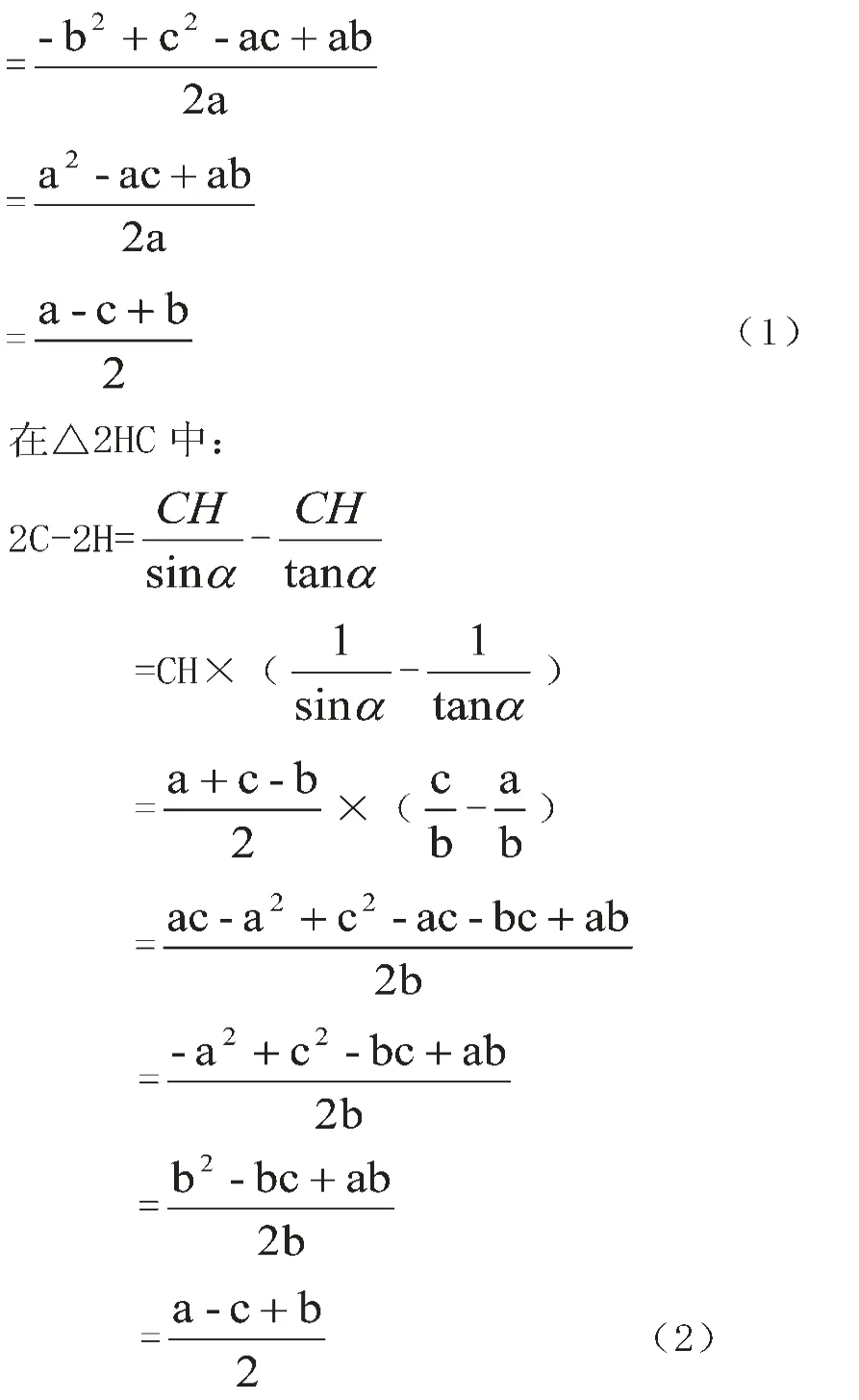
（1）式显然等于（2）式，从理论上保证了两段圆弧在直线12上是相切的。而且是内切，圆心距等于线段12的长。

这就从理论上保证了在第二象限中圆弧是光滑过渡连接的，根据对称性在其他象限也具有同样的情景。

二、“四心法”椭圆相对于理论椭圆的偏差

（一）定性分析

如图2所示，“四心法”画椭圆是用四段圆弧拼成了一个近似椭圆，这种绘图方法理论上保证了四段圆弧的光滑联接，但必然与理论椭圆存在偏差。左右两端外侧为近似椭圆，内侧为理论椭圆，靠近短轴的地方偏差小、靠近长轴的地方偏差大[3]33[4]10。

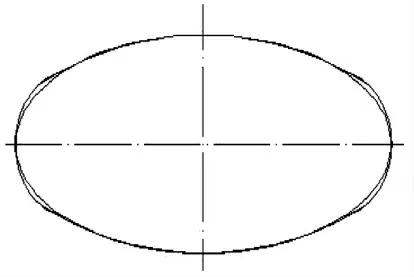
图2 近似椭圆与理论椭圆的对比

怎样定量地探索近似椭圆与理论椭圆的偏差值呢？

（二）定量分析

对于短长轴比例相同的椭圆族来说，如果长轴长，则作图的误差就大，从这个角度来说，我们可以反其道而行之，固定椭圆的长轴，研究长短轴比例多大时，椭圆误差最大[5]101。

为了方便对“四心法”画椭圆的方法进行偏差定量分析，同时也为了更具代表性，根据椭圆对称性的特点，仅取第二象限进行研究，这里对“四心法”画椭圆偏差进行评价的目的，并不是真正要求得到具体偏差值，仅仅是在给定长轴长度的椭圆族中，短长轴比例为何值时作图偏差取最大、最小值。

根据定性分析，只取靠近长轴的部分作为评价对象，如图3所示，即只研究Ab段圆弧与实际椭圆弧对应部分的偏差，为了客观地评价作图偏差，过点1作一条直线，让该直线的斜率大于直线1b的斜率，小于0，与椭圆弧和圆弧Ab分别交于m、n。将线段mn的距离作为评价对象。

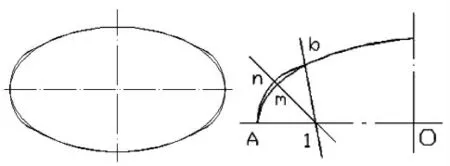
图3 近似椭圆偏差分析

优化分析。下面用优化方法来求解最大、最小作图误差：

1.确定评价对象——偏差大小的设计变量

短长轴比例系数设定为λ，直线1n的斜率设定为k。

则设计变量为：

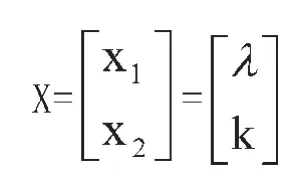
2.确定目标函数

为了求得mn之间距离的表达式，设椭圆长轴长为a（根据前面假设，a＞0且为定值）。根据图3坐标系及图1四心法画椭圆的步骤。可得椭圆弧的方程：

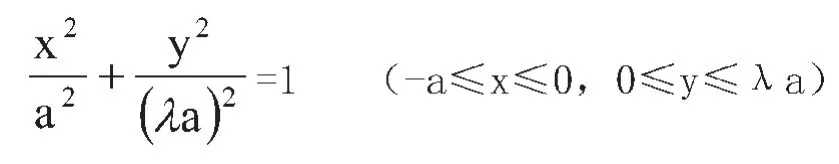
直线1b的方程为：

下面来求p（焦距），即图3中的O1：

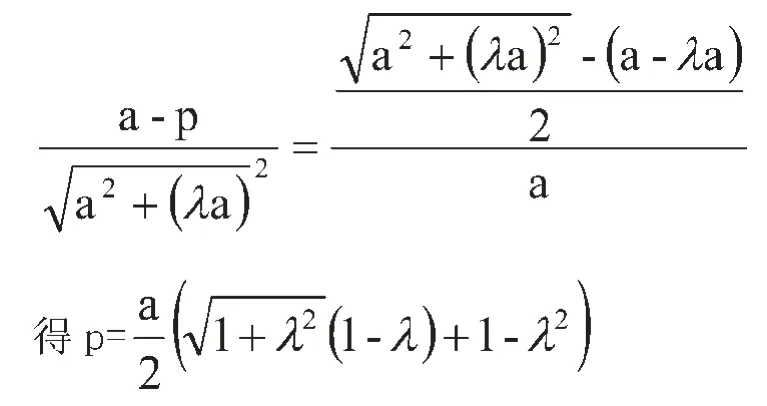
经过推导可确定误差最小时的目标函数为：

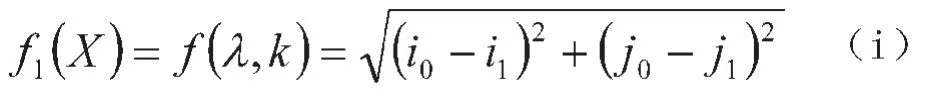
误差最大时的目标函数为：

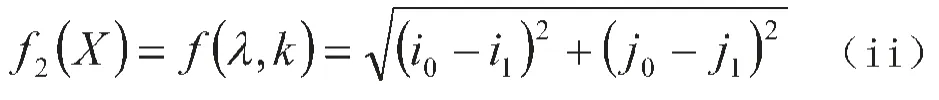
3.确定所求误差大小的约束方程

由短长轴比例系数λ（也就是x1）大于0而小于1得：

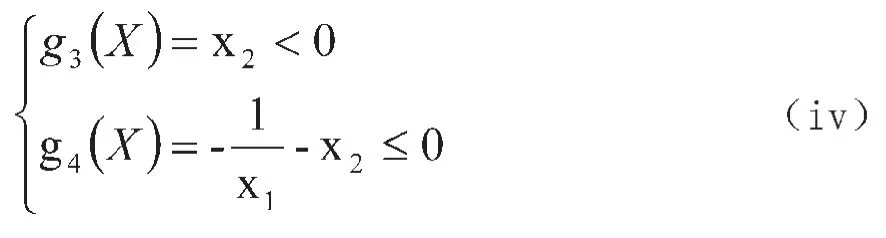
（三）MATLAB优化求值

MATLAB优化工具箱。MATLAB软件是美国的MathWorks公司开发的一款商业化数学软件。MATLAB中的优化工具箱，可以求解线性规划、非线性规划和多目标规划问题。使用MATLAB强大的计算及数据处理功能，可以快速确定理论椭圆与近似椭圆偏差的极值点，并求出极值，极大地减轻人的劳动，方法、结果明晰，工具箱中的二次规划函数能很好地解决二次曲线偏差距离计算问题[6]353，为以后数控加工中在不超差的情况下采用近似画法代替理论画法提供技术支撑。

优化求值。为了使计算更简单一些，可以设长轴为单位长度1，求出最大偏差值（如图4），根据参数化定义，求不同长轴时偏差轴时，只需放大相应倍数。

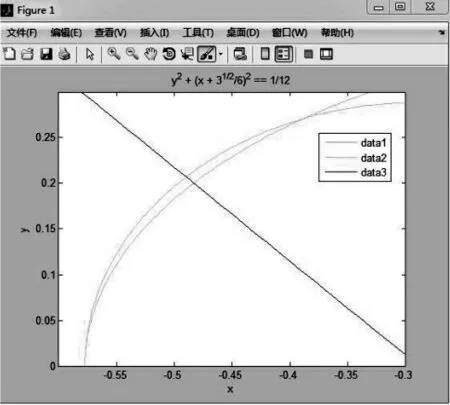
图4 椭圆偏差最大位置

编程求解：

＞＞x=sym（'x'）;

y=sym（'y'）;

x1=sym（'x1'）;

x2=sym（'x2'）;

y1=sym（'y1'）;

y2=sym（'y2'）;

ezplot（y.^2/（4-2*3^0.5）+3*x.^2/4==1/4，[-1，0，0，1]）;holdon%绘制椭圆

ezplot（（x+3^0.5/6）^2+y.^2==1/12，[-1，0，0，1]）;hol don%绘制圆形

[x，y]=solve（y^2/（4-2*3^0.5）+3*x^2/4==1/4，（x+3^0.5/6）^2+y^2==1/12，x，y）%求交点

x=double（x）;%对sym数组转换为double型

y=double（y）;%对sym数组转换为double型

K1=y（2）/（x（2）+sqrt（3）/6）;%斜率

K2=0;%斜率

KN=K1：0.1：K2;%调整间距，控制采样点的个数和运行实践

n=length（KN）

fori=1：n

k=KN（i）

[xs1，ys1]=solve（y1.^2/（4-2*3^0.5）+3*x1.^2/4==1/4，y1==k*（x1+3^0.5/6），x1，y1）;%椭圆与直线交点

[xs2，ys2]=solve（（x2+3^0.5/6）^2+y2.^2==1/12，y2==k*（x2+3^0.5/6），x2，y2）;%圆与直线交点

l（i）=sqrt（（xs1（2）-xs2（2））^2+（ys1（2）-ys2（2））^2）%求直线与椭圆及圆形交点的距离

end

LMAX=max（l）;

h=KN（find（l==LMAX））;

x3=-1：0.01：1

y3=h*（x3+3^0.5/6）

plot（x3，y3）;

axis（[-0.6，-0.3，0，0.3]）;

hold on

从表1、表2中的结果可以看出，当λ接近1时，即短长轴长度接近时，作图误差较小，为1时误差为0；当λ在0.24附近时，误差最大。