融入混沌与对立学习机制的二进制粒子群特征选择算法
袁明锋 步中华 王 强
1(重庆轻工职业学院大数据与信息产业系 重庆 401329) 2(青岛中石大科技创业有限公司 山东 青岛 266580) 3(青岛理工大学信息学院 山东 青岛 266580)
0 引 言
文本是现代社会存取信息和交流的主要方式,尤其在移动互联网时代,文本信息增长速度呈指数级。然而,文本中包含高维度信息化和非信息化特征,非信息化特征通常为冗余、噪声和不相关特征,对提取文本实质内容信息相对无效。因此,应该尽可能提炼文本中与本质内容密切相关的信息化特征,为进一步文本检索、文本分类及文本信息挖掘作支撑[1]。特征选择的主要任务即是从文本中得出信息化特征子集的过程[2]。然而,文本空间的高维度使得特征选择仍然是NP难问题。
本文提出一种基于改进二进制粒子群优化的特征选择算法。将特征选择问题形式化为粒子最优位置的搜索过程,引入对立学习机制对随机初始化过程做出改进,并利用混沌系统和基于适应度的动态惯性权重提升粒子寻优性能,通过建立的二进制粒子群优化对最优文本特征子集进行选择与搜索。同时,在评估粒子位置适应度过程中,引用词条方差和平均绝对差两种适应度评估方法,得出文本的最优特征子集。基于获得的最优特征子集,利用K均值算法对文本文档数据集进行了聚类分析,验证了在所获文本特征最优子集的前提下文本特征维度得到了有效降低,文档聚类准确率也得到了极大提升,有效证明了融入混沌和对立学习机制的二进制粒子群优化特征选择算法是有效可行的。
1 相关研究
传统文本特征选择算法主要包括文档频率DF[3]、互信息MI[4]、信息增益IG[5]和卡方统计CHI[6]等。DF以文档频率为依据,但忽略了词条在不同文档间的分布及词条关联性对文本内容的表征影响。互信息MI、信息增益IG和卡方统计CHI三种算法通过引入文本分类信息改善特征词条的文本表征能力,但同时也降低了特征维度约减上的效率,忽略了词条在不同文档间的分布、词条位置及词条相关性对于文本内容的表示影响。此外,目前初始语料库中通常会引入文本文档的分类信息,这使得以上算法在特征选择时无法进行无监督文本聚类分析。
除了以上传统特征选择算法,群体智能算法是目前针对文本特征选择求解的另一种主要方法。由于特征选择的NP属性,智能群体算法较强的寻优性能可以通过不断对初始解的迭代更新寻找接近最优的特征选择解,同时大幅降低特征维度,改善文本聚类效率[7]。相关研究中,文献[8]依据词条权重重要性设计基于遗传算法的特征选择算法GAFS,可以较高效率选择最优特征子集,而其邮件文本对GAFS的测试也验证了算法性能。文献[9]通过改进和声搜索过程设计了自适应特征选择算法,利用音调调整、限制特征域和内存合并率三种动态策略改进传统和声搜索,多维度数据集测试也验证了最优特征子集选择的有效性。粒子群算法是一种计算代价较小且收敛较快的智能算法。文献[10]提出基于粒子群优化的特征选择算法BPSOFS。利用新的动态惯性权重策略对粒子进化操作进行改进,而文本数据集的测试也证明新算法生成的文本聚类在准确度和效率上均有所提升。文献[11]结合遗传算法和并行协同进化算法求解特征选择,先利用遗传算法搜索特征子集,再进一步利用进化协同机制提升搜索效率,得到准确度更高的特征选择解。猫群算法也可用于求解优化问题。文献[12]通过修正猫群算法设计了特征选择算法,结果也证实利用猫群算法后的聚类明显然优于仅使用词条频率下的聚类效果。文献[13]设计了基于蚁群算法的无监督概率特征选择算法,算法利用特征相似性降低特征维度,引入矩阵记录特征共存率,通过特征提取概率函数对特征进行排序,并获取相关分值更高的特征子集作为聚类特征基础。文献[14]通过小生境改进了传统粒子群算法,以增强的粒子搜索性能对文本特征选择进行进化求解,获得的文本分类效率得到有效提升。总结已有工作,可将群体智能算法求解特征选择问题划分为以下几类:第一种是直接应用某一种智能群体算法将特征选择形式为一个优化问题,然后利用智能群体的寻优机制得到特征选择解;第二种是不同智能群体算法的结合再应用于特征选择求解,这类方法总体来说虽然可以结合不同智能群体算法在局部和全局寻优上的性能,但其搜索过程复杂性太高,可能导致无法得到满意的效率;第三种则是将传统方法与智能群体算法结合起来,首先在词条权重定义方面依然使用基于词条频率、文档频率、词条分布等传统要素,然后在此基础上,再利用智能群体算法根据现有词条权重根据所定义的特征相关性分值寻找最优的特征子集。本文将利用第三类方法,首先利用一种改进的词条权重计量方法得到初步的特征初选,然后设计一种改进的二进制粒子群优化方法进行特征子集选择。为了提升粒子群的搜索能力,引入了混沌系统和对立学习机制对粒子的随机搜索方向和初始种群分布进行了优化,更好地实现特征选择,而后续基于所选特征子集的聚类结果也很好地验证了这一特征选择方法的有效性。
2 词条权重计算模型
令集合D包含n个文档 ,表示为D={d1,d2,…,di,…,dn},其中:di表示D中的第i个文档;n表示集合中的文档总量。利用传统的词频逆文本频率指数TF-IDF方法,文档i可表示为向量di={wi,1,wi,2,…,wi,j,…,wi,t},文档长度为t,即所含词条数量,wi,j为通过TF-IDF计算的文档i中词条j的权重值,且:
(1)
式中:TF(i,j)表示文档i中词条j的频率;n表示文档集合文档总量;DF(j)为包含词条j的文档数量;IDF(i,j)为文档频率倒数。
本文将利用一种新的词条权重计算方法NTW,改进思路主要在于:首先,TF-IDF方法中,主要用到词条的文档频率倒数IDF,而忽略了每个词条的文档频率DF,由于当词条出现在大多数文档,则DF可以通过增加的权重分值影响其重要性,因此,DF将作为一个参数考虑在新的词条权重计算中。其次,TF-IDF方法忽略了文档中所有词条的数量,该参数有助于选择较少数量的信息化特征。最后,最大词条频率可用于区分文档词条,若文档包含大量词条,则表明词条特征重要性要小于少数量词条的情形。基于以上三个因素的考虑,改进词条权重计算方法NTW定义为:
(2)
式中:ai表示文档i中所选特征数量;maxf(i)表示文档i中的最大词条频率。
通过向量空间模型VSM,可根据词条权重wi,j将整个文档集合D表示为:
(3)
3 二进制粒子群优化算法
粒子群算法是受鸟类、鱼群社会行为启发得到的一种元启发式算法。粒子群中的个体称为一个粒子,种群由S个粒子构成,每个粒子代表在d维空间内的一个候选问题解。粒子i在d维空间内的位置向量为Xi=(xi1,xi2,…,xid),粒子速度向量为Vi=(vi1,vi2,…,vid)。所有粒子在搜索空间内移动以寻找其全局最优解,粒子的移动会受到自身已知的个体最优位置pbest和种群的已知全局最优位置gbest的影响。粒子i的个体最优位置可表示为pbesti=(pbesti1,pbesti2,…,pbestid),种群的全局最优位置可表示为gbesti=(gbest1,gbest2,…,gbestd)。粒子位置优劣由预定义的适应度函数评估。粒子i的速度和位置更新方式如下:
vid(t+1)=w×vid(t)+c1×r1×(pbestid-xid(t))+
c2×r2×(gbestd-xid(t))
(4)
xid(t+1)=xid(t)+vid(t+1)
(5)
式中:r1和r2为[0,1]内均匀分布的随机数;c1和c2分别为认知权重因子和社会权重因子,通常固定取值在[0,2]之间;w为[0,1]间的惯性权重,用于控制粒子先代速度的影响。较大惯性权重w利于粒子对新区域的全局勘探,较小惯性权重w利于粒子的局部开发,因此,惯性权重可以均衡全局勘探和局部开发过程。
传统粒子群优化算法是连续空间内的粒子群算法,即粒子位置可在连续空间位置上移动。对于特征选择问题而言,当以粒子位置代表特征选择解时,单个特征是否被选择仅有选择与不选择两种情形,因此,粒子位置仅有两种取值情形,此时可以二进制形式定义粒子位置。粒子位置更新代表对应位置比特值的改变,粒子速度则代表粒子位置改变为1的概率。利用S形函数将连续位置信息映射为二进制位置信息。速度的S形函数定义为:
(6)
式中:Sig(vid(t+1))为d维比特值为1的概率。粒子新位置更新方式为:
(7)
式中:rand(0,1)为[0,1]间的随机数。
4 基于混沌和对立学习的二进制粒子群优化特征选择算法COBPSO
4.1 特征选择模型
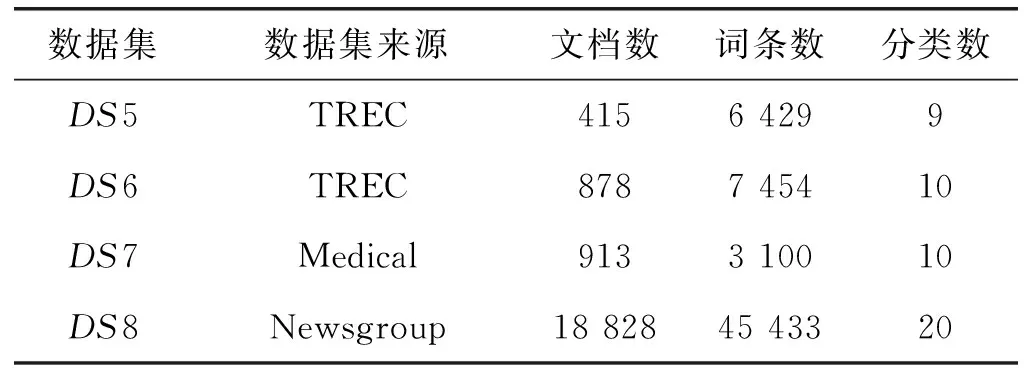
特征选择的目标是按某种标准从文本词条中提炼出与文本内容更为贴近的文本特征,即尽可能消除非信息化的冗余特征,得到最优的信息化特征子集。令Fi为文档i的特征集合,表示为向量Fi={fi,1,fi,2,…,fi,j,…,fi,d},其中,j为特征序号。经过特征选择后,新的信息化特征子集SFi={sfi,1,sfi,2,…,sfi,j,…,sfi,m},其中,m为新的特征长度,且m 以粒子位置表征特征选择候选解,即一个粒子代表一种选择的文本特征子集,表示为表1所示形式。编码中上层向量代表特征序号(维度),下层向量代表粒子在各维度上的二进制位置,粒子搜索的空间维度d对应可能文本特征数量。二进制向量Xi=(xi1,xi2,…,xid),若xij=1,则表明粒子i位置所代表的特征选择候选解中,特征j选择为信息化特征;若xij=0,则表明粒子i位置所代表的特征选择候选解中,特征j不被选择定信息化特征,即不包括在最优特征子集中。 表1 特征选择解编码结构 适应度函数用于计算文档中的特征相关性分值,即为评估个体粒子位置所代表的特征选择解的优劣。本文引用两种特征相关分值计算方法,一种是词条方差法TV,一种是平均中位数法MM。 词条方差法TV可以准确反映特征对文本类别的区分能力,选择以具有类别信息的特征为主,不足是会忽略特征间的相关性。其目标是通过计算与均值间的方差分配特征相关性分值,该方法的出发点是考虑所有文档中非均匀分布的特征比均匀分布特征更能较好描述文档含义。词条特征的TV值定义为: (8) (9) 平均中位法MM则可以尽可能选择具有相关性的特征,通过计算平均值与中位值间的绝对差分配特征相关性分值。词条特征的MM值定义为: (10) 式中:median(xt)表示特征t的中位值。 令D为文档集,文本预处理后特征集合为T,以T={t1,t2,…,tf}代表初始特征集合,特征数量为f。通过词条方差TV计算特征相关性分值后,将特征集合T中的特征按照TV值降序排列,令FS1={t11,t12,…,tq}为通过TV选择的特征子集,tq代表TV所选特征数量为q,且q< 利用特征合并操作U建立新特征子集FS3,即合并特征子集FS1和特征子集FS2,表示为: FS3=FS1∪FS2 (11) 若特征子集FS3包含U个特征,则U≥{q,l}。 利用特征交叉操作I建立新的特征子集FS4,即交叉特征子集FS1和特征子集FS2,表示为: FS4=FS1∩FS2 (12) 若特征子集FS4包含I个特征,则I≤{q,l}。 传统元启发式算法以随机方式生成初始种群,然后逐步迭代接近全局最优解改善种群个体,其搜索过程在满足预定义终止条件时结束。因此,算法的收敛速度与初始种群与最优解间的距离直接相关。最差情形中,最优解离随机初始种群较远,则搜索寻优可能无法完成。对立学习可以通过同步考虑当前解及其对立解改善候选解的质量,收敛速度可以通过同步考虑当前解及其对立解予以改善。研究表明,约50%随机初始解会比其对立解离最优解更远。因此,将随机初始解及其对立解联合考虑在初始种群中,可以加快搜索收敛速度。 定义1对立数。令x为区间[l,u]内的实数,x∈[l,u],其对立数x′为: x′=u+l-x (13) 基于对立学习的种群初始化步骤如算法1所示。 算法1对立学习机制的粒子种群初始化 输入:种群规模S。 输出:规模S的粒子集合X。 1.随机生成粒子数为S的初始种群{X}; 2.fori=1 toSdo //所有粒子上遍历 3.forj=1 toddo //所有位置维度上遍历 //粒子位置的对立点 5.endfor 6.endfor 7.X″=X∪X′ //融合原始粒子和对立粒子为新种群 8.计算新种群X″中粒子的适应度; 9.根据适应度对X″中的粒子作降序排列; 10.以排序前S的粒子种群X作为最终初始种群; 11.返回初始种群X。 二进制粒子群优化算法中,粒子速度更新与三个成分相关:粒子先前速度vid(t)、认知成分pbestid-xid(t)、社会成分gbestd-xid(t)。先前速度即前次迭代的粒子速度,认知成分代表粒子自身的信息,社会成分为种群保留的信息。先前速度对当前速度的影响由惯性权重w决定,因子c1和r1、c2和r2则分别控制认知成分和社会成分的权重。本文提出一种动态惯性权重机制取代固定惯性权重,使惯性权重随搜索迭代过程进行自适应更新,以适应于粒子搜索过程中在前期的局部开发和后期的全局勘探间取得均衡。首先将粒子i的适应值定义为: (14) 式中:K为粒子聚类量;d(cl,cg)为聚类cl和cg间的距离;DIA(ck)为聚类k的直径。同时: (15) (16) 式中:DIS(x,y)表示粒子x与粒子y间的欧氏距离。 由于需要寻找更高聚类内相似度和更低聚类间相似度的粒子聚类,因此,适应值更高的粒子应优先选择。换言之,基于适应值的动态惯性权重将分配高惯性权重至低适应值粒子,促进该类粒子在搜索空间内对未知区域的全局勘探;而会分配低惯性权重至高适应值粒子,促进该类粒子在搜索空间内作进一步局部开发。因此,粒子惯性权重将依据粒子当前的适应值与当前最优适应值进行计算: (17) 式中:fiti为粒子i的适应值;fitbest为全局最优粒子gbest的适应值。基于动态惯性权重,粒子的速度更新可改进为: vid(t+1)=fwi×vid(t)+c1×r1×(pbestid-xid(t))+ c2×r2×(gbestd-xid(t)) (18) 由式(18)可知,融入适应值的动态惯性权重至粒子速度更新可以根据粒子当前状态动态调整粒子速度,较大的惯性权重可以增加较低适应值粒子的速度步长,促进其搜索空间内的全局勘探过程;而较小的惯性权重可以减小较高适应值粒子的速度步长,促进其搜索空间内的局部开发过程。 粒子速度更新的第二部分和第三部分分别反映粒子的认知信息和社会信息,这两部分主要受学习因子c的影响。越大的学习因子c1会使粒子更快地朝自身已知最优位置pbest移动,越大的学习因子c2会使粒子更快地朝全局最优位置gbest移动。通常,两个学习因子设置为相同权重。本文将改变学习因子取值以控制认知和社会信息对粒子速度更新的影响,设计基于对立学习的粒子替换策略,避免粒子在局部最优解上早熟,促进粒子向未知区域继续搜索。具体做法是:首先,生成全局最优粒子gbest的对立位置,用于替换最差适应度粒子gworst,从而保留gbest粒子的较优解,利用最差粒子gworst搜索未知区域。对于所有粒子,除gworst以外,c1和c2设置为2,而gworst粒子的c1和c2分别设置为3和1。融入对立学习的差异化学习因子设置可以使粒子移动方向的更新朝自身最优继续移动。 混沌是一种非线性的动态随机非重复决策系统,表征对初始条件的敏感依赖性,也是一种无限非稳定的周期运动。由于混沌的可遍历性及非重复性,它可以更有效地实现比随机搜索(由随机值r1和r2决定)更广泛的搜索过程。将混沌系统融入二进制粒子群优化算法中可以增强搜索能力,更好预防陷入局部最优解。本文利用sinusoidal混沌映射生成混沌序列,形式化为: CH(t+1)=μ×CH(t)2×sin(πCH(t)) (19) 式中:CH(t)表示迭代t时的混沌值,CH(t)∈[0,1],初始值CH(0)在不等于0、0.25、0.5、0.75和1的情况下随机生成;控制参数μ∈(0,2.3],用于控制混沌值的变化行为,可变μ对于混沌映射值的生成影响可参考文献[15]中的讨论。 本文利用混沌系统的非重复性,生成更均匀的随机数序列提升粒子的搜索速度,主要方法是:利用sinusoidal映射公式生成的混沌序列取代粒子更新中的随机值r,则基于sinusoidal映射的改进粒子速度更新方式为: vid(t+1)=fwi×vid(t)+c1×CH×(pbestid-xid(t))+ c2×(1-CH)×(gbestd-xid(t)) (20) 特征选择算法COBPSO过程如算法2所示。 算法2改进二进制粒子群优化特征选择算法COBPSO 输入:c1,c2,fw,CH,pbest,gbest,gworst,X,count,S。 输出:全局最优粒子gbest。 1.算法相关参数初始化; 2.随机生成初始混沌值CH(0); 3.利用算法1的对立学习机制生成粒子初始种群; 4.搜索个体最优pbest、全局最优gbest和全局最差gworst; 5.whilenot satisfy maximum iterationsdo //若干次迭代寻优 6.forp=1 toSdo //所有粒子上遍历 7.根据式(17)计算自适应惯性权重值; 8.ifcount>δandxpisgworstthen 9.设置不均等学习因子(c1,c2); 10.else 11.设置均等学习因子(c1,c2); 12.endif 13.forq=1 toddo //所有位置维度上遍历 14.根据式(19)更新粒子混沌值CHq; 15.根据式(20)更新粒子速度; 16.根据式(5)更新粒子位置; 17.endfor 18.endfor 19.forp=1 toSdo //所有粒子上遍历 20.iff(xp)>f(pbestp)then 21.pbestp=xp; 22.iff(xp)>f(gbest)then 23.gbest=xp; 24.endif 25.endif 26.iff(xp) 27.gworst=xp; 28.endif 29.endfor 30.if全局最优粒子gbest未发生变化then 31.count=count+1; 32.else 33.count=0; 34.endif 35.选择全局最差粒子gworst; 36.ifcount<δthen 37.对全局最差粒子gworst作变异; 38.else 39.对全局最差粒子gworst作对立学习更新; 40.endif 41.endwhile 42.return最优粒子gbest作为最优特征选择子集。 算法过程描述:算法输入参数:学习因子、惯性权重、混沌映射值、粒子个体最优解、全局最优解、全局最差解、种群粒子当前位置集合、全局最优解状态因子、种群规模,输出为全局最优粒子。步骤1和步骤2分别对粒子群优化的相关参数和混沌映射值作初始化。步骤3利用算法1的对立学习机制对粒子种群进行初始化,即得到特征选择解的初始分布,步骤4根据适应度函数计算个体最优解、当前种群的全局最优解和全局最差解,由于还未迭代寻优,个体粒子当前位置即可视为其个体最优解。接下来是若干次的迭代寻优过程,即步骤5-步骤41的过程。迭代过程的第一个for循环(步骤6-步骤18)遍历所有种群粒子,步骤7计算粒子的惯性权重,步骤8和步骤9对最差粒子个体的学习因子作不同设置,步骤 11则对非最差粒子个体的学习因子作相同设置。步骤13-步骤17针对单个粒子的所有维度位置进行更新,首先在步骤14更新混沌值,然后在步骤15和步骤16分别计算粒子每个维度上的速度和位置。迭代的第二次for循环(步骤19-步骤29)依然遍历所有种群粒子,目标是更新个体最优解、全局最优解和全局最差解三个粒子位置。步骤21表明,若当前粒子适应度大于其个体最优解,则将其个体最优解更新为当前的粒子位置;进一步,若当前粒子适应度大于全局最优解,则在步骤23将当前粒子设置为全局最优解;步骤27表明,若当前粒子适应度小于全局最差解,则更新全局最差解为当前粒子位置。步骤31表明,若全局最优解不发生变化,则全局最优粒子状态count递增1;否则,在步骤33将该因子重置为0。步骤35选取当前种群中适应度最差的粒子gworst。步骤36-步骤40根据变异(步骤37)或对立学习机制(步骤39)对全局最差解gworst进行更新。具体地,变异操作可根据变异概率决定是否以当前的全局最优粒子的对立点相应维度上的位置替换全局最差解gworst的对应维度位置;而对立学习则是以全局最优粒子gbest的对立点粒子替换为当前的全局最差解gworst。达到最大迭代次数后,最后在步骤42输出最优粒子位置,并解码出相对应的特征选择解。 图1为完整的文本特征选择及聚类分析流程。首先,需要对输入文本数据集作预处理,包括词语分割、移除终止词汇、提取词干,词条权重计算方面可以分别以传统的TF-IDF方法和本文中的NTW方法进行,再根据词条权重将文本表征为向量空间模型。然后,进入基于混沌与对立学习机制的二进制粒子群优化文本特征选择步骤,该过程中会利用混沌系统和对立学习机制对二进制粒子群优化的特征选择寻优过程进行改进,提升搜索效率和寻优准确度;此外,在粒子位置所代表的特征选择解的质量评估方面,同时引用了词条方差TV和平均中位数MM两种方法,并针对两种可能的特征选择解,引入特征合并和特征交叉机制生成最优特征子集,这样可以同步考虑特征对文本类别的区分能力和特征间的相关性。最后,在所选择的最优特征子集的基础上,引用K均值算法对文本数据集进行聚类,并对聚类结果作准确性和特征降维方面的分析。 利用MATLAB编写测试程序,利用表2中由计算智能实验LABIC提供的八种基准文本数据集测试算法性能。表2给出了数据集来源、所含文档数、词条数、文本分类数。测试数据集合中,数据集DS1为技术报告类文集,数据集DS2为Web网页搜索文集,数据集DS3-DS6均是文本信息的检索内容,实质内容各有不同,数据集DS7为医学信息内容,数据集DS8为新闻组播内容。测试文本数据覆盖了众多文本信息领域,可以很好地测试本文的特征选择算法的稳定性和适应性。 表2 测试文档数据集 续表2 利用F度量FM和准确率AC两个主要指标度量特征选择后的文本聚类性能。F度量根据给定的分类标签通过计算精确率P和召回率R计算,分别表示为: P(i,j)=ni,j/nj (21) R(i,j)=ni,j/ni (22) 式中:ni,j表示聚类j中分类i的成员数;ni表示分类i中的成员总数;nj表示聚类j的所有成员数。聚类j的F度量FM计算方式如下: (23) F度量值FM(j)可用于衡量来自聚类j中分类i的正确文档的比例。式(24)则可用于计算所有聚类K的F度量值: (24) 准确率AC用于计算正确分配至每个聚类中的文档比例,表示为: (25) 式中:n表示所有文档数量;K表示文本聚类数。 文本文档聚类分析的流程是:首先,对文本信息进行词语分割、终止词移除、词干提取,利用词条权重策略计算词条权重值(本文可以根据传统TF-IDF方法和改进策略NTW分别计算),并基于词条权重将文本集合表示为向量空间模型;然后,利用融入混沌和对立学习的二进制粒子群特征选择算法COBPSO进行最优特征子集的选择,该算法执行过程中可以词条方差法TV和平均中位数法MM分别作为适应度函数进行粒子优劣评估,且还可以分别对两种适应度评估下的特征子集作合并和交叉处理,因此,这一过程中有以下几种算法组合:BPSO-TV、BPSO-MM、BPSO-U和BPSO-I;最后,基于前一步骤中得到的最优特征子集,利用经典的K均值聚类算法对文本文档集合进行聚类分析,评估聚类指标。因此,本文可以测试的相关算法可总结于表3的形式。 表3 测试算法组合 性能对比算法选择未作特征选择的传统K均值算法、基于遗传算法的特征选择算法GAFS[8]和基于传统二进制粒子群算法的特征选择算法BPSOFS[10]进行对比分析。对于两种智能群体算法而言,种群规模设置为200,种群个体进化的最大迭代次数设置为400,GAFS算法的遗传交叉概率设为0.7,遗传变异概率设为0.3,BPSOFS算法的粒子惯性权重最小值设为0.4,最大值设为0.9,两个学习因子均设置为0.5。 图2所示是在八种测试数据集中,在三种不同的特征选择策略和不同的词条权重计量方式以及不同的特征子集生成方式下得到的特征选择量。COBPSO为本文设计的融入混沌和对立学习机制的二进制粒子群特征选择算法,BPSO则为传统二进制粒子群特征选择算法,GA为基于遗传的特征选择算法。词条权重计量可以分别利用TF-IDF和NTW进行计算,特征子集生成时评估方式可以通过TV和MM,以及TV与MM的合并或交叉机制予以进行。八种测试数据集覆盖文本广泛,可以较好测试算法对文本特征降维的适应性和稳定性。从结果来看,COBPSO算法的特征降维度效果明显优于BPSO和GA。本文在二进制粒子群优化中引入对立学习机制改善初始种群所代表的候选解的质量,加速了粒子的寻优过程,同时,利用sinusoidal混沌映射生成混沌序列的方式也可以明显提升粒子的搜索速度,以及基于适应度的粒子惯性权重调整方式均起到了对二进制粒子群优化的性能改进作用,进而相应提升的特征选择的准确性,使得相关性更好的特征拥有更大的机会在寻优过程中得以保留。在相同的特征选择适应度评估方式下,本文的NTW方法可以略微减少特征选择量,证明新的词条权重计量方法是有效可行的。利用TV和MM两种特征选择适应度评估方式在特征选择量方面并没有反映出明显区别,而特征交叉I是可以有效降低特征选择量的。特征合并U交没有明显增加最终的特征选择量,这说明两种特征选择适应度评估方式TV和MM所生成的特征子集大部分是相交的,均能够以较高的准确性选择出反映文本实质内容的特征子集,仅在反映文本类别的区分能力的特征和相关性特征上会出现个别不同的特征个体,并不会相互颠覆文本的最优特征子集。 表4为聚类评估指标的比较结果。表格最右侧的K均值算法表示未使用任何特征选择的传统聚类算法,明显其聚类性能是最差的,这是因为不做文本特征选择会导致很多冗余和非信息化特征在聚类过程中被考虑,噪声太大,聚类准确性较差。使用BPSO和GA这类群体智能算法进行文本特征选择可以明显提升文本聚类性能。同时,比较传统二进制粒子群优化和遗传算法的特征选择,本文设计的基于混沌与对立学习机制的二进制粒子群优化特征选择算法在多数测试数据集中可以得到更高的准确率和F度量值,这说明所生成的特征子集准确度更高,特征空间维度得以有效降低。总体而言,新的词条权重计量方式NTW比传统计量方式TF-IDF得到的聚类性能也略有上升。利用TV和MM两种不同的相关性分值计算方式后,对所生成的特征子集作出特征合并或特征交叉后,对聚类性能也可以产生较积极的影响,各项聚类指标均有一定程度提升,说明融合不同评估方法的特征子集处理机制是有效可行的。 表4 聚类评估指标对比 续表4 图3是利用K均值算法对经过特征选择后的文本文档进行聚类所需要的时间的比较。若不经过文本特征选择,直接以K均值算法进行文档聚类,如结果所示,其聚类迭代时间是最短的,但是其文本特征维度没有降低,且其聚类准确性较差。此外,利用本文的基于混沌和对立学习机制的二进制粒子群算法的特征选择后的聚类效率显然高于另外两种智能群体算法BPSOFS和GA,这说明对立学习机制下的粒子群初始化可以有效改善初始粒子的分布,加速粒子寻优搜索速度;而融入混沌映射的随机粒子搜索机制也可以提升粒子搜索速度,从而得到最优的特征子集,提升聚类效率。同时,相比传统的词条权重计量方法TF-IDF,利用本文新提出的词条权重计量方法后,聚类效率略有提升,说明NTW中所考虑的三个要素对于定义词要权重是具有重要影响的。而在利用相同的词条权重计算方法和相同特征选择策略下,通过特征合并和特征交叉也可以相应提升聚类效率,这说明综合词条方差和平均中位数两种特征选取标准,可以整合两者优势,对精确选取相关性更好的最优特征子集是有益的。 本文提出一种基于改进二进制粒子群优化的特征选择算法。将文本特征选择建模为粒子最优位置的搜索过程,引入对立学习机制改进随机种群初始化,并利用混沌映射和基于适应度的动态惯性权重提高粒子寻优性能。通过改进的二进制粒子群优化求解最优文本特征子集选择解。同时,在评估粒子位置适应度过程中,结合词条方差和平均绝对差两种特征评估方法的优势,得到最优文本特征子集。基于获得的最优特征子集,进一步利用K均值算法对文本文档数据集进行了聚类分析,验证了在所获文本特征最优子集的前提下文本特征维度得到了有效降低,文档聚类准确率也得到了极大提升,说明融入混沌和对立学习机制的二进制粒子群优化特征选择算法是行之有效的方法。4.2 特征选择解编码

4.3 适应度函数
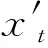
4.4 基于对立学习机制的粒子种群初始化
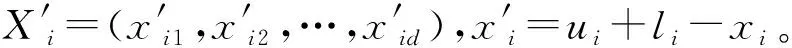
4.5 基于适应值的动态惯性权重机制
4.6 基于对立学习的学习因子调整
4.7 基于混沌理论的随机搜索机制
5 实验与结果分析
5.1 测试文本说明

5.2 评估标准
5.3 测试算法说明

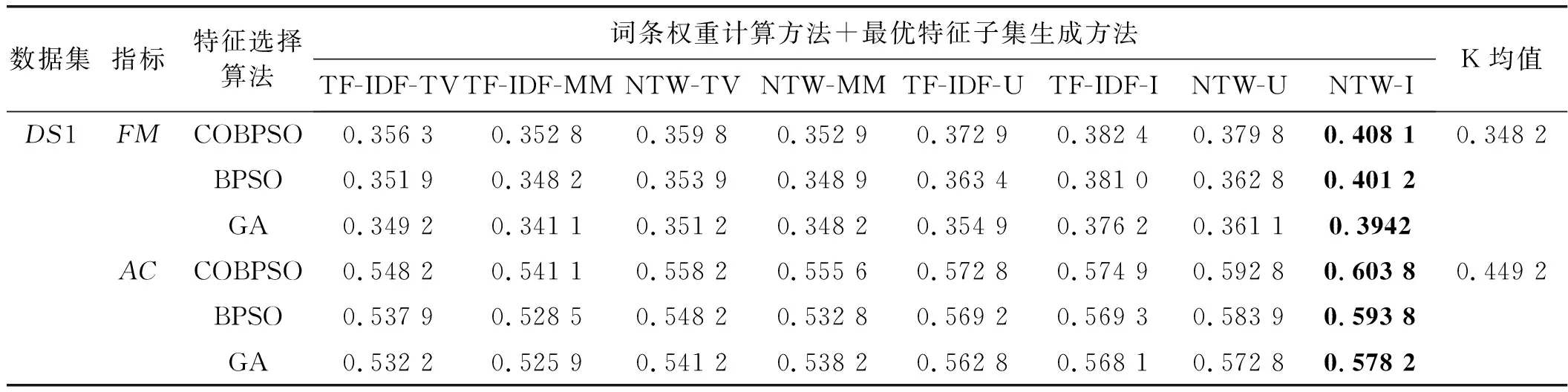
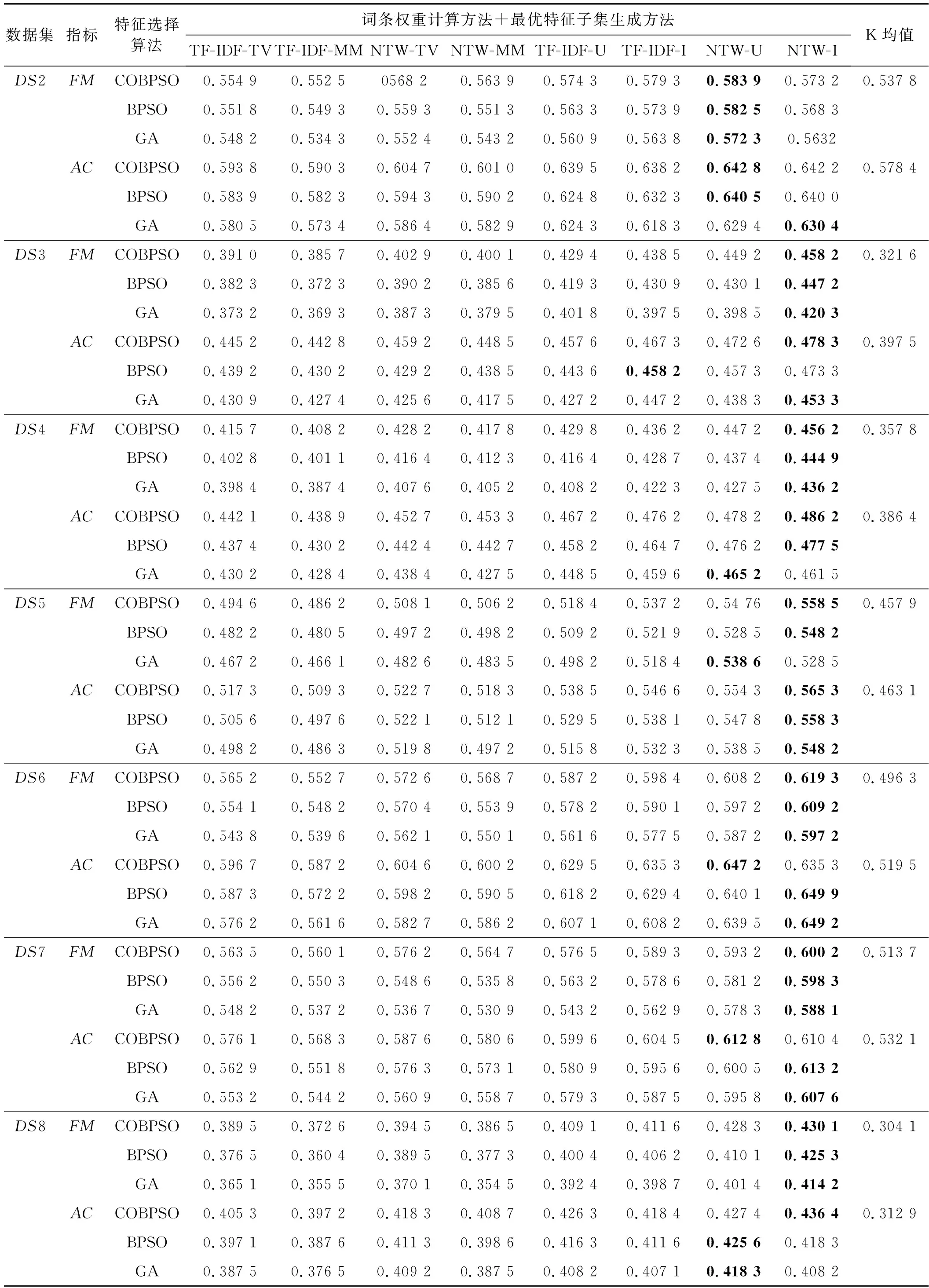
5.4 实验结果
6 结 语

