基于反向学习和可行性准则交叉的约束差分进化算法
段 伟 徐 斌
(上海工程技术大学机械与汽车工程学院 上海 201620)
Crossover operator Engineering application
0 引 言
差分进化算法(Differential Evolution, DE)是一种新兴的进化搜索算法[1],具有结构简单、鲁棒性强、参数少等特点,在全局优化过程中得到广泛的应用。但是实际的工程优化设计问题通常包含各种复杂约束,传统的DE算法在求解这类问题时存在一定的局限性,通常需要加入额外的约束处理技术。常用的约束处理技术主要包括惩罚函数法、可行性法则和多目标优化方法等[2]。王庆贺等[3]对约束多目标问题中进化个体对各个目标的影响动态变化进行了分析,提出了基于各分目标惩罚函数,合理地动态分配目标函数值,提高种群个体对目标值影响的准确性;Deb[4]利用约束违反度值描述约束程度并参与到个体适应度值的比较中,综合考虑影响种群个体大小的条件,挑选出满足条件的子代种群,确定种群的进化方向;Gong等[5]提出了一种基于Pareto占优准则的多目标约束处理方法,将被子代个体Pareto支配的父代个体用子代个体替代,并采用e-dominance对储备的非支配个体进行更新归档。
反向学习[6]是通过对称点找到数值对应的镜像点,有利于实现随机点的均布,文献[7-10]将反向学习方法应用于算法中,扩大了种群的搜索范围,避免无效搜索。因此本文利用反向学习进行种群初始化,并对进化后的个体进行反向边界处理;同时在Wang等[11]的启发下,对Deb约束处理后的目标个体和实验个体加设可行性算子,并进一步进行交叉处理,提出一种基于反向学习和可行性准则交叉的约束差分进化算法(DEOC) 。为了验证DEOC算法的性能,采用13个标准测试函数进行仿真实验,并将其应用于蜗轮齿圈和焊接梁优化问题中,验证DEOC算法的有效性。
1 基本理论
1.1 约束优化问题
约束优化的基本形式为:
minf(x)x∈Ω
(1)
s.t.gt(x)≤0,t= 1,2,…,q
ht(x) = 0,t=q+ 1,q+ 2,…,m
式中:x=(x1,x2,…,xD)是一个D维的向量个体;f(x)为目标函数,gt(x)是第t个非等式约束条件;ht(x)是第t-q个等式约束条件。一般将等式约束变形成不等式约束形式:
|ht(x)|-δ≤0t∈{q+1,q+2,…,m}
(2)
式中:δ为一个正的容忍值,一般取10-4。一个解x的约束违反值为:
(3)
G(x)的大小反映个体x违反约束条件的程度。
1.2 差分进化算法
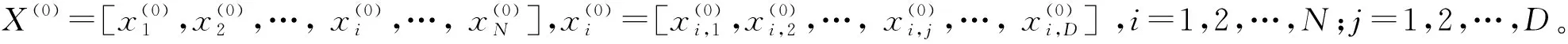
(4)
1) 变异操作是差分进化算法的主要操作,它决定了算法种群的进化方向,最为常用的变异策略为:
(5)
式中:xr1、xr2、xr3表示选择种群中三个互异个体;F∈[0,1]为缩放因子。
2) 交叉操作:利用式(5)得到的变异后个体v与x执行二项式交叉操作,生成新个体:
(6)
式中:CR∈[0,1]为交叉率;jrand表示[1,D]中的一个随机整数。
(7)
1.3 Deb准则
Deb准则是应用最广泛的约束处理方法之一,与其他方法相比,Deb准则不需要定义额外参数,只需根据问题的目标函数和约束违反值就筛选出绝对优秀的目标个体。对于给定的两个个体xi和ui,当满足下列条件之一时,称ui比xi好:
1)G(xi)=0且G(ui)=0,并且f(ui) 2)G(xi)>0且G(ui)=0。 3)G(xi)>0且G(ui)>0,并且G(ui) 本文提出DEOC算法着重解决约束优化问题,基于反向学习方法对初始种群和进化种群的边界选择进行进一步优化,扩大算法的搜索范围,同时在Deb准则中加入交叉算子,储备满足快速收敛的失效个体。通过进一步交叉进化,优秀的失效个体重新归位到种群,最终提高算法的收敛速度和稳定性。 基本的差分进化算法的初始种群是模仿生物进化的方法,通过随机的方式产生的,这样产生的随机数就有可能出现局部化,造成初始种群个体相似,初始的搜索范围狭小,从而进化提前停滞,导致算法所搜寻的优秀个体无法代表整个搜索域。而通过对随机产生的初始种群进行反向学习后,提高了初始生物个体分布的均匀性,防止初始种群聚集在某一区域,提高了初始种群的质量。DEOC算法产生初始种群的伪代码如下: 1. 通过式(4)产生初始种群X(0)。 2. Fori=1 toN 3. Forj=1 toD 5. End for //反向学习的初始个体 7. End for //X(0)为初始种群,X^(0)为反向种群,W为混合种群 9.从W中挑选N个适应值小的个体更新种群X(0)。 在处理约束问题时,变异交叉后的个体ui易跳出初始边界 [xmin,j,xmax,j],造成种群有效个体减少,降低算法的收敛速度并易使算法陷入局部最优。所以要对跳出边界的个体uλ及时纠正,常用的边界处理的方法是用u^λ=xmin,j+rand[0,1]×(xmax,j-xmin,j)代替失效个体uλ,但是利用这种方法产生的u^λ失去了变异交叉对种群个体的进化影响。 为了保留算法变异交叉操作对跳出边界个体的影响性,本文学习反向学习精英选择策略[12]对于处理变异交叉后的中间群体的方法,采用式(8)所示的反向边界处理并吸收的方法,调整个体uλ中基因ui,j大小,使uλ跳回边界区域内,同时该方法又可以增加有效个体的多样性,保证算法的全局搜索能力。 (8) 本文发现Deb准则没有完全发掘不可行域中个体的能力,没有利用可行个体和与之对应变异交叉后个体的关系,即没有保留个体在进化过程中的进化能力。为了保证种群个体都具有更强的学习能力,提出一种基于可行性准则交叉算子,充分挖掘部分不可行解携带的信息。如图1所示,当ui满足G(xi)<0,G(ui)>0,并且f(ui) 误除个体hi具有更小的目标函数,更接近最优解的特点。由图1可以发现hi和xi的直线方向上可能会产生适应度函数更小的个体,因此对hi和xi进行交叉处理,产生下一代个体zi,选取zi=[0,1]×(hi+xi),将zi储存在Z中。根据适应度值评估种群Z与X,并更新种群X。基于可行性准则交叉算子的伪代码如下: 1.Z=∅; 2. Fori=1 toN 3. ifG(xi)=0&G(ui)>0&f(ui) 4.hi=ui;zi=rand[0,1]×(hi+xi);Z=Z∪zi; 5. End if 6. End for 7.P=Z∪X; 8. 从P中挑选出适应值小的N个个体更新种群X。 将上述3部分改进内容融入基本差分进化算法,得到改进的DEOC算法,迭代过程如图2所示。 为了验证DEOC算法的有效性,选取了13个标准约束优化测试函数进行实验仿真[13]。这13个测试函数的目标函数包含线性和非线性方程,其中g01、g04、g07、g11和g12五个测试函数的目标函数为二次方程。约束函数包含线性不等式约束、非线性等式和不等式约束,其中g03,g05、g11和g13四个测试函数中含有等式和不等式约束。另外,为了进一步验证DEOC算法在实际工程中的有效性,将其用于蜗轮齿圈和焊接梁优化设计问题。 将DEOC算法与基本的DE算法进行比较,两种算法参数设置如下:N=40,F=0.8,CR=0.9,运行30次,最大评估次数为240 000次。两种算法在求解g03、g06、g07、g09、g10、g11、g12这7个问题时,差别不明显,因此,图3给出了基本DE算法和改进DEOC算法在求解g01、g02、g04、g05、g08和g13等6个函数的收敛曲线。 可以看出,DEOC算法与基本的DE算法相比,在收敛速度和收敛精度上都有很大的优势。在对g01和g02函数进行评价时,DEOC算法的收敛方向选择更加精确。在对g04函数进行评价时,DEOC算法在800代左右完成问题优化,速度超过基本DE算法。在对g05、g08和g13函数进行评价时,DEOC算法的收敛精度具有很高的优势,其中g05和g13是含有等式约束的优化问题。相对于基本DE算法,DEOC算法快速找到约束域并且快速向可行域最优点靠拢。所以,DEOC算法是有效的,并且具有更高的鲁棒性和敛速度。 将DEOC算法与SaCDE[14]、新型ICA[15]、PJAD-CDE[16]和MDE+HJ[17]四种约束算法进行比较。其中SaCDE基于双进化策略的差分进化算法,同时对进化种群中较差个体进行改造,使种群的整体目标函数更快速优化。新型ICA将种群个体赋予国家发展思想,通过国内改革和国外殖民的竞争战略思想,使各个小国家向最优解发展。PJAD-CDE采用多种进化策略,并对缩放因子F和变异算子CR进行动态调整。MDE+HJ基于文化基因算法,通过利用变量增量、阶跃缩减因子和终止准则激励最优解进化。表1给出了五种算法的最好值、平均值和方差值。需要注意的是,表1中给出的SaCDE、新型ICA、PJAD-CDE和MDE+HJ算法实验结果由各算法对应文献得到,部分数据由参考文献中数据四舍五入得到,其中:SaCDE最大评估次数为500 000次。新型ICA和PJAD-CDE算法最大评估次数均为240 000次。MDE+HJ算法的最大评估次数为125 000次。 表1 算法运行结果比较 续表1 观察表1统计值,相对于SaCDE和新型ICA,DEOC在最好值、平均值和方差都表现出较高的优势,尤其在g07、g09、g12测试函数的方差值,DEOC明显优于其他两种算法,表明DEOC具有较高的鲁棒性;在最好值的搜索中,除g11逊色于SaCDE和新型ICA外,DEOC在其余测试函数中的最好值均达到最优解。相对于PJAD-CDE算法,在对g13函数实验时,DEOC算法相比于PJAD-CDE算法表现较差,但两种算法在对其余函数求解时,最好解和平均值均取得很好的成绩,并且DEOC算法在g02、g04、g07、g09和g10的方差表现出色,所以DEOC算法与PJAD-CDE算法不相上下并且具有较高的稳定性。在与MED+HJ算法进行比较时,DEOC算法在对g01、g03、g05、g11和g13问题优化结果明显优秀,并且根据问题的特性,可以认为DEOC算法在处理含有等式的约束优化问题时,效果优异于MED+HJ算法。因此,DEOC算法具有较高的收敛精度和稳定性,并且该算法是有效的。 蜗轮蜗杆减速器可以多齿啮合、传动稳定,并且具有良好的自锁能力,所以在机械传动中应用广泛,为保证减速器具有良好的减磨抗振性能,蜗轮常用铸锡青铜和铸铝青铜等贵重的软质材料,提高减速器的柔性。通过优化蜗轮蜗杆参数,可以有效地减小蜗轮齿圈体积,减少贵重金属的使用量,以达到减少成本的效果。本文以某电梯拽引机的普通圆柱蜗轮蜗杆减速器的蜗轮齿圈体积为优化对象,图4给出蜗轮的二维模型示意图,已知P1=7 kW,n1=1 400 r/min,i=20,K=1.2,[σH]=220 Mpa,蜗轮加工材料为铸锡青铜ZCuSn10Pb1。在满足表面接触疲劳强度和刚度的条件下,利用DEOC对蜗轮齿圈进行优化,根据目标函数和约束条件建立式(9)-式(11)的优化数学模型。其中式(11)为参数的取值,且[z1,m,q]=[x1,x2,x3],z1为蜗杆头数,m为蜗轮模数,q为蜗杆的直径系数。优化结果如表2所示。 minf(X)=V(z1,q,m)= (9) L′3-[y]≤0 (10) 式中:E为弹性模量;I为蜗杆截面的惯性矩。 2≤x1≤4,3≤x2≤5,5≤x3≤16 (11) 可以看出,基于DEOC优化的蜗轮齿圈体积约是常规设计方法的51.10%,对优化后的结果进行圆整处理,圆整体积约是常规设计方法的70.34%,因此,DEOC优化方法大大降低了贵重金属的成本支出。 焊接梁的成本计算问题是验证约束算法有效性的常用模型,图5是焊接梁的三维模型示意图,根据文献[18],得到焊接梁成本问题的目标函数式(12)和约束函数式(13),基于DEOC算法对该模型进行优化,并与其他两种先进的约束优化算法MOCoDE[19]和CPSO[20]进行对比,对比结果如表3所示。 minf(X) = 1.104 71x12x2+ 0.048 11x3x4(14.0+x2) (12) s.t.g1(X)=τ(X)-τmax≤0g2(X)=σ(X)-σmax≤0g3(X)=x1-x4≤0g4(X)=0.104 71x12+0.048 11x3x4· (14.0 +x22)-5.0≤0g5(X)=0.125-x1≤0g6(X)=δ(X)-δmax≤0g7(X)=P-Pc(X)≤0 (13) 可以看出,在对焊接梁成本的优化中,DEOC优化结果的最小值、平均值和最大值均为当前所得的最优解,在最大值和方差比较中均优于其他两种算法,表明本文提出的约束差分进化算法DEOC具有更好的实际工程应用效果。 本文提出一种基于反向学习和可行性准则交叉的约束差分进化算法,采用反向学习对种群初始化和边界选择进行处理,有效地提升种群多样性,同时在Deb准则中加入可行性判断条件,对满足可行性准则的个体再次进行交叉处理,可行解进行二次开发利用,提高算法的收敛速度和稳定性。将改进算法应用于蜗轮齿圈和焊接梁优化问题中,显示出DEOC算法在实际工程中应用的有效性。2 改进的约束差分进化算法
2.1 基于反向学习的种群初始化
2.2 基于反向学习的边界处理
3 可行性准则交叉算子
4 实验验证与工程应用
4.1 与基本的DE算法DE/rand/1进行比较
4.2 与其他改进约束算法比较
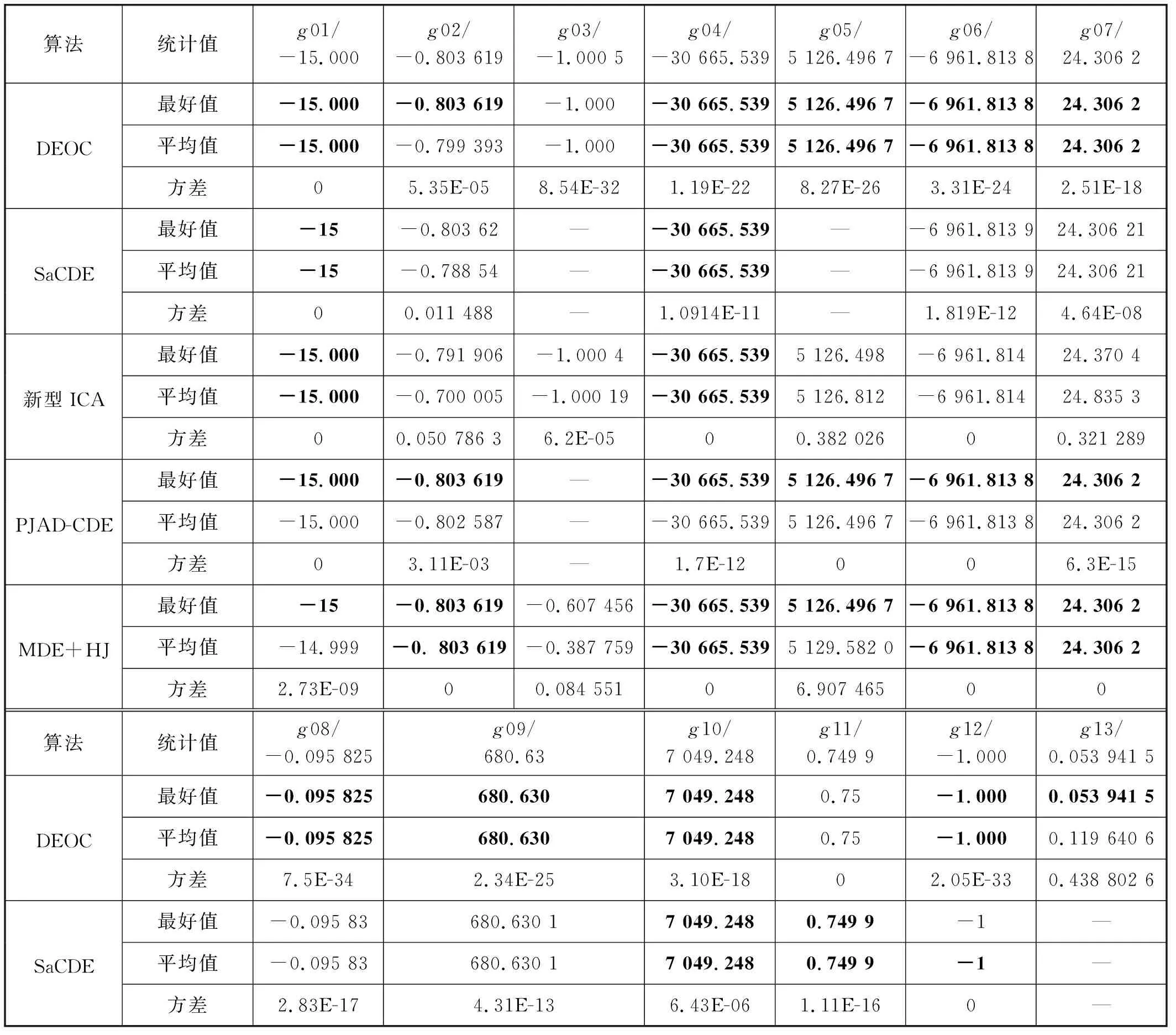
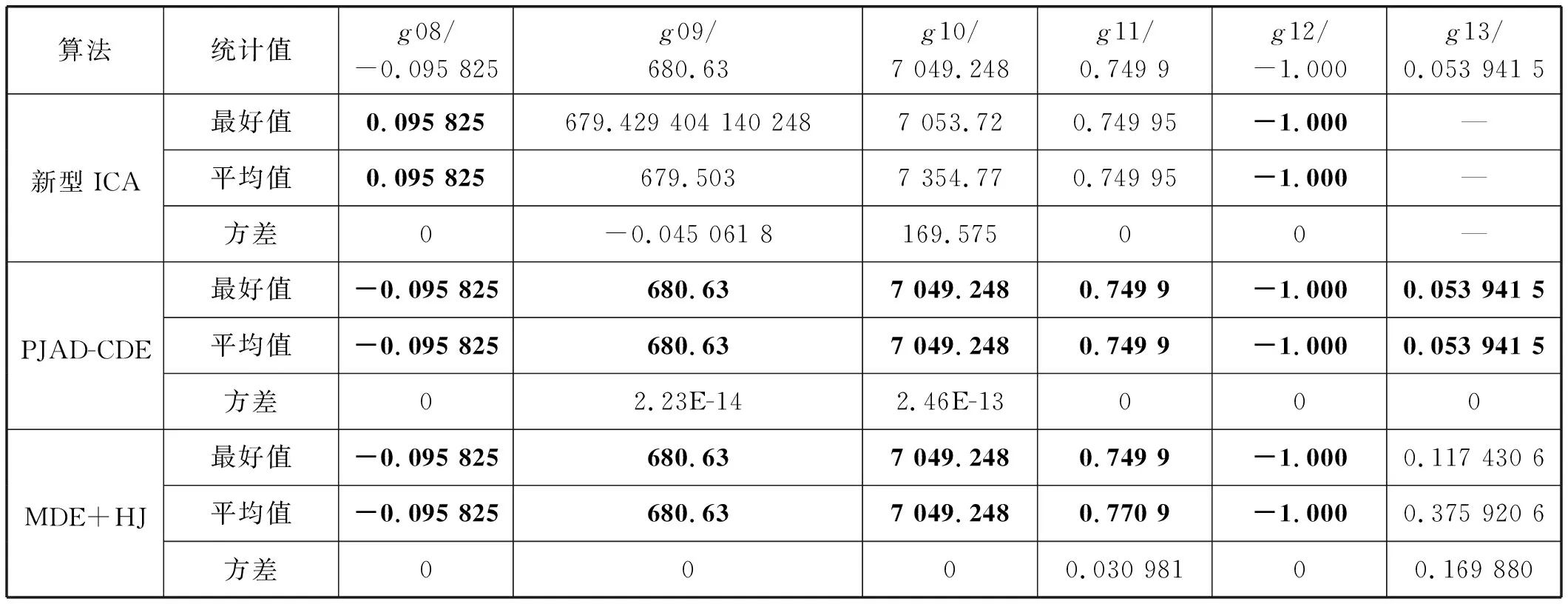
4.3 蜗轮齿圈优化
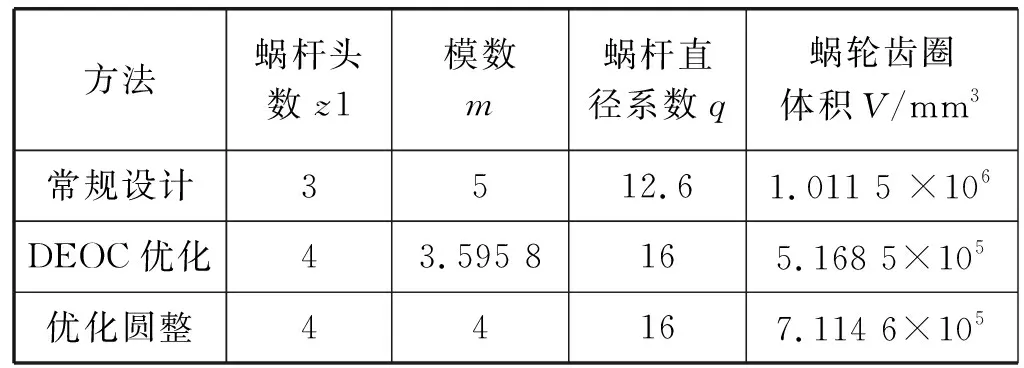
4.4 焊接梁优化

5 结 语

