众包模式参与下“最后一公里”协同配送研究

王 爽 陈淮莉

(上海海事大学物流科学与工程研究院 上海 201306)

0 引 言

物流“最后一公里”的配送在物流领域具有举足轻重的位置，其占据物流总配送成本的30%～50%，促使物流企业不断创新来增强其竞争力。过去几十年智能设备的进步催化出共享经济的新模式，共享经济使得闲置的自然资源成为财富，加之物流行业自身的驱动因素，利用共享经济降低物流成本、提高配送效率成为物流业革新的方向。其中沃尔玛和亚马逊首先提出“众包物流”的理念，使得普通人而不仅仅是物流公司雇佣的员工，可以协同物流公司进行配送。近些年来电商的迅速发展给物流的配送领域带来了新的机遇和挑战，电商的快速发展给物流行业带来了繁荣，同时电商客户众多，订单时间地点分布不均以及运能的不稳定给物流的最后一公里配送带来了巨大挑战。

“兼职员工”在制造业或者商品销售领域应用较为广泛,大量企业通过雇佣兼职员工来降低企业的运营成本。在物流行业，兼职员工主要集中在集散中心，配送领域很少会涉及兼职配送，主要原因在于技术的限制,但是随着电子技术的发展，打破了以前技术的界限，兼职配送成为了可能。

车辆路径问题又称之为VRP问题，在物流领域被广泛研究，VRP的相关研究每年以6%的趋势实现增长。1964年Clarke和Wright首次提出了车辆调度问题，车辆路径的问题研究涉及到经典VRP问题、带时间窗的VRP问题、带有拾货拣货VRP问题，以及以保护环境为主题的GVRP问题。其中Andelmin等[1]通过启发式局部搜索算法，利用多重构图重构解决了绿色车辆的路径问题。Goeke等[2]提出常规车辆以及电动车混合配送问题，研究在城市中如何通过电动汽车和普通车辆的混合配送来节约运输成本。

众包理念来源于共享经济，随着科技进步，电子设备不断更新，解决了众包的技术问题，给众包物流提供了一个有效的平台，学者们对于合作共享的研究也深入到各行各业。Roshanaei等[3]研究了医疗领域的联合手术室排程计划，将医院进行联盟，医生服务于不同的医院，借此来解决医疗资源分配不均的问题，进一步提高医疗资源的利用率。范厚明等[4]针对生鲜品配送提出了多中心联合配送半开放式的车辆路径研究，快速对客户需求做出响应，提高了生鲜品的配送效率，降低了损失率，从而降低了企业成本，进一步促进了生鲜行业的发展。陈萍等[5]针对外卖配送问题提出了基于时间满意度的O2O外卖配送路径优化研究，引入了顾客的时间满意度函数，求解客户的最大满意度。

对于众包物流参与最后一公里配送问题 ，目前国内外的科学研究还比较缺乏，研究与实践不足以支持当前的需求。其中Archetti等[6]提出采用众包车辆参与配送的研究，但是没有考虑送货的时间窗问题，有很强的局限性。Dahle等[7]研究了带时间窗的众包司机的提货和交货问题，提出了不同补偿方案对于配送效率和顾客满意度的影响。Hla等[8]研究了针对驾驶员行为控制的物流公司人员和众包配送员的配送研究，引入了速度等级，通过控制速度，进一步降低成本，降低排放。国内目前研究集中在众包模式理论研究上，鲜少有关于物流公司和众包车辆的联合配送的研究文章。

上述对于物流公司和众包车辆的联合配送研究中，在计算成本时，很少有文献考虑到物流公司员工的启动成本，即物流公司配送员工工资问题,以及对众包车辆接单范围研究过少，没有考虑到众包司机只有在满足一定的距离范围才愿意进行订单的配送。对此，本文将众包车辆接单范围及众包车辆目的地引入到本次研究中，通过研究物流公司和众包车辆的联合配送，减少物流公司配送人员的数量，提高物流配送资源的利用率，实现对物流配送的新的规划。

1 问题描述及模型建立

本文所研究的问题简称为VRPOD问题,可描述如下：某物流配送网络有m个取货点，集合对应为I,I={1,2,…，m},对应n个客户，集合对应为J,J={m+1，m+2，…，m+n}。我们定义从i点配送到点m+i，V是所有点的集合，V=I∪J,0点为物流公司车辆出发点，物流公司车辆记作KR，随机分布的众包车辆记作KO，k∈K=KR∪KO,众包车辆的原始位置记做o(K),众包车辆的目的地为d(k)，客户需求的时间窗记作(ETi，LTi)，lTi表示在客户接受范围内最晚送达时间。边集合E={(i,j)|i,j∈V},长度为dij，物流公司的配送成本由配送员配送的启动成本(即配送员工资)和配送费用组成，从i到j的配送成本记作Oijk，k∈KR，车辆到达时间为Tik，k∈K，K=KR∪KO,服务时间为tik，车辆容量为Qq，q=A,B,C，q=A代表物流公司配送车辆容量，q=B,C时，为众包配送车辆容量，代表三种不同的类型车辆。lik表示车辆k在i节点的载重，dj表示j点的需求量，当dj大于等于0。本文规定众包车辆尽可能多配送订单，物流公司配送车辆要从配送中心出发完成配送后返回配送中心，物流公司的每一辆车可以在时间窗不冲突的条件下完成多个订单的配送。当选择众包车辆配送时，需要满足众包车辆的目的地位置d(K)到配送点J的位置d(jk)<ε(ε为常数)，众包车辆才拥有配送资格。βijk表示订单是否可以通过众包车辆从i配送到达j，wijk表示众包车辆k是否去配送订单;λ是众包车辆的报酬系数,为一个常数;C为物流公司配送员工资，为一个常数。我们规定众包车辆只能配送一单，并且每个订单通过众包配送成本会低于通过物流公司配送。考虑到众包物流的参与以及物流配送过程中会受到天气环境以及配送人员对于路况的熟悉程度的影响从而导致订单配送超时情况,引入客户满意度成本,最后一公里配送中客户的满意度主要与配送的时效性有关，所以通过配送的时效性来代表客户满意度。客户满意度成本主要由两部分构成,G(i)为客户满意度成本系数,b为一个常数。根据上述参数建立数学模型如下:

(1)

(2)

(3)

(4)

(5)

(6)

ωijk≤βijki∈I,j∈J,k∈Ko

(7)

(8)

(9)

Tik+tt,n+i≤Tn+i,kk∈K,i∈J

(10)

(lik+Lj-ljk)xijk=0

i∈V,i∈J,k∈KR

(11)

Li≤lik≤Qqi∈V,k∈K

(12)

xijk={0,1}

(13)

βijk={0,1}

(14)

ωijk={0,1}

(15)

目标式(1)表示总费用最小，费用包括物流公司配送员的工资，配送的运输成本和对众包司机的报酬三部分组成。约束条件中：式(2)限制物流公司配送车辆从配送中心出发。式(3)限制物流公司配送车辆完成配送任务最后返回配送中心。式(4)表示是否通过物流公司配送。式(5)表示物流运输的平衡关系。式(6)表示众包车辆是否拥有配送资格。式(7)表示拥有配送资格的众包司机是否决定配送订单。式(8)表示每一个订单只能通过一次配送。式(9)表示客户满意度系数与配送时间的关系。式(10)表示订单配送的先后顺序。式(11)表示物流公司配送车辆容量限制。式(12)表示配送的重量不能超过配车辆的最大容量。式(13)-式(15)表示变量取值为0-1变量。

2 算法及求解

由于考虑众包模式的车辆路径问题比较复杂，精确算法往往很难在短时间内得到精确求解。国内采用的大多数均为启发式算法和混合式启发式算法，考虑到VRPOD问题中相比经典VRP问题多考虑了众包司机这一因素，并且对众包司机配送条件加以限制，考虑因素众多，算法的求解效率和降低成本都很重要。采用基于聚类分析的遗传算法进行求解。第一步先进行聚类分析得出众包司机配送的订单，本文假设采用众包物流配送一个订单的配送成本是低于通过物流公司的配送成本的，通过聚类分析得出能够通过众包配送的最大订单量；第二步对物流公司配送的订单进行遗传算法求解。

2.1 “订单-目的地”配对策略

将要配送的订单位置与众包车辆目的地按照经纬度进行配对。例如订单i对应的“订单-目的地”按照配送订单经纬度位置，众包车辆目的地经纬度位置进行配对。

2.2 聚类过程

K-means算法是最经典、应用最广泛的聚类分析方法，其目标是使得类内距离尽可能小，类间距离尽可能大。本文采用K-means算法对“订单-目的地”进行聚类，聚类的数目即为采用众包车辆配送的最大数目。由于待聚类对象的维度一致，且费用与距离呈现正相关性，无需加权，且配送属于距离配送，因此在聚类中采用欧氏距离进行聚类，成本函数表示为类内距离平方和与类间距离平方和之比：

(16)

式中：D=1,2，3,4表示的是订单位置和顾客目的地的四个经纬度集合；vji表示j的第i维，cl表示离对象j最近的类中心；cli表示cl集第i维的值；Ψlj表示对象j是否属于类l，是为1，否为0。

聚类算法步骤如下：

Step1初始化聚类数目k=λ0(λ0=max{符合众包配送条件约束的临时车辆数，当前需要配送的订单数})。

Step2初始化k个聚类中心。

Step3计算每个对象j到每个聚类中心cl的距离，将每个对象赋予距离最近的类。

(17)

Step4计算各类cl中所包含的对象ψlj的总和，从每一个类挑出距离最近的一个对象，把其他对象赋予距离次近的类，同时调整ψlj值。综上，可以得出最大临时车辆的配送情况，且k的值会随临时车辆数量的变化而发生变化。该算法把每一类看作一辆众包配送车辆，类中涉及的订单由此辆众包车辆来完成配送。

2.3 传统配送方式的路径优化策略

Step1染色体编码。对于通过物流公司配送的订单，我们规定一个客户只能被一辆车服务，所以染色体中的客户不存在重复的客户点。如果一个客户存在多个订单我们模拟为多个客户，根据车辆行驶顺序编码的形式进行编码,用(G1,G2,，…，Gn+k)表示染色体,Gi=0表示配送中心,k代表目前存在的车辆数量,假如目前有三辆车进行订单配送,行驶路径为{(1,2)(3,4,5,6)}若目前有固定车辆和满足条件的临时配送车辆一共五辆车,则编码为(1,2,0,3,4,5,6,0,7,0,0,0)。

Step2初始种群的形成。我们采用随机生成的方法形成初始种群,随机产生M条可行解路径,每条路径均为一条染色体,M条染色体可以构成一个种群规模为M的初始种群,然后以这个初始种群进行迭代。初始解的质量的优劣直接影响搜索的速度和质量，所以初始解的质量也很重要。

Step3计算适应度函数。我们以本文的优化目标作为适应度函数，以路径{3,4,5,6}为例，适应度函数T=C+c34d34+c45d45+c56d56+c60+d60，适应度函数为成本函数，计算每条路径的成本函数,即为本次路径的适应度。

Step4进化操作。进化操作包括交叉、变异、选择，从适应度数值中选择出比较适合环境的个体。

2.4 算例分析

根据本文的研究思路以及模型的特点，给出相应的参数设置，并且利用MATLAB进行求解，验证模型的正确性。我们假设订单配送时间在[0，60]的区间之间，即模拟一小时的订单配送情况。

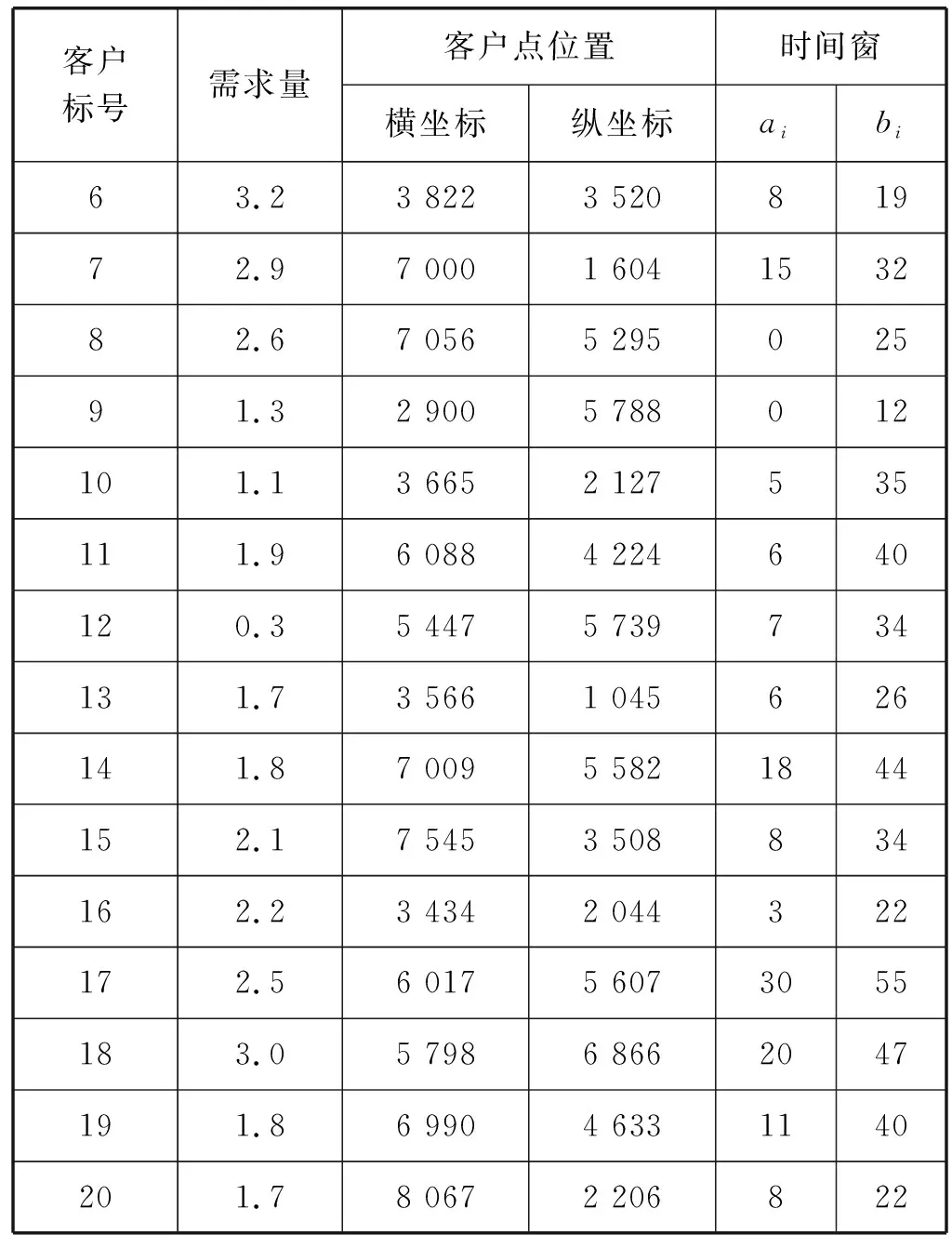
通过用MATLAB随机分别生成20个客户位置信息和10、20个随机车辆位置信息，首先采用传统配送方案,即订单完全通过物流公司进行配送。对于这种情况本文采用遗传算法进行路径规划；其次分别假设存在10辆和20辆众包车辆，并且众包车辆参与配送。由于订单配送情况是动态的,影响订单配送的因素也是事先无法预测的,为了验证模型的准确性,采用MATLAB生成随机数生成程序随机产生订单延迟配送情况。由于在现实中除特定节假日订单配送的准确性很高，因此假设订单延迟配送的概率为0.05%，其中在顾客接受的配送时限延迟配送概率为0.03%，在顾客接受范围之外的延迟配送概率为0.02%。随机生成的客户位置如表1所示，众包车辆情况如图1和图2所示，众包车辆类型及容量限制如表2-表4所示，相关参数设置如表5所示。

表1 客户分布情况

续表1

表2 众包车辆基本情况(车辆数目为10)

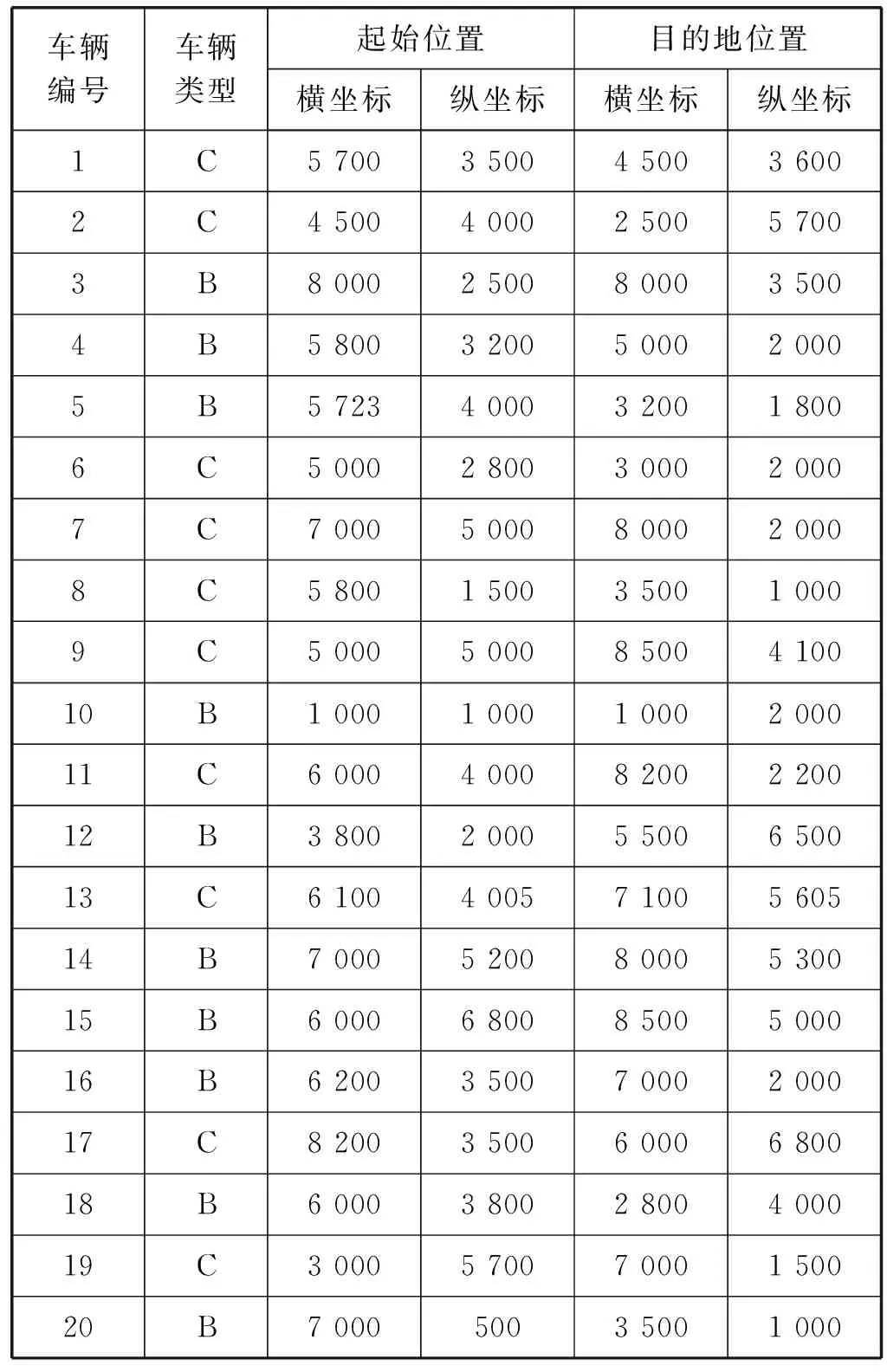
表3 众包车辆基本情况(车辆数目为20)

表4 车辆容量分布

表5 测试集参数设置

首先不考虑众包配送的情况，则问题简化为传统配送问题采用遗传算法求解，求解的最优配送如图3和表6所示。

表6 传统配送最优路径

然后采用物流公司和众包车辆相结合的配送方式，先对客户进行聚类分析。聚类原则为尽可能采用众包车辆配送，众包司机每次仅配送一单，根据众包车辆目的地位置及订单位置，在满足众包车辆配送的条件下采用行驶距离最少原则进行聚类分析。聚类结果如表7、表8所示。

表7 当众包车辆为10时

表8 当众包车辆为20时

对传统车辆配送通过遗传算法求解，当众包车辆数目为10时(方案1)，配送路线如图4所示，最优略径如表9所示，众包车辆配送信息如表10所示。

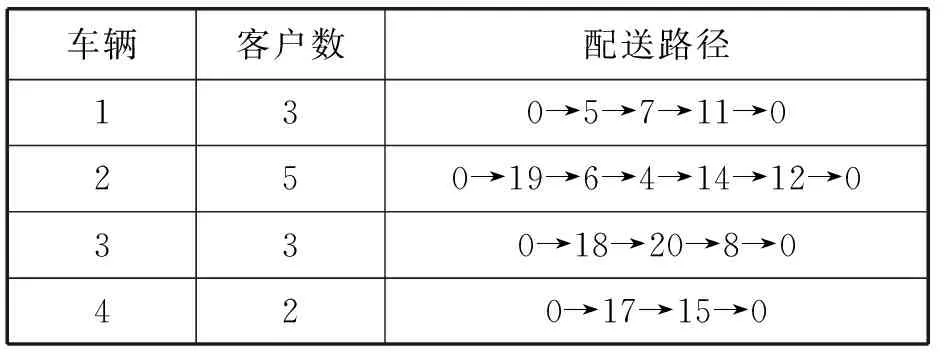
表9 方案1最优路径

表10 方案1众包车辆配送信息

当众包车辆数目为20时(方案2)，配送路线如图5所示，最优路径如表11所示，众包车辆配送信息如表12所示。

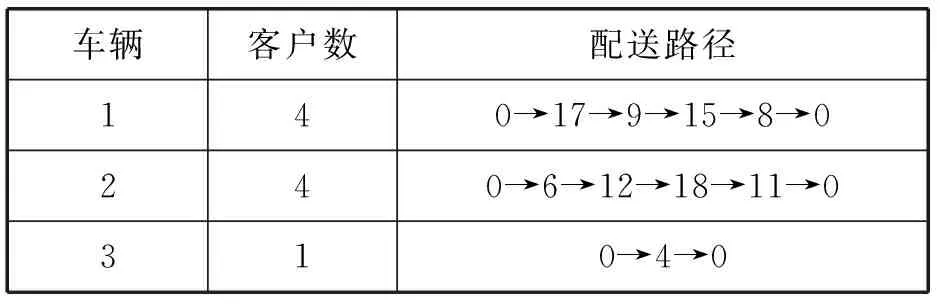
表11 方案2最优路径

根据MATLAB随机生成的数据得到采用传统配送延迟配送的配送点为点8，延迟配送的户满意度成本为5元，采用10辆众包车辆参与配送的延迟配送点为点9，延迟成本为10元，采用20辆众包车辆参与配送的延迟配送点为点1和点7延迟成本分别为15元和3元。两种配送成本比较如表13所示。

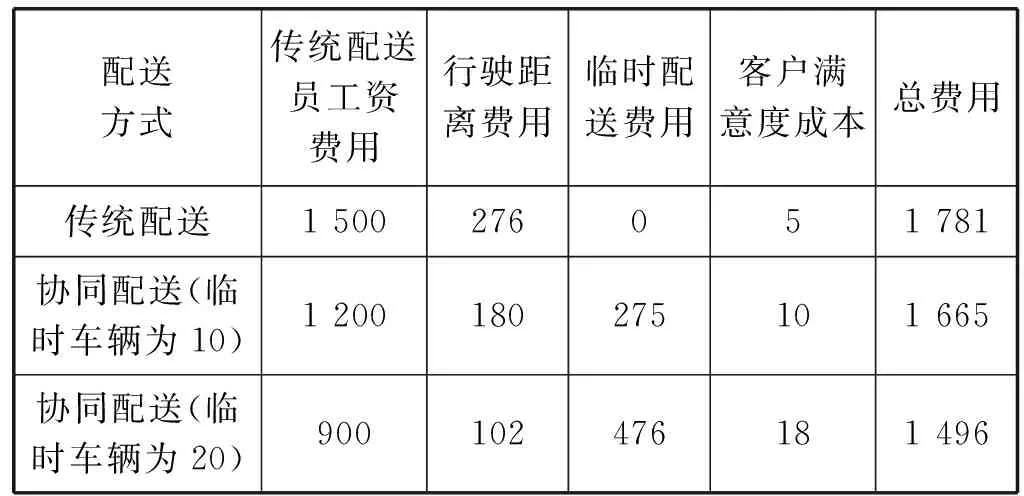
表13 配送成本比较

3 结 语

由上述案例可知，众包配送的引入可以降低物流的运输成本，众包车辆参与配送的数目越多，成本降低得越多，众包参与最后一公里配送能够在一定限度上节约配送成本。且众包车辆参与配送能够在原有基础上增加配送能力，减少物流公司配送车辆的数量，在同等订单需求下，众包车辆参与配送能够以更便捷的速度更低廉的成本达到配送需求，可以更好解决物流特定节假日产生的大量订单需求。

针对目前物流配送运能不均的现状和物流资源不能合理利用的问题，引入众包物流的概念，可以在一定限度上解决上述问题，同时可以进一步使得闲置资源得到最大化的利用，进一步解决了物流资源不够充分的问题，降低运输成本，提高资源的利用率，为目前配送问题提出了切实可行的解决方案,并且为企业节约运输成本。众包车辆参与配送主要与其目的地和报酬率有一定的关系，不同的报酬率可能会造成不同的影响，这是一个值得进一步探讨的问题。本文只考虑一个众包车辆只配送一个订单，没有考虑一个众包车辆配送多单的情况，也没有考虑随机订单的情况，使得本文有一定的局限性。