基于局部邻域标准化和核主元分析的故障检测

曾 静 李 磊 李 元

(沈阳化工大学信息工程学院 辽宁 沈阳 110142)

0 引 言

随着现代工业的发展，大多工业产品的生产要经过多道工序才能完成，因此针对多阶段生产过程中的异常检测也成为了研究的热点。为了充分利用工业生产中收集的海量数据，基于数据驱动的多元统计监控(Multivariate Statistical Process Monitoring，MSPM)技术已在工业过程中得到广泛应用[1]。

在过程故障检测中主成分分析(PCA)、偏最小二乘(Partial Least Square, PLS)的应用最为广泛，但是这两种方法中的监控指标T2和SPE都是在过程数据满足多元高斯分布的前提下提出的，这使得PCA和PLS在对多模态故障数据进行检测时会出现很高的漏报率。另外，PCA是一种线性降维方法，因此其忽略了数据本身包含的非线性特征。针对非线性问题，核主成分分析(KPCA)方法被引入到过程监控中[2]。KPCA使用一个未知的非线性映射φ(·)将低维空间数据变换到高维度空间中，再进行主成分分析[3]。与传统的PCA相比，KPCA具有主成分特征明显、贡献率集中等优点，其性能优于PCA[4]。由于KPCA同样采用T2和SPE作为监控指标，因此在处理多模态数据时依然存在不足。

对于多模态数据Ma等[5-6]提出了局部邻域标准化(LNS)策略故障检测方法，在使用数据进行建模之前需要对数据进行预处理。数据预处理方式大多使用Z-score方法，该方法将不同量纲下的数据归一化成均值为0方差为1的数据，从而避免了数据量纲的差异给故障检测带来影响。但是Z-score方法并没有改变数据原来的分布特征，例如预处理之前的数据是多模态的数据，那么经过Z-score方法处理后的数据还是多模态数据，而LNS方法使用样本的局部邻域集合的均值和标准差对样本进行标准化处理[7]，不仅能将各个模态的数据中心平移到原点，还能调整各阶段的离散程度使之近似相同，提高了方差不同的多阶段过程故障检测能力。经过LNS方法处理后的多模态数据变成近似服从单一的多元高斯分布的单模态数据。

针对过程监控中数据的多模态和非线性问题，本文提出一种使用局部邻域标准化和KPCA相结合的故障检测(LNS-KPCA)方法。首先使用样本局部邻域集合的均值和标准差对样本进行标准化，使各个模态的数据中心平移到原点，从而消除数据的多模态特征，利用KPCA对标准化后的数据进行建模和故障检测。LNS-KPCA可以将多模态数据融合为单模态数据，还继承了KPCA处理非线性数据的能力，可以有效地对多模态和非线性过程进行监控。

1 核主成分分析

设采集到l个样本每个样本有N个观测变量，则得到的数据集可表示为X={x1,x2,…,xl}，xk∈RN，通过非线性映射函数φ(·)将原始数据集X映射到高维特征空间G中，则G中的样本可记为φ(xk)，φ(xk)的协方差矩阵C为:

(1)

C的特征值λ和特征向量V表示为:

λV=CV

(2)

对应的特征向量V可由G空间中的样本映射形成:

(3)

式中：φ(X)=[φ(x1)φ(x2) …φ(xl);];α=[α1α2…αl]T。

此处引入核函数：

Kij=K(xi,xj)=〈φ(xi),φ(xj)〉i,j=1,2,…,l

(4)

问题从求取高维空间中协方差矩阵的特征值和特征向量转变成了求核矩阵的特征值和特征向量，即：

lλKα=KKα⟹lλα=Kα

(5)

归一化特征向量V，则样本φ(xk)在V上的映射为:

(6)

(7)

E越大则前m个较大的特征值对应的特征向量组成的矩阵就越能拟合原始空间数据。

(8)

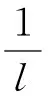
T2统计量为主元得分，表示为:

T2=[p1,p2,…,pm]Λ-1[p1,p2,…,pm]T

(9)

式中：Λ-1是对应特征值λk的倒数。T2的控制限为：

(10)

Q统计量定义为：

(11)

控制限可由式(12)求得:

(12)

式中：g和h是训练样本的SPE指标的均值和方差;α为置信度。

2 基于LNS-KPCA的故障检测方法

KPCA相对于PCA在发掘数据的非线性特征方面有其独到的优势，但是KPCA使用的故障检测指标T2和SPE都是在数据满足单一高斯分布的前提下提出的，而实际的工业过程生产大多是多工况、多阶段的生产方式，因此数据大多是多模态分布的，并不满足单一高斯分布假设。针对KPCA在处理多模态数据上的短板，本文利用了LNS方法来融合多模态数据，使其近似服从多元高斯分布。

在使用数据进行建模前都要进行数据的预处理，目的是消除不同测量变量之间量纲的差异给后续的故障诊断带来干扰。LNS方法首先在原始数据集X中寻找每个样本Xi的前K个邻域集合n(Xi)，然后计算该邻域集合的均值mean(n(Xi))和标准差std(n(Xi))，最后利用式(13)对Xi进行规范化处理。

(13)

经过上述步骤的数据预处理后，使得不同模态数据的中心被平移到原点，消除了数据的多模态特征，弥补了KPCA在处理多模态数据方面的不足，为后续的研究奠定了良好的基础。

2.1 模型建立

(1) 采集正常工况数据作为训练数据集X。

(2) 在训练集X中寻找每个样本的前K个邻域集合n(Xi)，利用式(13)对该样本进行标准化处理。

(3) 利用式(3)-式(6)求出原始数据在高维特征空间中特征值特征向量，应用式(7)确定主元个数。

(4) 利用式(9)和式(11)计算T2和SPE统计量。

2.2 在线检测

(1) 将生产过程中测得的数据作为待检测样本，在训练集X中寻找该样本的前K个邻域集合n(Xi)。

(2) 利用式(13)对该样本进行标准化处理。

(3) 根据式(9)和式(11)计算T2和SPE统计量。

3 仿真实验

3.1 数值例子

该非线性数值例子是由s1和s2构成的七变量数据组成[10]，表示为：

(14)

式中：e1-e7为服从N(0,0.01)的噪声；s1是-10到-7之间的随机数，本例中s2取两种正态分布的数值，以产生两种模态数据。

Modal1s2：N(-15,2)

Modal2s2：N(5,0.5)

针对上述两种模态，分别生成500个样本，共计1 000个样本组成训练数据集。测试数据集共包括500个样本，设计故障情况如下：故障1按照模态1来运行，从第251个样本开始在变量x1上引入幅值为0.6的阶跃故障。故障2按照模态2来运行，从第251个样本开始在变量x7上引入幅值为0.04(k-250)的斜坡故障，其中k为采样时刻数。

针对上述故障分别使用KNN、PCA、KPCA和LNS-KPCA对其进行故障检测。通过寻优测试确定KNN方法中K取30，根据累计贡献率法，PCA、KPCA方法中主元个数取2，LNS-KPCA方法中K取30，主元个数取3，其中KPCA和LNS-KPCA均采用高斯径向核函数，核参数均为700，均采用95%的控制限对故障进行监控。

四种方法的检测结果如图1-图4所示。从图1的D2统计量可以明显看出数据分为两个模态，且前一个模态在计算统计控制限时占主导作用，对故障的检测效果很不理想。由于PCA、KPCA均采用T2和SPE作为监控指标，对于本例中的多模态数据，并不满足数据单一分布的假设，从图2和图3中可以看出两种方法的检测效果也并不理想。为了弥补KPCA在这一方面的不足，本文利用LNS能够消除数据的多模态特征这一优点。从图4可以看出将其与KPCA相结合后检测效果得到了大幅度提高，为了使数据可视化取训练数据和故障数据的前三个变量进行作图。从图5可以看出，针对本例中的多模态数据，经过LNS处理后数据从多模态数据变成了单模态的数据，为KPCA处理多模态、非线性数据奠定了良好的基础。

3.2 青霉素发酵过程仿真实验

青霉素发酵过程是一个典型的非线性过程。青霉菌可分为两个阶段:(1) 青霉菌适应生长繁殖阶段，经过短时间的适应后开始迅速生长繁殖，并快速消耗葡萄糖引物;(2) 青霉菌合成青霉素阶段[11-12]。因此青霉素发酵过程数据也是呈现多模态的特征。本文使用PenSim2.0仿真生成青霉素发酵过程数据，可在搅拌功率、通风率和底物流加速率上人为引入阶跃和斜坡两种故障，并且可以进一步设置引入故障的幅值和起止时间[13]。PenSim2.0平台产生的数据共有17个监控变量，详情见表1。

表1 青霉素发酵过程变量名称

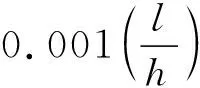
与数值仿真相同，同样采用KNN、PCA、KPCA和LNS-KPCA四种方法对故障进行检测，并进行对比分析。通过寻优测试确定KNN中K取3，由累计贡献率法确定PCA中主元个数取4，KPCA中主元个数取11，核参数取700，LNS-KPCA中K取6，主元个数12，核参数同样取700。以上实验统一采用95%控制限。

4 结 语

对于工业过程数据的多模态和非线性，本文将局部邻域标准化与KPCA相结合。传统的Z-score方法在处理多模态数据时由于使用的全局均值和标准差，忽略了数据的多模态特性。而LNS方法利用样本点的局部邻域集合的均值和标准差对样本进行标准化，能使各个模态的中心点向原点靠拢，从而消除数据的多模态特征。与KPCA相结合可以发掘出隐藏的非线性信息，将之应用于青霉素的发酵过程，结果验证了该方法的有效性。