非线性方程组求解器全局优化求解能力对比研究
程培澄 程培聪 王 萌 邵宇辰 亓路宽
1(北京工业大学材料科学与工程学院 北京 100124) 2(北京交通大学计算机与信息技术学院 北京100044) 3(北京工业大学生命科学与生物工程学院 北京 100124) 4(北京工业大学建筑工程学院 北京 100124)
0 引 言
非线性方程组的求解是科学计算领域里最基本也是最重要问题之一,不论是理工科类还是社会人文科学类,很多问题都最终归结为方程组求解问题。方程组求解一般分解析解和数值解两种类型,能得到解析解自然是最好的结果。但现实中,基于问题的复杂性和目前的技术,很多时候非线性方程组都是无法得到解析解的,此时只能通过数值计算方法得到数值解。当前非线性方程组数值计算最常用的方法有牛顿算法、共轭梯度算法、最速下降法等,这些算法实际上都是一种优化迭代算法,因此方程组数值求解问题也可以视为优化求解问题,式(1)可以转换成等价的优化问题,即求函数最小值问题,式(2)为一标准的无约束函数最小值优化问题。
(1)
(2)
非线性优化问题所涉及到的优化算法一般可分为局部和全局最优算法两种。局部最优算法效率高但对参数初值依赖严重,迭代起始初值的质量好坏决定了计算是否收敛从而得到正确结果,而要猜测给出合理的初值并非易事,基本是运气加经验,对复杂点的优化问题很多时候即使经过多次尝试,计算仍然无法收敛,因此初值依赖症是局部最优算法的最大缺点,前述牛顿算法等均属局部最优算法;相对局部最优算法的则是全局最优算法,其最大特点是不依赖于初值,也即无须再猜测初值,即可获得全局最优解,典型代表算法有遗传算法[1]、模拟退火算法[2]及一大批启发式仿生智能算法如粒子群算法[3]、蚁群算法[4]等。如果仅从上述概念描述来看,全局优化算法相比局部最优算法无疑有巨大的优势,但实际却并非如此。全局优化算法有两大不足,一是计算量大,其寻优特性决定了计算资源的高消耗,虽然硬件能力的提升及并行算法等可以进行一些弥补;二是任何全局最优算法,至少到目前为止也仅是从理论上证明可以不依赖初值而全局收敛,而实际应用当中却与理论相差甚远,很难保证每个优化问题都百分之百收敛到全局最优。
正因为全局最优算法在理论层面完美而实际表现差强人意,存在改进完善的巨大空间,因此国内外众多研究者都投入其中[5]。仅国内看,从同方知网分别以“遗传算法”全文检索并含“优化”以及“优化算法”全文检索并含“全局”关键字进行查询,如图1所示。从2008年至2018年这11年间,以遗传算法或全局优化算法为研究内容的论文数每年平均都上万篇,并呈逐年增加的趋势。在全局优化算法研究中,尤其以启发式智能仿生优化算法最为热门,如粒子群算法、蚁群算法、蛙跳算法、蝙蝠算法、布谷鸟算法、根生算法、鱼群算法等,共有数百种之多,每一种算法的提出者均称该算法相对于其他算法取得了更好的全局优化结果,然而这些算法要么没有编译成通用软件求解器而导致用户无法应用验证,要么用户按介绍自己实现原算法编译求解,但计算结果却远达不到原作者所宣称的效果。同时通过调研了解,国外被众多用户广泛认可的著名通用优化计算平台如GAMS[6]和AMPL[7]等,其内含的数十种知名优化求解器几乎都没有采用上述任何一种智能仿生进化优化算法,著名的数值和符号计算软件MATLAB及Mathematical,在其附带的全局优化工具箱中虽然包含有一些基于上述启发式仿生进化算法如粒子群算法的全局优化求解器,但其实际应用效果远不如专业优化计算的GAMS或AMPL平台所包含的求解器,尤其是全局优化求解器Baron、Antigone、Couenne和Lingo,这4种求解器均已被证明在全局优化求解方面处于世界顶级[8-10],然而遗憾的是国内却少有研究涉及对这些全局优化求解器相对全面的对比研究,因此本次研究选择这4款全局优化求解器,再外加唯一国产优化数值计算软件1stOpt共5款软件作为研究的对比对象,而数学领域应用极广的MATLAB和Mathematical虽然都有现成的非线性方程求解功能,但都是基于局部最优算法的,而其附带的全局优化求解功能与选择的5款专用优化软件相比,不论效果还是易用性方面都有很大的差距,因此不在本次评价之列。
Baron求解器是现任美国卡耐基梅隆大学教授Sahinidis最先于1996年在伊利诺伊大学任教时研发出的全局优化求解器,历经二十余年的持续改进升级,已被公认为当今最先进强大的全局优化求解器[11]。Antigone求解器是美国普林斯顿大学Floudas教授和英国帝国理工学院Misener教授共同研发并于2013年首次发表的优化求解器,专注于连续及整数规划全局求解,业界享有极高的声誉。Couenne求解器是美国COIN-OR公司开发的非线性全局最优化求解器,起源于2006年IBM与卡耐基梅隆大学的一个合作项目,该求解器开源,有多种不同编程语言接口,方便使用。Lingo是美国Lindo公司于1981年开发出的优化计算平台,具有自己的模型语言,使用简单且用户广,世界500强公司中的一半以上都在使用。该软件国内知名度也很高,几乎是国内各种数模竞赛的缺省推荐软件。1stOpt是唯一一款国产通用数值优化计算软件,国内各大高校、科研院所及许多公司都在使用,该软件最大特点就是其特有的UGO全局优化算法以及其易用性,短时间内就赢得了众多用户的认可与推崇[12-13]。
GAMS是通用的优化计算平台,上述四款全局优化求解器Baron、Antigone、Couenne和LingoGlobal均包含在GAMS优化计算平台之中。GAMS提供统一的应用界面和语言,底层调用上述求解器,用户只需掌握GAMS语言而不需分别了解各个求解器的特有语言,极大提升易用性。本次采用的GAMS版本是25.1.3,最新试用版可从GAMS官方网站免费下载;1stOpt使用的版本是8.0。各求解器都有众多的选项设置,不同的设置对计算结果会有一定的影响[8],方便起见本次研究中各求解器均采用适合于大多数情况的缺省设置。
1 非线性方程组研究案例
检验全局优化算法或全局优化求解器的最佳方法就是采用相应的测试题进行实际计算比较。国内不少学者采用典型案例在全局优化算法求解非线性方程组方面进行了不少有益的探索[14-17],此外目前世界上已有不少经典的全局优化测试题集,如著名的GLOBALLib[18]和MINLPLib[19]。然而采用上述已有经典测试题集存在以下三个问题:1) 这些测试题集已被众多相关研究者进行了广泛和深入的研究对比,并在此基础上对优化算法进行了针对性的改进,这有可能会导致这些算法或求解器对这些测试题集产生一定的“免疫”功效,由此导致无法对各种优化求解器进行严谨、客观及公正的测评。2) 这些经典测试题集不少都是五年甚至十多年前提出的,在当时确实具有一定的难度和代表性,是开发检验优化算法的极佳案例,但随着科技的快速发展,这些测试题集中的不少问题对当今优秀的最优化求解器来说已过于简单,获得正解已是非常轻松简单的事,因此也基本失去了其算法测试、验证与挑战的功能。3) 相对于局部优化算法,全局最优算法主要侧重于效果,一般而言计算消耗较大,因此维数低但难度高的问题才是测试验证全局最优化算法的最佳选择,而已有的测试问题要么维数太高导致计算时间太长,不利于对问题的高效验证,要么难度太低而无法有效检验不同优化求解器的优劣。
基于上述分析,本次研究没有选择已有的测试题集,而是采用了作者收集整理或实际应用所遇到的14道非线性方程组问题,均属首次公开发表。这些问题求解规模都不大,求解参数在3到6个之间,属于低维小规模优化求解问题,但求解难度却非常高,比之绝大部分流行的优化测试题集难度要大很多,但正如前述,规模小但求解难度大,这正是验证全局最优化算法或软件求解器的最佳案例。这14道测试题案例分述如下。
案例1:五元非线性方程组。
(3)
式中:n=5,a=[80.003 1,202.536 7,251.145 5,340.013 0,352.013 6],b=[0.55,1.45,1.55,2.75,3.15]。
案例2:四元非线性方程组。
i=1,2,…,n
(4)
式中:n=4,a=[283.15,298.15,313.15,328.15],b=[0.208 7,0.205 9,0.203 4,0.200 8]。
案例3:五元非线性方程组。
x1exp(-x2(ai-x3)2)+x1exp(-x4(ai-x5)2)-
bi=0i=1,2,…,n
(5)
式中:n=5,a=[50.86,25.17,8.53,4.39,3.15],b=[48.24,96.53,274.65,508.44,683.08]。
案例4:六元非线性方程组。
(6)
式中:n=6,a=[9,18,36,54,72,108],b=[1,0.89,0.84,0.78,0.6,0.39]。
案例5:三元非线性方程组。
(7)
式中:n=3,a=[1 990,2 002,2 005],b=[0.22,0.31,0.33]。
案例6:五元非线性方程组。
(8)
案例7:三元非线性方程组。
(9)
案例8:五元非线性方程组。
(10)
式中:c=1.300 5。
案例9:四元非线性方程组。
(11)
式中:n=4,a=[915,909,898,895],b=[1 200,1 212,1 234,1 240],c=[1.6,3.54,5.43,5.683]。
案例10:六元非线性方程组。
(12)
案例11:三元非线性方程组。
(13)
案例12:六元非线性方程组。
(14)
案例13:三元非线性方程组。
(15)
式中:b0=0.029 2,b1=6.17,b2=7.86,u=5 028。
案例14:四元非线性方程组。
ai=x1(1-exp(x2bi))+x3(exp(x4ci)-1)
i=1,2,…,n
(16)
式中:n=4,a=[3.8,27.9,23.5,13.7],b=[8.2,63,59.5,35.7],c=[8.1,35.667,59.5,35.7]。
2 优化求解器测试对比
2.1 测试环境及设定
所有非线性方程求解案例问题均转换成如式(2)的最小值优化问题。Baron、Antigone、Couenne和Lingo Global四个求解器均在GAMS平台执行,除了求解器选择不同,其他代码均相同;1stOpt采用其独立的桌面平台实现。每个求解器均采用缺省设置,系统运行环境及硬件配置相同;对每个测试题都独立运行10次;对不同的求解器结果评估时,如果具体参数值基本一样而目标函数值虽都趋近于0,但比值相差较大,仍视为结果相同,如案例4中Couenne与1stOpt,二者目标函数值分别为5.12495E-7和7.482169E-14,比值相差巨大但都趋近于0,而且参数组具体值基本一样,因此视为相同结果。
测试指标主要有两个:一是目标函数值,对解方程问题而言,获得正解时的目标函数值理论上应该为0,实际数值计算中一般为趋近于0;二是计算时间。这两个指标也分别代表效果和效率,是判断一个优化求解器好坏的两个最重要指标。
2.2 测试结果
对于优化计算而言,非线性方程组的目标函数是非常复杂和高度非线性的,图2和图3是典型的两个示意图。图2展示最优点位于整体梯度平缓的“深井”之中,而图3则是在“起伏山坡的密林”之中搜索最低点,全局求解难度非常大。详细计算结果见表1及表2。

表1 案例1-案例7测试结果

续表1

表2 案例8-案例14测试结果
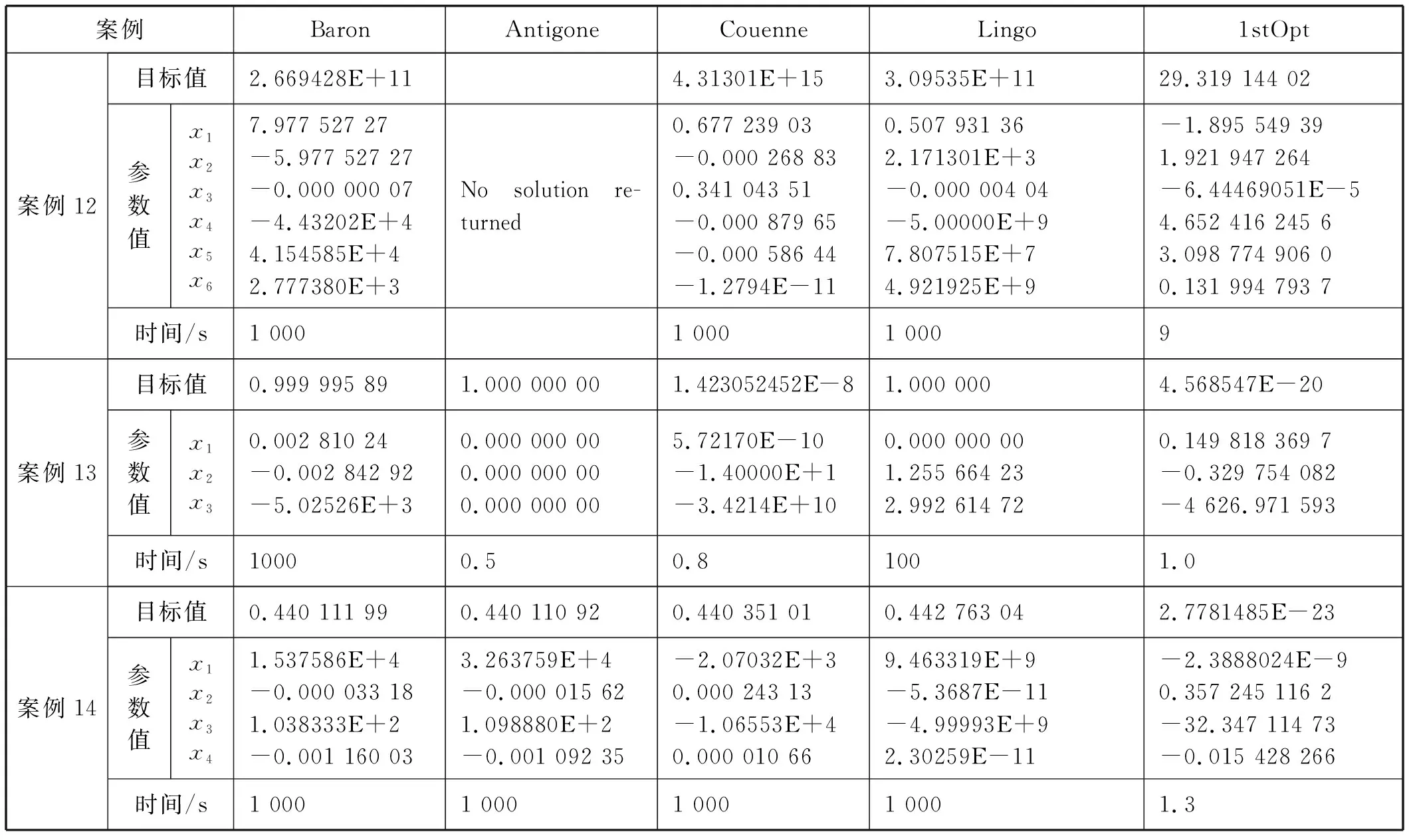
续表2
案例1,它是一个方程形式完全一样的四元四次方程组,1stOpt能以超过90%的概率得到最优解,且用时短;其他求解器均只能获得局部最优解,同时计算时间很长。
案例2,虽然从目标函数值看五种求解器的结果均趋近于零,但只有1stOpt结果精度最高且稳定,其余四种求解器所得参数结果千差万别。
案例3,Antigone和1stOpt均取得了相同的正解,Antigone用时较长,是1stOpt的7倍之多,其他三个求解器的结果与目标函数值为0的理论正解相比,误差巨大。
案例4,求解难度较大,1stOpt能以约50%的概率求得正解,Baron、Antigone和Lingo结果与正解相差甚远,反而是开源的Couenne表现最为出色,几乎能以百分之百概率得到正解,令人惊叹。
案例5,虽然只有三个未知参数,但想得到最优解却十分不易。Baron很快能得出结果,但却是错误的;Antigone和Couenne计算时间很长但最终结果也不对;1stOpt能以40%的概率得到最优解;Lingo结果从目标函数值看相对Baron、Antigone和Couenne好一些,但具体参数值与1stOpt的相比,明显也只是一个局部最优解。
案例6,Antigone和1stOpt都可以很快得出正确结果,二者目标函数值虽然有较大差距,但应该是参数取值精度引起的。Lingo目标函数值虽然也较小,但具体参数值与最优解相比完全不对;Baron和Couenne耗时长但计算结果也不对,仅是局部最优解。
案例7,虽然只有三个未知参数,所有5个求解器,不论计算时间长短,所得结果基本一致,但可判断都不是目标函数趋近于0的正解,难道该方程本身就无解?
案例8,Lingo和1stOpt都可求出正解,但前者耗时较长;Antigone、Baron和Couenne所得结果误差很大。
案例9,1stOpt结果最好且稳定唯一,其余求解器虽然目标函数都趋近于0,但具体参数值差别巨大,应该均为局部最优解。
案例10,所有求解器的结果都差强人意,从目标函数值看Baron结果最好,1stOpt的结果次之,但有的参数值达到了1E+305的数量级,令人困惑;其他三个求解器结果均与理想值0相差甚远。难道该方程组也无精确解?
案例11,Baron、Lingo和1stOpt均可获得正解,Antigone和Couenne结果仅为局部最优且与正解相差甚远。
案例12,方程组从形式上看非常简单,但实际求解计算,Antigone无法给出结果,其余四款求解器所得结果也均非正解,难道该方程组本身同样无解?
案例13,1stOpt仅能以大约10%的概率得到正解(有两组解,另一组x=[0.149 818 6,-0.329 753 6,-4 626.947 171 4]),其余求解器均无法获得正解,虽然Couenne的目标函数值趋近于0。如何提高正解获得率?
案例14源自于美国Matlab官方论坛一个问题,该论坛里的解答是该方程组无实数解,从Baron、Antigone、Couenne和Lingo所得结果看的确是无精确解,但1stOpt的结果显示解是存在的。
2.3 求解器评估
基于前述计算结果,从效果(目标函数值)与效率(计算时间)两方面可对五种求解器的总体优劣进行综合量化评估,具体是每个案例如果有解,则目标函数值和计算时间按从小到大,对应评分按5到1赋分;如果无解则得分均按0计。五种求解器的赋分表及最终得分见表3。综合得分越高表明该求解器综合能力越强。
一共14道测试题,满分最高分是140分,由上面赋分表可看出,综合得分最高的是1stOpt,其后依次为Antigone、Baron、Couenne和Lingo。五种求解器求解效果、求解效率及综合求解能力示意图分别见图4、图5及图6。

表3 求解器综合赋分表
2.4 方程简化与除法陷阱问题



(17)
A=BC
(18)
(19)
60x=2 664(x-0.85)
(20)
(21)
(22)
通过上述案例可以看出,导致理论上正确但实际错误的“罪魁祸首”就是“除法”,对比式(17)、式(19)和式(21)以及等效转换后的式(18)、式(20)和式(22),前者均含有未知数在分母的除法,后者经过等效乘法转换后消去了除法项。
再看前面测试案例7、10、12和13。其中案例7、10和12的式(9)、式(12)和式(14),通过等式乘除法变换,去掉方程中含有待求参数的分母项,修改后等价方程分别如式(23)、式(24)和式(25)所示。
(23)
(24)
(25)

表4 案例7、10、12、13形式变换后测试结果
上述方程五种求解器计算结果如表4所示。案例7的方程进行形式变换成式(23)形式后,Antigone和1stOpt可分别以100%和50%的概率得到正解;Couenne所得具体参数值与正解近似,但目标函数值相差巨大;Baron和Lingo维持原状,相比方程形式变换前没有任何改进。该方程组的特点就是其中一个参数值x3的数值非常小,达到1E-25的量级,但又不能等于0。
案例10方程形式变换后,1stOpt能以几乎100%概率获得正解,Baron和Antigone的结果也可视为正解虽然精度稍差;Couenne和Lingo结果仍然不对。此方程组最大的特点就是,不论哪个求解器,计算出的参数x4均等于-1.47,而在变换前的方程组中有分母项x4+1.47,因此会导致被0除的逻辑错误,从而导致无法得到正确结果。
案例12方程形式变换后全部五种求解器均可快速得到正解(该方程组是多解)。
案例13原方程组中不存在除法项,但仔细观察可发现方程中有“冗余”项,比如方程组中第二个方程可以通过等式两边同除以x1x2,同样第三个方程等式两边同除x3,简化后方程如下:
(26)
上述方程组1stOpt和Antigone求得正解的成功率分别从去除“冗余”项前的20%和0%提升至100%,其余3个求解器仍然无法获得正解。
通过上述四个实际案例可看出,方程组中如果存在除法项且除法项分母含有待求解未知参数时,应尽可能通过等效乘法变换去掉除法项,从而避免除法可能引起的“陷阱”;此外如果公式中存在“冗余”项也尽量将其消除简化。通过这样的变换,方程组正解求解率可大幅提高。
2.5 确定性算法与随机算法
Baron、Antigone、Couenne和Lingo均采用基于分支定界的确定性优化算法(Deterministic Global Optimization Algorithms)。采用确定性优化算法的求解器的特点之一就是每次计算都能得到稳定相同的结果,同时号称在一般情况下均能保证输出结果为全局最优,但在本文实际应用测试中却远远达不到所称结果为全局最优的水准;1stOpt采用自行研发的全局通用优化算法(Universal Global Optimization-UGO),大部分情况都能得到比前述四个求解器更好的结果,虽然不清楚UGO算法的具体实现方法,但从实际计算看,该算法明显不同于确定性算法,而是含有“随机”因子,其具体表现为:虽然对大多数问题都能计算获得稳定最优结果,但对少部分非常复杂或多解的问题,每次计算结果有可能不同或得到不同的解。
3 结 语
论文中首次提出的14道非线性方程组测试题集,具有规模小但非线性程度高及求解难度大的特点,非常适合用于检验测试和评估全局优化算法及相关求解器的计算效果和效率。
科学数值计算软件传统上基本是欧美产品占绝对统治垄断地位,但本次测试对比研究结果表明,至少在非线性全局优化求解领域,五款优化求解器中,测试综合排名由高到低依次为1stOpt、Antigone、Baron、Couenne和Lingo。开源免费的Couenne并非最差,反而是非常人气的商业求解器Lingo排名最后,而整体综合表现最好的是国产的1stOpt,不论是效果还是效率,均综合排名第一。
对比研究的五款求解器,除1stOpt为唯一的国产外,其余四款均来自美国,而令人惊讶的是这四款软件中的三款又都与卡耐基梅隆大学有关,Baron的创始人是现任卡耐基梅隆大学的Sahinidis教授,Antigone求解器的两位主要创始人之一的普林斯顿大学Floudas教授其博士学位于1986年在卡耐基梅隆大学获得,开源的Couenne求解器起源于2006年IBM与卡耐基梅隆大学的一个合作项目。卡耐基梅隆大学的计算机学科常年排行美国第一,仅通过本次研究的求解器也可窥一斑。
Baron的开发者Sahinidis教授和Antigone的开发者Floudas教授,他们本身的专业都是化学工程而非计算机或应用数学类,Lingo所属公司的CEO专业是环境工程,1stOpt的主要开发者据了解是土木工程,优秀的数学类计算软件却都是由非计算机和非数学专业的“行业外”人士开发或掌控,这一“跨行业”现象非常值得思考。
除了算法和求解器外,非线性方程组全局优化求解过程中一定要注意尽量避免“除法陷阱”这一问题,同时方程形式能简化的一定要先简化,只有这样才能确保大概率获得最优正解。此外,鉴于非线性全局优化问题的多样性和复杂性,测试所得五款求解器的综合求解能力仅仅基于本文的案例题集,期待将来更多研究者基于更多案例问题的测试结果。
最后还有两点需要说明,一是本次研究仅探讨了低维无约束非线性方程组全局优化求解问题,更高维数且含有约束条件的情况有待下一步实施进行;二是五款求解器均使用缺省设置,对于基于GAMS平台的四款求解器,参数求解的起始初值均为0,有可能导致被0除的错误现象发生,应特别注意。

