一种考虑群体智慧的直觉模糊群决策方法

裴 凤, 何雨薇, 闫 安, 杨爱峰

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

因为客观世界的复杂性以及人们知识结构和认知能力的差异性,所以需要在群决策过程中对不同个体的意见进行协调,这就是考虑共识性的群决策问题[1]。共识模型是协助群体达成共识的有效方法,但是大多数共识模型普遍假设专家是独立的。在实际的群决策问题中,专家的决策行为通常受到他们之间的信任、情感等关系的影响。因此,构建基于社会网络关系的共识模型引起了许多学者[2-4]的关注。

现有共识模型虽然有效地提高了专家的共识度,但很少考虑提升群体智慧(collective intelligence,CI)水平。文献[5]将CI分开解释,群体是描述一群人不需要有相同的态度或观点,从而能够更好地解决给定的问题;智慧是指利用自己对知识的学习、理解,然后适应变化、解决困难的能力。麻省理工学院将这2个词语结合在一起,广义地描述了由个体组成的群体做决策很有智慧性。拥有较高的CI水平是一个群体探索更优方案的前提,在执行相同任务时会比其他群体表现得更好。文献[6]认为,当一个群体的共识度过高时,CI水平可能会降低。此时,可以利用不信任关系使群体达到较高的CI水平,由于不信任专家的偏好信息可以使群体产生讨论,从而探索更优的方案,而不是群体意见过早地收敛于一个次优方案[7]。

受此启发,本文构建一个共识模型,该模型在对共识度低于阈值且自信度低于阈值的专家偏好进行修正时,既考虑信任专家的偏好信息,也考虑不信任专家的偏好信息,基于自信度和他信度确定共识模型中的调整参数,以促使群体有效地达成共识;然后从理论上证明该模型的有效性;最后通过信任度确定专家权重以集结各专家偏好信息,并给出方案的优劣排序结果。

1 预备知识

1.1 分布式语言信任关系

因为人们的社会行为相互影响,所以对社会个体的行为进行预测,就需要对他们之间的关系进行研究,信任关系就是其中常见的一种关系。人们不仅可以用“信任”“不信任”来表达与他人的信任关系,更可以用“高”“中”“低”语言等级来描述这种关系的强弱。例如,设H={Hα│α=1,2,…,π}为一个明确的完全有序离散术语集[8],Hα表示一个语言变量,则有9个术语等级的集合H可以表示为:

H={H1=非常差；H2=很差；H3=差；

H4=较差；H5=一般；H6=较好；

H7=好；H8=很好；H9=非常好}。

文献[9]基于上述语言变量模型,定义了一种分布式语言信任函数。

定义1 设H为一个离散语言术语集,

T={(Hα,φα)│α=1,2,…,π}

(1)

表示分布式语言信任函数。

其中:Hα∈H；φα为Hα的评估权重,满足φ1+φ2+…+φπ=1且φα≥0。

基于分布式语言信任函数表示专家之间的信任关系见定义2。

定义2[9]设专家集合e={e1,e2,…,em},对于∀h,k=1,2,…,m,都有专家eh对专家ek的分布式语言信任函数Thk,则矩阵

为专家集e的分布式语言信任关系矩阵。若h=k,则Thk表示专家对自己的信任评价;否则为对他人的信任评价。

为了度量专家之间的信任程度,文献[10]提出用期望值来表示Thk大小的方法。

定义3 分布式语言信任函数Thk的期望值如下：

(2)

其中,uHα为Hα等级的效用值,且有uH1+uH2+…+uHπ=1。为了表达方便,令thk=E(Thk)为eh对ek的信任度,若thk的值越大,则专家eh对ek的信任度越高。thk组成的矩阵为模糊信任关系矩阵SL。

设定阈值ε,当thk>ε时,ek为eh的信任专家；否则为不信任专家。特别地,当h=k时,若thk>ε,则ek为自信的专家；否则为不自信的专家。

1.2 直觉模糊互补关系矩阵

在群决策过程中,需要专家对方案进行评估并发表自己的意见。

当问题比较复杂时,专家往往不易直接给出方案的优先序,但是比较容易用直觉模糊数的形式给出方案两两比较的结果,这种比较结果带有犹豫的部分,更符合现实情况。

定义4[11]关于一组有限方案集X={x1,x2,…,xn}的偏好矩阵R=(rij)n×n为一个直觉模糊互补关系矩阵。对∀i,j=1,2,…,n，都有rij=〈μ(xi,xj),γ(xi,xj)〉。为了表示简洁,令rij=(μij,γij),其中：隶属度μij为方案xi优于xj的程度；非隶属度γij为方案xi劣于xj的程度。μij、γij满足以下特征：

0≤μij+γij≤1,μij=γji,

μii=γii=0.5, ∀i,j=1,2,…,n

(3)

πij=1-μij-γij表示专家在2个方案相比较时的犹豫度。

1.3 共识度测度

为了获得专家的共识度,本文采用文献[12]提出的共识测度方法。

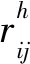
(4)

然后在专家个体层次上建立共识度,则专家eh与群体之间的共识度定义为:

(5)

Ch(0≤Ch≤1)的值越大,表示专家eh的共识度越高。

2 基于社会网络关系的共识模型

在群决策过程中,需要每位专家对于同一个方案的意见达成共识,这并非意味着他们的意见必须完全相同,而是说他们对相同方案偏好的差异应该在一定的范围内。一般设定阈值β∈[0.5,1],当所有专家的共识度都大于或等于β时,说明该群体达成共识,否则需要对共识度小于β的专家的偏好矩阵进行修正。

在对专家的偏好矩阵进行修正时,从提升CI水平的角度来看,不仅要考虑信任专家的意见,还要适当考虑不信任专家的意见。根据文献[6],当一个群体的社会关系密度较低时,CI水平和不信任关系成反比,即不信任专家的意见对于CI水平的提升是不利的;而当一个群体的社会关系密度为中等或较高时,CI水平和不信任关系成倒U关系,即适当采取不信任专家的意见可以使专家产生思考,群体将会探索更好的解决方案,CI水平将有所上升,而不是过早地向一个商定的次优解决方案趋同,形成无意识的抱团现象。

基于以上研究结果,本文将针对拥有不同社会关系密度的群体给予不同的修正方法。首先基于信任关系矩阵,给出社会关系密度的度量方法。

定义5 已知一个群体的信任关系矩阵SL,thk为专家eh对ek的信任度,此群体的社会关系密度ρ为:

(6)

给定阈值σ,若ρ<σ,则称该群体社会关系密度低；否则称社会关系密度中等或较高。根据文献[6]的结果,在此令σ=0.3。

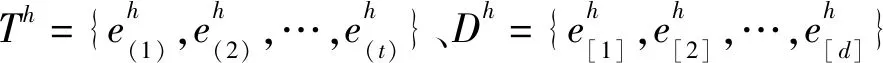
假设ex为共识度低于β且自信度低于ε的专家,则对该专家的偏好值调整为：

(7)

θ1=txx

(8)

(9)

(10)

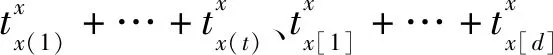
易证θ1+θ2+θ3=1。

根据以上分析,具体的共识调整方法如下。

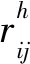
输出:Rh=Rlh。

(2) 计算社会关系密度ρ。

(5) 识别共识度最低的专家ex,若txx<ε,则执行下一步；否则在剩下的专家中继续识别共识度最低的专家,直至识别到Cy<β且tyy<ε的专家ey,然后执行下一步。

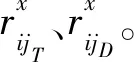
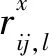
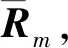
证明设ϑ为一个介于所有专家共识度最小值和第二小值之间的一个数,如果em的共识度低于阈值且其为共识度最低的专家,即有Cm<ϑ,那么对于其他专家eh(h=1,2,…,m-1)都有Ch>ϑ。存在em的信任专家集合为:

不信任专家集合为:

em的初始共识度为：

为了证明过程的简洁性,记

|μm-μG|+|γm-γG|=

因为Cm<ϑ,所以

Cm=1-|μm-μG|+|γm-γG|<ϑ

(11)

(11)式可表示为：

|μm-μG|+|γm-γG|>1-ϑ

(12)

则对于任意h∈{1,2,…,m-1},有

|μh-μG|+|γh-γG|<1-ϑ

(13)

下面证明：

|μm-μG|+|γm-γG|

(14)

当ρ≤0.3时,有

θ1(|μm-μG|+|γm-γG| )+

因为{(1),(2),…,(t) }⊆{1,2,…,m-1},所以根据(13)式,有

|γm-γG| )+(1-ϑ)(1-θ1)。

联系(12)式,有

θ1(|μm-μG|+|γm-γG|)+

(1-ϑ)(1-θ1)<|μm-μG|+|γm-γG|,

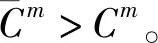
3 方案选择过程

如果当群体内所有专家的共识度都大于阈值,说明该群体达成共识,那么可以对各专家的偏好矩阵进行融合,然后对各方案进行排序,这样得到的最终解才更容易被专家接受。

首先,根据信任度确定专家重要性指标。根据文献[13],专家eh(h=1,2,…,m)的重要性指标为：

(15)

对重要性指标归一化：

(16)

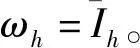
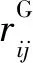
(17)

每个方案xi的得分函数fi如下：

(18)

fi值越大,说明方案xi越优。

4 应用实例

某学校有5位教师{x1,x2,x3,x4,x5}申请副教授职称,学校组建了一个专家评估小组,小组成员由4名专家{e1,e2,e3,e4}组成[14]。

为了简洁,设置三级语言量表H={H1=低；H2=一般；H3=高}。4名专家之间的分布式语言信任关系矩阵为：

4名专家给出的偏好矩阵分别为：

(1) 转化信任关系表示形式。设定3个等级的效用值分别为uH1=1/6、uH2=1/3、uH3=1/2。根据(2)式,将分布式语言信任关系矩阵转化为模糊信任关系矩阵。模糊信任关系矩阵为：

(2) 融合专家偏好矩阵。根据(15)式、(16)式可以得到,专家的权重分别为0.27、0.26、0.23、0.24。根据(17)式得到群体偏好矩阵为：

(3) 计算共识度。根据(4)式、(5)式,每位专家的共识度分别为:

C1=0.92,C2=0.91,

C3=0.86,C4=0.94。

(4) 调整偏好值。首先根据(6)式计算得到专家组的社会关系密度ρ=0.34。因为该评估小组属于关系亲密性中等的群体,所以在进行偏好值修正时要同时采取信任和不信任专家的偏好值。

然后给定共识度阈值β=0.90,信任关系阈值ε=0.33。

因为专家e3共识度小于β且自信度低于ε,所以需要对e3的偏好值进行修正。

获得e3信任和不信任专家集合分别为：

T3={e1,e4}、D3={e2}。

根据信任度,调整参数θ1、θ2、θ3的数值分别为0.27、0.54、0.19,那么修正后e3的偏好矩阵为：

(5) 方案排序。首先需要融合修正后的专家偏好矩阵。根据(17)式得到群体偏好矩阵为：

然后对教师进行排序。根据(18)式,5个教师的得分函数分别为:f1=1.55,f2=1.52,f3=0.33,f4=-1.60,f5=-1.80。因此方案的排序为x1≻x2≻x3≻x4≻x5,这与文献[14]中的结果一致。

5 结 论

本文是在以往共识模型的基础上,探讨了不信任关系在共识达成过程中的作用,并确定调整参数的值。首先在共识模型构建时引入群体智慧的概念,说明以往没有考虑不信任关系的共识模型的劣势,即群体意见会过早地向一个次优解决方案趋同;其次定义基于信任度的社会关系密度度量方法,分别对处于不同社会关系密度的群体提出不同的偏好值修正方法,以构建共识模型;然后根据自信度与他信度确定共识模型中的调整参数;最后基于信任度求出各个专家的权重,以融合各个专家偏好矩阵得到群体的偏好矩阵,并对方案进行排序。

虽然本文中的共识模型可以使专家达成共识,但是本文在讨论时选取的专家数量较少,而专家数大于20 的大规模群决策是一个值得进一步探讨的问题,今后将对大规模群决策的共识模型进行研究。