高速钢工作辊温度分布和考虑平均应力的热疲劳寿命研究

宋守许, 张志旭, 蔚 辰

(合肥工业大学 机械工程学院,安徽 合肥 230009)

我国是全球最大的冶金轧辊生产和消耗国,年淘汰各类轧辊约1.56×106t,造成了严重的资源浪费。而热轧轧辊失效的一个重要原因是表面承受剧烈的热载荷,从而导致热疲劳失效,因此,对于热轧轧辊热疲劳行为的研究尤为重要。文献[1]首次测量了轧辊热轧过程中辊体温度分布情况,证明了在热轧过程中工作辊表面温度可高达500 ℃;文献[2]设计了复杂而巧妙的实验,测出工作辊不同深度下热轧过程温度分布情况;但由于工作辊工作时处于旋转状态,表面和内部各相关参数难以设计实验测量,可靠的工业实测数据较少。相较之下,传热分析和热应力的理论基础已经较为完善,因此对于工作辊的热行为分析多基于仿真的方法。

热轧过程中工作辊需承受严重的循环热载荷,其引起的热疲劳是轧辊失效的主要原因之一。为研究工作辊热轧过程中的热行为,国内外学者在建立轧辊有限元模型方面进行了有益的探索[3-4]。文献[5]建立了工作辊温度场的差分模型,研究了轧辊表面温度与热膨胀量;文献[6]基于生死单元法研究了典型工况下辊面温度时间历程;文献[7-8]通过将传热边界条件等效为对流传热,模拟了轧辊热轧条件,得出了不同情况下工作辊近表面温度分布和热应力曲线;文献[3]根据实际轧制情况施加边界条件,研究了工作辊径向和轴向温度变化情况以及轧制速度和轧制节奏对工作辊温度场的影响。对于工作辊热疲劳寿命的计算也有了一些研究。文献[9-10]在考虑残余应力的影响下对工作辊热轧过程的温度分布以及热应力进行了细致的研究,并根据Manson-Coffin公式给出了工作辊热疲劳寿命;文献[11]比较了Manson-Coffin公式以及考虑应力多轴的表面热疲劳寿命,得出在考虑应力多轴的情况下计算所得的疲劳寿命远低于单轴应力下疲劳寿命估算值的结论。

国内外近年来有部分模拟真实工况的轧辊热行为分析的研究,并且通过基于应变的疲劳寿命公式给出了对热轧过程中工作辊的热疲劳寿命预测,但在将Manson-Coffin公式应用到工作辊热疲劳寿命的计算时没有考虑平均应力的影响,而这在本文中被证明是不能忽略的。本文模拟真实工况,采用弹塑性有限元法对热轧过程进行热学分析,并以Manson-Coffin公式为基础,在考虑平均应力的影响下给出工作辊热疲劳寿命的计算。

1 有限元模型建立

1.1 传热方程

热轧过程中高速钢工作辊的温度分布是一个瞬态热问题,在不考虑边缘效应的情况下,高速钢工作辊的传热可以看作无限长圆柱体的传热问题,从而忽略温度沿轴向的传导，由此可将工作辊的热传导看作一个二维无热源的传热问题。在二维极坐标下无热源非稳态导热微分方程为:

(1)

其中:T为工作辊的温度分布;r、θ分别为半径和角度坐标;λ为热导率;t为时间;ρ、c分别为材料的密度和比热容。

热扩散率为：

代入(1)式,计算可得:

(2)

工作辊转速恒定,则有：

代入(2)式并计算得到:

(3)

其中:R为工作辊圆周半径;V为工作辊最外层线速度。

1.2 有限元模型描述

在四辊七机架轧机的热轧过程中,前4个机架转速慢、带钢温度高,工作辊表面温度变化剧烈,热应力是其失效的主要原因。因此,本文以F3机架工作辊的精轧过程为研究对象,研究F3机架工作辊的温度分布、热应力应变以及由此引发的热疲劳失效。本文建立了一个二维轧辊模型,采用Abaqus/Standard的完全耦合热应力分析方法。模型为一个旋转的工作辊,对其施加传热边界条件,以模拟其热轧过程中的热行为。工作辊表面熔覆层材料为CW6Mo5Cr4V3高速钢,芯材为球墨铸铁，其材料属性[11]见表1所列,轧制参数见表2所列。

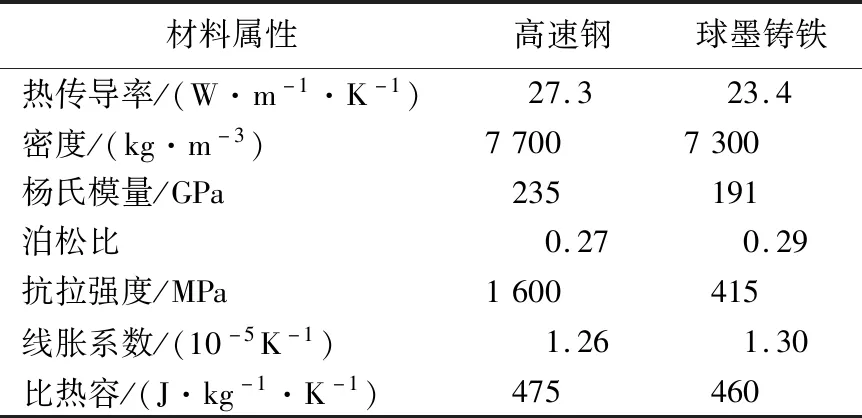
表1 高速钢和球墨铸铁材料属性

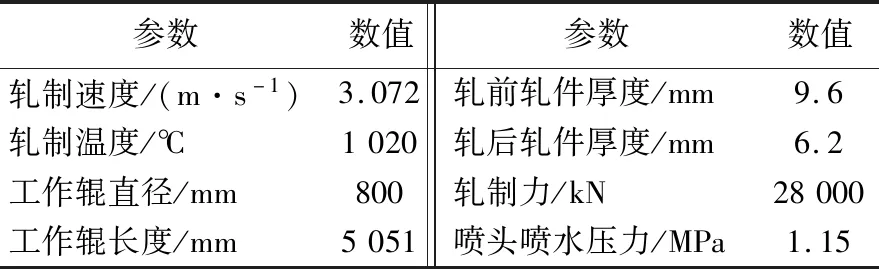
表2 模型轧制技术参数

轧辊轧制示意图如图1所示,工作辊和支撑辊为上下对称的一对,图1只画出上半部分。

轧制过程为:带钢有一个初速度,工作辊转速为ω,带钢与工作辊接触后靠与工作辊之间的摩擦力带动向前,完成轧制。热轧过程中工作辊可分为如下区域:AB区域为咬合区,高温带钢对工作辊传热;BC、EF、FG、IA区域为空气自然对流散热区;DE、GH区域为喷水强制对流散热区,喷水冷却可保证工作辊在长时间的热轧过程中对工作辊近表面迅速降温;DC、HI为积水区,挡板可以防止积水落在高温的带钢上。

大量研究[7-11]表明,前4个机架工作辊的损伤主要由热应力引起。本文主要研究工作辊热轧过程中的抗热性能,因此所建模型不考虑轧制过程中的机械应力,只考虑热应力,以研究工作辊的热疲劳现象。

工作辊有限元模型网格划分及局部放大图如图2所示。

图2中网格的划分能确保工作辊近表面温度和热应力梯度较大的区域网格足够细致且总网格数尽可能少,从而在保证计算精度的前提下减少计算量。网格单元类型选择为CPE4RT。

1.3 热边界条件计算

对工作辊施加等效热边界条件以模拟轧制过程中的热行为,通常将热边界条件等效为对流换热,并计算相应部分传热系数h。

工作辊旋转过程中一周的传热系数示意图如图3所示。

工作辊不同区域表面传热系数不同,咬合区、喷水区、积水区和空气自然冷却区传热系数计算分别如下:

在咬合区(AB),相关学者考虑了表面粗造度、轧制力和带钢流动应力的影响,建立了相关经验公式[12],具体如下:

(4)

(5)

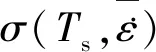
带钢流动应力计算公式为:

(6)

(7)

其中:T=(t+273)/1 000,t为变形温度;um为轧制平均变形速度;lc为轧辊与轧件接触弧的水平投影长度;H、h为轧制前、后轧件厚度;σ0、a1～a6为回归系数。计算得出带钢流动应力为162.7 MPa。

在空气自然对流冷却区(BC、EF、FG、IA),工作辊与空气自然对流传热系数hair的计算公式[11]如下:

hair=1.465(Ts-Ta)1/3

(8)

其中,Ta为空气温度。BC区工作辊表面温度较高,其对流传热系数比EF区和FG区高。

在积水区(CD、HI),冷却水传热系数hwiper计算公式[8-10]如下:

(9)

(10)

(11)

其中:Re为雷诺数;Prcw为积水的Prandtl常数;λcw为积水热导率;lc为挡水板与工作辊接触弧长;υcw为积水的运动黏度,υcw=μcw/ρcw,μcw为积水的动力黏度;ρcw、ccw为冷却水的密度和比热容。

在喷水区(DE、GH),由于工作辊表面温度不同,DE区工作辊表面温度超过100 ℃,GH区表面温度低于100 ℃,其冷却水传热系数hcw计算公式[8-10]分别为:

(12)

(13)

其中:Tr为工作辊表面温度;Q=vsp/Asp,为单位面积喷水量,vsp为喷水速度,Asp为喷射面积;Psp为喷头水压;Twa为冷却水温度。

计算得出各区域传热系数,见表3所列。

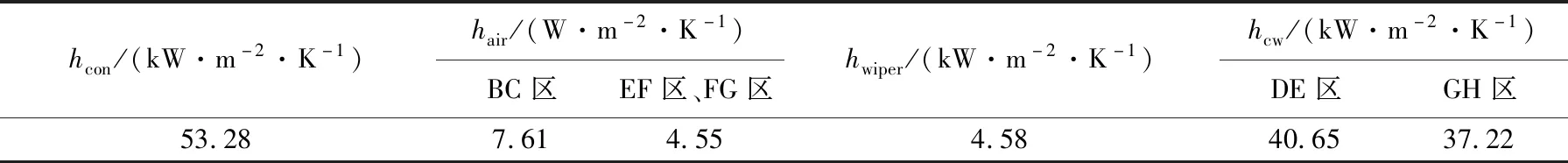
表3 工作辊表面各区域传热系数

2 仿真结果分析

2.1 热轧过程中工作辊温度分布

工作辊热轧过程中温度分布云图如图4a所示,温度分布局部放大图如图4b所示。从图4可以看出,工作辊在咬合区附近表面温度梯度较大,而后经过水冷迅速降温。

因为持续地喷水冷却,热量很难往内部传递,所以温度集中在表面薄层,在工作辊内部几乎为常温。

工作辊近表面温度分布如图5所示,工作辊表面温度变化剧烈。初轧时,AB段在咬合区内表面温度迅速上升至438.7 ℃,BC段由于往内部传热以及空气自然对流散热,温度降至100.2 ℃,经过积水区CD段和喷水区DE段降至常温,EF和FG段因为辊内温度高于表面温度,工作辊内部往表面传热,表面温度略有上升,直到经过喷水区GH与积水区HI后再次降温。而后IA段表面温度变化不大,直至下一轧制循环。经过几个轧制周期后表面最高温度稳定在463.8 ℃。

图5标出了近表面沿径向温度的变化,r/R指曲线所对应的深度与工作辊直径的比值。在咬合区工作辊近表面沿径向温度梯度很大,经过15个轧制周期后,距表面0.8 mm处温度稳定在139.5 ℃,距表面2.1 mm处温度为91.2 ℃,距表面4.0 mm处温度为73.3 ℃,且随着轧制时间的增加,温度还会缓慢上升至稳态。

由此可见,工作辊径向传热较慢,工作辊咬合区受热时间短,温度迅速上升,过了咬合区表面温度又迅速下降,而工作辊的热导率较低,是典型的表面温度变化剧烈而内部传热热阻大,需要很长时间温度才能传至芯部达到稳态。在冷却阶段,由于喷头的冷却作用,工作辊表面温度迅速降低至常温,且工作辊近表面温度高于表面温度,内部往表面传热,表面在冷却水冷却下降温,逐渐使整个辊温度趋于常温。工作辊表面温度的迅速上升和下降必然会导致应力的急剧变化,从而极大地影响工作辊使用寿命。

工作辊在咬合区AB段吸收热量为:

Φt=hconAΔTt,

其中:Φ为热流量;A为受热面积;ΔT为带钢与工作辊表面温差;t为时间。因此在忽略传热的情况下工作辊表面温度与受热时间成正相关,而受热时间由热轧速度决定。

F1～F4机架工作辊工况差异最大点在于热轧速度和下压量不同,其中热轧速度会导致表面最高温度不同。因此需要探讨热轧速度对工作辊温度分布的影响。不同转速下工作辊表面温度变化情况如图6所示。

由图6可知,随着转速的提高,工作辊表面温度明显下降。当转速为3.6 rad/s时,工作辊表面温度最高达到590.7 ℃;当转速为12.4 rad/s时,工作辊表面最高温度降到了368.1 ℃。结果表明,在一定范围内适当提高工作辊转速有利于降低工作辊表面最高温度,从而减少热应力,提高其热疲劳寿命。

2.2 热应力分析

物体均匀受热自由膨胀时会产生热应变,但膨胀不受约束时,物体内部不会产生热应力。而工作辊在热轧过程中受热是非均匀且变化的,工作辊咬合区受热膨胀,由于径向没有边界条件的限制,可以自由膨胀,径向应力σr几乎为0。而周向的膨胀会受到周围单元的挤压,膨胀受阻,从而产生较大的周向压应力σθ,如图7所示。

工作辊热轧一周在4个选定的深度热应力变化情况如图8所示，其表面周向应力在经过咬合区AB段后达到最大,为-945.3 MPa,负号表示压应力。

从图8可以看出,随着表面温度的迅速下降以及表面与内部温差的减小,周向压应力在C处减小至-207.7 MPa,经过积水区CD段和喷水区DE段,应力进一步降低至-30.1 MPa,E到I段由于温度变化较小,热应力变化不大,直至下一轧制周期。经过15个轧制周期后表面最大周向压应力稳定在-980.8 MPa。

从图8还可以看出,工作辊表面大的温度梯度导致了大的热应力梯度,距表面0.8 mm处应力最高稳定在-314.0 MPa,距表面2.1 mm处应力为-190.9 MPa,距表面4.0 mm处应力为-134.9 MPa。

由图8可知,工作辊热轧过程中表面周向应力为压应力,对1个周期内表面周向应力积分并除以积分区间长度可算出表面周向应力的平均应力,为-95.7 MPa。

3 热疲劳寿命预测

工作辊在热轧过程中承受严重的循环热应力,塑性应变的累积超出了高速钢材料的弹性范围,其寿命由应变而非应力决定。

由Manson和Coffin提出的综合考虑弹性和塑性形变对疲劳寿命累积影响的公式[13]被广泛应用,即

(14)

其中:Δε为总应变范围;Δεe为弹性应变幅值;Δεp为塑性应变幅值;σf′为疲劳强度系数;εf′为疲劳延性系数;E为弹性模量;Nf为疲劳寿命;b为疲劳强度因子;c为疲劳延伸指数。

因为σf′、εf′需要通过单轴疲劳试验获得,耗时长、成本高,所以文献[14-15]进一步提出了通用斜坡方程,并通过测试29种金属材料得出了适用所有金属材料的b值和c值(b=-0.12,c=-0.6)。

通用斜坡方程如下:

(15)

其中:Δεeq为等效应变;ν为泊松比;σUTS为抗拉强度;D为材料延展性,由-ln(1-AR)计算确定,AR为试件断裂减缩面积,取16%。

Δεeq计算如下:

(16)

其中:ε1、ε2、ε3为第一、第二、第三主应变(主应变值唯一,与坐标系选择无关);Δ(εi-εj)为在一定参考时间内的主应变差值。

由(15)式作出双对数坐标下工作辊等效应变与疲劳寿命关系图,如图9所示。

由图9可知:当等效应变较小时,工作辊疲劳的主要贡献为弹性累积损伤;而当等效应变较大时,主要贡献为塑性累积损伤。

当主要贡献为弹性累积损伤时,工作辊疲劳寿命较长,且随等效应变的减小而指数增大,并趋近于弹性线;当主要贡献为塑性累积损伤时,工作辊疲劳寿命较短,且随等效应变的增大而指数减小,并趋近于塑性线。

热轧3个周期内主应变差值Δ(εi-εj)和等效应变Δεeq随时间的变化如图10所示。其中:第一、第二、第三主应变由有限元仿真结果导出;等效应变Δεeq由(16)式计算得出。

从图10可以看出，在热轧15个周期后,工作辊等效应变稳定在0.004 47。

文献[3]将原始的Manson-Coffin公式(即通用斜坡公式)以及考虑应力多轴性的通用斜坡公式应用到工作辊热轧过程热疲劳寿命的计算中。然而,原始的Manson-Coffin公式是由单轴疲劳试验得出的,试验中的试件承受的是循环对称载荷,其应力随时间变化的示意图如图11所示,可以看出平均应力为0。

显然，生产生活中很少有循环对称载荷的情况。工作辊表面热应力情况示意图如图12所示，其所承受的热应力平均值不为0。当平均应力不为0时，对于Manson-Coffin公式的应用必须考虑平均应力的修正。

文献[16]提出了一种处理平均应力对寿命影响的方法,采用Morrow准则,修正公式如下:

(17)

Veff=kVσ

(18)

Vσ=σm/σa

(19)

k=exp[-70(Δεin/Δεel)2]

(20)

其中:Nfm为平均应力修正后工作辊疲劳寿命;Nf0为(15)式计算得到的平均应力为0时的疲劳寿命;σa为应力幅值;σm为平均应力;Δεin为塑性应变;Δεel为弹性应变;k为选取的平滑过渡函数,其值随Δεin/Δεel变化。

平滑过渡函数k随Δεin/Δεel变化的曲线如图13所示。

由上文热应力分析可知,表面周向应力的平均应力为-95.7 MPa,根据(15)式、(17)式可计算得出平均应力修正前、后的工作辊热疲劳寿命,计算结果见表4所列。

表4 工作辊热疲劳寿命计算对比

从表4可以看出:原始的Manson-Coffin公式忽略了平均应力对工作辊热疲劳寿命的影响,得出的疲劳寿命估计值较为乐观;考虑平均应力影响后热疲劳寿命变为464 727转,比不考虑平均应力的计算结果提升19.9%。由此可见,当平均应力为压应力时,考虑平均应力的影响会提高热疲劳寿命的计算值。在将Manson-Coffin公式应用到工作辊热疲劳寿命的计算中时必须考虑平均应力的修正。

4 结 论

本文提出了对于高速钢工作辊热轧过程中热应力应变分析和热疲劳寿命评估的方法,该方法基于工作辊在热轧旋转热负载下的二维有限元模型,得出如下结论:

(1) 进行了瞬态热仿真,热分析结果表明,工作辊表面一周温度变化剧烈,最大处稳定后可达463.8 ℃;且在工作辊表层存在较大的热梯度,温度沿径向传播较慢。转速的提高有利于工作辊表面最高温度的降低,从而延长工作辊热疲劳寿命。

(2) 热应力分析结果表明,工作辊表面径向应力几乎为0,周向压应力最大可达-980.8 MPa,近表面周向压应力梯度较大,是热疲劳发生的主要区域。分析得到工作辊表面周向压应力的平均值为-95.7 MPa。

(3) 考虑平均应力对热疲劳寿命计算的影响,将修正前、后得到的工作辊热疲劳寿命进行对比。结果表明,平均应力对工作辊热疲劳寿命的计算值影响较大,平均应力为压应力时,考虑平均应力会提高热疲劳寿命的计算值。研究结果使Manson-Coffin公式在工作辊热轧过程中的热疲劳寿命计算应用更加符合实际情况。