具有扰动的脉冲系统的渐近稳定性
倪郁东, 韩姣杰
(合肥工业大学 数学学院,安徽 合肥 230601)
脉冲能引起系统状态的变化,进而改变所期望的稳定性,因此对脉冲系统的渐近稳定性分析具有一定的现实意义[1-3]。脉冲系统可表述为:
(1)
其中:k=1,2,…;x∈Rn为状态变量;脉冲时刻序列{τk}满足0<τ1<…<…,k=1,2,…,当k→∞时,τk→∞;系统描述函数f(t,x(t)):R+×Rn→Rn和脉冲量函数uk(x):Rn→Rn均为连续性函数。
在实际的系统中,由于系统结构本身的原因,如机械设备的限制、机器老化等,都会使脉冲系统的稳定性受到相应干扰,当把这些扰动因素添加到系统中并对其进行分析时,系统(1)便成了具有扰动的脉冲系统(2)。当脉冲系统(1)受到R(t,x(t)):R+×Rn→Rn扰动后的系统形式为:
(2)
其中,k=1,2,…。
近年来,研究者关于扰动后的脉冲系统进行了大量的研究和应用[4-6]。文献[7]将扰动项加入陈氏混沌系统中,利用脉冲控制的方法,使受不确定扰动的陈氏混沌系统渐近稳定到平衡点,得到受扰动的陈氏混沌系统鲁棒稳定的充分条件;文献[8]通过构造Lyapunov函数将脉冲系统的解与具有扰动的脉冲系统的解连接起来,再根据Lyapunov直接方法和比较原理,分析了扰动后系统的最终Lipschitz稳定性,但是当系统不易求解时,再利用解对系统进行分析相对困难;文献[9]在原有Lyapunov函数V(t,x)的基础上构造了一个新的、适用于受扰动后脉冲系统的Lyapunov函数V(t,x)=V1(t,x)+Ψ(t,x),证明了有扰动的非线性脉冲系统的一致渐近稳定的充分条件,其侧重点是构造函数Ψ(t,x);文献[10]通过构造类似Lyapunov函数的分段连续辅助函数,建立了系统保持一致最终稳定的充分条件。
在分析脉冲系统的渐近稳定性时,研究者常采用比较系统法[11-15],根据脉冲系统的比较原理构造满足条件的比较系统,通过分析比较系统的稳定性得到脉冲系统渐近稳定的充分条件。该方法的主要思想是以Lyapunov函数为媒介,将较复杂的脉冲系统研究转换为一个相对简单的标量脉冲系统(即比较系统)研究,从而降低分析问题的难度,因此在研究脉冲问题时多采用此方法。
系统(1)受到R(t,x(t))扰动后,若仍用判断系统(1)渐近稳定的比较原理和比较系统分析扰动后系统(2)的稳定性,则需重新建立比较系统和比较原理,否则会忽略扰动项的特性。本文充分考虑范数有界扰动R(t,x(t))的作用,根据比较系统法,建立能够判断系统(2)渐近稳定的比较原理和比较系统,得到系统(2)渐近稳定的充分条件。具体过程如下:对系统(1)的比较系统进行调整,利用扰动R(t,x(t))和系统(1)Lyapunov函数V(t,x)控制量,构造系统(2)的比较系统,同时建立有关系统(2)和比较系统的引理,再调整系统(1)比较原理的条件,结合引理建立能够判断系统(2)稳定的比较原理。系统(2)的Lyapunov函数是通过对系统(1)的V(t,x)进行变易,选取K(t)V(t,x)对扰动后的系统进行分析,构造满足比较原理条件的比较系统,通过分析比较系统的渐近稳定性得到扰动后脉冲系统渐近稳定的充分条件,Bx函数的适当选取有利于满足扰动后脉冲系统渐近稳定的条件。本文还考虑:系统描述函数为非线性函数,脉冲量分别为线性函数Bx和可变线性函数Bkx的系统,分析得到2种系统渐近稳定的充分条件,最后通过数值示例验证方法的有效性。
1 理论基础
定义1 设ε>0,t0∈R+,称函数x(t):[t0,t0+ε)→Rn为系统(2)的一个解,若以下条件成立:
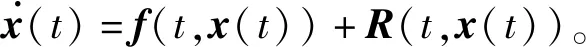
(3) 当t∈[t0,t0+ε)且t≠τk时,x(t)左连续,即x(t-)=x(t)且x(t+)=x(t)+uk(x(t))。
定义2 设V:R+×Rn→R+,称V是属于V0类的,如果V满足:
(1) 函数V在(τk-1,τk]×Rn上是连续的,且对每一个x∈Rn,k=1,2,…,有
(2) 函数V关于x满足局部Lipschitz条件,即对任意x1,x2∈Rn,存在l>0,有
|V(t,x1)-V(t,x2)|≤l‖x1-x2‖
成立,且对所有的t∈R+,有V(t,0)=0。
定义3 对任意(t,x)∈(τk-1,τk]×Rn,k=1,2,…,定义
hf(t,x(t))-V(t,x)],
h(f(t,x(t)+R(t,x)))-V(t,x)]。
定义4 对任意α(s)∈C[R+,R+],若α(0)=0且α(s)为严格单调增函数,则称α(s)为K类函数。
定义5 对任意ε>0,存在δ=δ(ε,t0)>0,当‖x0‖<δ时,对于系统(2)的解x(t,t0,x0),均有‖x(t,t0,x0)‖<ε,t>t0,则称系统(2)的平凡解是稳定的。
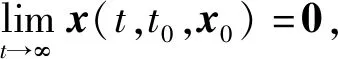
定义7 若系统(2)的平凡解既是稳定的也是吸引的,则称其是渐近稳定的。
定义8 设V∈V0,假设
(3)
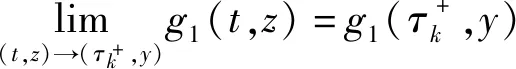
(4)
为系统(1)的比较系统
引理1[13]设V:R+×Rn→R+且V∈V0,假设
引理2[15]设V:R+×Rn→R+且V∈V0,K:R+→(0,+∞),对k=1,2,…,有
K(t)V(t,x(t,t0,x0))≤r(t,t0,w0)。
其中:r(t,t0,w0)为系统(4)在区间[t0,∞)上的最大解;g1(t,V(t,x))满足定义8的条件;ψk:R+→R+为非减函数。
引理3[15]假设如下:
(1)V:R+×Rn→R+且V∈V0,
g1(t,K(t)V(t,x)),t≠τk,
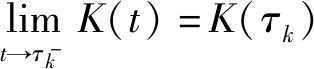
(2)K(t+)V(t+,x+uk(x))≤ψk(K(t+)×
V(t+,x)),t=τk,k=1,2,…。
(3) 存在函数α(·)∈K,满足α(‖x‖)≤
V(t,x)且V(t,0)=0。
则比较系统(4)的平凡解的稳定性蕴含着系统(1)的平凡解的稳定性。
引理4[16]若P∈Rn×n为正定矩阵,Q∈Rn×n为对称矩阵,则对任意向量x∈Rn,有
xTQx≤λmax(P-1Q)xTPx,
其中,λmax(P-1Q)为矩阵P-1Q的最大特征值。
引理5[17]对于在‖x‖<ρ上给定的任意正定连续函数V(t,x),必存在2个函数φ1、φ2∈K,使得:φ1(‖x‖)≤V(t,x)≤φ2(‖x‖)。
针对扰动后的系统(2),在构造它的比较系统时,需要考虑扰动项R(t,x(t))的存在,引理6利用扰动R(t,x(t))的控制量,以Lyapunov函数V(t,x)为媒介,对定义8中的条件进行调整,构造系统(2)的比较系统。
引理6 设V∈V0,α(‖x‖)≤V(t,x),‖x‖≤α-1(V(t,x)),设
(5)
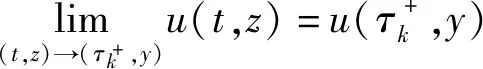
(6)
为系统(1)受扰动后系统(2)的比较系统,其中α-1(w)为α(w)的反函数。
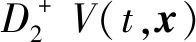
x+h(f(t,x)+R(t,x)))-V(t,x)]=
V(t+h,x+hf(t,x))+V(t+h,
x+hf(t,x))-V(t,x)]=
h(f(t,x)+R(t,x)))-V(t+h,x+hf(t,x))]。
由于V(t,x)在t∈(τk,τk+1]上关于x满足局部Lipschitz条件,由(5)式和u(t,w)关于w为非减函数可知,当t≠τk时,有
lu(t,α-1(V(t,x)))≤g1(t,V(t,x))+
lu(t,α-1(V(t,x)))=g(t,V(t,x))。
当t=τk时,有V(t,x+uk(x))≤ψk(V(t,x))。
根据条件可得其比较系统为:
考虑系统(2)的比较系统(6),对引理1中的条件进行调整,得到适用于比较系统(6)的下列引理。
引理7 考虑系统(6),假设
其中:r(t,t0,w0)为系统(6)在区间[t0,∞)上的最大解;g1满足定义8中的条件且满足系统(1)稳定时的比较条件;u满足引理6中的条件;ψk:R+→R+为非减函数。

定义
因此,对t≥t0,有V(t,x)≤r(t,t0,w0),其中r(t,t0,w0)为系统(6)在[t0,∞)上的最大解。
考虑扰动R(t,x(t))的特性,结合引理7对引理2的条件进行调整,得到适用于系统(6)的下列引理,其中系统(2)的Lyapunov函数是对系统(1)的Lyapunov函数V(t,x)进行变易,选取K(t)V(t,x)对系统(2)进行分析,一方面增加了其在系统中的实用性,另一方面K(t)函数的适当选取有利于满足扰动后脉冲系统渐近稳定的条件。
引理8 设V:R+×Rn→R+,且V∈V0,K:R+→(0,+∞),对k=1,2,…,有
其中:r(t,t0,w0)为系统(6)在区间[t0,∞)上的最大解;g1满足定义8中的条件且满足系统(1)稳定时的比较条件;u满足引理6中的条件;ψk:R+→R+为非减函数。
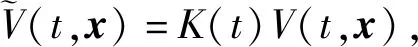
当t≠τk时,有
h(f(t,x)+R(t,x)))-K(t)V(t,x)]=
h(f(t,x)+R(t,x)))-K(t)V(t+h,x+
h(f(t,x)+R(t,x)))+K(t)V(t+h,x+
h(f(t,x)+R(t,x)))-K(t)V(t,x)]=
x+h(f(t,x)+R(t,x)))+
R(t,x))-V(t,x)]=V(t,x)D+K(t)+
由此可得:
即
对引理3的条件进行调整,得到能判断系统(2)渐近稳定的比较原理(即引理9)。
引理9 假设如下:
(1)f(t,0)=0,R(t,0)=0,g1(t,0)=0,u(t,0)=0,uk(0)=0。
(2)V:R+×Rn→R+且V∈V0,K(t)≥m>0,
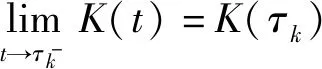
(3) 存在函数α(·)∈K,满足α(‖x‖)≤V(t,x)且V(t,0)=0,则比较系统(6)的平凡解的稳定性蕴含着系统(2)的平凡解的稳定性。
证明借鉴文献[15]中定理1的证明方法。由条件(1)可知,系统(2)和系统(6)的平凡解是存在的。假设系统(6)的平凡解是稳定的,r(t,t0,w0)为系统(6)在t≥t0上的最大解,则对任意ε>0,存在δ0=δ0(t0,ε)>0,当0 设δ=min{δ0,δ1},由引理8的结论、引理9的条件可知:当‖x0‖<δ时,有 mα(‖x‖)≤K(t)V(t,x(t,t0,x))≤ r(t,t0,w0) 即当‖x0‖<δ时,有‖x‖<ε,t≥0。 因此系统(2)的平凡解是稳定的。 现证明系统(2)的平凡解是吸引的。 w(t,t0,w0) 由引理8的结论、引理9的条件可得:当‖x0‖<δ时,有 mα(‖x‖)≤K(t)V(t,x(t,t0,x))≤ r(t,t0,w0) 其中,t≥t0+T。这说明系统(2)的平凡解是吸引的。因此系统(2)的平凡解是渐近稳定的。 采用比较系统法的思想,将较复杂的脉冲系统研究转化为一个相对简单的标量系统(比较系统)的研究,通过分析比较系统的稳定性得到系统(2)的渐近稳定性。下列引理考虑一种形式相对简单的系统,并证明其是渐近稳定的。 引理10 考虑以下形式的脉冲系统: (7) 若满足条件: (2) 存在γ>1,d2k+2d2k+1≠0,k=1,2,…, λ(τ2k+3)+λ(τ2k+2)+ 则系统(7)的平凡解是渐近稳定的。 证明对系统(7)的分析。当t∈(t0,τ1]时, 当t∈(τ1,τ2]时, 当t∈(τ2,τ3]时, 当t∈(τ2k-1,τ2k]时, 当t∈(τ2k,τ2k+1]时, 考虑如下形式的具有扰动的脉冲系统: (8) 其中,x∈Rn为状态变量;f(t,x):R+×Rn→Rn为非线性连续函数;R(t,x):R+×Rn→Rn为系统的非线性扰动项;B∈Rn×n为常数矩阵。 定理1 设P∈Rn×n为正定矩阵,λ1、λ2分别为矩阵P的最小和最大特征值,λ3为矩阵BTB的最大特征值。若扰动脉冲系统(8)满足以下条件: (2) 存在可微且不增的函数K(t),t≠τk,k=1,2,…,满足e-Mk>D2,其中 则系统(8)在平凡解处是渐近稳定的。 证明构造Lyapunov函数V(t,x)=xTPx,当t≠τk时, K(t)D+V(t,x)+V(t,x)D+K(t)= K(t)(f(t,x)+R(t,x))TPx+ K(t)xTP(f(t,x)+R(t,x))+ H(t)K(t)xTPx。 当t=τk时, xTBTPx+xTBTPBx≤ DK(τk)xTPx。 构造系统(8)的比较系统: Mk≤-ln[γλ3(τ2k+2)λ3(τ2k+1)]。 由条件(3)可知,λ1‖x‖≤V(t,x)=xTPx,根据引理9、引理10可知系统(8)是渐近稳定的。 定理1中,脉冲量为线性的且与控制节点数k(k=1,2,…)无关;但是在实际的系统中,有时为了达到某种目的,脉冲量与控制节点数是有关的,它会随着控制过程的进行而不断改变,此时有以下形式具有扰动的脉冲系统: (9) 其中:k=1,2,…;x∈Rn为状态变量;f(t,x(t)):R+×Rn→Rn为非线性连续函数;R(t,x(t)):R+×Rn→Rn为系统的非线性扰动项;Bk∈Rn×n为常数矩阵。 定理2 设P∈Rn×n为正定矩阵,λ1、λ2分别为矩阵P的最小和最大特征值,λ3(k)>0满足xT(I+Bk)TP(I+Bk)x≤λ3(k)xTPx,若系统(9)满足以下条件: (1) 与定理1的条件(1)相同。 (2) 存在可微且不增的函数K(t),t≠τk,k=1,2,…,满足e-Mk>λ3(τ2k+2)λ3(τ2k+1)。 证明构造Lyapunov函数为V(t,x)=xTPx,当t≠τk时,结果与定理1中当t≠τk时相同。 当t=τk时, 构造系统(9)的比较系统为: Mk≤-ln[γλ3(τ2k+2)λ3(τ2k+1)]。 由条件(3)可知,λ1‖x‖≤V(t,x)=xTPx,根据引理9、引理10可知系统(9)是渐近稳定的。 本文研究在范数有界因素扰动下脉冲系统的渐近稳定性。采用比较系统法,以Lyapunov函数为媒介,利用扰动R(t,x(t))的控制量,对能判断系统(1)渐近稳定的比较原理和比较系统进行调整,建立了能够判断系统(2)渐近稳定的比较原理和比较系统,通过分析比较系统的渐近稳定性,得到系统(2)渐近稳定的充分条件,简化了分析过程,为解决这类问题提供了一种新方法。本文方法对扰动项的适用范围较窄,未来可尝试放宽对扰动项的限制,使其适用于范围更广的系统;另外,本文只考虑了系统描述函数具有扰动的情况,未来可尝试研究系统描述函数与脉冲量函数均具有扰动的脉冲系统。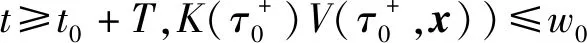
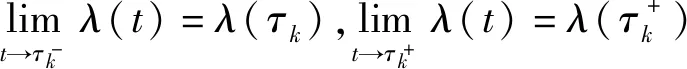
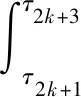
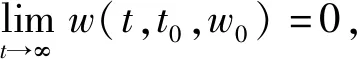
2 渐近稳定性条件
3 结 论

