路径直积图的意大利控制数

高 红，黄佳欢，栗 坤，杨元生

（1.大连海事大学理学院，辽宁 大连 116026；2.大连理工大学计算机科学与技术学院，辽宁 大连 116024）

在图G=(V，E)中，V表示顶点的集合，E表示边的集合。顶点v∈V的开邻域是与v有边相连的顶点构成的集合，即N(v)={u|u是顶点且(uv)∈E}。N(v)中包含的顶点的个数称为顶点v的度，记为deg(v)。图G的最小度和最大度分别记为δ和Δ。图G顶点的个数称为图G的阶。Pn表示阶为n的路径图。

图的罗马控制起源于古罗马帝国的军事防御问题［1］。古罗马帝国的每个城市最多能安置2支军队驻守。对于没有军队驻守的城市，其相邻的城市中必须至少有一个城市安置2支军队驻守，以便在该城市受到侵犯时相邻的城市能派出1支军队来支援。在这种历史背景下产生了图的罗马控制，定义为：在图G=(V，E)中，f为从顶点集合V到数集{0，1，2}的函数，如果每一个函数值为0的顶点v都至少与一个函数值为2的顶点相邻，则f为图G的罗马控制函数。f的权重图G的所有罗马控制函数权重的最小值称为图G的罗马控制数，记为γR(G)。关于罗马控制的相关研究结果可以参考文献［2-5］。

意大利控制［6］是罗马控制的一种变形，也称为罗马｛2｝-控制［7］或弱｛2｝-控制［8］，定义为：设图G=(V，E)，函数f∶V→{0，1，2}，如果每一个函数值为0的顶点v都至少与一个函数值为2的顶点相邻或者至少与2个函数值为1的顶点相邻，那么f称为图G的意大利控制函数。f的权重权重的最小值称为图G的意大利控制数，记为γI(G)。若f满足w(f)=γI(G)，则称f为图G的γI-函数。

意大利控制是图的控制理论中较为活跃的研究课题，吸引了很多学者。文献［6］中研究了意大利控制数与罗马控制数、彩虹控制数、经典控制数的关系，并证明了任意图的意大利控制数都小于等于其2-彩虹控制数。文献［7］中研究了树图T的意大利控制数，确定了分别满足γ(T)+1=γI(T)和2γ(T)=γI(T)的树图的特点，其中γ(T)是树图的控制数。文献［8］中给出了圈Cn与C5的笛卡尔乘积Cn□C5的意大利控制数下界，并确定了Cn□C3和Cn□C4意大利控制数的精确值。文献［9］中确定了广义彼得森图P(n，3)意大利控制数的精确值。文献［10］中研究了有向圈乘积图的意大利控制数。文献［11］中研究了有根乘积图的意大利控制数。学者们还研究了与意大利控制相关的全局意大利控制［12］、独立意大利控制［13］、完美意大利控制［14-16］、符号意大利控制［17］、全意大利控制［18］、外独立意大利控制［19］、限制意大利控制［20］、安全意大利控制［21］等。

直积图，也称为克罗内克乘积图，是一种重要的图类，在实际中应用广泛，如在计算机通信网络、多处理器管理等领域。文献［22-23］中分别研究了直积图上的经典控制和完美控制。对于给定的2个图G和H，它们的直积图G×H=(V，E)，其中顶点的集合为V(G×H)={(u，v)|u∈V(G)，v∈V(H)}，边 的 集 合 为E(G×H)={(u1，v1)(u2，v2)|u1u2∈E(G)，v1v2∈E(H)}。

本研究中确定了Pn×P1、Pn×P2和Pn×P3意大利控制数的精确值，并给出了Pn×Pm(m≥4)意大利控制数的界。

以下是与本研究相关的定理：

定 理1［7］若 图G为 路 径 图Pn，则γI(G)=

定 理2［7］若 图G为 连 通 图，则γI(G)≥

1 Pn×P1和Pn×P2意大利控制数

Pn×P1是n个孤立点，因此可知Pn×P1的意大利控制数为n，即：

定理3对于任意的正整数n≥1，γI(Pn×P1)=n。

由于Pn×P2与2条不相交的路径图Pn是同构的，因此γI(Pn×P2)=2γI(Pn)。由定理1，可得以下定理：

定理4令G=Pn×P2，则

2 Pn×P3意大利控制数

2.1 Pn×Pm意大利控制数的上界

通过构造路径直积图的意大利控制函数可以得到γI(Pn×Pm)(m≥3)的上界。

定理5对于任意的正整数m≥3，n≥m，k≥2，有：

证明：设G=Pn×Pm的顶点集合为V={vi，j|0≤i≤n-1，0≤j≤m-1}，其中i是顶点的行标号，j是顶点的列标号。

（1）当m=3k时，按照下式构造意大利控制函数f：

图1显示了P7×P6上的意大利控制函数f，其中Rn(Rm)表示随着n(m)的增长，重复相应的1行（3列）。图1中，空心圆圈表示f(vi，j)=0的顶点，黑色实心点表示f(vi，j)=1的顶点，较大的粗边空心圆圈表示f(vi，j)=2的顶点。

图1 P7×P6上的意大利控制函数fFig.1 Italian dominating function f on P7×P6

（2）当m=3k-1时，分2种情况构造意大利控制函数f。

当n为偶数时，

当n为奇数时，

图2显示了P6×P5和P7×P5上的意大利控制函数f，其中Rn(Rm)表示随着n(m)的增长，重复相应的2行（3列）。

图2 P6×P5和P7×P5上的意大利控制函数fFig.2 Italian dominating function f on P6×P5 and P7×P5

（3）当m=3k-2时，分3种情况构造意大利控制函数f。

当n≡0(mod 3)时，

当n≡1(mod 3)时，

当n≡2(mod 3)时，

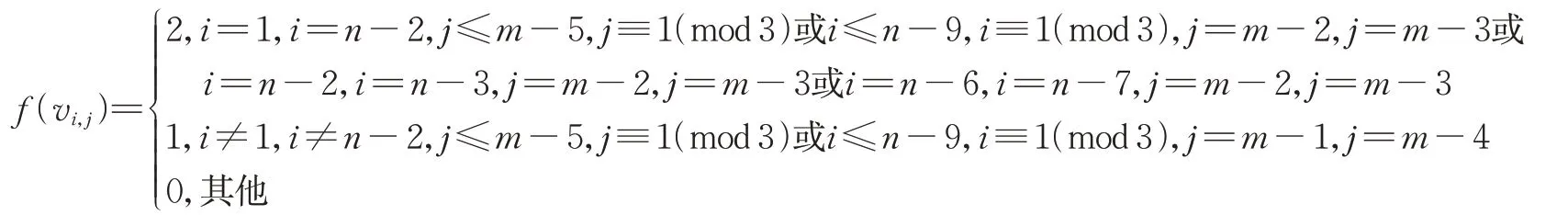
图3显示了P9×P7、P10×P7和P14×P7上的意大利控制函数f，其中Rn(Rm)表示随着n(m)的增长，重复相应的3行（3列）。

可以验证，按照以上方式构造的f均为意大利控制函数。根据f的定义并结合图示，可以计算得到f的权重，如下所示：

因此，可得

即：

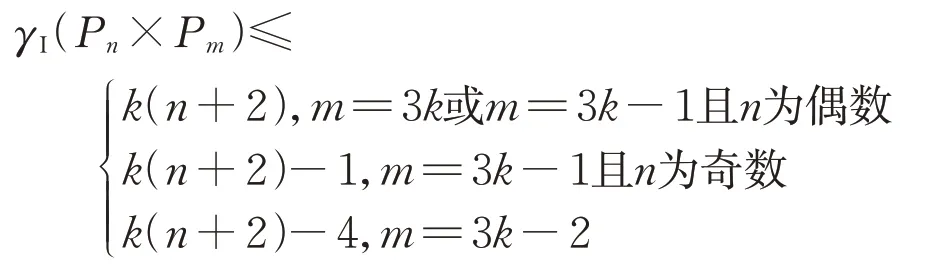
根据定理5，可以得到Pn×P3意大利控制数的上界，即有以下的推论：

推论1对于任意的正整数n≥3，γI(Pn×P3)≤n+2。

2.2 Pn×P3意大利控制数的下界

本节中证明Pn×P3意大利控制数的下界也是n+2。令G=Pn×P3，顶 点 集V(G)={vi，j|0≤i≤n-1，0≤j≤2}，f是G上的意大利控制函数，记Vi={vi，j|0≤j≤2}(0≤i≤n-1)，fi=f(Vi)=

引理1在图Pn×P3中，若f为Pn×P3的意大利控制函数，则以下结论均成立：

（1）若fi=0(1≤i≤n-2)，则fi-1+fi+1≥4。

（2）若f0=0，则f1≥4；若f0=1，则f1≥2；若f0=2，则f1≥2。若fn-1=0，则fn-2≥4；若fn-1=1，则fn-2≥2；若fn-1=2，则fn-2≥2。

（3）f0+f1≥3；若f0=1，f1≤3，则f2≥1。fn-1+fn-2≥3；若fn-1=1，fn-2≤3，则fn-3≥1。

（4）f0+f1+f2≥4，fn-1+fn-2+fn-3≥4。

（5）fi-1+fi+fi+1≥3(2≤i≤n-3)。

证明：（1）若fi=0(1≤i≤n-1)，有f(vi，0)=f(vi，1)=f(vi，2)=0，则

由fi-1+fi+1≥4可 知，若fi-1=0，1，2，3，则fi+1≥4，3，2，1；若fi-1≥4，则fi+1≥0。因此，fi-1和fi+1要么满足fi-1=2且fi+1≥2，要么满足fi-1≥3或fi+1≥3。

（2）若f0=0，则

若f0=1，则f(v0，0)和f(v0，2)中至少有一个等于0，所以f(v1，1)=2，即f1≥2。若f0=2，则f(v0，0)、f(v0，1)和f(v0，2)中 至 少 有 一 个 等 于0，所 以 有f(v1，1)=2或者f(v1，0)+f(v1，2)≥2，即有f1≥2。

同理可得，若fn-1=0，则fn-2≥4；若fn-1=1，则fn-2≥2；若fn-1=2，则fn-2≥2。

（3）当f0≥3时，显 然 有f0+f1≥3。当f0＜3时，由本引理第2条结论，即由（2）可知，f0+f1≥3，并且由（2）的证明可知，若f0=1，则f(v1，1)=2。若f1≤3，则f(v1，0)和f(v1，2)中至少有一个等于0。由于f0=1，根据意大利控制函数的定义，f2≥1。

同理可得，fn-1+fn-2≥3；若fn-1=1，fn-2≤3，则fn-3≥1。

（4）根据本引理的（2）和（3），有f0+f1+f2≥4，fn-1+fn-2+fn-3≥4。

（5）若fi=0，由本引理（1）可知，fi-1+fi+1≥4，所以fi-1+fi+fi+1≥3。若fi=1或2，则f(vi，0)、f(vi，1)和f(vi，2)中至少有一个为0，故f(vi-1，1)+f(vi+1，1)≥2或f(vi-1，0)+f(vi-1，2)+f(vi+1，0)+f(vi+1，2)≥2，故fi-1+fi+fi+1≥3。

定理6γI(P3×P3)=4。

证明：在图P3×P3中构造意大利控制函数f：f(v1，0)=f(v1，2)=1，f(v1，1)=2，其他顶点f(vi，j)=0。f为意大利控制函数且f的权重w(f)=4，所以γI(P3×P3)≤4。根据引理1（4）可知f0+f1+f2≥4，所以γI(P3×P3)=4。

定理7对于任意的正整数n≥4，γI(Pn×P3)≥n+2。

证明：在图G=Pn×P3中，顶点集合V(G)={vi，j|0≤i≤n-1，0≤j≤2}，Vi={vi，j|0≤j≤2}(0≤i≤n-1)，f为Pn×P3的γI-函数，fi=f(Vi)=

由引理1（3）、（4）、（5）可知，f0+f1≥3，fn-1+fn-2≥3，f0+f1+f2≥4，fn-1+fn-2+fn-3≥4，fi-1+fi+fi+1≥3(2≤i≤n-3)。

当n≡0(mod 3)时，

当n≡1(mod 3)时，

当n≡2(mod 3)时，

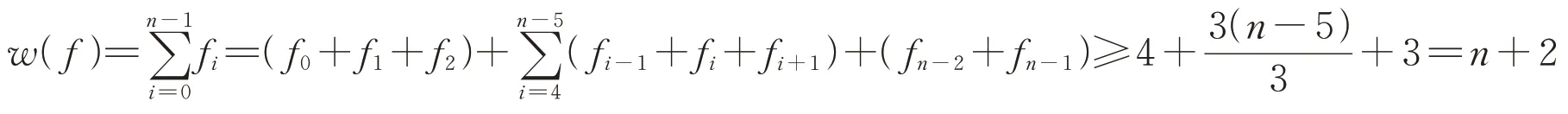
综上，γI(Pn×P3)≥n+2。

由推论1和定理7，可以得到以下定理：

定理8对于任意的正整数n≥4，γI(Pn×P3)=n+2。

3 Pn×Pm（m≥4）意大利控制数的界

由于Δ(Pn×Pm)=4且|V(G)|=mn，因此根据定理2可以得到推论2。

推论2若G=Pn×Pm，则

由定理5和推论2可以得到定理9。

定理9对于任意的正整数m≥4且n≥m，有：

4 结语

研究了路径直积图Pn×Pm的意大利控制数，确定了一些路径直积图的意大利控制数，γI(Pn×P1)=n；当n≡1(mod 2)时，γI(Pn×P2)=n+1；当n≡0(mod 2)时，γI(Pn×P2)=n+2；γI(P3×P3)=4；γI(Pn×P3)=n+2(n≥4)。对于m，n≥4，利用可递推的方法构造了Pn×Pm的意大利控制函数，从而给出了γI(Pn×Pm)的界。这种可递推的方法可以用于有任意多顶点的图类，实现用有限的方法解决无限的问题。

作者贡献声明：

高红：证明方法提出，算法总体设计，论文定稿。

黄佳欢：论文写作，画图，程序编写。

栗坤：论文初稿的写作，程序调试。

杨元生：方法指导，程序设计指导。