超导电动磁浮列车悬浮和导向特性

王小农，黄靖宇

（1.同济大学国家磁浮交通工程技术研究中心，上海 201804；2.同济大学道路与交通工程教育部重点实验室，上海 201804）

在新型轨道交通发展多样化的进程中，高速磁浮列车以转弯半径小、爬坡能力强、对环境友好等特点，成为最具竞争力的地面交通运输工具之一［1-6］。相对成熟的列车磁浮技术包括电磁悬浮（electromagnetic suspension，EMS）和 电 动 悬 浮（electrodynamic suspension，EDS）。EMS磁浮列车悬浮间隙较小（8～10 mm），其悬浮和导向系统采用主动控制［7-8］。超导电动磁浮列车作为EDS磁浮技术的一种，悬浮间隙较大（约100 mm），悬浮和导向系统采用被动控制。超导线圈无铁心、质量轻、磁场强、能耗低，并具备悬浮、导向、驱动的作用［9］，因此就超导电动磁浮列车相关技术展开分析。

日本山梨磁浮试验线以ML型电动磁浮列车为试验样车，通过安装在导轨上及车辆两侧的长定子直线电机驱动，车载超导线圈起励磁作用，轨道内侧线圈起电枢作用。悬浮力与导向力来自于车辆两侧，在导轨两侧的侧壁上排列着多组悬浮和导向绕组，车辆的超导磁场在导轨侧壁的短路绕组中产生感应电流和感应磁场，维持车体运行过程中的稳定悬浮和导向。ML型电动磁浮系统轨道结构的悬浮与导向绕组为“8”字形零磁通线圈，确保了不受牵引绕组的影响。导轨产生的悬浮和导向磁场为感应磁场，列车运行速度越高，悬浮力与导向力越大，当列车速度低于悬浮和导向临界速度时，超导磁浮车辆所产生的悬浮力和导向力较小，不足以支撑列车悬浮和导向，车辆依靠安装在转向架上的支撑车轮和导向车轮辅助运行。因此，开展超导电动磁浮列车的悬浮和导向特性研究，揭示超导线圈与轨道线圈之间的作用力关系，对于超导电动磁浮列车的稳定控制以及电动磁浮系统的结构设计和优化具有重要意义。

王志涛等［10］以日本MLX01型超导电动磁浮列车为研究对象，仅考虑了超导线圈与单个轨道线圈正对的情况，研究了电磁力随横向位移、悬浮位移的变化规律以及轨道线圈感应电流的形成机理。Cai等［11］探讨了MLX01型超导电动磁浮列车运行过程中影响系统稳定性的关键参数，并计算和分析了列车发生竖向位移和侧向位移时列车的相关特性，所建立的模型也仅考虑了转向架单侧的作用，未建立完整的磁浮列车转向架结构模型。电动磁浮列车利用电磁力实现推进、悬浮和导向，目前计算电磁力的常用方法是电磁场方法和电路方法，但大多数磁场计算有限元软件无法实现与运动相关的计算问题［5］，因此大多数学者选择电路元件来表示实际系统中的元件及其相对运动，以电路的方式模拟电磁系统或机电系统的瞬态和动态性能［12］。Say［13］采用电路理论分析了旋转电机的瞬态响应和稳态性能，Elliott［14］采用动态电路理论分析了电磁发射装置的瞬态和动态性能。加拿大磁悬浮研究团队采用动态电路理论计算了连续薄板的悬浮性能，并且将动态电路理论与谐波分析相结合，确定了连续薄板的瞬态及稳态性能［15-16］。因此，结合动态电路理论和磁场理论，建立超导电动磁浮列车单个转向架的场-路-运动耦合模型，开展MLX01型超导电动磁浮列车相关电磁关系及作用力关系的研究。

以MLX01型超导电动磁浮列车为研究对象，分析超导线圈与轨道线圈组成系统的电路一般表达式，并建立单个转向架与轨道线圈的场-路-运动耦合数值模型。随后，分析不同垂向位移和横向位移下超导线圈与轨道线圈之间作用力的关系特性，揭示无交叉连接与交叉连接“8”字形轨道线圈之间的关系，并研究列车运行过程中浮阻比与导阻比变化特性。

1 悬浮和导向系统一般电路数值模型

根据MLX01型超导电动磁浮列车地面轨道“8”字形零磁通线圈（下文简称“8”字形线圈）与超导线圈的位置结构关系，超导线圈与“8”字形线圈系统中的电流矩阵、电压矩阵、电感矩阵、电阻矩阵分别如下所示：

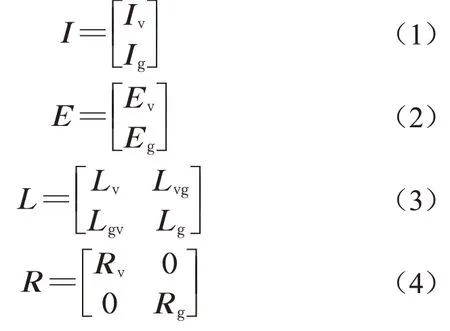
式中：Iv、Ev分别为超导线圈的电流和电压子矩阵；Ig、Eg分别为“8”字形线圈的电流和电压子矩阵；Lv、Lg分别为超导线圈和“8”字形线圈的电感子矩阵；Lvg和Lgv分别为超导线圈和“8”字形线圈的互感子矩阵；Rv、Rg分别为超导线圈和“8”字形线圈的电阻子矩阵。鉴于超导线圈的特性，式（4）中的Rv为零元素矩阵。定义变换矩阵，如下所示：

式中：Tv、Tg分别为超导线圈和“8”字形线圈电流和电压的变换子矩阵，其结构形式取决于线圈之间的连接方式。若仅“8”字形线圈的连接方式发生变化而超导线圈的结构不发生变化，则Tv为单位对角阵。

基于能量守恒定律，变换后系统的电流、电压表达式以及变换后系统的电感矩阵、电感变化率矩阵和电阻矩阵表达式分别如下所示：

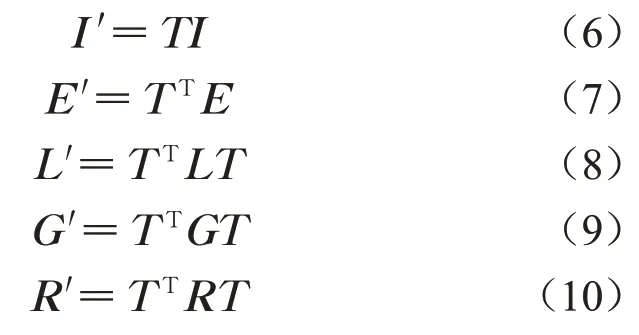
式中：I和I′分别为系统变换前后的电流矩阵；E和E′分别为系统变换前后的电压矩阵；L和L′分别为系统变换前后的电感矩阵；G和G′分别为系统变换前后的电感变化率矩阵；R和R′分别为系统变换前后的电阻矩阵。基于超导电动磁浮列车系统电路相关参数表达式，假设在超导电动磁浮车辆一侧由m个超导磁体（SCM）与n个“8”字形线圈相互作用而产生悬浮力和导向力，其中n个“8”字形线圈包括2n个线圈，上部线圈从1到n编号，下部线圈从n+1到2n编号。超导电动磁浮列车单个转向架与“8”字形线圈结构如图1所示。

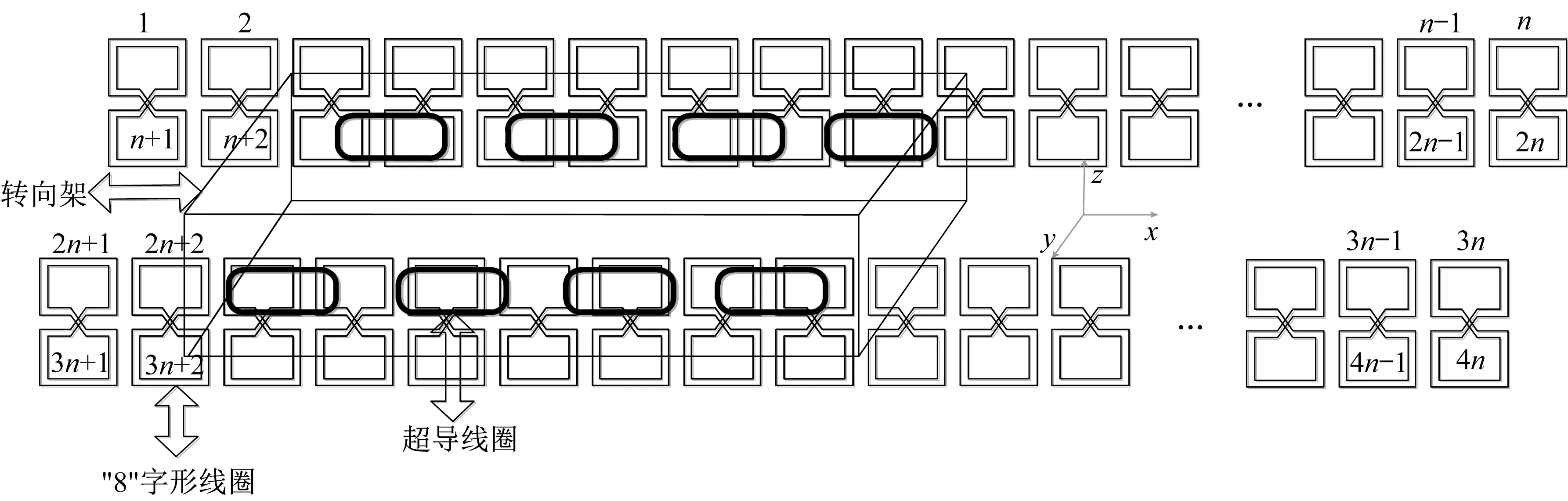
图1 超导电动磁浮列车单个转向架与“8”字形线圈Fig.1 Single bogie and figure-eight-shaped coil of superconducting electrodynamic maglev train

根据基尔霍夫电压定律，超导高速磁浮系统的电压方程如下所示：

超导电动磁浮列车运行过程为三维运动，采用vx、vy、vz分别表示车辆在x、y、z方向上的运行速度，将式（11）转化为以下形式的动态电压方程：

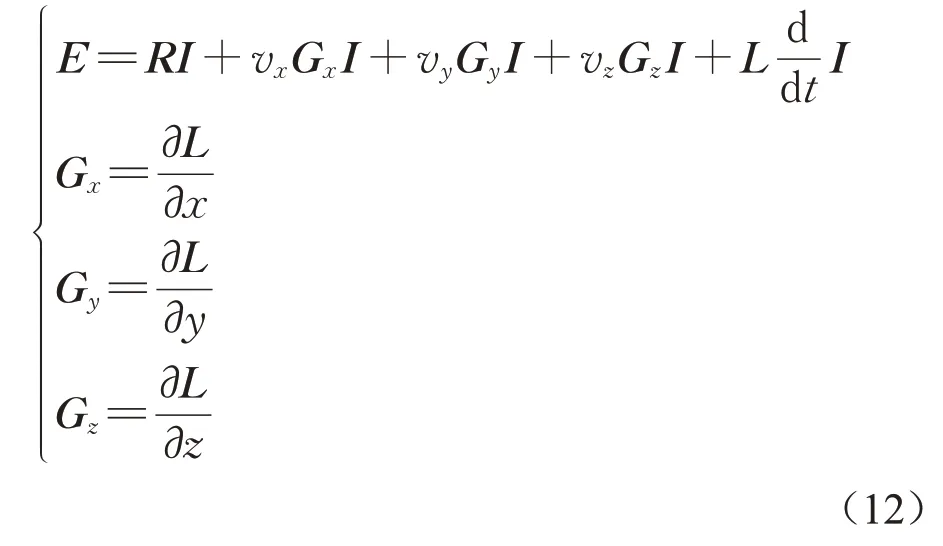
根据能量法，超导磁浮系统中作用在车辆上的3个力分量fx、fy及fz表达式如下所示：

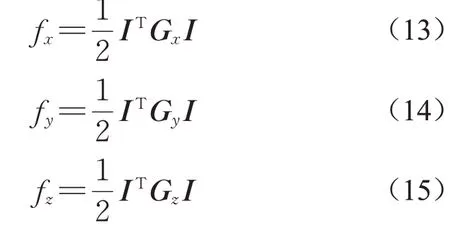
式中：fx为超导磁浮系统运行方向产生的推进力；fy为超导磁浮系统水平方向的导向力；fz为超导磁浮系统竖直方向的悬浮力。

2 超导电动磁浮列车动态电路模型

2.1 无交叉连接“8”字形线圈电路模型

无交叉连接“8”字形线圈与超导线圈结构模型如图2a所示，电路简化模型如图2b所示。

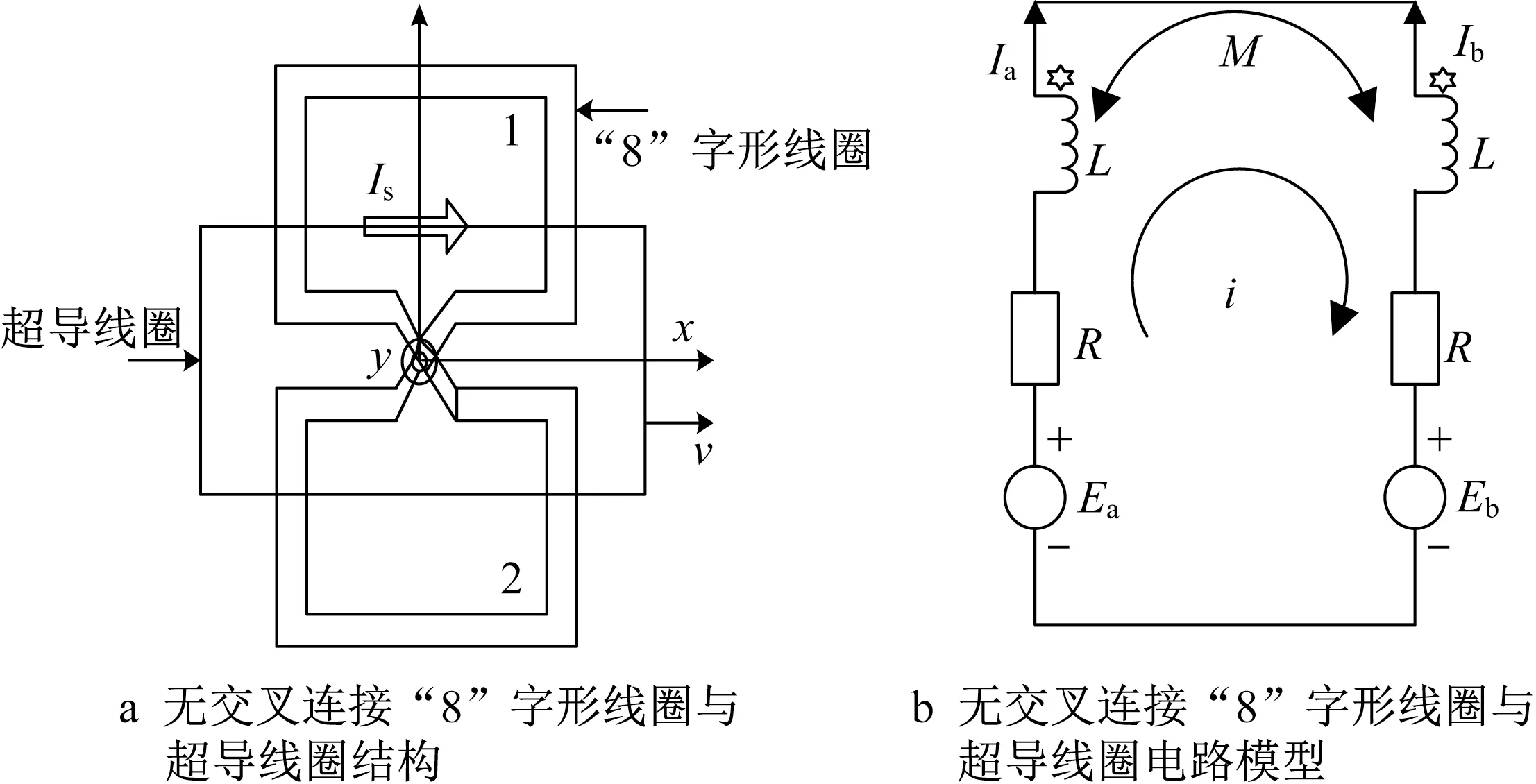
图2 无交叉连接“8”字形线圈与超导线圈结构和电路模型Fig.2 Structure and circuit model of non-cross connection figure-eight-shaped coil and superconducting coil

每个分支具有电阻R和电感L，代表8”字形线圈的单个环路。上下回路之间的互感为M，移动超导磁体和“8”字形线圈的上下回路之间的耦合分别由电压Ea和Eb表示。Ea、Eb的表达式以及系统电压方程如下所示：

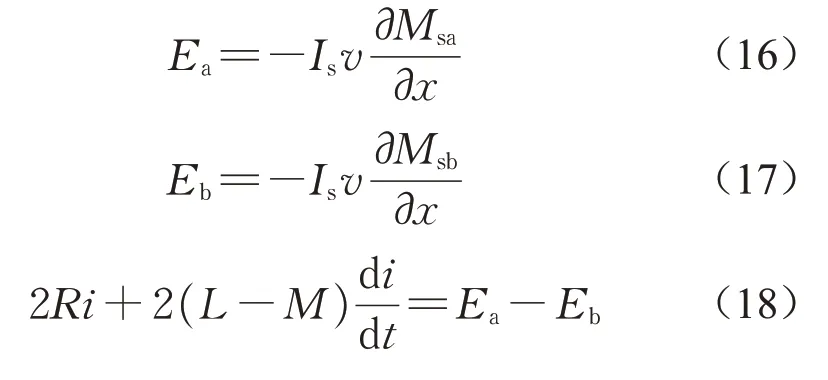
因此，由式（13）、（14）、（15）可得超导线圈所受电磁力fx、fy及fz的表达式，如下所示：

式（16）―（21）中：Is和v分别为超导线圈的电流和速度；Msa和Msb分别为超导线圈与“8”字形线圈上下回路之间的互感；i为“8”字形线圈中循环的电流；Ia和Ib分别为在上下环路中流动的电流。

2.2 交叉连接“8”字形线圈电路模型

超导线圈与安装在导轨两侧的交叉连接“8”字形线圈结构模型如图3a所示，电路模型如图3b所示。回路1和2之间的互感与回路3和4之间的互感均为M。Ij（j=a，b，c，d）和Ej（j=a，b，c，d）分别为环路中的流动电流和感应电压，电路中流动的网状电流分别为i1、i2和i3，其中i2为穿过导轨的交叉连接电缆中的电流，实现超导磁浮系统导向功能。回路3和4中的感应电压分别为Ec和Ed，超导线圈与回路3和4之间的互感分别为Msc和Msd表示，关系式如下所示：

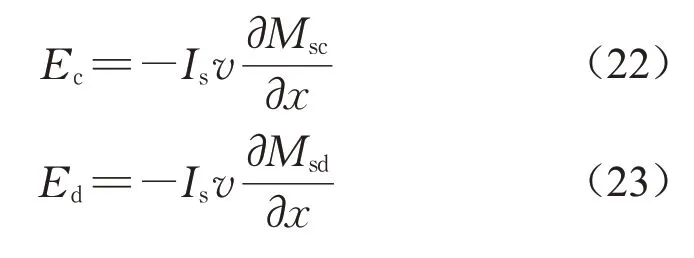
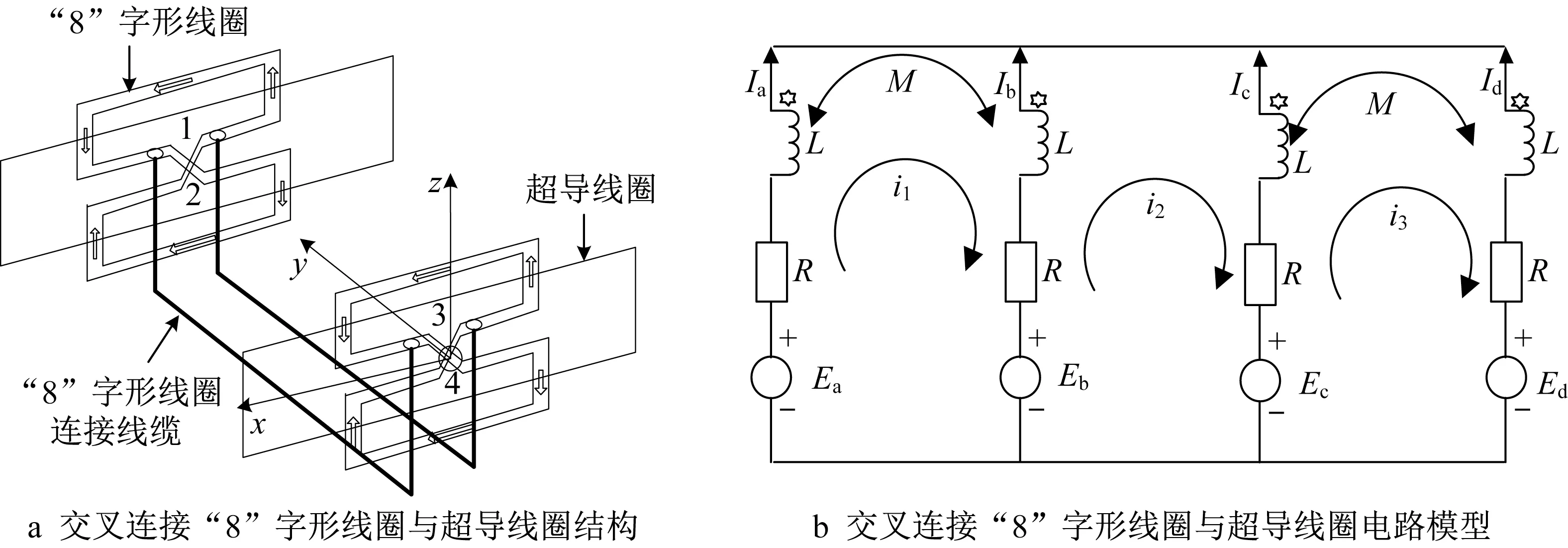
图3 交叉连接“8”字形线圈与超导线圈结构和电路模型Fig.3 Structure and circuit model of cross connection figure-eight-shaped coil and superconducting coil

根据基尔霍夫电压定律，如图3b所示网格电压方程如下所示：

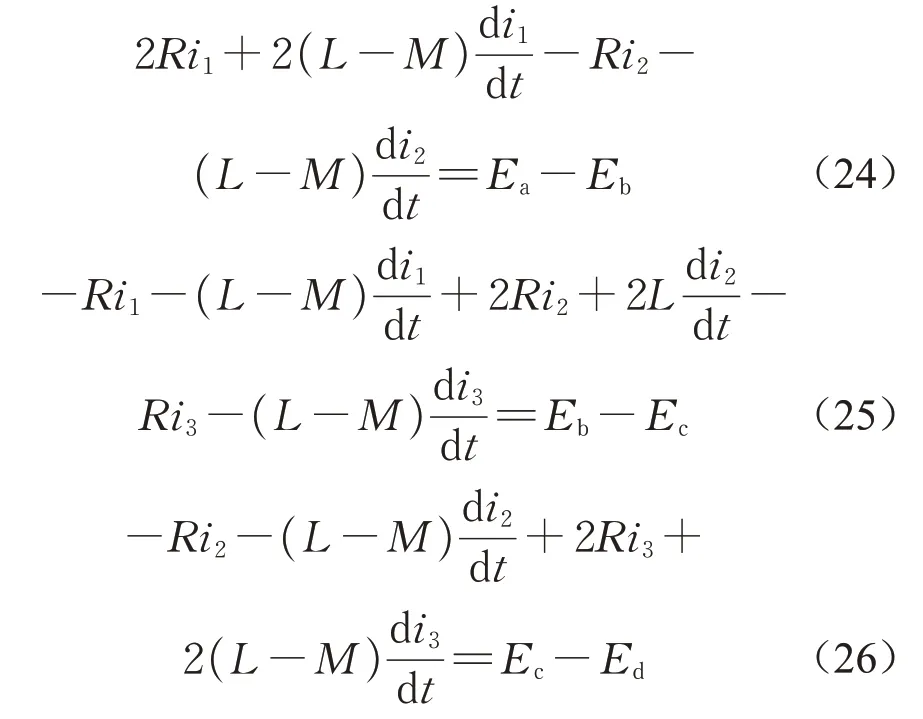
求解方程（24）―（26），超导电动磁浮列车运行过程中超导线圈所受电磁力的3个分量表达式如下所示：

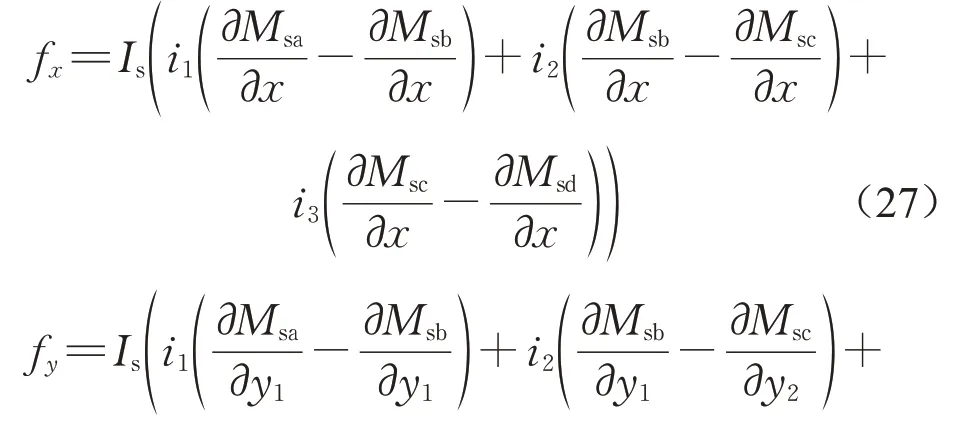
式中：y1与y2分别为超导电动磁浮列车运行时超导线圈两侧与轨道侧壁之间的横向位移。由式（27）―（29）可知，交叉连接“8”字形线圈悬浮和导向结构的电磁力分量取决于“8”字形线圈之间流动的电流。当超导电动磁浮列车处于轨道中心位置时，交叉连接“8”字形线圈的悬浮和导向系统成为2个无交叉连接“8”字形线圈，并且列车运行过程中所受到的电磁力由两部分组成，一部分是由交叉连接“8”字形线圈产生的，另一部分是由单个“8”字形线圈和气隙差异形成的。

3 超导电动磁浮列车悬浮和导向特性分析

以MLX01型超导电动磁浮列车为例进行悬浮和导向特性分析，相关参数如表1所示［10］。由第2节知，悬浮和导向系统结构各方向所受的电磁力与超导线圈和“8”字形线圈各环之间的互感及其不同方向的互感变化率有关，因此根据聂以曼公式计算超导线圈与“8”字形线圈之间的互感［17］。结合无交叉连接“8”字形线圈电路模型和交叉连接“8”字形线圈电路模型，建立单个转向架的场-路-运动耦合数值模型，并采用Matlab编写该模型仿真程序。

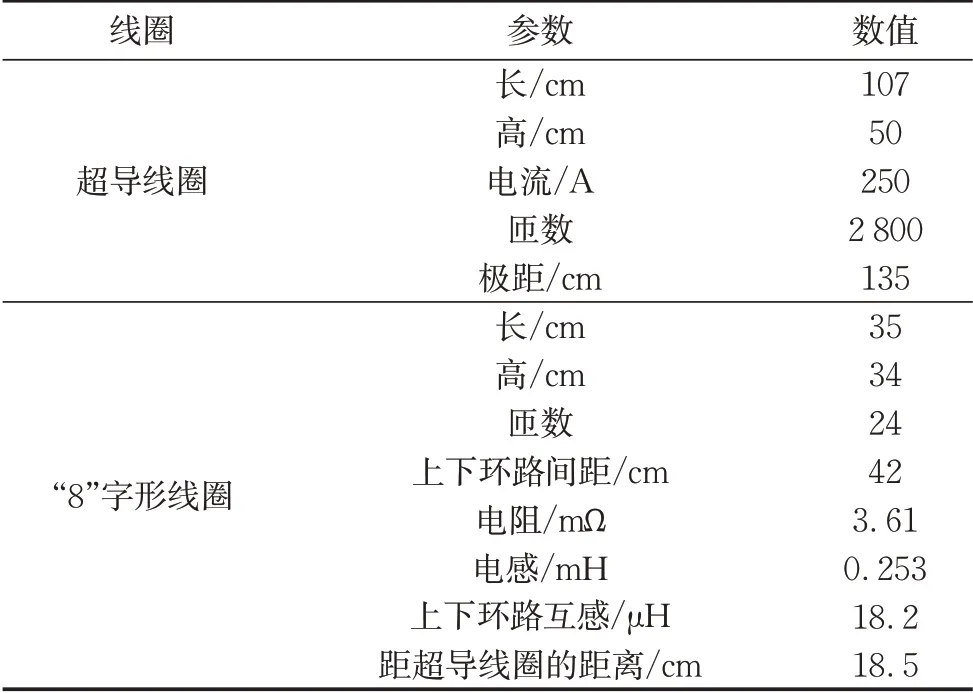
表1 MLX01型超导电动磁浮列车参数Tab.1 Parameters of superconducting electrodynamic maglev train of MLX01 type

3.1 单个转向架的场-路-运动耦合模型及数值验证

MLX01型超导电动磁浮列车悬浮和导向系统受力分析如图4所示，其中fpq(p=x，y，z，q=R，L)表示不同方向左右两侧的受力。文献［18］中对日本山梨磁浮试验线“8”字形线圈无交叉连接时转向架单侧的悬浮力和导向力进行了现场测量试验，因此本研究中采用现场实测数据验证单个转向架场-路-运动耦合数值模型的正确性。采用单个转向架的场-路-运动耦合数值模型，对不同时速下的垂向力、纵向力以及侧向力进行计算，并将速度为150、200、250、300 km·h-1下的垂向力、纵向力以及侧向力与山梨试验线实测数据进行对比，如图5～7所示。可以看出，在忽略现场实测数据和单个转向架数值模型误差的基础上，本模型计算值与山梨试验线实测值基本吻合，验证了本模型的正确性。

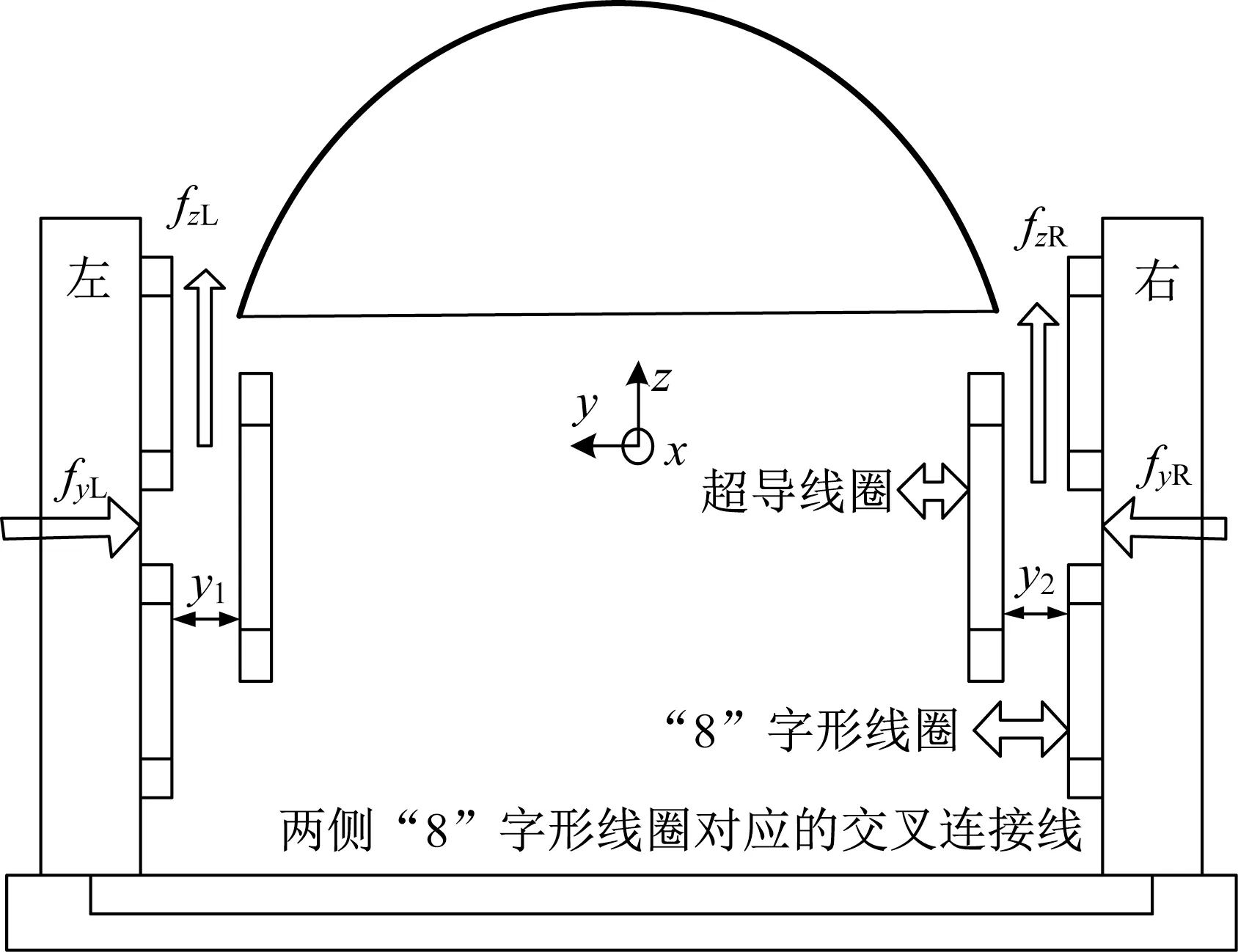
图4 悬浮和导向系统受力分析Fig.4 Force analysis of levitation and guidance system

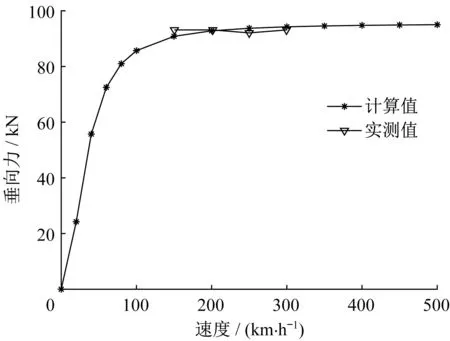
图5 垂向力计算值与实测值对比Fig.5 Comparison between calculated value and measured value of vertical force

3.2 超导电动磁浮列车悬浮和导向特性分析

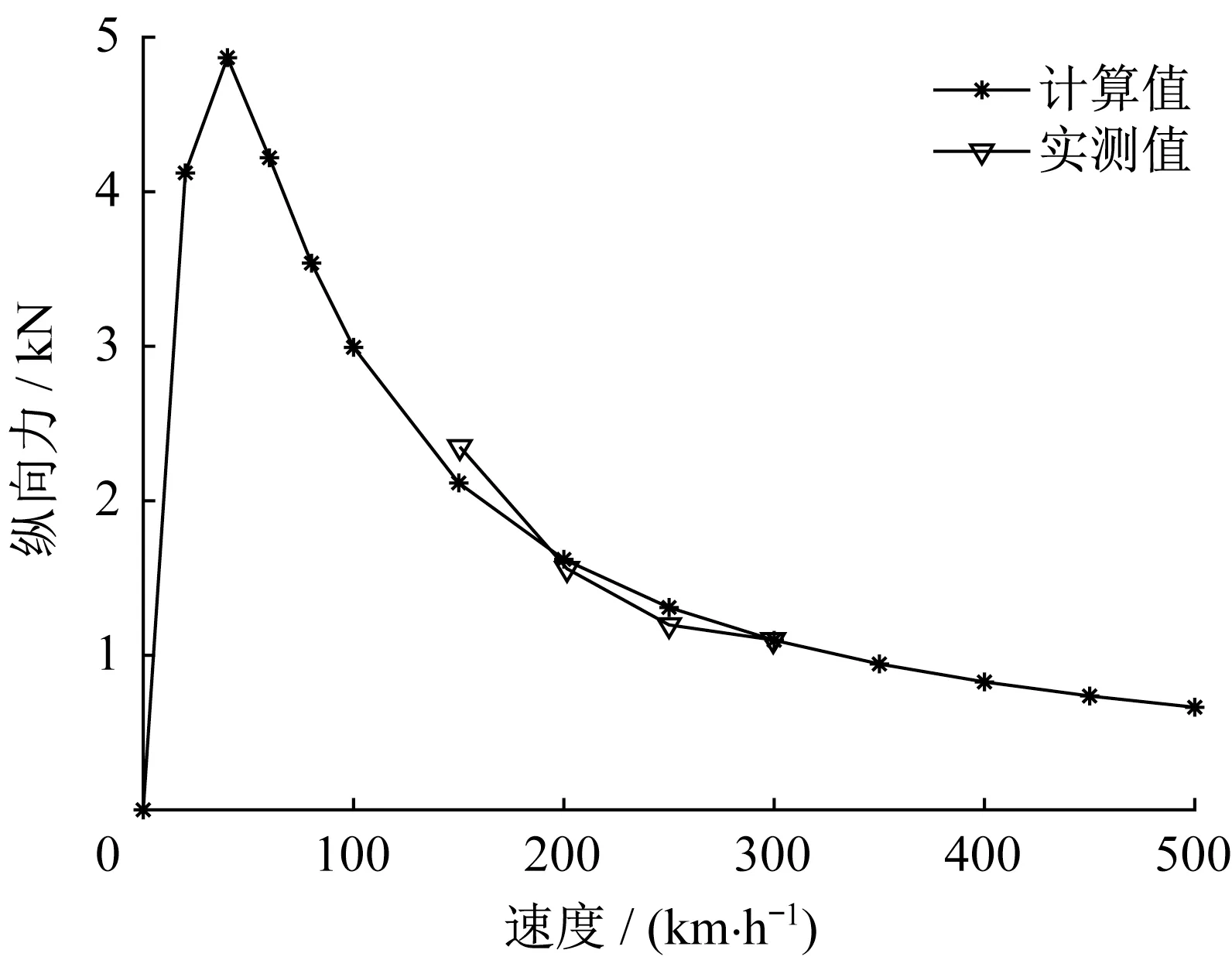
图6 纵向力计算值与实测值对比Fig.6 Comparison between calculated value and measured value of longitudinal force

MLX01型超导电动磁浮列车处于轨道中心时，单侧超导线圈与“8”字形线圈之间的横向位移为18.5 cm。超导线圈与“8”字形线圈之间的位置关系以及垂向位移和横向位移定义如图8所示。假设左侧横向位移为13.5 cm，右侧横向位移为23.5 cm，转向架的垂向位移变化范围为0～15 cm，车辆速度为135 m·s-1。图9为转向架左右两侧悬浮力与垂向位移关系。从图9可以看出，MLX01型超导电动磁浮列车运行过程中悬浮力主要由无交叉连接下左右两侧“8”字形线圈提供，而交叉连接下悬浮力较小。同时，无交叉连接下左侧的悬浮力明显大于右侧的悬浮力，因此超导转向架会发生侧滚现象，影响列车的运行稳定性。图10为转向架左右两侧导向力与垂向位移的关系。当垂向位移为零时，无交叉连接下左右两侧的导向力均为零。图11为交叉连接与无交叉连接下导向力与垂向位移关系。由于两侧初始横向位移不相等，因此垂向位移为零时交叉连接“8”字形线圈提供导向力，大小为50 kN左右。当垂向位移小于5 cm时，无交叉连接下产生的导向力明显小于交叉连接下产生的导向力，但垂向位移大于5 cm时，无交叉连接下产生的导向力急剧增大，并且无交叉连接和交叉连接下在垂向位移为5 cm时导向力基本相等。在MLX01型超导电动磁浮列车运行过程中，垂向位移一般为1～4 cm，因此车辆正常运行时交叉连接下产生的导向力作为车辆导向的主要作用力。

图8 垂向位移与横向位移定义Fig.8 Definition of vertical displacement and lateral displacement

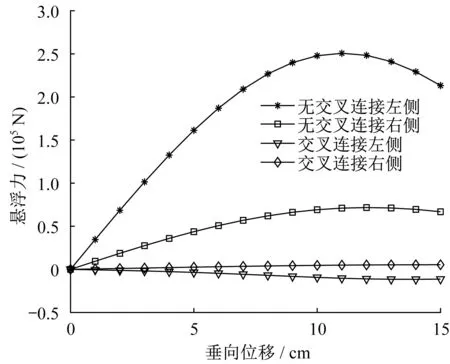
图9 交叉连接与无交叉连接下转向架左侧和右侧悬浮力与垂向位移关系Fig.9 Relationship between levitation force and vertical displacement under cross and non-cross connection on left and right sides of bogie

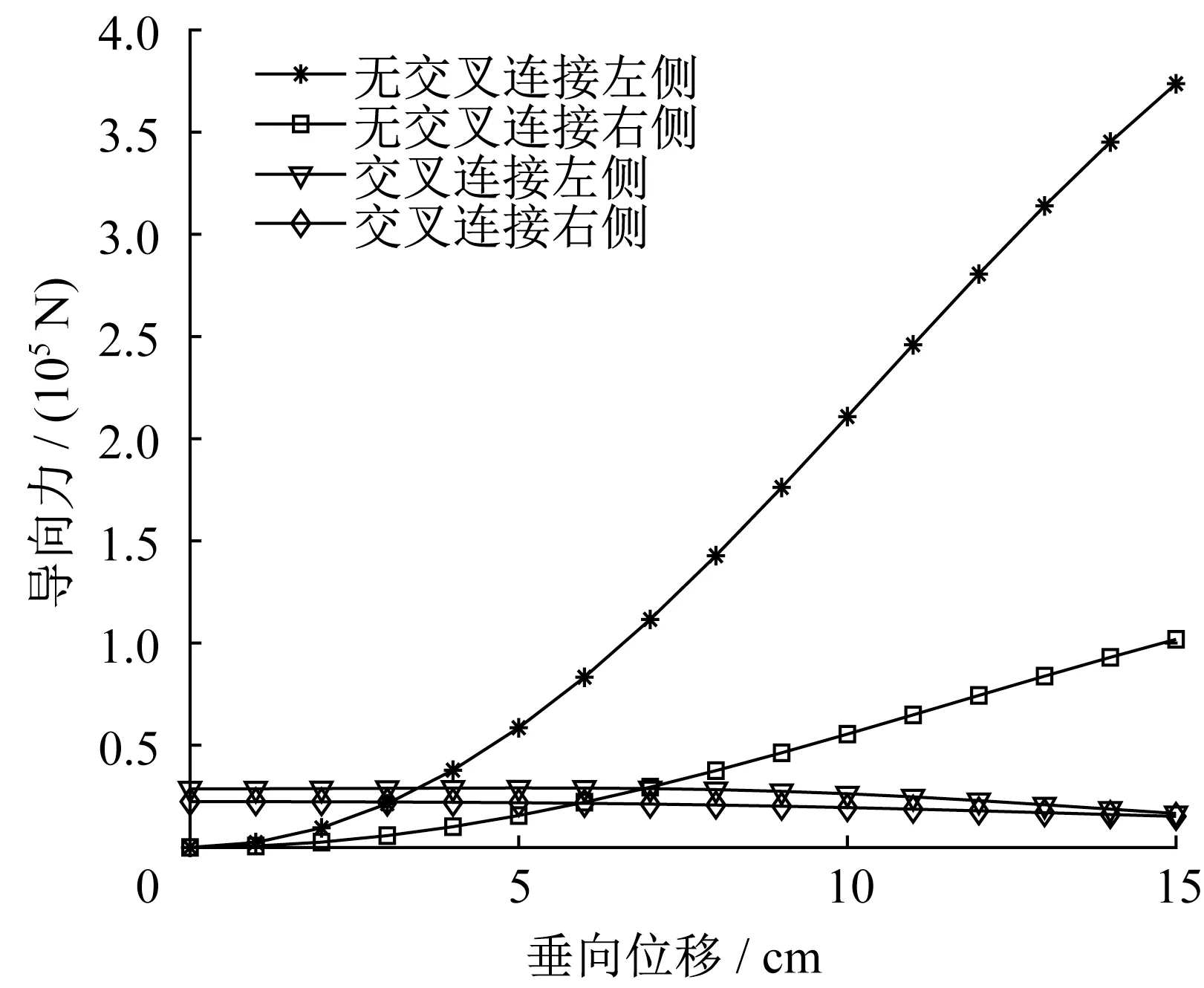
图10 交叉连接与无交叉连接下转向架左侧和右侧导向力与垂向位移关系Fig.10 Relationship between guidance force and vertical displacement under cross and noncross connection on left and right sides of bogie

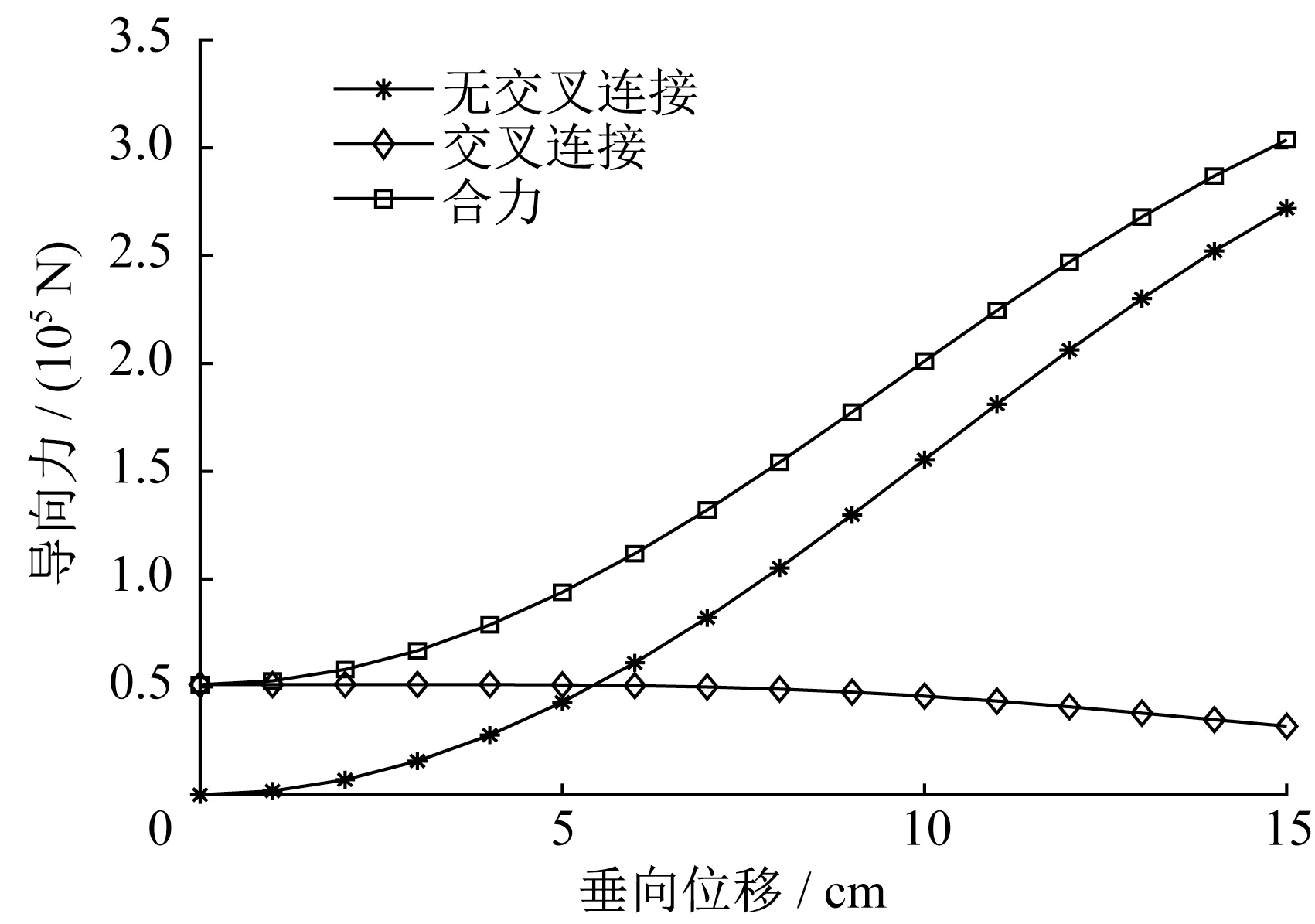
图11 交叉连接与无交叉连接下导向力与垂向位移关系Fig.11 Relationship between guidance force and vertical displacement under cross and noncross connection

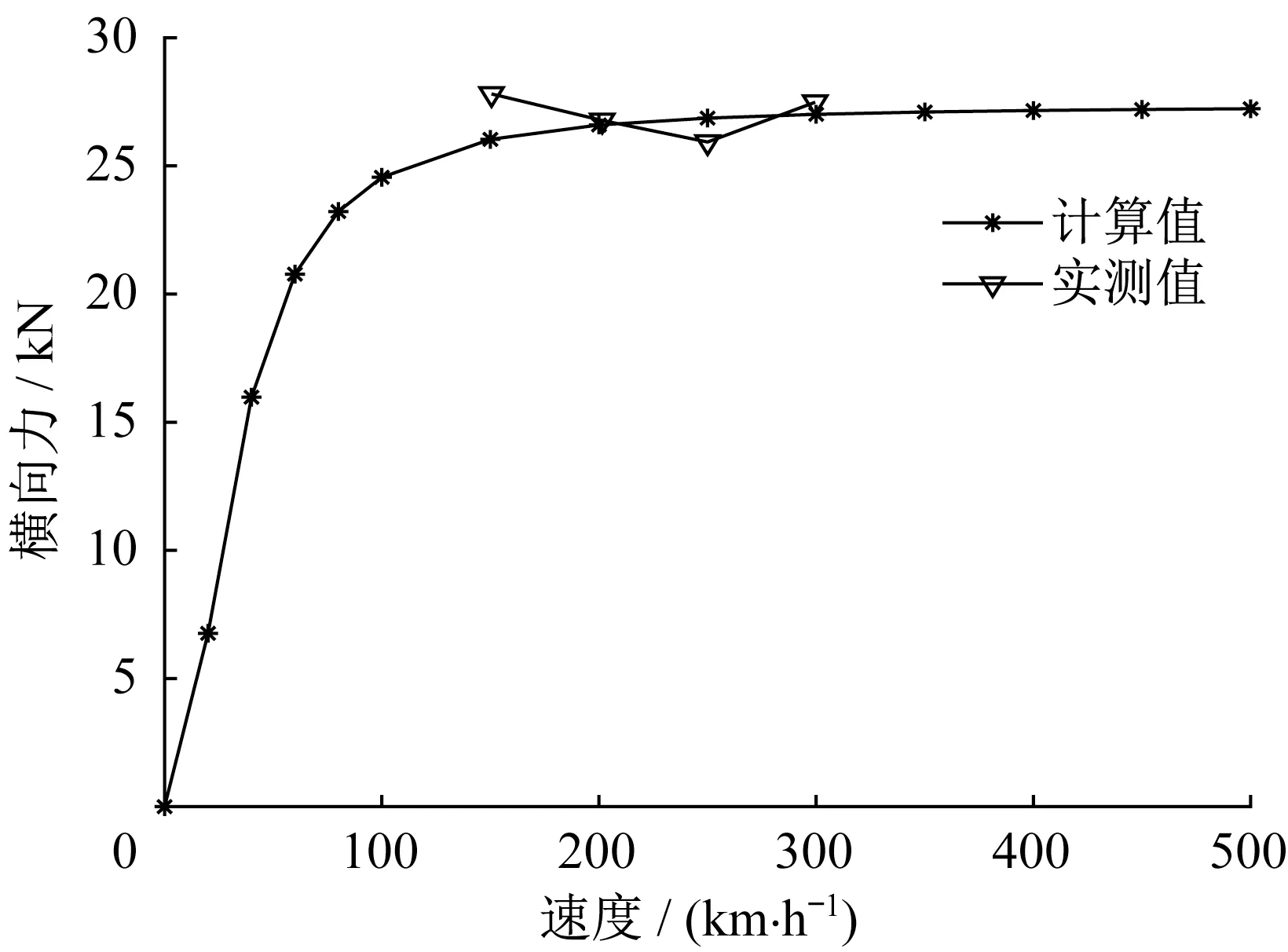
图7 横向力计算值与实测值对比Fig.7 Comparison between calculated value and measured value of transverse force

假设左侧横向位移变化范围为18.5～6.5 cm，右侧横向位移变化范围为18.5～30.5 cm，车辆垂向位移为5 cm。图12为交叉连接与无交叉连接下转向架左右两侧悬浮力与横向位移关系。由图12可知，随着横向位移的变化，交叉连接下产生的悬浮力基本趋近于零，车辆运行过程中的悬浮力主要由无交叉连接下产生的悬浮力提供，因此超导转向架会发生侧滚现象，影响列车的运行稳定性。图13为交叉连接与无交叉连接下转向架左右两侧导向力与横向位移关系。随着横向位移的变化，无交叉连接下左侧导向力逐步增大，右侧导向力逐步减小，交叉连接下左右两侧导向力均增大，并且左侧导向力增大速度大于右侧。图14为交叉连接与无交叉连接下导向力与横向位移关系。由图14可知，交叉连接下产生的导向力大于无交叉连接下产生的导向力，并且2种情况下导向力与横向位移成正比例关系。

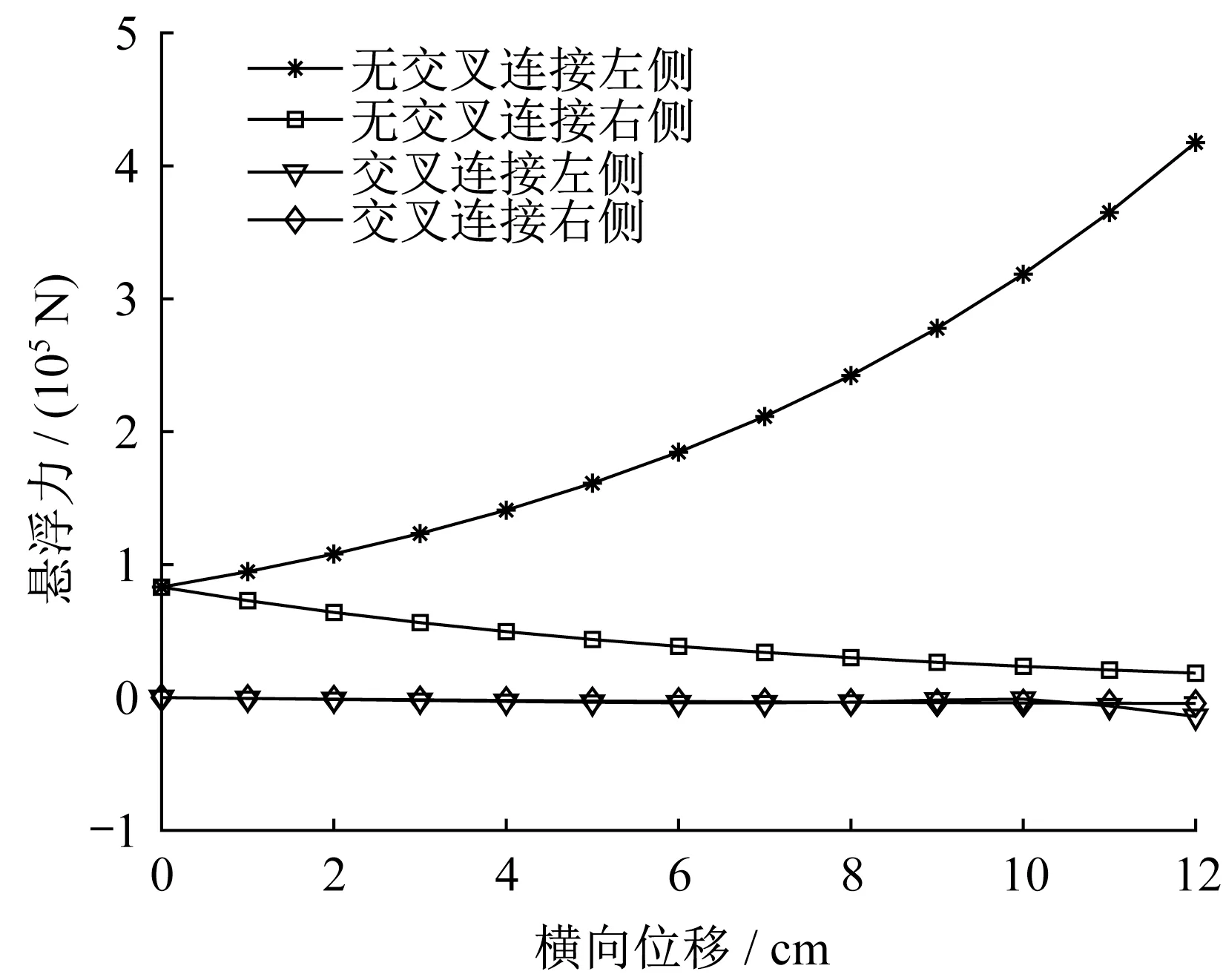
图12 交叉连接与无交叉连接下转向架左侧和右侧悬浮力与横向位移关系Fig.12 Relationship between levitation force and lateral displacement under cross and non-cross connection on left and right sides of bogie

图13 交叉连接与无交叉连接下转向架左侧和右侧导向力与横向位移关系Fig.13 Relationship between guidance force and lateral displacement under cross and non-cross connection on left and right sides of bogie

图14 交叉连接与无交叉连接下导向力与横向位移关系Fig.14 Relationship between guidance force and lateral displacement under cross and noncross connection

图15为当垂向位移5.0 cm时不同横向位移下的导阻比和浮阻比变化特性。当横向位移偏移为零时，浮阻比达到最大值108.718 6，并且浮阻比随着横向位移的增大而逐渐减小。当横向位移约为4.0 cm时，导阻比达到最大值53.63，并且随着横向位移的增大导阻比呈现先增大后减小的趋势。图16为当横向位移13.5 cm时不同垂向位移下导阻比和浮阻比变化特性。垂向位移为零时，浮阻比为零；当垂向位移为2.0 cm左右时，浮阻比达到最大值110.570 0；当垂向位移大于2.0 cm时，浮阻比随着垂向位移的增大而减小。同时，导阻比随着垂向位移的增大逐渐呈下降趋势。

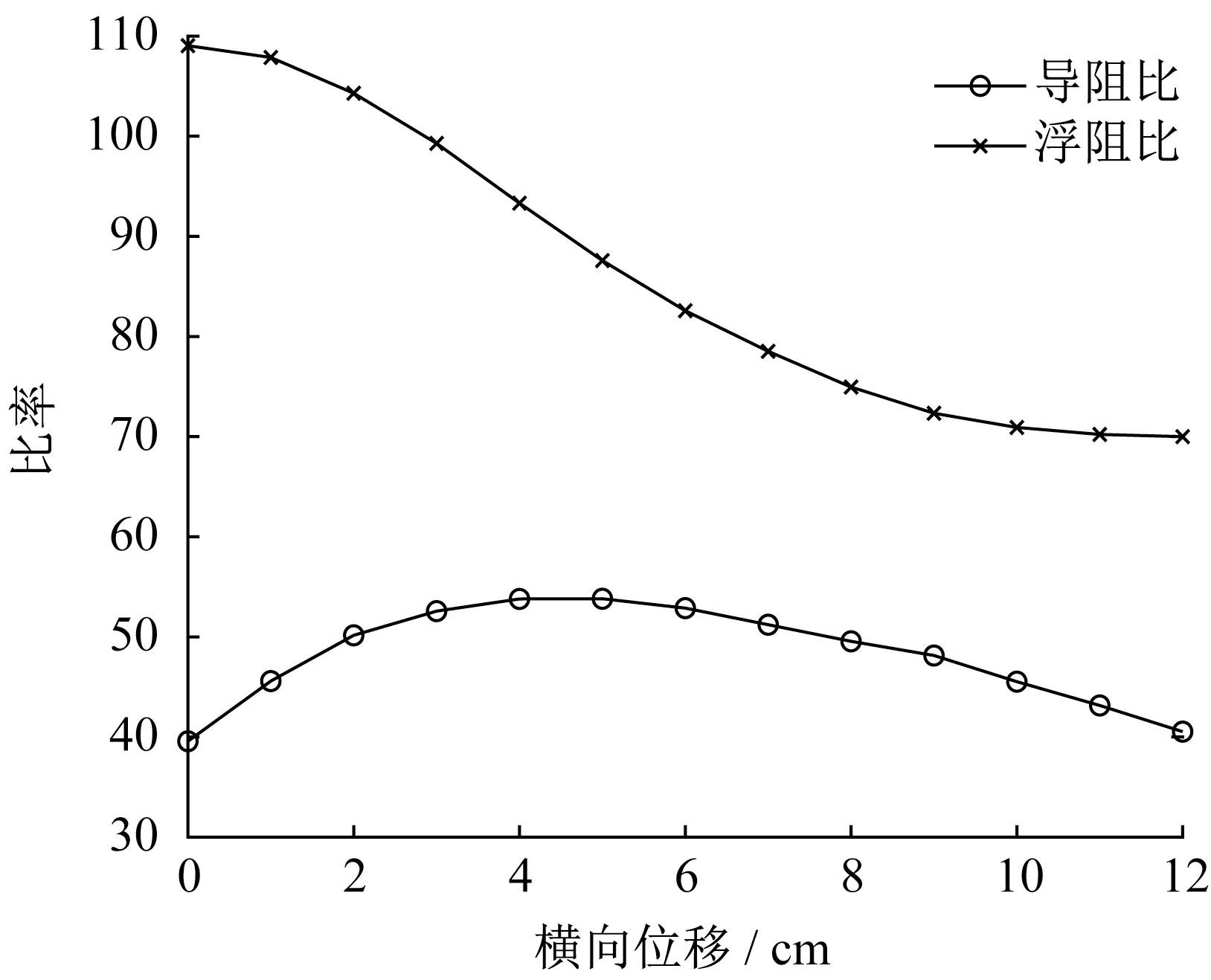
图15 导阻比和浮阻比与横向位移关系Fig.15 Relationship between guidance-drag ratio and lateral displacement and between levitation-drag ratio and lateral displacement

图16 导阻比和浮阻比与垂向位移关系Fig.16 Relationship between guidance-drag ratio and vertical displacement and between levitationdrag ratio and vertical displacement

4 结论

（1）MLX01型超导电动磁浮列车运行过程中悬浮力主要由无交叉连接下左右两侧“8”字形线圈产生，交叉连接下“8”字形线圈产生的悬浮力较小，并且列车偏离轨道中心时无交叉连接下左右两侧的悬浮力明显不等，因此转向架会发生侧滚现象，影响列车的运行稳定性。

（2）当垂向位移逐渐增大时，无交叉连接下产生的导向力明显小于交叉连接下产生的导向力，但随着垂向位移的增大，无交叉连接下产生的导向力急剧增大。车辆正常运行时垂向位移较小，因此交叉连接下产生的导向力作为车辆导向的主要作用力。

（3）随着横向位移的变化，无交叉连接下横向位移减小的一侧导向力逐步增大，另一侧导向力逐步减小，交叉连接下左右两侧导向力均增大，并且横向位移减小的一侧导向力增大速度大于另一侧。

（4）当横向位移为零时，浮阻比达到最大值，并且浮阻比随着横向位移的增大而逐渐减小，但导阻比随着横向位移的增大呈现先增大后减小的趋势。当垂向位移为零时，浮阻比为零，随着垂向位移的逐渐增大，浮阻比先增大后减小，导阻比随着垂向位移的增大逐渐减小.

作者贡献声明：

王小农：模型构建，程序编写，论文撰写。

黄靖宇：研究方向提出，学术指导，论文指导。