索网结构欧拉坐标找形法

刘 超，詹海鹏

（同济大学土木工程学院，上海 200092）

索网是由相互正交、曲率相反的2组拉索直接叠交而形成的一种负高斯曲率曲面结构［1］。索网的拉索一般采用由高强钢丝组成的钢绞线，通过拉索的轴向力抵抗外荷载作用，当拉索采用高强度材料时可以大幅减轻自重。索网结构能够比较经济地实现较大的跨度，目前已经成为大跨建筑的主要结构形式之一［2］。

索网结构不同于一般的刚性结构，施加预应力之前，结构形状是不稳定的，只有在适当的预应力作用下，结构才具有一定的刚度。刚性结构的一般分析方法是在已知结构形状的基础上进行的，而索网这种柔性结构，在对其结构受力分析之前，必须确定一定的边界和预应力条件下对应的结构形状，如何确定索网的平衡形状就是索网结构的找形问题。在设计实践中，结构的边界条件通常是已知的，需要通过特定的找形方法获得结构形状。早期，通过悬挂相应的结构模型或制造模型等物理方法寻找空间结构的形状［3-5］。随着计算机技术的发展，针对形状优化的研究主要集中于数值计算方法，力密度法［6-12］、动态松弛法［13-15］和有限元法［16］已经广泛应用于空间索网结构的找形。

1960年，Clough［16］提出了有限元法，而后各国学者均对有限元法进行了完善，目前该方法已经成为结构分析的有力工具。在索网结构找形问题中，有限元法应用较为广泛。有限元法大多直接采用已有的有限单元进行整体结构分析，包括两节点直线单元法、内插多节点单元法、样条函数单元法和两节点曲线单元法等［17-18］。有限元法的主要思路是根据平衡方程或能量原理推导刚度矩阵（弹性刚度矩阵与几何刚度矩阵），再计算力与位移的关系，最后集成整体平衡方程进行迭代计算。由于拉索的大位移特性，有限元法得到的平衡方程是非线性方程，迭代过程可能出现不收敛问题，因此需要不断调整初始线形和迭代参数。1965年动态松弛法被提出，该方法可用于索网找形分析。利用虚设的节点质量和运动阻尼，对节点施加激振力使之围绕平衡位置振动，整个体系经过平衡位置的瞬间动能最大、势能最小。因此，将平衡位置初速度设为零，这样整个体系的节点逐渐趋向于平衡位置，直到体系的动能小到可以忽略为止。动态松弛法的本质是利用特殊条件下的动力方法解决静力问题，与有限元法类似，在找形过程中同样会出现不收敛的情况。Schek［6］于1974年提出了用于索网找形分析的力密度法，并证明了力密度法可以求解无荷载索网的最小总长度。力密度法由于其简易的计算理念而得到快速发展，广泛应用于索网和膜结构设计中。王春江等［19］指出了力密度法矩阵组装的特点，编写了一维变带宽存储规则及其实现算法，并用C++语言编制了相应的计算程序。廖理等［20］提出了一种膜曲面离散的方法并将其作为索网划分初始网格的方法。韩大建等［21］构造了张拉索膜结构中的T单元来协调索和膜的变形，完善了索膜结构找形分析的力密度法。力密度法将几何非线性问题转化为线性问题，求解的是线性方程组，避免了非线性方程坐标初值不理想而导致迭代不收敛的问题，是求解空间结构找形问题的有效方法。

基于索网结构几何形状由力所决定的特点，提出了欧拉坐标找形法。利用静力平衡和几何协调关系，可以得到整个系统的平衡方程，然后建立力与节点坐标的线性关系。既可以将力作为初始参数求解相应的平衡状态，也可以将力密度作为描述力学平衡状态的参数，不同的力密度对应着不同的平衡状态。与力密度法相比，欧拉坐标找形法建立了更简单、更方便的拓扑关系，易于理解和计算。传统的力密度法只能针对固定节点的边界条件，而不能选择性地控制节点的三维坐标。欧拉坐标找形法能够在索网结构平面投影固定的条件下，无需复杂迭代就可以完成找形计算，有利于索网结构的外形控制和现场施工。

1 欧拉坐标找形法

1.1 计算假定

作出如下计算假定：

（1）忽略杆件抗弯刚度的影响，视作杆单元。

（2）单个杆件的自重均布荷载按照有限元基本理论等分到杆单元两端节点，形成等效节点力。

（3）每个杆件作为独立单元，截面面积保持不变。

1.2 基本原理

空间欧拉坐标系杆单元如图1所示。基于上述假设，结构的合理受力状态需要满足力学平衡的2个条件：①每个杆单元的横向、竖向长度与杆端力成比例，满足杆单元平衡；②每个节点各个方向的杆端力的代数和为零，即满足节点力平衡。

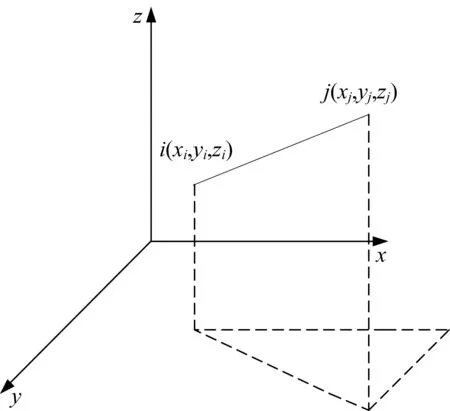
图1 空间杆单元示意图Fig.1 Schematic diagram of spatial rod element

在杆长和轴力已知的情况下，若要保持杆单元平衡，杆端力之间则必然符合一定的三角函数关系。此外，在迭代过程中若要满足正确的收敛趋势，则各力之间符号的相对关系是不变的。

该杆单元向量可表示为：

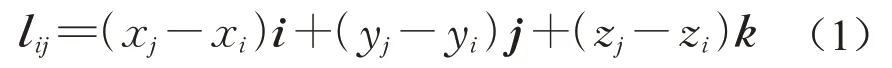
式中：lij为杆单元向量；i、j、k分别为3个方向的单位向量。

设定轴力符号与杆单元i端力的符号保持一致，以受拉为正。根据杆单元平衡可以得到力与坐标的关系式，如下所示：

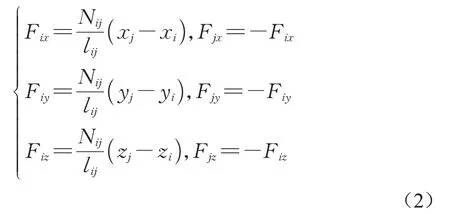
式中：Nij为轴力；lij为杆长度。通过整理可以得到以下杆单元平衡迭代方程：

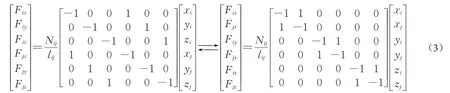
在杆长和轴力已知的情况下，可以直接建立单元杆端力与节点坐标的杆单元平衡迭代矩阵。令

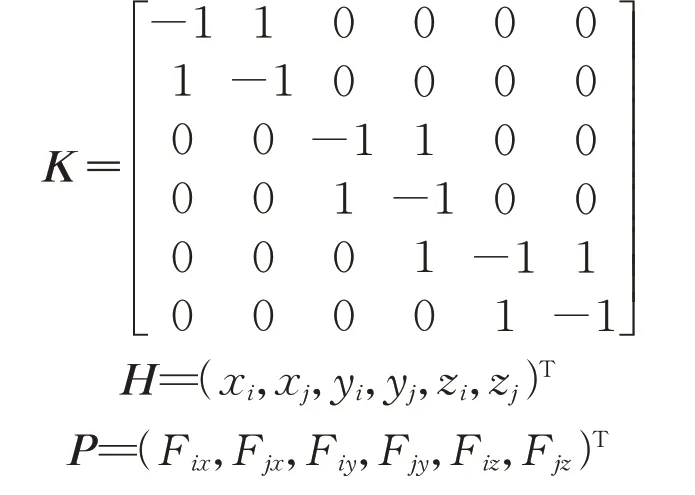
可得

式中：qij为力密度，定义为单位长度的轴力，即Nij/lij=qij。

1.3 杆件总长度最小状态方程

结构杆件的总长度是衡量成本的一项重要指标。在静力平衡状态下，结构内力与杆件长度达到比例平衡，通过控制两者的比例关系，理论上能达到结构杆件总长度最小的目标。可以发现，矩阵K与坐标向量H的乘积表示相邻节点之间在3个坐标轴上的投影距离。

设杆件的长度向量为l，则长度平方加权总和为

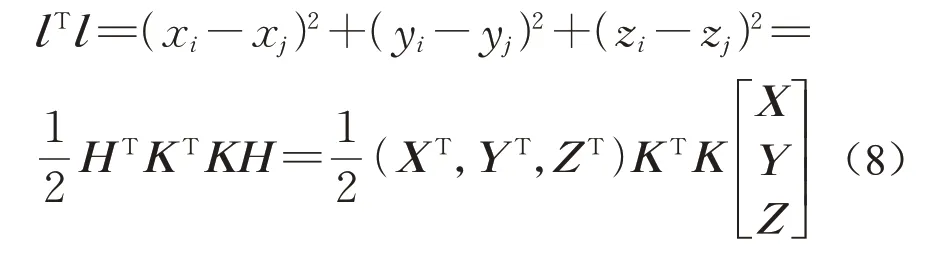
对称矩阵K由三部分组成，即Kx、Ky、Kz，如下所示：

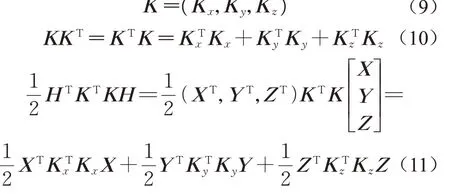
对于lTl取得最小值的问题，可以通过对x、y、z求导来解决，如下所示：

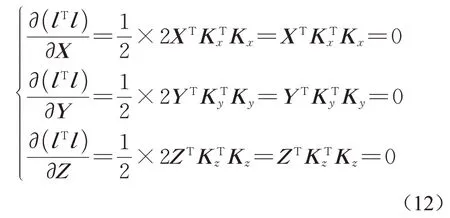
合并为

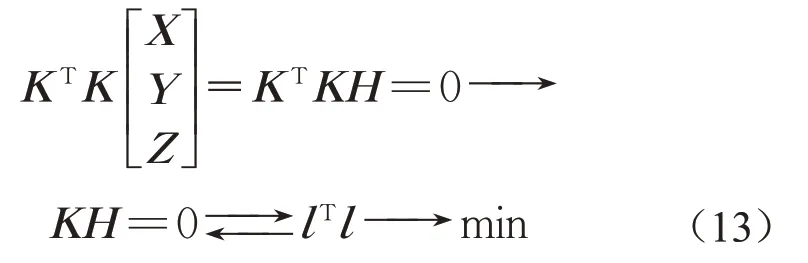
比较式（4）与式（13）可以发现，杆件最小长度的状态方程与平衡方程相似，只需将式（4）中qij=Nij/lij=1，并且荷载向量P=0，两式就完全等价，即：当结构荷载为零时，力密度取值为1，最小长度问题就可以使用欧拉坐标找形法的平衡方程来求解，此时得到的是杆件总平方长度最小的形状。由Schek［6］提出的力密度法推导得到的结论与此相同，说明了欧拉坐标找形法的真实性和有效性。

对于更一般的情况，可以将长度平方加权累加。设置特殊的权重gij=Nconst/lij，其中Nconst为结构杆件内力，可以通过以下计算式得到总长度最小的状态方程：

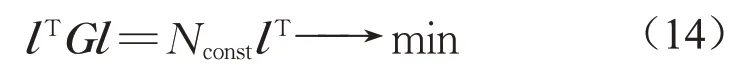
式中：G为权重向量，由各单元的权重组成。

1.4 迭代格式

①②2个杆单元总共3个节点，2号节点为共同节点。按照式（3），根据平衡条件与比例关系，建立格式相同的平衡方程。可以发现，2个杆单元可以依照组集规则，构建总体平衡迭代矩阵。为方便组集规则演示，可以表示为与其中q1表示①单元的力密度，q2表示②单元的力密度，k11、k12、k21、k22、k23、k32、k33为刚度矩阵元素。

以共节点为例，组集总体平衡迭代矩阵如下所示：

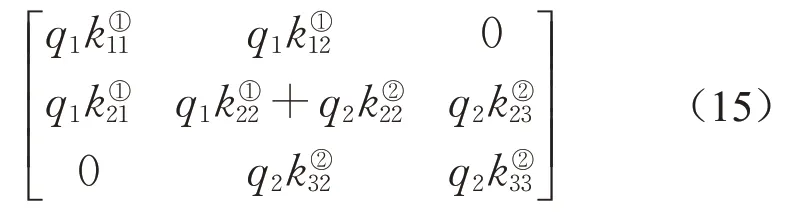
类似地，组集所有的节点单元平衡迭代矩阵可以形成总体平衡迭代矩阵Ktotal。迭代过程中，平衡迭代矩阵是关于上一阶段（第（n-1）阶段）杆件轴力和长度的函数，可以表示为Ktotal(Nn-1，ln-1)，其中Nn-1为第(n-1)阶段的轴力向量，ln-1为第(n-1)阶段的长度向量。依照组集规则，可以推导出第n阶段整个节点的总体平衡迭代方程式，如下所示：

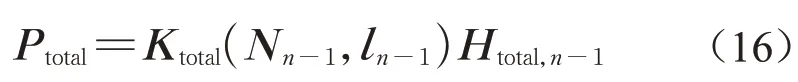
式中：Ptotal为结构的外荷载向量；Hn为第n阶段节点坐标向量。轴力向量的元素与长度向量的元素分别为

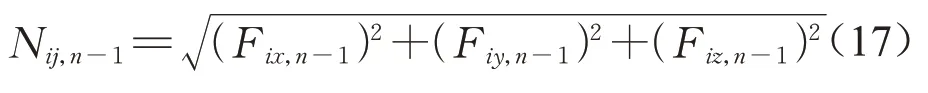
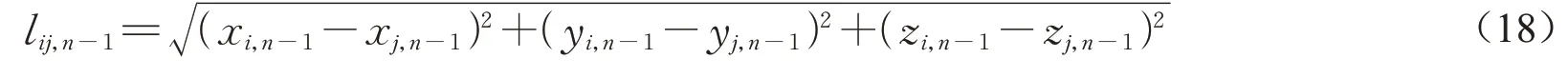
式（17）和式（18）中：Fix，n-1、Fiy，n-1、Fiz，n-1分别为第(n-1)阶段i端的杆端力；xi，n-1、yi，n-1、zi，n-1、xj，n-1、yj，n-1、zj，n-1分 别 为 第(n-1)阶 段i、j点 的 坐 标；lij，n-1、Nij，n-1分别表示迭代第(n-1)阶段所确定的单元杆长与轴力。

1.5 平衡方程的迭代求解条件

（1）初始参数的设定

欧拉坐标找形法初始参数设置可分为2种：①确定杆件恒定轴力向量N，在迭代过程中通过设置Nn=Nn-1ln/ln-1达到索网轴力均匀的目的；②根据经验调整杆件力密度，直接得到索网找形后的节点坐标。

（2）边界条件的处理

因为总体平衡方程的未知数是坐标，而不是有限元中的位移，所以在考虑边界条件时，对已知的节点坐标类似于强迫位移进行处理。采用主元充大数法，对于总体平衡迭代矩阵的第i个自由度点坐标Ui，原第i个平衡方程为

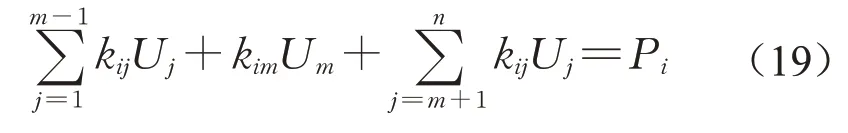
式中：m和n为刚度矩阵维度；Pi为荷载向量的元素。将矩阵对角元中充一大数D，并采取修改荷载项的方式进行处理，平衡方程变为

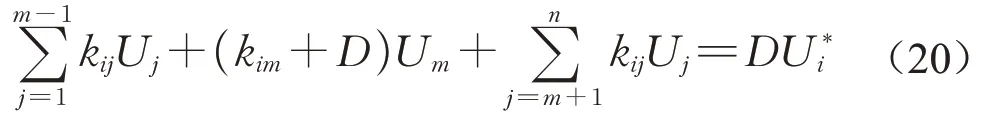
由于大数D数值很大，可得到Um≈U*i，从而将限制坐标体现在平衡迭代方程中。

（3）收敛条件的确定

第1种初始参数设置方法需要增加收敛条件，相较于上一迭代阶段的3个方向坐标差平方和epx小于10-6，计算式如下所示：

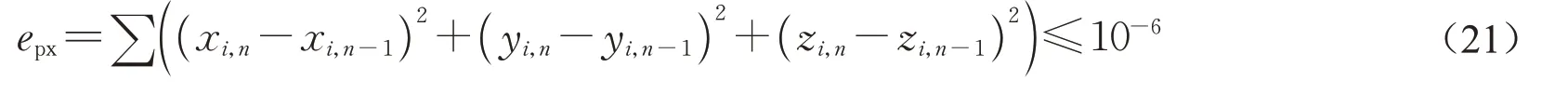
满足条件后，说明迭代过程中节点坐标不再发生变化。

1.6 欧拉坐标找形法的流程

欧拉坐标找形法的核心思想是在整体坐标系内，按照杆单元的力学特性直接建立节点坐标和杆端力的平衡迭代矩阵，将“坐标-杆端力”的平衡迭代矩阵比拟成传统“位移-杆端力”的有限元刚度矩阵。将坐标约束条件比拟成强迫位移条件，按照一定规则集合平衡迭代矩阵，从而建立总体平衡方程的迭代格式。依据前述原理利用Matlab软件编制求解程序，该程序的流程如图2所示。

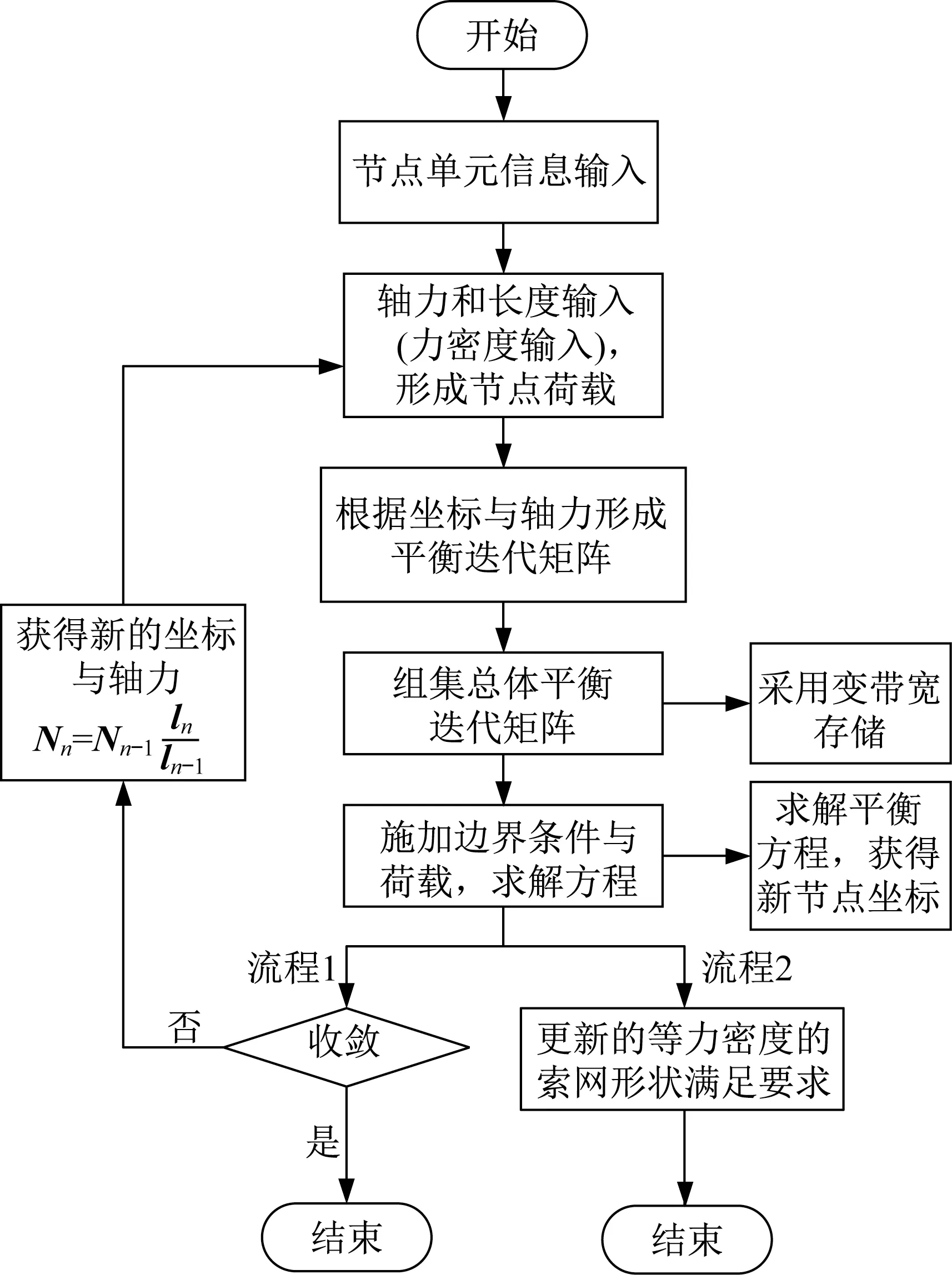
图2 欧拉坐标找形法流程Fig.2 Flow chart of Euler coordinates form-finding method

2 应用

欧拉坐标找形法是从杆件无弯矩的假定出发，将初始结构中的节点坐标与杆单元轴力作为初始参数，并建立迭代格式，从而求解出无弯矩状态下的最终结构形态。从力学角度来看，最终得到的结构形态是最为合理的一种受力形状。本节中主要对坐标迭代法进行验证，对边界条件、网格类型、初始参数等参数进行研究，以说明欧拉坐标找形法的适用性。

2.1 无荷载结构的最小长度状态找形

由第1.3节的推导可知，当外荷载为零、网壳的杆件力相同时，杆件总长度最小。在数学领域，普拉托提出过极小曲面的概念，是由肥皂泡引发的猜想，即利用一根铁丝，就会形成一个处于平衡状态的彩色薄膜。如果忽略混合液体自身的质量，也不考虑风力等外部干扰因素，薄膜的势能在表面张力的作用下就会达到最小值，而肥皂膜所呈现的曲面形状必然具有最小的面积。目前具有解析式的常见极小曲面有悬链线曲面、螺旋线曲面和Scherk曲面，利用本方法可以便捷地形成上述3种曲面。

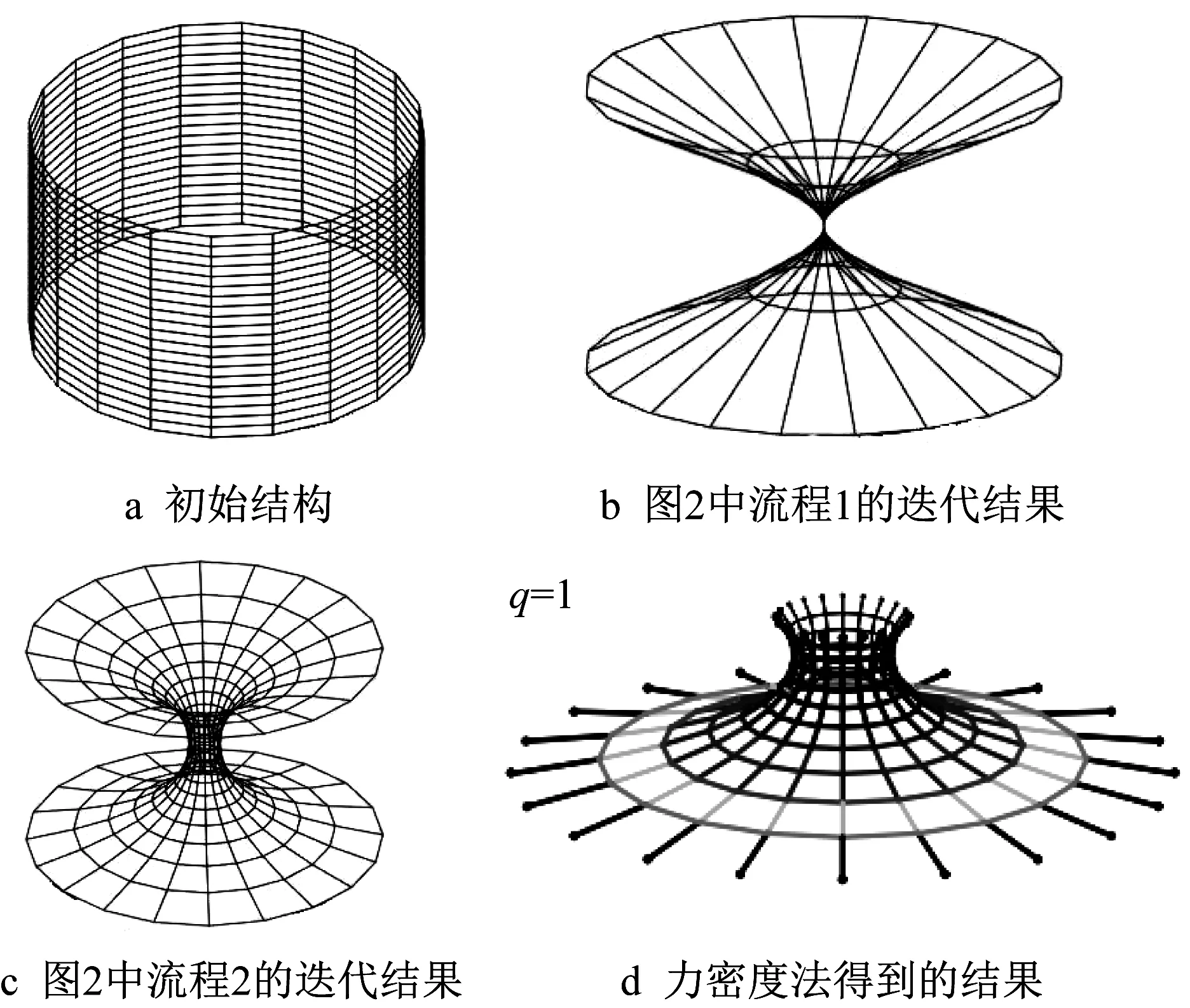
图3 悬链线曲面Fig.3 Catenary curved surface

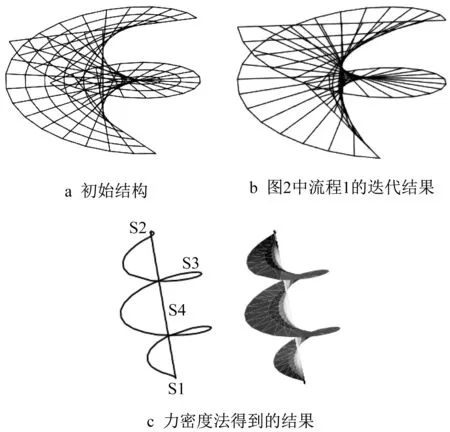
图4 螺旋线曲面Fig.4 Spiral surface

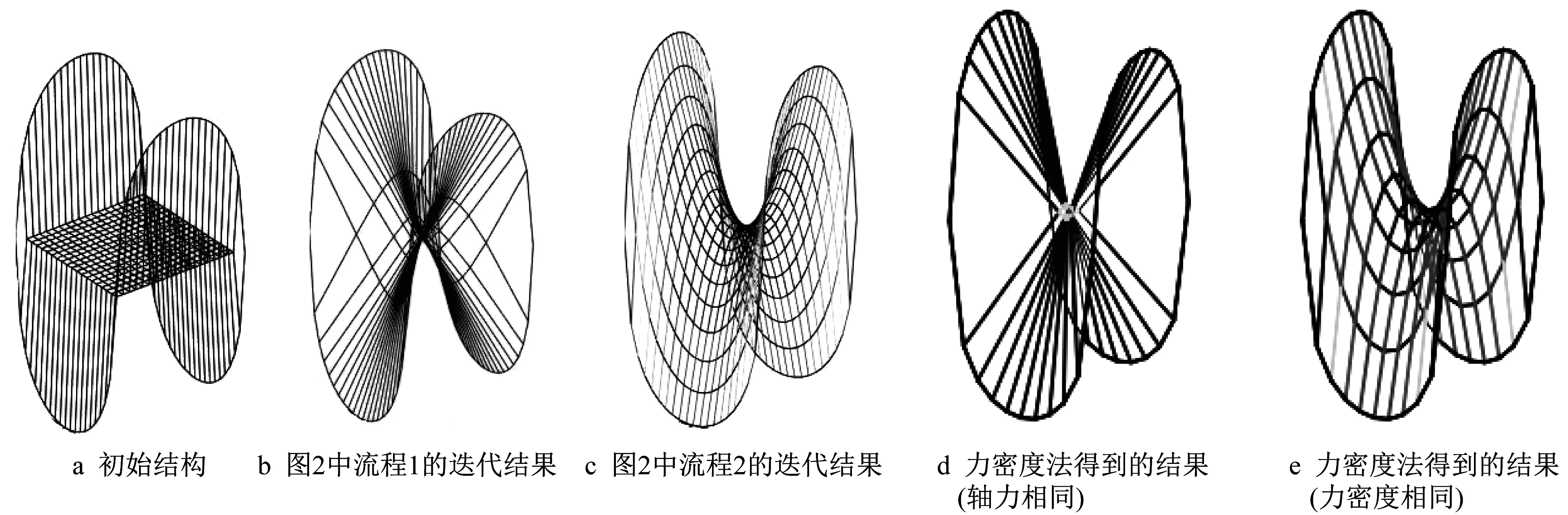
图5 Scherk曲面Fig.5 Scherk’s surface

2.2 双曲抛物面找形

为了进一步验证本方法的正确性和适用性，选取建筑设计中最为常见的双曲抛物面作为实例。双曲抛物面网格参数与迭代条件按照文献［22］设置，正方形平面边长为10，立面高度为5。初始网格如图6a所示，其平面投影如图6b直线规则部分所示。图2中流程1的迭代结果如图6c所示，所有杆件轴力为1，网格分布均匀，也验证了此类型网格适用于流程1。从图6b平面投影变化可以看出，网格向内收缩，对角线网格位置不变，其他网格向对角线偏移靠近，越远离边界的网格偏移的幅度越大。

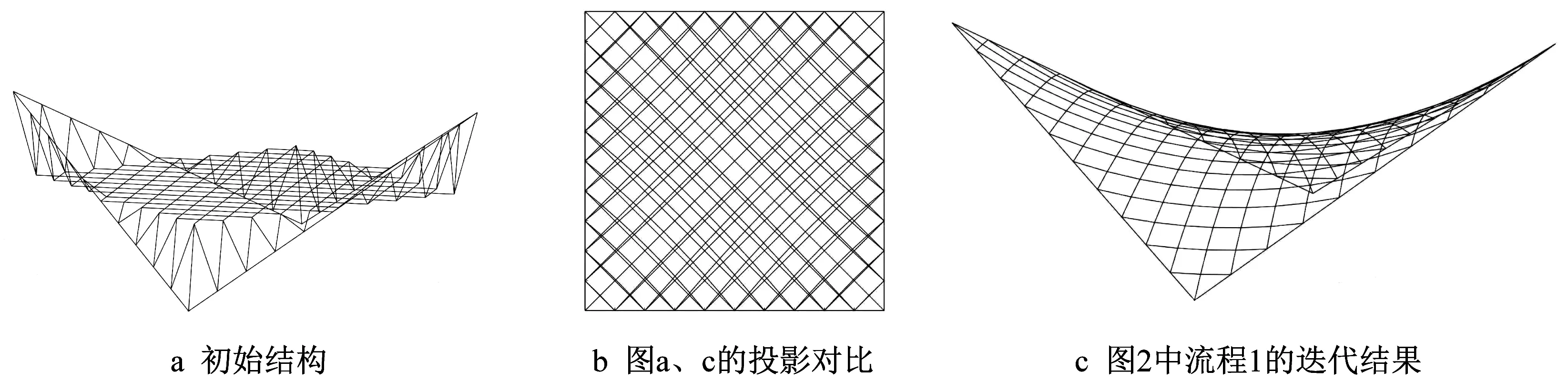
图6 双曲抛物面Fig.6 Hyperbolic paraboloids surface

2.3 马鞍形曲面找形

马鞍形曲面平面网格参数与双曲抛物面相同，正方形平面边长为10，初始网格如图7a所示。边界条件为两边半径5的圆弧，另外两边固定。图2中流程1的迭代结果如图7b所示，所有杆件轴力为1，马鞍形曲面特征明显。由如图7c所示的平面投影变化可以看出，网格呈现对称分布，网格均匀。对角线网格为适应马鞍形曲面的特征，其位置发生变化，网格向两固定边收缩。

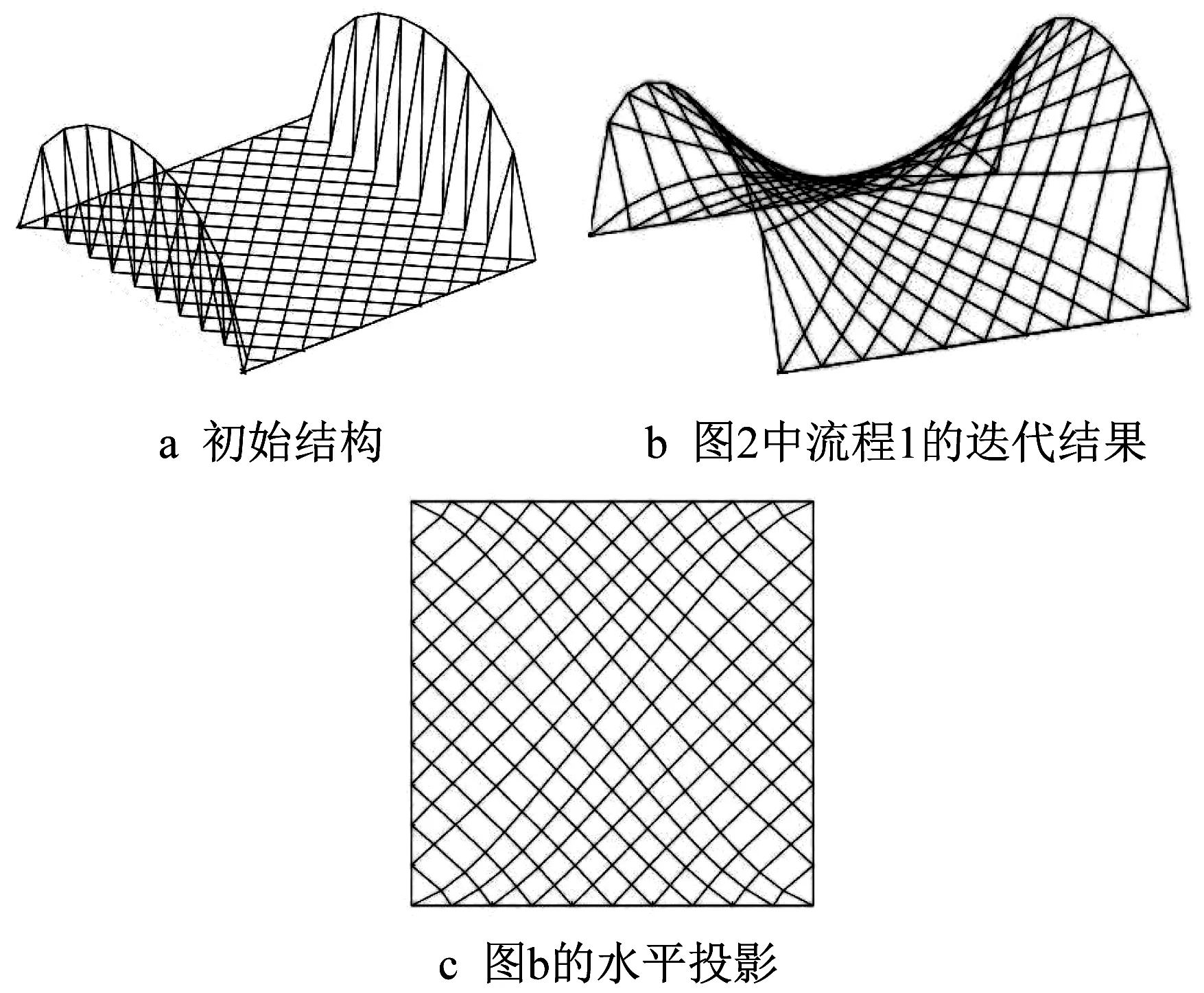
图7 马鞍形曲面Fig.7 Saddle-shaped surface

2.4 边界条件的影响

从双曲抛物面和马鞍形曲面的实例可以看出，相同的网格划分会因为不同的边界条件而产生不同的优化结果。为了进一步探究边界条件对于算法找形结果的影响，选取与马鞍形曲面相同的平面网格，将圆弧边界保留，释放另外两边的约束。图2中流程1的迭代结果如图8a所示，所有杆件力为1。由如图8b所示的平面投影可以看出，释放边界约束后，网格向中间猛烈收缩，导致中间网格密度较大，同时受约束的边界网格则分布较为均匀。从极小曲面实例也可以看出，边界约束会影响周围网格的长度和分布均匀程度。

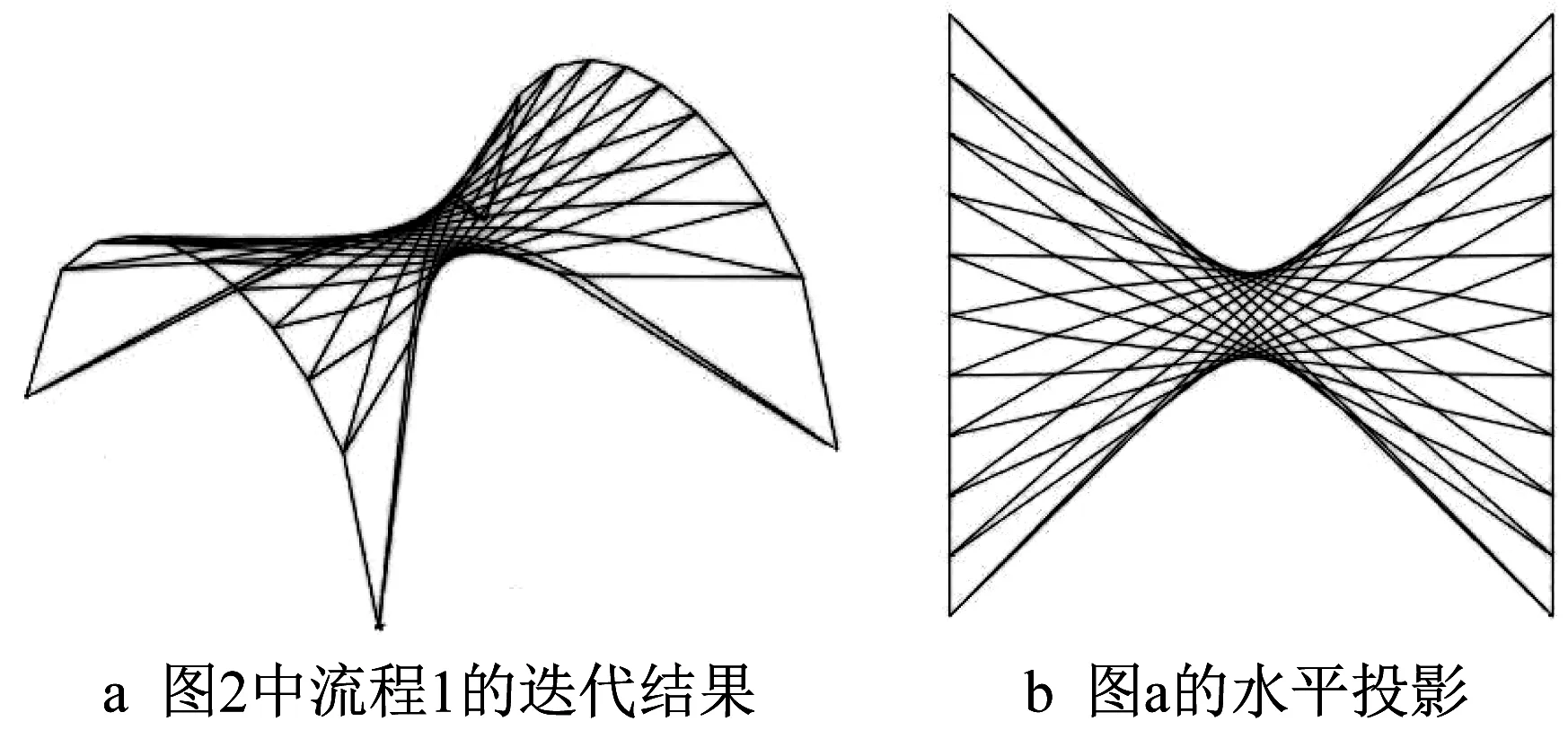
图8 四点固定的马鞍形曲面Fig.8 Four-point fixed saddle-shaped surface

欧拉坐标找形法可以在边界条件中指定三维坐标的数值，而力密度法只能限制固定点，因此欧拉坐标找形法具有很大的优势。选择了如图6所示的双曲抛物面，边界和网格划分条件保持不变，限制平面坐标，从而实现投影网格在优化过程中不变的目标。图2中流程1的迭代结果如图9所示，三维形状变化不大，并且平面投影网格更加均匀，这说明了本方法控制坐标的优越性。

2.5 网格划分的影响

选取螺旋线曲面，采用三角形网格划分，其余参数和图4a的参数相同，结果如图10a所示。图2中流程1的迭代结果如图10b所示，杆件力均相同。图10b与图4b相同，因此网格划分对于找形结果无明显影响。

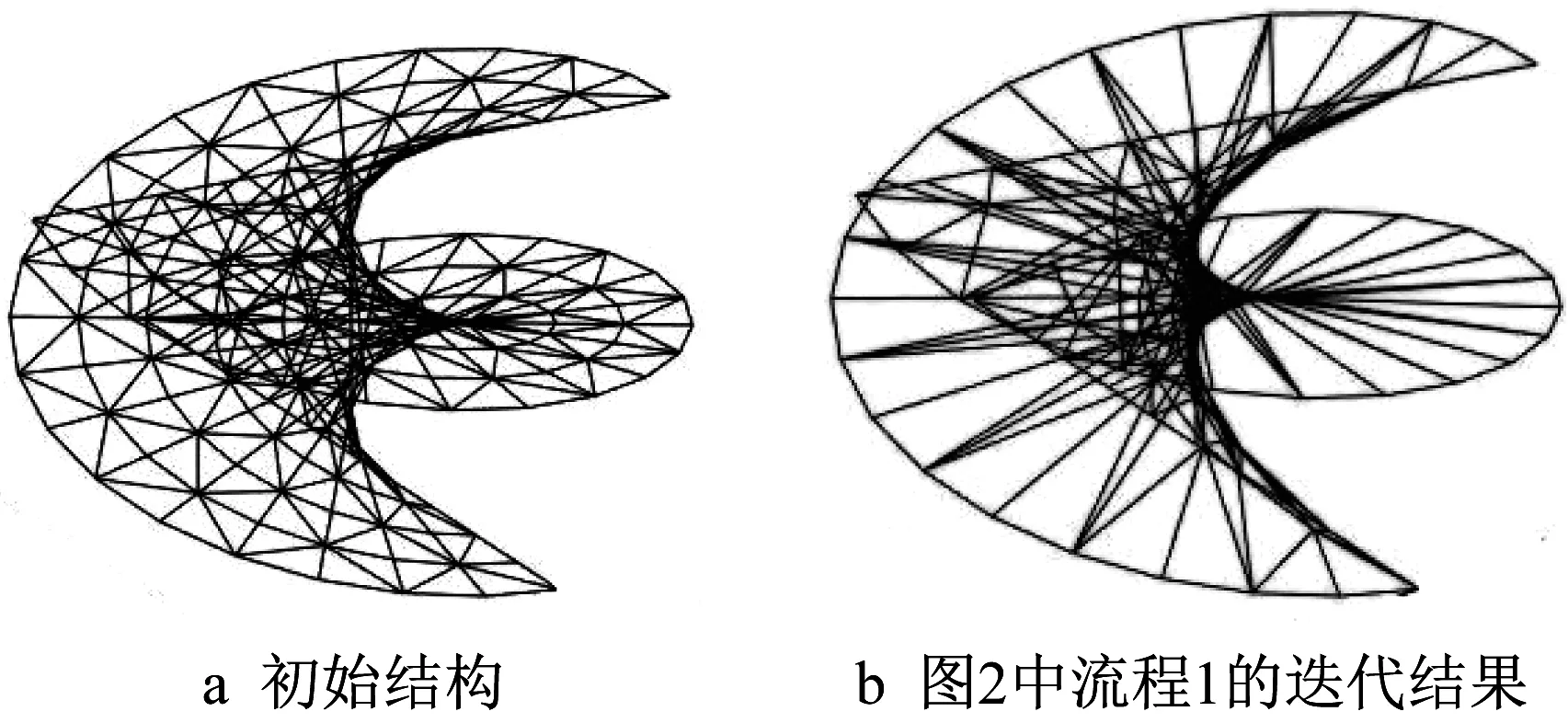
图10 三角形网格的螺旋线曲面Fig.10 Spiral surface with triangle mesh

3 结论

（1）理论和实例都验证了在无荷载条件下，最终形状能够满足总长度最小或者总长度平方和最小。

（2）本方法相较于传统力密度法，可以方便地改变边界，控制节点三维坐标，并且迭代格式简单，适应性较强，收敛稳定。

（3）边界条件对最终的找形结果影响较大。相同的初始条件，改变边界条件会产生完全不同的找形结果。同时，内力一致或力密度一致时，边界处节点坐标相较于初始状态变化较小，远离边界处节点坐标变化较大，而且杆件长度更小。网格划分的方式不同（如四边形网格和三角形网格）基本不会影响最终的找形结果。

作者贡献声明：

刘超：提出算法，指导算法推导。

詹海鹏：算法的编程和算例的计算，论文撰写。