深度神经网络在高铁运行环境识别中的鲁棒性验证
高 珍,苏 宇,侯潇雪,方 沛,张苗苗
(同济大学软件学院,上海 201804)
人工智能(artificial intelligence,AI)[1]是当今的热门话题之一,机器学习[2]、神经网络等人工智能技术近年来得到广泛应用。然而,人工智能的广泛应用也带来了一些安全风险和隐患,包括人工智能系统的错误、网络攻击和鲁棒性等问题[3-4]。研究人员发现,包括神经网络在内的大多数机器学习模型的鲁棒性都很差,这限制了其在安全性至关重要领域的应用[5]。
目前神经网络处理效果评估主要依靠神经网络在测试集上的精度,然而测试集的数据与训练集、验证集的数据往往属于独立同分布,即测试集中并不包含被干扰过的图像,这使得大部分在测试集上表现良好的神经网络模型在面对异常样本时表现很差。将这些异常样本加入测试集重新训练神经网络来提高其鲁棒性是一个可行的办法,但是类型多变的异常样本导致新的异常样本不断产生,将新的异常样本不断加入测试集,从而引起测试准确度的不稳定,因此研究人员更多地考虑验证而非测试的方法来评估神经网络的鲁棒性[6]。
系统安全性验证通常采用基于严格的数学模型的形式化方法[7-8]。目前,一些验证技术如模型检验、定理证明等在嵌入式系统中已经有了非常成熟的应用[8],文献[9-15]中给出了基于形式化方法的神经网络验证技术,也由此提出了神经网络验证工具,如Reluplex[9]、DLV[12]、SafeCV[13]、DeepTRE[16]等。
2019年,Ruan等[16]将神经网络的全局鲁棒性定义为测试集上的最大安全半径期望,并迭代计算其上下界序列。实验结果表明,神经网络鲁棒性的上下界序列会逐渐收敛为同一值,即全局鲁棒性的近似值,将这种基于L0范数的神经网络鲁棒性量化方法命名为DeepTRE(tensor-based robustness evaluation for deep neural network)。DeepTRE平衡了计算效率和对抗样本的效果,在标准数据集如MNIST和CIFAR上具有良好的验证结果。
以高铁运行环境识别网络为背景,采用DeepTRE验证网络的鲁棒性。在使用DeepTRE验证网络的过程中,由于内存不足而导致验证中断,因此对DeepTRE实现进行了一些改进,包括由局部鲁棒性计算改为全局鲁棒性计算、允许任意设置扰动值、设定验证范围、多轮预测以减少空间复杂度4个方面。最后,基于改进的DeepTRE对识别任务进行验证实验,并与其他神经网络验证工具DLV和SafeCV进行对比。
1 DeepTRE实现的改进
1.1 DeepTRE基本概念
给定一个用于m分类的神经网络f∶Rn→Rm,对于一个输入x∈Rn,输出f(x)=(c1(x),…,cm(x))∈Rm,其中ci(x)表示第i个标签的置信度。不失一般性,将输入x归一化为[0,1]n,输出f(x)使用Softmax层归一化为[0,1]m。用表示输入为x时对应的输出的分类标签。
定义1(全局鲁棒性)给定神经网络f一个有限的 原 始 输 入 集T0和 距 离 范 数‖·‖D,对 于 所 有i∈{1,…,|T0|}原始输入集T0=(x0,i)i=1,…,|T0|,原始输入集T0中的图像在添加扰动后得到对抗样本数据 集T=(xi)i=1,…,|T0|。全 局 鲁 棒性R(f,T0,‖·‖D)计算是一个优化问题,即计算T0与T之间的最小距离,如下所示:
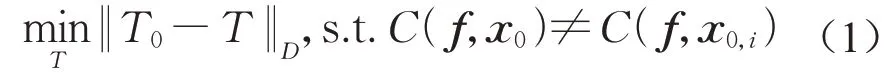
DeepTRE中使用距离范数L0衡量图像之间的距离,并定义输入图像数据集之间的距离是数据集中所有相应图像之间距离的期望,计算式如下所示:

定义2(子空间完备集)给定一个输入x0∈[0,1]n和一组维度为t的正整数集合T⊆{1,…,n},|T|=t,t≤n。定义x0的子空间Xx0,T为一组输入x∈[0,1]n的集 合,对 于 任 意i∈T有x(i)∈[0,1],对 于i∈{1,…,n}T有x(i)=x0(i)。输入x0的子空间完备集为X(x0,t)={Xx0,T|T⊆{1,…,n},|T|=t}。
Xx0,T中的每个元素与x0相比除T中指定的像素外的值都相等,即子空间Xx0,T中的每个元素都是x0改变了T中指定的像素、其他的像素保持不变之后得到的图像。由于在t维的情况下T有多种组合,因此X(x0,t)是在所有可能的T下Xx0,T的集合。
定义3(子空间敏感度)给定输入子空间X⊆[0,1]n,输入x0∈[0,1]n,输出标签j,关于X、x0、j的子空间定义如下所示:

引入测试集T0和维度t后,子空间敏感度定义如下所示:

神经网络f对输入x0的输出分类标签记为jx0=C(f,x0)。直观上来看,S(X,x0,j)表示集合X中所有修改后的图像与原图像x0相比分到j类别置信度的最大下降值,S(T0,t)表示X(x0,t)所有的子空间和T0中所有输入的分类标签置信度的最大下降值的二维数组。
式(4)的时间复杂度是一个难点问题。当给定测试集T0和维度t时,计算S(T0,t)中所有元素的时间复杂度O(|T0|nt),S(T0,t)中每项元素的表达式都可以看作一个优化问题。以MNIST(Mixed National Institute of Standards and Technology database)数据集为例,每张图片的像素大小为28×28,假设测试集T0中有20张图像,在维度t=1的情况下复杂度为28×28×20=15 680,即15 680个一维优化问题。DeepTRE通过GPU并行化来解决该问题,解决思路为将式(4)中的非线性、非凸优化问题转换为张量公式。
1.2 DeepTRE介绍
DeepTRE主要包含敏感度矩阵计算和鲁棒性上下界计算两部分。一般来说,在攻击方法中生成对抗样本时计算得到的最小扰动是鲁棒性的上界,而保证一定不会产生对抗样本的最小扰动是鲁棒性的下界[17]。DeepTRE使用L0范数(即对抗样本与原图像相比改变像素的个数)衡量对抗样本和原图像之间的距离。要得到神经网络全局鲁棒性的上下界,就要对测试集中每个图像x计算子空间敏感度矩阵S(T0,t)。
假设输入数据集中图像像素大小为w×h(w为图像宽度,h为图像高度)、类别数量为m,对每个像素添加扰动的次数为p。对扰动后得到的张量进行模1展开(mode-1 unfolding),得到的矩阵由w×h×p个元组组成,每个元组包含2个子元组,一个是第i次只改变t个像素后的图像,i∈{1,…,p},即子空间完备集,另一个是原图像和扰动后图像在Softmax层输入中的m个类别差值。将得到的矩阵按第2个子元组原始类别的差值从大到小排序,即按照相应像素改变对正确类别影响从大到小排序,得到敏感度矩阵S(T0,t)。敏感度矩阵实际表示的物理意义是同时改变t个像素的组合对神经网络输出正确类别概率的影响。
对于鲁棒性下界的计算,只需要检测张量S(T0,t)第3维第1行的图像是否会发生类别变化,即检测S(T0,t)[∶,∶,1]∈Rn×p是否有C(f,S(T0,t)[∶,∶,1])≠C(f,T0)。如果没有,鲁棒性下界就是t,反之说明改动t个像素足以引起图像类别发生改变,那么此时鲁棒性下界就是t-1。
对于上界的计算比较复杂,包含了累加和剔除2个部分。在累加部分,对于T0中的每个输入图像,根据敏感度矩阵从上到下的顺序,从原图像开始迭代,采用敏感度矩阵中的扰动,直到图像类别发生变化,此时生成的图像一定是一张对抗样本。剔除部分是在这张对抗样本基础上进行的,每次恢复敏感度矩阵中一行的t个像素的值,如果剔除了这t个像素后的对抗样本仍然分类错误,就说明这t个像素不会对分类结果产生影响,这t个像素仍然保持恢复后的原值,否则撤销这一步的剔除。如此,将敏感度矩阵中的w×h×p个元组剔除一次后得到的更改像素个数就是鲁棒性的上界。
1.3 DeepTRE的不足
首先,Ruan等[16]在对DeepTRE的介绍中提出了全局鲁棒性的概念,在案例3的实现中,虽然验证时载入了测试集中的所有图像,但是在每张图像上的鲁棒性分析是独立的,得出的结论也是神经网络在每张图像上的局部鲁棒性。因此,扩展案例3,使其支持全局鲁棒性。
其次,DeepTRE在进行鲁棒性评估时,并没有设定验证范围,这不符合实际情况。根据对抗样本的定义,生成的对抗样本与原始图像之间的距离需要限制在一定范围内,这个距离限制保证了对抗样本与原始图像的相似性,将这个范围称为验证范围,即在验证范围内用人眼看对抗样本与原始图像应该属于同一类别,超过验证范围后人眼可轻易区分对抗样本与原始图像,不会将两者划分到同一类别。DeepTRE只强调找到一个扰动的上界,当扰动超过上界时一定能够找到对抗样本。然而,当上界超过验证范围时,该上界值也就没有了意义,因此引入验证范围的概念。
最后,分析原始算法的空间复杂度。假设测试集中共有λ张图像属于m个类别,每个像素的扰动次数为p,每张图像的像素大小为w×h×γ,其中γ为图像通道数。DeepTRE在算法实现中有3个较大的矩阵:第1个矩阵是存储测试集图像地址的矩阵,由于DeepTRE将测试集中所有图像的地址存储在一个矩阵中,并依次在每张图像上计算神经网络的局部鲁棒性,因此矩阵的空间度复杂度为O(λ);第2个矩阵是输入给神经网络的张量,由w×h×p个元组组成,每个元组保存添加扰动后图像的像素值,大小为w×h×γ,对每个被保存的扰动后图像,有(w×h-1)个像素的值与原图像相同,一个像素的值因添加扰动而不同,每个像素被添加p次扰动,因此矩阵的空间复杂度为O(w×h×p×w×h×γ);第3个矩阵是神经网络输出的敏感度矩阵,由w×h×p个元组组成,每个元组保存Softmax层在m个类别的输出,矩阵的空间复杂度为O(w×h×p×m)。因此,总空间复杂度为O(λ)+O(w×h×p×w×h×γ)+O(w×h×p×m)。一般而言,测试集中图像数量和类别数量不会过大,因此算法的总空间复杂度为O(w×h×p×w×h×γ)。以ImageNet数据集为例,每张图像的像素大小为224×224×3,默认扰动次数p=2,空间复杂度为224×224×2×224×224×3=15 105 785 856。可以看出,当数据集规模变大时,算法的空间复杂度急剧增加,使得验证无法进行。
1.4 DeepTRE的改进
基于上述原因,对DeepTRE进行改进,使其支持大规模图像验证,具体的改进内容包括由局部鲁棒性计算改为全局鲁棒性计算、允许任意设置扰动值、设定验证范围、多轮预测以减少空间复杂度4个方面,接下来对改进过程进行详细介绍。
使用变量Lv表示验证范围。由于DeepTRE是基于L0距离,因此Lv直观上表示的是改变的最大像素数。当改变像素的个数小于Lv的下界时,认为生成的对抗样本与原样本应该属于同一个类别;当改变像素的个数大于Lv的上界时,认为添加的扰动过大,用人眼看来生成的样本与原样本类别不同。改进后的DeepTRE算法如图1所示。

图1 改进后的DeepTRE算法Fig.1 Improved DeepTRE algorithm
图1是改进后的DeepTRE算法,使用GetFeatureMap、Accumulate和Refine 3个函数分别表示敏感度特征图计算、像素扰动累积和像素变化恢复3个子过程(后续介绍3个函数)。图1中,φ表示排序后的特征图,g表示是否找到对抗样本的布尔值,n和α表示整数变量,x表示测试集取到的单张图片,x~表示像素扰动产生的样本,x′表示剔除对类别变化无影响的像素后得到对抗样本。g=true表示像素扰动累积过程中在验证范围内发现了一个对抗样本,然后对此对抗样本进行像素变化恢复,并计算其扰动上限。相反,g=false表示在像素扰动累积过程中即使对所有像素都添加了扰动也不足以引起图像类别的变化,说明神经网络模型在这张图像上的鲁棒性强,可将所有g=false的图像x保存到S中输出。在剔除对类别变化无影响的像素后得到对抗样本,用函数d度量原始图像x与对抗样本x′之间的距离,如果该距离大于验证范围,就认为对抗样本x′不是真正的对抗样本,同时将原始图像x保存到S中输出。
敏感度特征图计算算法GetFeatureMap如图2所示,其中y表示神经网络模型对图片x的分类标签,x~是对x的复制,方便尝试扰动。对于测试数据集中每个带有标签的图像x,按照像素位置的顺序一次改变一个像素值,其余像素值不变。计算所有扰动后的图像x~在f的Softmax函数中的输入矩阵,依次记录每个矩阵在y标签下的值并按升序排序,得到每张图像排序后的特征图,即敏感度特征。图2中,s^(β)是检索模型Softmax层的输入,sort(M,t)是按给定维度t对矩阵M进行排序。用户可以任意设置扰动的大小δ,从而代替原算法中的每个像素的扰动次数p。由于图像像素值被归一化至0到1之间,因此像素最大值为1,当添加扰动后的像素值超过1时设置该像素值为1。新的敏感度矩阵计算算法大大减小了空间复杂度。在原算法中将所有添加扰动后的图像放入同一个张量,随后将张量输入神经网络进行预测,因此神经网络的输入以及预测后输出的矩阵都非常大。在改进后的算法中,采用多轮输入神经网络预测的方法,每生成一批扰动后的图像就输入神经网络进行预测,以时间换空间,大大减小了对内存的需求。

图2 子空间敏感度计算方法Fig.2 Subspace sensitivity calculation algorithm
改进后的Accumulate算法伪代码如图3所示。依次在原始图像x上累加敏感度矩阵φ中的扰动,并将所有扰动后的图像保存在矩阵M中。将矩阵M输入到神经网络,预测得到标签矩阵Y^,如果Y^中存在标签与图像原始标签y不同,就说明M中存在对抗样本。M中图像的扰动数量依次增加,第1张图像M[0]即为改动像素个数最少的图像x~,返回g=true和找到的对抗样本x~。反之,如果对抗样本不存在,累加算法返回g=false和原始图像x。

图3 改进后的Accumulate算法Fig.3 Improved Accumulate algorithm
根据敏感度特征图计算算法,敏感度矩阵中的扰动次数为w×h,即对原始图像中的每个像素都扰动一次。若累加过程中对所有扰动都进行尝试,算法的空间复杂度则高达O(w×h×w×h×γ)。原累加过程增加了叠加扰动的范围k以限制累加扰动的数量。用户可以自由设置k的值,如果扰动像素数超过k,累加就终止,所以原累加算法的空间复杂度为O(k×w×h×γ)。当k设置过小时,原算法可能忽略存在的对抗样本;当k设置过大时,原算法的空间复杂度仍然很大。
在新的Accumulate算法中取消范围限制,规定每当矩阵M中累加的扰动数量为图像的宽w时,检测一次是否找到对抗样本,如果找到就返回g=true及找到的对抗样本,否则清空矩阵M中的值并在之前扰动后的图像基础上继续添加扰动。改进后Accumulate算法空间复杂度为O(w×w×h×γ)。
改进后DeepTRE的空间复杂度主要取决于新的敏感度矩阵计算算法,与原敏感度矩阵计算算法相比,改进后算法包含2个较大的矩阵,第1个为神经网络输入矩阵,第2个为Softmax层的输出矩阵。
对于第1个矩阵,假设测试集中共有λ张图像属于m个类别,用扰动δ代替原算法中的扰动次数p,这样可以在验证开始前任意设置扰动大小,而不需要在扰动时动态计算。每张图像的像素大小为w×h×γ。对扰动后的图像分e批处理,每批都有(w×h)/e个图像,因此输入给神经网络的张量大小为((w×h)/e)×(w×h×γ)。为方便实现,对于大型图像数据集,可以设置e=h。时间换空间的策略能有效降低空间复杂度,达到两者的平衡,此时空间复杂度为O(w×w×h×γ)。
对于第2个矩阵,不像原方法将m个类别在Softmax层的输出全部保存,由于只关注是否生成对抗样本,而不关注生成对抗样本的具体类别,因此对于原始图像xi生成的扰动后图像,只需保存第C(f,xi)类别Softmax层的输出即可,这部分的空间复杂度为O(((w×h)/e)×1)=O(w×1)。
因此,通过多轮预测优化,改进后DeepTRE的空间复杂度为O(w×w×h×γ)。
2 鲁棒性验证实验
对于DeepTRE,目前有严格的理论证明过程,但该方法只应用于少数公共数据集。在本节中,基于文献[18]中研究结果,使用改进的DeepTRE验证神经网络在高铁运营环境识别任务模型中[18]的鲁棒性。数据集大小为(30 000×224×224×3),即数据集包含30 000张RGB(red green blue),宽高为224×224。该数据集包含6个类别(类别0~5),分别是“白天有雾”、“白天晴天”、“白天有雨”、“夜间晴天”、“夜间有雨”和“隧道内”。数据来源为中国济南和重庆高铁运营期间的监控视频,涵盖了多种地形、拍摄角度、车辆类型、时间段、路段和天气情况。
2.1 使用改进的DeepTRE对高铁运营环境识别模型进行验证
实验是在使用Tesla K40c的GPU上进行的,验证范围Lv=50 000,扰动δ=0.5。采用包括6 000张图片的测试集对模型进行鲁棒性评估,改进后的DeepTRE对每张图像的平均搜索时间为10 min。实验后一共生成了1 792个对抗样本,每个类别分别有199、98、0、532、411、552个,攻击成功率为0.298 7。图4为改进后DeepTRE攻击各个类别生成的对抗样本示例,相应的对抗样本类别变化如表1所示。

表1 对抗样本的类别变化Tab.1 Category change of adversarial examples

图4 改进后DeepTRE生成的对抗样本示例Fig.4 Adversarial examples generated by improved DeepTRE
实验结果表明,改进后DeepTRE的攻击效果良好。直观上看,攻击“白天有雨”类别的效果不好,没有生成一张对抗样本,在其余5个类别中攻击效果均较好,在“夜间晴天”类别生成的对抗样本数量最多,与原样本的距离也最小。对于第7组和第9组图像而言,DeepTRE添加的扰动肉眼几乎不可分辨。对于“白天晴天”而言,部分图像添加的扰动个数很少(第7组),部分图像添加扰动个数却很多(第6组),但扰动像素个数与图像类别没有确定的关系。
已知DeepTRE全局鲁棒性上界是测试集上所有对抗样本与原图像之间距离的期望,为1 037 572/1 792=579(数据集中的扰动像素总数为1 037 572,有1 792个对抗样本)。通过实验给出了训练好的模型的鲁棒性上界为579。
在空间复杂度方面,改进前的DeepTRE由于空间复杂度过高导致显存溢出而无法进行实验,因此在理论上讨论改进前后DeepTRE空间复杂度的差异。为了减少复杂度,只考虑t=1维的情况。数据集中每张图像的像素大小为224×224,一共6个类别,在添加扰动得到敏感度矩阵后分224次输入到神经网络中进行预测,那么算法的复杂度为224×224×224×3=33 718 272。原DeepTRE空间复杂度为224×224×2×224×224×3=15 105 785 856,是改进后DeepTRE的448倍,改进后的DeepTRE以时间换空间的方法减少了中间矩阵的大小,使得能够支持更大图像像素和数量的数据集。
2.2 对比实验
采用2种神经网络验证方法DLV(deep learning verification)和SafeCV(safe computer vision)在同一识别案例中进行实验,并将验证结果与改进后DeepTRE进行对比。DLV通过离散化处理输入层或隐藏层的向量空间,然后在离散化空间上应用穷举搜索算法寻找对抗样本,从而验证神经网络的鲁棒性。SafeCV将对抗样本的搜索过程转化为双人回合制随机博弈,并通过蒙特卡罗树搜索逐步搜索博弈状态空间来寻找对抗样本。
DLV在使用过程中有2个问题。第一,DLV确保找到对抗样本是基于离散化方式对验证范围进行了穷举搜索,但增加了算法的时间复杂度;第二,将神经网络模型集成到DLV上时,需要给定的用户参数个数多达15个,因此影响对抗样本的寻找速度及寻找结果。对于第2个问题,采取多次实验的方法,尝试采用不同的参数值以丰富对抗样本的寻找结果。最终得到的重要参数值(节选)如下:numOfFeatures=10 000(表示验证网络每一层时考虑的特征数量),featureDims=5(每个像素的维度数量),controlledSearc=("L1",40)(使用L1范数度量扰动,扰动的L1范数小于40)。
相比之下,改进后的DeepTRE涉及的参数只有2个,对用户十分友好,同时验证速度也快于DLV。SafeCV的验证更快,远远快于DLV,略快于改进后的DeepTRE。
针对改进后的DeepTRE,DLV和SafeCV的实验结果中挑选6组进行对比,如图5所示。值得注意的是,改进后的DeepTRE并没有在“白天有雨”类别中找到一个对抗性例子。从视觉上可以直观地发现,3种方法在给定的验证范围内鲁棒性都未通过,DLV和SafeCV都需要对原图像改动很大才能攻击成功,除“白天有雨”类别外,改进后DeepTRE的改动明显少于其他2种验证方法。另外,虽然3种方法都是基于L0范数进行攻击的,但是攻击方式有较大的不同。DeepTRE是根据自身设计的像素敏感度计算方法进行搜索,而DLV和SafeCV是根据SIFT(scale invariant feature transform)计算像素响度提取特征进行攻击,同时SafeCV增加了蒙特卡罗树搜索,以双玩家博弈的方式计算出最优解。

图5 原始图像和改进后DeepTRE、DLV、SafeCV生成的对抗样本Fig.5 Original images and adversarial examples generated by improved DeepTRE,DLV and SafeCV
表2为6组图像对应的类别变更。表2中,N表示在给定验证范围内未找到对抗样本。从定量角度看,DLV和SafeCV改动的像素个数大部分都在万级别,而改进后DeepTRE改动的像素个数大部分在几百左右。

表2 由改进后的DeepTRE、SafeCV和DLV攻击产生的对抗样本的类别变化Tab.2 Category change of adversarial samples generated by improved DeepTRE,SafeCV and DLV
在维度t=1的情况下,改进后的DeepTRE得到基于L0的神经网络全局鲁棒性下界为1,上界为579,而DLV和SafeCV都是针对单个输入图像,如果在一定范围内能够找到对抗样本,神经网络就是不鲁棒的,如果没有对抗样本,神经网络就是鲁棒的,并没有给出全局的证明。DLV在L1小于40的区域内针对所有输入图像都找到了对抗样本,因此DLV得到基于L1的鲁棒性上界小于40,基于L0的鲁棒性上界小于(numOfFeatures×featureDims)10 000×5=50 000;SafeCV的运行速度很快,采用蒙特卡罗树搜索返回最优结果,尽管得到了最优结果,但是除“夜间晴天”类别中的个别输入图像外,大部分图像改动的像素个数都是上万,从视觉上认为生成的对抗样本改动过大,甚至人眼都可以将对抗样本与原始图像区分,因此SafeCV方法在模型和数据集上的验证效果较差,得出的鲁棒性上界也过大。
在验证效果方面,改进后的DeepTRE要显著强于DLV和SafeCV,可以在更小的L0下生成对抗样本。从运行时间上看,改进后的DeepTRE明显快于DLV,但是略慢于SafeCV。
3 结语
通过对DeepTRE进行优化降低了DeepTRE的空间复杂度以支持大规模图像数据集,改进内容包括由局部鲁棒性计算改为全局鲁棒性计算、允许自定义设置扰动值、设定验证范围、多轮预测以减少空间复杂度4个方面。最后,采用实验验证了改进后的DeepTRE的效果。结果表明,一方面改进后的DeepTRE显著降低了空间复杂度以支持更大规模的数据集,另一方面改进后的DeepTRE相较于DLV和SafeCV在较快的验证速度下拥有更优异的验证效果。
作者贡献声明:
高珍:论文审阅与修改,算法设计指导。
苏宇:模型构建,算法设计与实现,论文撰写。
侯潇雪:模型构建,算法设计与实现,论文撰写。
方沛:论文审阅与修订。
张苗苗:论文审阅与修订,算法改进指导。

