单液流锌镍电池的四阶等效阻抗模型
宋春宁,凌旗金,苏有平,郑少耿
(广西大学电气工程学院,广西 南宁 530004)
电化学阻抗谱(EIS)在锂离子电池、全钒液流电池等各类电池的研究中已有诸多应用[1-2]。EIS数据处理,通常与等效电路模型相结合[1],但由于一组EIS数据可以通过多种不同电路结构和元件参数的等效电路来表达,要确定能真实反映系统物理化学意义的等效电路模型并不容易,往往依赖于研究人员的经验和参考文献。目前,已存在的电池典型等效电路模型[3],如Thevenin模型、新一代汽车合作伙伴计划(PNGV)模型、非线性等效(GNL)模型等,都是用一组电阻和电容的并联组合来等效代替电池的一个极化过程,包括改进的电池等效电路模型,如三阶RC网络模型[4]等,也多是依靠经验来确定电池RC并联网络的数量,而没有明确的实验参考。
基于傅里叶变换的弛豫时间分布(DRT)技术可解决上述问题,在EIS的数据解析中获得了广泛的应用[5]。弛豫时间是衡量系统的某种变量由暂态趋于稳态所需的时间。弛豫时间的分布对应特征时间常数的分布,对应不同的电化学极化过程,因此,可通过提取EIS数据的DRT分布特征,来区分不同的电化学过程,避免电化学系统模型的先验假设问题。此外,等效电路模型元件的参数并不能直接测量,需要进行辨识。参数辨识是一个不断寻优的过程。目前,已存在多种优化算法,用于电池等效电路模型的元件参数辨识,如最小二乘法[6]和鲸鱼优化算法(WOA)[7]等。WOA是一种启发式算法,通过模仿座头鲸群体捕食行为来寻找目标问题的最优解,具有结构简单、参数少及易于实现等优点。
本文作者以单液流锌镍电池为研究对象,根据电池的EIS测量结果,基于DRT技术,建立单液流锌镍电池四阶等效阻抗模型,并提出一种改进的WOA来辨识阻抗模型参数。
1 建立电池四阶等效阻抗模型
1.1 单液流锌镍电池的电化学阻抗谱测量
选用8 Ah的单液流锌镍电池(江苏产)作为实验电池,正极材料为烧结氧化镍多孔电极,负极材料为镀锌电极,电解液为10.0 mol/L KOH+0.8 mol/L ZnO+0.5 mol/L LiOH,加入量为5.0 L,流速为6.5 L/min。
用Model 350c频率响应分析仪(美国产),采用频域分析法,测量得到电池荷电状态(SOC)分别为20%、50%时,对应的EIS[1],如图1所示,频率为1~104Hz。

图1 单液流锌镍电池不同SOC下的EISFig.1 Electrochemical impedance spectroscopy(EIS) of single-flow zinc-nickel battery at different SOC
1.2 DRT技术的原理
DRT技术用无数个相互串联的RC回路代表电池内部的极化过程数目及强度,弛豫时间常数均匀分布于0~+∞。DRT技术的RC阻抗等效电路模型,如图2所示。
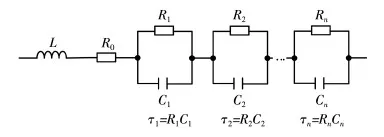
图2 DRT技术的电池等效电路模型Fig.2 Equivalent circuit model of battery in distribution of relaxation time(DRT) technique
图2中:L为等效感抗;R0为欧姆内阻;R1、R2…Rn表示n个不同的极化电阻;C1、C2…Cn表示n个不同的极化电容;τ为弛豫时间常数。
图2中等效电路模型阻抗的表达式为:
(1)
式(1)中:Z(f)为图2所示等效电路的总阻抗;i表示第i个RC并联回路;Rpol为极化阻抗;f为频率;j为复数单位;g(τ)为描述电池τ特性的特定函数,满足式(2)。
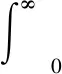
(2)
阻抗谱通常是通过对数采样,因此,式(1)可表示为以lnτ为变量的函数形式γ(τ),变换过程为:
(3)
γ(τ)=τg(τ)
(4)
式(3)中:e为自然常数。
将式(3)、(4)代入式(1),可得:
(5)
1.3 用DRT技术确定电池阻抗模型结构
基于DRT计算原理公布的开源软件,将测得的单液流锌镍电池的EIS数据导入DRTtools软件[8],设置离散化基为平均松弛时间间隔的0.2倍,选择包括电感拟合,得到SOC分别为20%和50%时对应的DRT函数曲线,如图3所示。
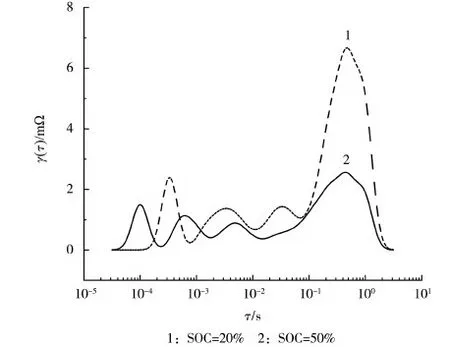
图3 电池SOC分别为20%和50%时的DRT函数曲线Fig.3 DRT function curves of battery SOC with 20% and 50%
从图3可知,得到的DRT函数曲线有4个明显的特征峰,因此,可将单液流锌镍电池的极化阻抗等效为4个串联的RC网络。据此,建立四阶等效阻抗模型电路图,如图2中n=4时所示。
由式(1)可得该模型的阻抗表达式,如式(6)所示:
(6)
阻抗的实部和虚部表达式,如式(7)、(8)所示:
(7)
(8)
2 改进的鲸鱼优化算法(GrWOA)
2.1 基本的鲸鱼优化算法(WOA)
WOA可分为包围猎物、气泡网攻击和寻找猎物等3个阶段。
①包围猎物,数学描述如式(9)所示。
X(t+1)=X*(t)-a(2r1-1)|2r2X*(t)-X(t)|
(9)
式(9)中:t是算法的迭代次数;X代表当前解;X*代表最优解;r1、r2是[0,1]的随机数。
随着迭代次数t的增加,控制系数a从2线性减小到0,函数关系如式(10)所示。
(10)
式(10)中:tMaxIter表示算法的最大迭代次数。
②气泡网攻击,数学描述如式(11)所示。
X(t+1)=|2r3X*(t)-X(t)|eb-lcos(2πl)+X*(t)
(11)
式(11)中:b是常数,取1;l和r3都是[0,1]的随机数。
③寻找猎物,数学描述如式(12)所示。
X(t+1)=Xrand(t)-a(2r1-1)|2r4Xrand(t)-X(t)|
(12)
式(12)中:Xrand是鲸鱼种群中随机选择一条鲸鱼;r4是[0,1]的随机数。
当控制参数A=|a(2r1-1)|≥1时,WOA进行全局搜索;当A<1时,WOA进行局部搜索,鲸鱼此时会以0.5的概率进行螺旋运动(气泡网攻击),以0.5的概率包围猎物。
2.2 改进的WOA(GrWOA)
为了增强基本WOA跳出局部最优的能力,提高算法收敛精度,对基本的WOA作如下改进:
①改进包围猎物过程中的控制系数a。
式(11)中,随着迭代次数t的增加,控制系数a线性减小,使得算法的全局搜索能力线性减小,局部搜索能力线性增强,容易出现早熟现象。为了避免算法过早陷入局部最优,增强算法在前期的全局搜索能力,提出一种改进半圆的控制系数策略,数学模型如式(13)所示。
(13)
在式(13)中,当a的初始值为2时,a与迭代次数t(设tMaxIter=500)的关系曲线如图4所示。
从图4可知,控制系数a非线性减小。前期a较大,算法能充分进行全局搜索;后期a急剧减小,算法具备更强的局部搜索能力,从而加快收敛速度和提高求解精度。
②改进寻找猎物过程中的控制参数A。
WOA进行局部搜索时,应该加大搜索范围,以便寻得更优的解。式(12)中,控制参数A在[-2,2]变化,虽能较好地进行全局搜索,但若解的搜索范围太大,而A的变化范围太小,很容易陷入局部最优。有鉴于此,提出一个基于改进Griewank函数[9]的Gr因子来代替A,以扩大A的变化范围,如式(14)所示。改进的Gr因子如式(15)所示。

图4 控制系数a与迭代次数t的关系曲线Fig.4 Relation curves between the control coefficient a and the number of iterations t
X(t+1)=Xrand(t)+Gr|2r4Xrand(t)-X(t)|
(14)
Gr(x)=x3(2r1-1)-cos(x)+1
(15)
式(15)中:x是Gr函数的自变量,是采用MATLAB中的randn函数产生的随机数。
为获取Gr因子的波动范围,进行3 000次迭代,即x=randn(1,3 000),得到改进的Gr因子分布图,如图5所示。

图5 改进的Gr因子迭代3 000次的数值分布图Fig.5 Improved Gr factor distribution map for 3 000 iterations
从图5可知,改进的Gr因子以较大的概率在[-5,5]波动,扩大了A的变化范围。
为进一步提高算法跳出局部最优的能力,将改进的Gr因子引入式(11)中,进一步提高GrWOA的优化性能,数学描述如式(16)所示:
X(t+1)=Gr|2r3X*(t)-X(t)|eb-lcos(2πl)+X*(t)
(16)
2.3 GrWOA验证分析
为验证GrWOA的改进有效性,选取6个标准shifted测试函数进行仿真实验,测试函数见表1。单峰函数F1~F2用于测试算法的收敛速度和收敛精度;多峰函数F3~F6用于测试算法跳出局部最优的能力,各函数搜索最优值均设为0。

表1 6个标准shifted测试函数Table 1 Six standard shifted test functions
表1中:xi为第i维解向量;oi为第i维偏移量;zi为二者的差值,表示对函数的解设置偏移。
将GrWOA与基本的WOA分别用于6个标准shifted测试函数。实验设置为:种群规模N=50;最大迭代次数tMaxIter=500×N;偏移量oi(i=1,2…n)为搜索范围内的随机值,搜索维度n=20。将两种算法分别独立对表1的6个标准shifted测试函数运行51次,记录求解最优结果的平均值(Ave,反映算法的求解精度)和标准差(Std,反映算法的求解稳定性)。仿真实验结果如表2所示。

表2 仿真实验结果Table 2 Simulation experiment results
从表2可知,GrWOA求解结果的平均值与标准差均小于WOA,证明了算法改进的有效性。
3 GrWOA辨识电池四阶等效阻抗模型参数
3.1 建立阻抗模型参数辨识的适应度函数
单液流锌镍电池的四阶等效阻抗模型的元件参数辨识目标是寻求一组最优的参数集合[R0,R1,C1,R2,C2,R3,C3,R4,C4,L],使该电路模型总阻抗的实部与虚部更接近测量得到的阻抗实部与虚部。建立参数辨识的适应度(目标函数)公式,如(17)所示:
(17)

用GrWOA辨识四阶等效阻抗模型参数的流程,如图6所示。
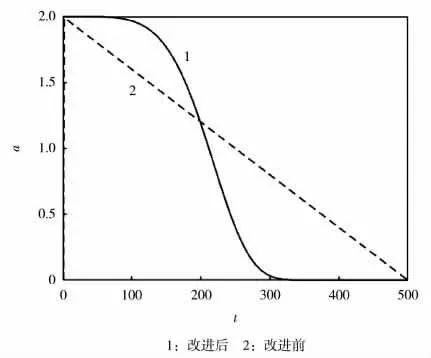
图6 GrWOA辨识阻抗模型参数流程图Fig.6 Flow chart of parameter identification of impedance mo-del by GrWOA
3.2 阻抗模型参数辨识的结果分析
导入测量得到的电池阻抗谱数据,设置GrWOA的种群规模N=100,最大迭代次数tMaxIter=500×N,搜索维度n=10。按图6流程辨识得到电池四阶阻抗模型参数,如表3所示。

表3 单液流锌镍电池阻抗模型参数辨识结果Table 3 Impedance model parameter identification results of single flow zinc-nickel battery
将表3中的结果代入四阶等效阻抗模型,计算得到电池的EIS,如图7所示。

图7 电池不同SOC下辨识与实测的EIS对比图Fig.7 EIS comparison diagram of battery identification and measurement at different SOC
从图7可知,四阶等效阻抗模型计算得到电池的EIS,与实测的EIS的重复性较好。
进一步求取该模型参数辨识的平均相对误差和均方根误差,如表4所示。
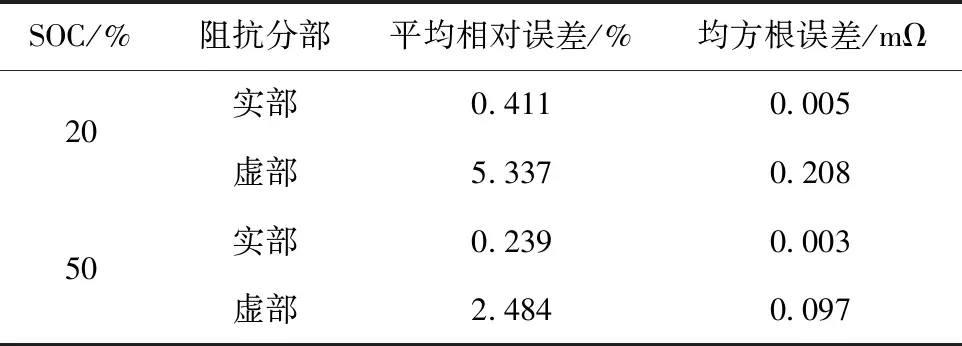
表4 GrWOA辨识阻抗模型的参数误差Table 4 Parameter error of identification impedance model by GrWOA
从表4可知,实部平均相对误差在1%以内,均方根误差小于0.005 mΩ;虚部平均相对误差在6%以内,均方根误差小于0.300 mΩ,说明GrWOA辨识得到的电池四阶等效阻抗模型有较高的精度。
4 结论
本文作者以单液流锌镍电池为研究对象,测量得到电池SOC分别为20%和50%时的EIS。根据EIS测量结果,用DRT技术建立单液流锌镍电池四阶等效阻抗模型,为使用先验知识确定电池等效电路模型结构不够精确的问题,提供可行的实验解决方案。提出一种改进的鲸鱼优化算法(GrWOA),用于电池四阶等效阻抗模型的元件参数辨识,用6个标准的shifted测试函数验证GrWOA的改进效果。仿真结果表明,辨识出来的EIS与实验测试得到的EIS数据拟合良好。辨识得到的阻抗实部数据平均相对误差小于1%,虚部数据平均相对误差小于6%。
该方法可以测量更多单液流锌镍电池不同SOC下的EIS,建立对应的等效电路模型,通过研究等效电路模型的元件参数变化规律,进一步研究电池的电极反应动力学过程。

