质子交换膜燃料电池活化性能快速分析方法
汪殿龙,王梓鉴*,杨代军,程旭峰
(1.河北科技大学材料科学与工程学院,河北 石家庄 050018; 2.同济大学汽车学院,上海 201804;3.河北科技大学机械学院,河北 石家庄 050018)
实际应用时,刚组装的质子交换膜燃料电池(PEMFC)性能较差,为提高性能,需要使用一系列的方法来活化[1]。要确定更优的活化工艺,快速获得电池内部关键位置(膜和催化剂)的电化学行为很重要。目前,此工作主要通过电化学测试方法完成,如电化学阻抗谱(EIS)、循环伏安(CV)和线性伏安扫描(LSV)法等。这些方法虽能直接反映PEMFC活化性能的变化,但存在步骤繁琐、耗时较长等缺点,限制了PEMFC活化工艺的研究和探索。
目前,本文作者还未见到使用智能算法进行活化分析的文献报道,但该方法在原理上与PEMFC模型优化或性能预测类似。目前使用较多的智能算法可大致分为群体智能算法、进化算法和人工神经网络算法等3类。M.Y.Ye等[2]使用惯性权重线性下降的粒子群优化算法(PSO)优化PEMFC模型参数,并进行抗噪声测试,认为该方法是有效的燃料电池参数识别技术,且在一定的测量噪声下,依然表现良好。Y.Cao等[3]在海鸥优化算法(SOA)中加入莱维飞行(个体移动步长较大概率出现大跨度步长)机制,以加快算法的收敛速度。在同一种电池系统上,优化后的算法经22次迭代后的误差平方和(SSE)为2.18,而标准SOA经80次迭代后的SSE为2.21,优化后的算法在求解质量和收敛速度方面有明显提升。U.K.Chakraborty等[4]使用改进的差分进化(DE)算法优化PEMFC参数,在高低噪音下的结果显示,相比几种标准DE变体和遗传(GA)算法,改进DE算法在500 000次迭代后的适应度值、达到目标适应度的迭代次数和运行时间等3个方面至少有一个优于其他几种算法。T.Wilberforce等[5]使用改进的人工神经网络(ANN)算法拟合PEMFC的极化曲线,并预测性能,使用的两种神经网络模型虽然有差异,但都能取得相对满意的结果。上述算法中,群体智能算法的收敛速度较快,但存在解精度低、容易陷入局部最优的缺点,解的一致性较差[6];人工神经网络通常需要大量的数据和高成本的计算。这些缺点在一定程度上限制了群体智能算法和人工神经网络在PEMFC活化分析中的应用。综上所述,DE算法更符合分析方法的要求。
为减少PEMFC关键位置电化学行为的获取时间,快速获得有关PEMFC活化状态及有效性的信息,本文作者提出一种基于智能算法的快速分析方法,利用DE算法进行PEMFC活化的快速性能分析。首先进行PEMFC的活化实验,再分析相关的实验结果,最后验证该方法的可行性。
1 快速分析方法
活化性能快速分析方法的结构见图1。

图1 快速分析方法的结构图
该方法需要一个PEMFC模型、DE算法和不同活化时间节点的极化数据。通过PEMFC的活化和极化实验,得到极化数据,再利用DE算法和PEMFC模型分析不同活化时间节点的极化数据,最终得到活化性能。
1.1 PEMFC模型
PEMFC常用的数学模型见式(1)。
Ucell=E0-ηohm-ηact-ηconc
(1)
式(1)中:Ucell为电池电压;ηohm、ηact和ηconc为当电池有负载时的3个电压损失,即欧姆损失、活化损失和浓差损失;E0为开路电压。
1.1.1 欧姆损失ηohm
PEMFC的欧姆损失ηohm包括电流穿过双极板及外部总线的电子电阻和膜对离子流的离子电阻。
由于活化过程中电子电阻几乎不发生变化,可将ηohm的等效电阻用面积比电阻r表示,以反映膜的变化。ηohm与电流密度J的关系见式(2)。
ηohm=J·r
(2)
1.1.2 活化损失ηact
电极上发生反应所需要的能量体现为部分电压损失,即活化损失,主要集中在低电流区域。
活化极化损失方程通常由塔菲尔方程推导出,见式(3)。
(3)
式(3)中:A为塔菲尔斜率;J0为交换电流密度,可作为判断电化学反应催化剂活性的指标。
1.1.3 浓差损失ηconc
电池电流较大时,电极附近的反应物浓度低于入口浓度,会造成部分电压损失,即浓差损失。通过能斯特方程和菲克扩散定律,可得到浓差极化的电压损耗关系,见式(4)。
(4)
式(4)中:B为浓差损失常数;JL为当燃料以最大速度供应时,燃料电池所能达到的极限电流密度。
1.1.4 目标函数
PEMFC的极化曲线是常用的稳态性能指标,通常由即时测量随电流变化的电池电压得到。
通过DE算法来最优搜索PEMFC数学模型的参数,目标函数见式(5)。
(5)
式(5)中:N为数据数量;Up(m)为PEMFC模型所得到的第m个模型的电压;Udata(m)为每次活化循环后极化实验的第m个实验数据。Up由式(1)计算,使用6个差分进化参数(A、J0、JL、E0、B和r)。
1.2 差分进化(DE)算法
DE算法的原理,是从设定边界中随机产生种群开始,在优胜劣汰的规则下,通过不断地迭代进化,引导搜索过程向全局最优值逼近。对于PEMFC的参数最优搜索问题,适应度函数即为目标函数式(5),目标函数的值越小,个体的适应度越好。用于本策略的DE算法可描述为以下步骤。

(6)
步骤②:变异。变异操作有多个版本,实验调用的特定版本是DE/rand/1/bin,即随机选择3个不同的个体(用p1≠p2≠p3表示不同),将其中任意两个向量的差值进行缩放并与另一向量求和,产生变异个体Hj,G+1,见式(7)。
Hj,G+1=Vj,0(p1)+F·[Vj,0(p2)-Vj,0(p3)]
(7)
式(7)中:F为缩放因子;G为当前进化代数。
变异过程中要判断变异后的个体是否满足边界条件,若不满足,需要再次随机生成(同步骤①)。F的取值会影响结果,当取值较小时,种群之间的差异度小,容易出现“早熟”现象(早期某一个体适应值大幅超过平均个体适应值)。为避免“早熟”现象,加入具有自适应特性的变异算子[7],自适应算法见式(8)、(9)。
(8)
F=F0·2λ
(9)
式(8)-(9)中:λ为中间变量;F0为变异算子;Gm代表最大进化代数;e为自然常数。自适应算法使F在进化初期值较大,可避免过早收敛,保持种群多样性;随着进化进行,F逐渐变小,在后期接近F0,保留最优信息,增加全局最优收敛的概率。
步骤③:交叉。在变异后的个体Hj,G+1和初始个体Vj,G中,任意选择“染色体”中的“基因”(个体向量中的某一解)组合成新的个体Kj,G+1,如式(10)所示,其中Cr表示交叉概率。为确保变异个体向量至少有一个“基因”能传给下一代,交叉操作的初始是在变异个体中随机选取第drand位“基因”,作为交叉后新个体的第drand位“基因”。
(10)
步骤④:选择。DE算法的选择操作使用贪婪算法,将当前向量与初始向量的适应度进行比较,总是选适应度最优的那个向量个体,见式(11)。此处选择结果取决于适应度函数式(5)。
(11)
步骤⑤:转到步骤②,重复迭代,直到满足停止条件。
DE算法的停止条件,通常是设置最大迭代次数或适应度小于设定值。
2 实验
实验装置包括G20实验平台(Greenlight公司)和自制0.1 V/300 A可控电子负载。膜电极组件(MEA)G1.0-35B(河南产)由M735.18质子交换膜、催化剂层(CL)和气体扩散层(GDL)组成,详细参数见表1。MEA放置在两个有蜿蜒气体通道的石墨板中间,然后压在两块镀金铜板之间,GDL由碳纸制成。G20实验平台设有反应物气体的加热加湿系统和电池的温控器。采用一系列的脉冲电流进行活化,设定脉冲电流周期为10 s,占空比为20%,电流形式见图2。活化实验条件如下:阴、阳极压力分别为120 kPa、140 kPa,电池温度为85 ℃,阴阳极相对湿度均为80%。
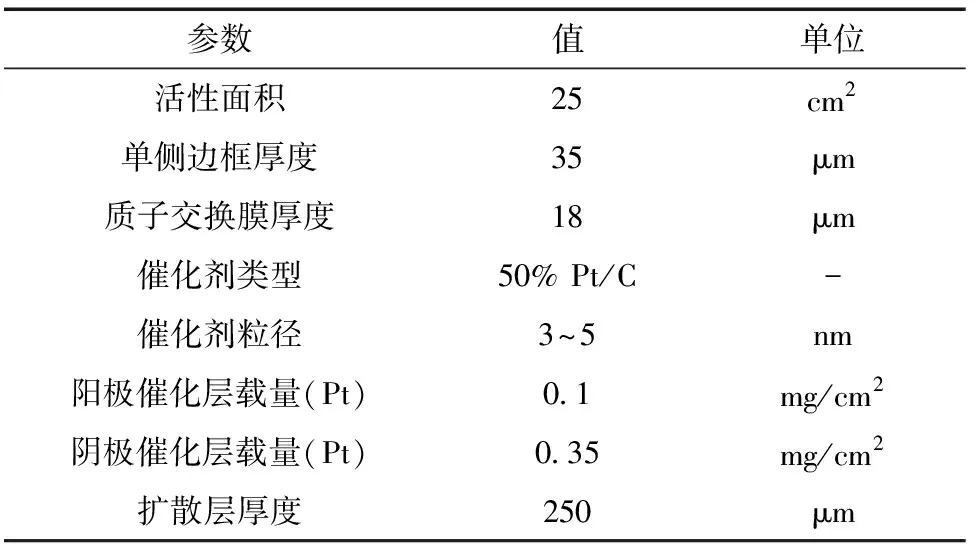
表1 MEA的详细参数

图2 PEMFC活化脉冲电流波形
实验只考虑脉冲电流活化对燃料电池性能的影响。活化后,燃料电池停止工作并冷却。随后进行极化测试,测试条件如下:电池温度为75 ℃,露点温度为60 ℃,阴、阳极压力分别为80 kPa、100 kPa,气体相对湿度为50%,氢/空气的化学计量比为1.7/3.0。在不同的活化时间点,连续测量PEMFC的电流和电压,得到一系列极化曲线。
EIS测试在Reference 3000电化学工作站(美国产)上进行,交流信号振幅为工作电流的5%。EIS测试在每次极化测试之后进行,电池操作条件与极化测试一致。基于EIS结果,由等效电路模型拟合可获得欧姆阻抗Rohm、电荷转移阻抗Rct和传质阻抗Rmt,恒相位元件CPE主要描述双层电容的行为,电荷传输和质量传输分别对应一个双层电容,即CPEct和CPEmt。CPE包括两个参数,CPE-P表示原件特性偏离纯电容的程度,当取值为1时,恒相位原件等效为电容;CPE-T可表示等效电容的大小。EIS的测试数据通过Zview软件进行等效电路模型分析,等效电路模型如图3所示。
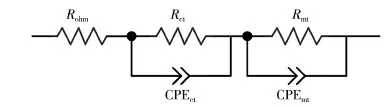
图3 EIS分析的等效电路模型
3 结果与讨论
采用活化过程中不同时间点的极化实验数据,评价DE算法的识别能力。比较活化初始、活化后1 h和活化后2 h电池的优化参数值,来分析活化的机理,并从拟合后J-U曲线的形状、适应度值和EIS测试,评价所提方法的有效性。
DE算法中的控制变量设置为种群大小Np=70,交叉概率Cr=0.8和最大进化次数5 000次。缩放因子F由自适应的变异算子得到,设定变异算子F0=0.5。算法参数的设定与文献[4]的推荐值相同,参数的大小与实际问题无关。每个DE种群表示一组燃料电池参数,模型参数的搜索范围根据物理意义来设置。DE算法通过MATLAB软件实现。
活化初始、活化1 h及活化2 h后PEMFC的极化曲线和功率密度曲线如图4所示。

图4 极化曲线和功率密度曲线
从图4可知,当电流密度大于1 700 mA/cm2时,PEMFC的性能相对不稳定,主要原因是阴极侧产生大量的水。活化1 h后,PEMFC的最大功率密度提升了21.7%。
不同活化时间节点DE算法的收敛过程见图5,DE算法识别结果见表2。从表2可知,活化1 h后,与活化初始相比,E0、J0、B和JL增加,r、A减小。当在不同的活化时间点下达到最大进化次数时,DE算法可得到一个较小的目标函数值Ffit,且均小于5.5×10-3,说明使用DE算法对实验数据进行参数搜索是可行的。从这些参数的物理意义可判断,脉冲电流能通过提高催化剂的活性和膜的渗透率,降低膜的离子阻抗,减少3个极化区域的电压损失。比较活化1 h和2 h的参数变化可知,r继续减小,原因是膜的离子阻抗通常是膜中含水量的函数,表明膜的水化程度随活化而增加。实验发现A增加、J0减小,表明活化损失增加,与传统观点不同,且在文献[8]中已有报道。可变电流的活化被认为可在催化剂层上形成孔隙,特别是随着电流的增加,孔隙将逐渐渗透到内部。氢分子很容易通过孔隙,不容易被Pt/C粒子捕获,暗示了电化学活性面积减小,即活化损失增加[8]。此外,实验还发现B增加、JL减小,表明过度活化可能使浓差损失增加。

图5 不同活化时间节点DE算法的收敛过程

表2 DE算法识别结果 Table 2 Recognition results of DE algorithm
实验数据与从DE优化模型中得到的J-U特性之间的比较如图6所示。
从图6可知,虽然实验数据与DE算法优化模型存在一定的误差,但拟合效果可以接受。
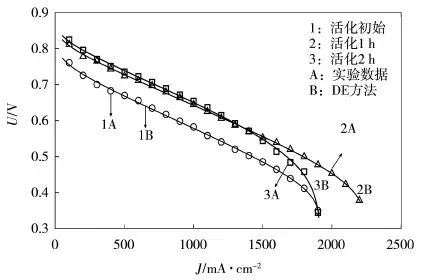
图6 DE算法优化模型与实验数据的比较
实验主要通过EIS测试验证DE算法最优搜索结果的有效性。由于是在不同条件下得到的结果,EIS和算法分析数据不能直接进行定量比较,但可通过相关参数的变化定性验证。利用DE算法进行基于实验数据的参数搜索的任何进展都非常重要,原因是有利于识别结果更加接近实际值。
图7为800 mA/cm2下不同活化时间点的奈奎斯特图。
图7中的曲线都由高频区域和低频区域的两个弧组成。高频区域(靠近虚轴)的弧通常与MEA中的电荷动力学有关,低频区域(远离虚轴)的弧通常与氧传质阻抗有关。活化在1 h后基本完成,因为此时高低频圆弧半径均最小,即电荷转移阻抗和氧传质阻抗均最小。
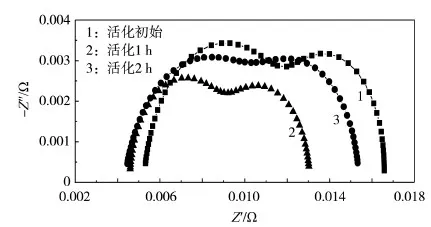
图7 800 mA/cm2下不同活化时间点的奈奎斯特图
等效电路的拟合结果详见表3。
从表3可知,PEMFC的Rohm、Rct和Rmt在活化1 h后达到一个较小值,表明脉冲电流活化方法可从3个极化区降低PEMFC的电压损失。在活化2 h后,Rohm继续下降,但Rmt和Rct增加。这表明,一方面电池的活化时间越长,膜的水化程度越高;另一方面,挖掘效应阻碍了Pt/C粒子捕获氢分子,且长期高温高压活化使电池内部压力加大,阻碍了氧的传质,导致较高的活化损失和浓差损失[9]。在耗时方面,极化测试在活化研究中几乎是必要的,因此不予考虑。

表3 不同活化时间点等效电路的拟合结果 Table 3 Fitting results of equivalent circuits at different activation time points
EIS与基于DE算法的快速方法的结果比较见表4。

表4 EIS与基于DE算法的快速方法的结果比较
从表4可知,基于DE算法的快速方法比EIS测试约快40倍。另外,EIS分析结果与算法分析得到的结果一致,验证了所提出的基于DE算法的PEMFC快速活化性能分析方法具有一定的可行性。
4 结论
本文作者提出一种PEMFC活化性能快速分析方法,并通过实际活化实验及EIS测试,验证该方法的可行性。
实验结果表明,活化1 h后,MEA在活化损失、欧姆损失和浓差损失等方面降低了相应的电压损失。长时间的活化对燃料电池有负面影响,虽然很难在极化曲线中体现,但算法结果和EIS分析均说明,长时间活化后,尽管欧姆损失仍减少,但浓差损失和活化损失增加。此外,常用的燃料电池测试方法繁琐且耗时较长,而该方法仅在10 s内通过J-U曲线快速分析燃料电池,结果质量较高,很适合活化性能的初步评估,有利于快速确定更好的活化工艺及参数。

