离子选择性表面电对流的多块LB 模拟1)

张 煜 李天富 罗 康 吴 健 易红亮,2)

* (哈尔滨工业大学能源科学与工程学院,空天热物理工信部重点实验室,哈尔滨 150001)

†(季华实验室,广东佛山 528000)

引言

近几十年来,随着微机电加工技术的迅速发展,基于电流体动力学进行流动控制逐渐成为微尺度下介质操控的一种重要方式.当介电液体与离子选择性材料(例如纳米通道、离子交换膜等)相接触,在外加电压的作用下,会产生离子浓差极化(ion concentration polarization,ICP)现象,且在较高电压下还会产生复杂的对流现象,即所谓的第二类电渗流或离子交换表面的电对流.这一类问题在海水淡化、离子浓度富集、燃料电池等诸多领域具有广泛的应用前景[1-4].

向带有离子交换表面的电解质溶液施加电压,通过交换表面的电流会呈现出复杂的非线性变化过程.图1 给出了典型离子交换膜系统的电流-电压特性示意图.随着垂直施加在流体与离子交换膜表面的电压逐渐增大,通过电解质溶液的电流会经历三个阶段: 欧姆区(Ohmic regime),电流先随着电压的增大而明显增大;饱和区(limiting regime),电流不随电压发生明显变化;过饱和区(over-limiting)[5]电压继续增大,电流随电压再一次出现增大的趋势.

这些特性与系统内离子输运机制随电压的变化有关[6].在离子交换膜表面施加电压,异号离子被表面吸收,同号离子因电场力排斥远离表面,形成双电层(electric double layer,EDL),如图2 中曲线I1.随着外加电压增大,电场对同性离子的排斥增强,双电层外的离子浓度降低并形成浓差极化区.极化区的离子浓度主要由远离表面的离子通过扩散作用进行补充,因此双电层外部的离子浓度呈线性分布,形成电中性的外部扩散层(diffusion layer,DL),如图2 中的曲线I2.当外加电压增大到一定值时,离子膜表面同性离子被耗尽,如图2 中曲线I3,介电液体表现出很高的电阻,电流几乎不再随电压增加,与图1 中的饱和区相对应所示.Levich 等[7]以带有单种阴阳离子的稀溶液为模型进行分析,获得这一饱和电流理论解Ilim=2zeDC0/L,其中z表示离子价,e为元电荷密度,D为离子的扩散系数,C0为边界处于稳定状态溶液的浓度,L为离子交换表面到与主体溶液浓度相等界面的距离.

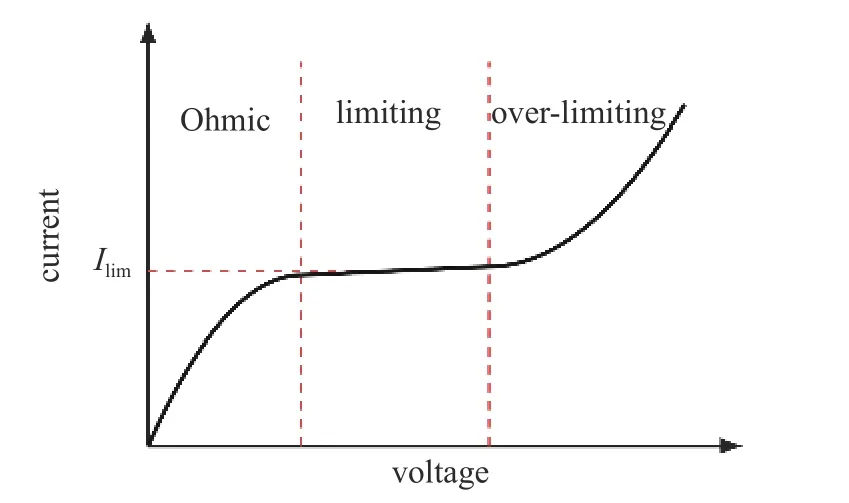
图1 离子交换膜表面电流-电压特性示意图Fig.1 A schematic voltage-current characteristics near ions selective surface

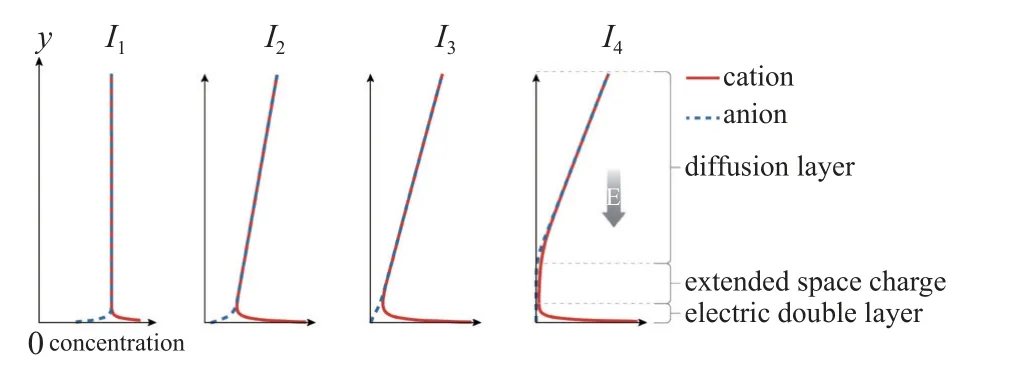
图2 离子交换表面的浓差极化特性曲线[5]Fig.2 Ion concentration polarization on ions selective surface[5]

由于离子交换表面的存在,壁面附近同性离子浓度随电压的增大最终趋于零,而双电层外部出现扩展空间电荷(extended space charge,ESC) 层.ESC 层外离子输运仍保持扩散层特性.已有结果表明,在ESC 层与DL 层之间还存在一个过渡层(transition layer,TL)[6],如图2 中曲线I4.当外加电压超过某一临界值,ESC 层变得不稳定,触发电对流,离子浓度分布达到新的平衡.

关于离子交换表面的电对流问题研究已久.近年来随着计算技术的发展,数值模拟成为一种有力的研究手段.多位国内外学者采用诸如谱方法[8]、有限体积[9]、有限元[10]等算法对此类问题进行数值模拟.格子Boltzmann 方法(lattice Boltzmann method,LBM)作为一种介观方法,自诞生以来,以其易于编程、适合复杂形状与并行计算、适合多相、多物理场耦合的模拟等优势,被迅速扩展应用至复杂流动、传热传质、多相及多场耦合流动等领域[11-14].本文采用LBM 数值求解这一问题.

应用LBM 求解电流体力学问题由来已久.最初有学者利用Poisson-Boltzmann (PB)模型求解了微通道内的电渗流问题[15-18].2010 年,Wang 等[19]提出了完全求解Poisson-Nernst-Planck (PNP)模型的电流体力学LBM 求解模型.随后,不断有学者提出并改进基于LBM 的PNP 电场求解模型,用于研究单极注入电荷表面电(热)对流[20]、电场强化相变[21]等电流体问题.

本文提出一种基于多块网格的LB 模型来模拟离子选择性表面的电对流问题.采用不同的LB 输运方程对多物理场进行耦合,并给出了局部加密的多块LB 信息交换格式.由于本文所考虑的物理问题在边界双电层内有很大的浓度梯度,且需要耦合求解离子输运、流动以及电势等控制方程,该局部加密的LB 格式适合本问题的求解.随后,利用发展的LB 方法数值求解Navier-Stokes (N-S) 方程、PNP 方程互相耦合的电流体力学控制方程组,模拟了离子选择性表面的电对流问题.

本工作有两个难点: 一是表征离子输运的NP方程的强对流占优使多个物理场的耦合变得不稳定;二是离子交换表面电荷浓度在很小的范围内迅速衰减导致的大浓度梯度.针对前者,采用多弛豫时间(multi-relaxtion time,MRT) 模型以保证模型的稳定性;对于后者,采用多块网格局部加密来克服标准LBM 均匀网格的不足[22].本文的结构安排如下: 第一节对物理及数值模型问题进行介绍;第二节给出了本文提出的多块LB 电流体力学求解模型;第三节利用本文提出的多块LB 模型模拟了离子交换表面的电对流问题;最后对文章内容做了总结与展望.

1 数学物理模型

1.1 宏观控制方程

本文研究的物理模型如图3 所示.求解区域内充满电解质溶液,下方覆有离子交换表面并施加电压.随着电压的增大,交换表面极性相同的离子浓度被耗尽,在壁面处积累大量的净电荷,产生库仑力,并引起流动.模拟区域中,离子交换表面被认为是无滑移壁面;上边界为静止溶液界面,数值处理格式与无滑移壁面一致;左右两侧数值上设为周期性边界.

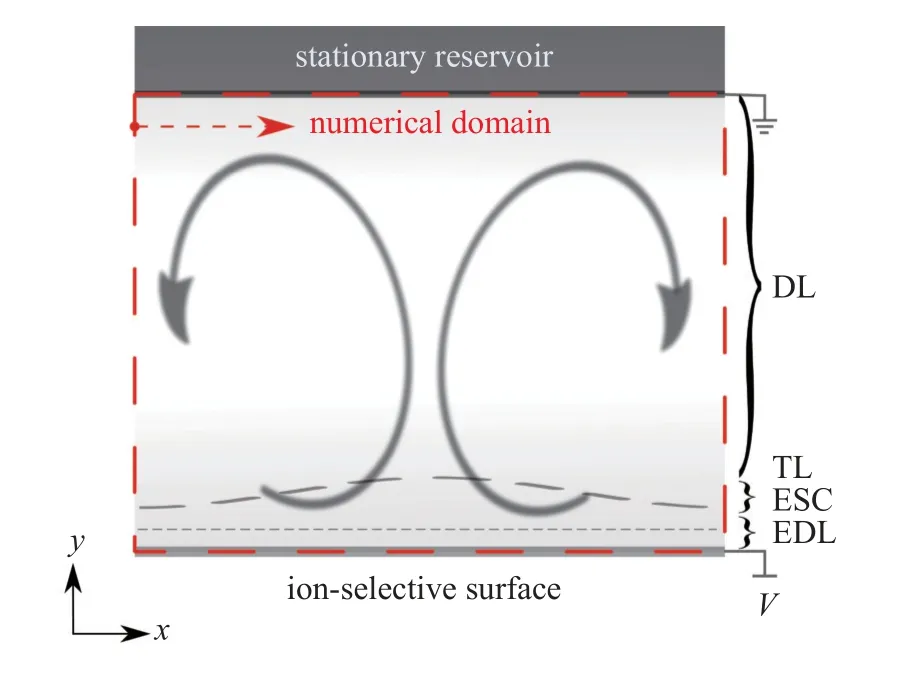
图3 离子选择性表面的电对流物理模型示意图Fig.3 Illustration of physical model for electroconvection near ions selective surface

对应的控制方程包括以下N-S 方程组、Poisson方程以及NP 方程组[9]

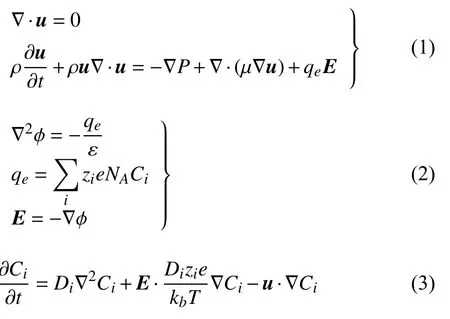
其中,符号t,u,ρ ,μ,E,Ci,Di,ε,zi,T,φ 分别代表时间、流动速度矢量、流体密度、动力黏度、电场强度、离子浓度、电荷扩散系数、电解质溶液的介电常数、离子价、温度和电势,e和kb分别为元电荷量和玻尔兹曼常数,角标i表示第i种离子.本文考虑对称二元单价离子的电解质溶液,i代表电荷的极性,z+=1,z-=-1.离子选择性表面速度为无滑移边界,施加固定负电势.假设表面为理想离子膜,不考虑阴离子对膜内离子浓度的影响,设置阳离子浓度为定值[23],阴离子通量为零

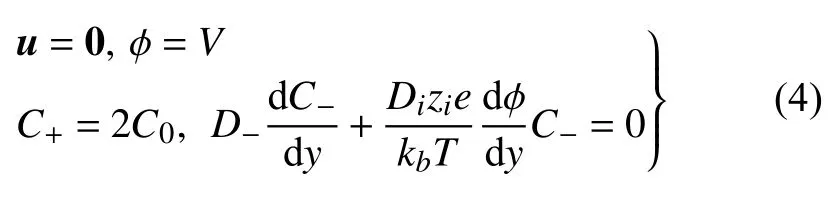
远离离子交换表面的上边界为静止状态的电解质溶液,流动速度为零,阴阳离子浓度相等

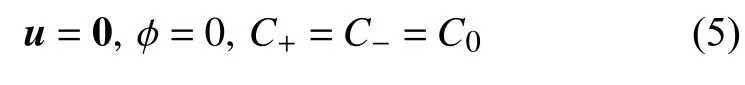
下面对LB 求解以上方程式(1)～式(3)进行介绍.LBM 的基本建模思想是采用Chapman-Enskog 多尺度分析展开Boltzmann 方程,并满足一定的宏观物理量到介观分布函数的对应关系,使得实际求解的格子离散Boltzmann 方程能够恢复成原始的宏观方程.方程求解的基本思路包括碰撞(弛豫迭代)和迁移,采用显式时间步进的方程来依次求解不同的控制方程并耦合.本文对2D 问题做模拟,下面分别给出不同宏观方程的具体LB 格式.

1.2 Navier-Stokes 方程组的LB 求解格式

采用单松弛的BGK 方程[24-25]求解控制流动的N-S 方程,方程中的外力项采用Guo 等[26]提出的外力模型

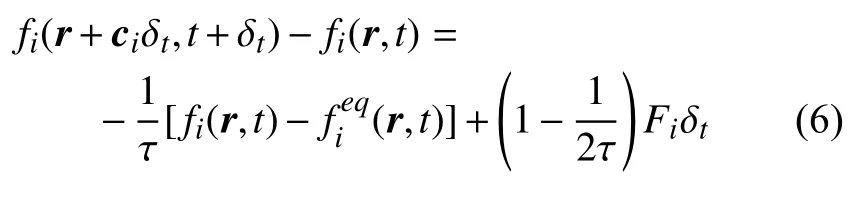
其中fi表示分布函数; δt表示格子单位下的离散时间步长;ci为格子离散速度,采用一般的D2Q9 格式[12];弛豫时间和平衡态分布函数以及外力离散由下式给出

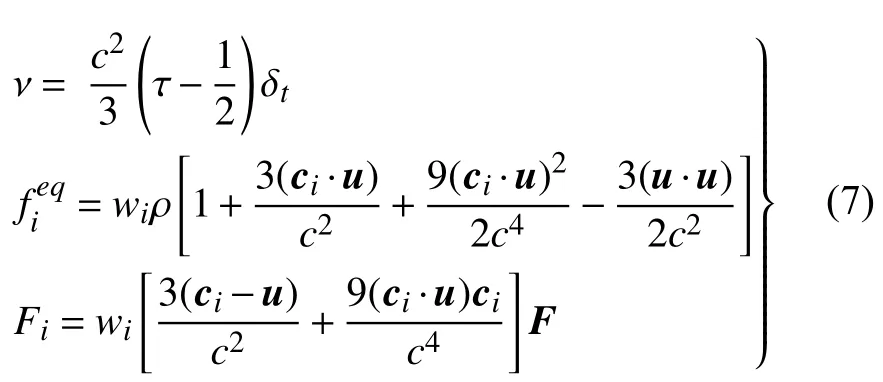
宏观量密度和速度由下式给出

式(7)和式(8)中,外力F对应于式(1)中的外力项.

1.3 Poisson 方程的LB 求解格式

采用LBM 求解Poisson 方程有多种思路.例如给Poisson 方程添加时间项,将椭圆型方程化为抛物型方程,步进迭代得到的稳态解即为原Poisson 方程的解.本文使用由Chai 等[27]提出的更接近椭圆型方程本质的一种LBM 求解格式,采用D2Q5 离散格式,碰撞项采用单松弛格式

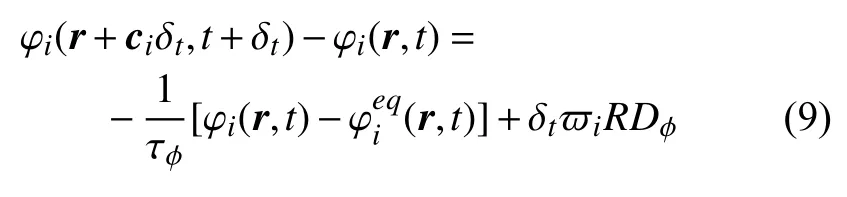
其中 φi表示电势的介观分布函数,ci为格子离散速度;人工扩散系数Dφ、弛豫时间 τφ、权重因子ϖi的表达式如下

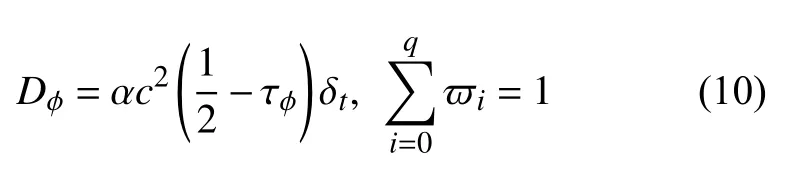
其中,α=1/2 .电势宏观量计算过程为

权重因子wi=ϖi=0,(i=0);1/4,(i=1-4) .平衡态分布函数为

关于这一Poisson 方程的求解格式,Liu 等[28]在工作中予以改进,本文采用基础格式可满足需求.

1.4 Nernst-Planck 方程的LB 求解格式

本文求解离子浓度分布的Nernst-Planck 方程的LB 格式选用Chai 等[29]提出的对流扩散方程的MRT 格式,电场输运项的处理与Luo 等[20]一致.采用D2Q9 离散,格子速度离散方向与1.2 节NS 方程的LB 格式一致,具体的多松弛演化方程如下

式中 φk表示该对流扩散方程的介观分布函数,M为从速度空间到矩空间的转换矩阵,S为弛豫矩阵,是一个微分算子.平衡态分布函数为

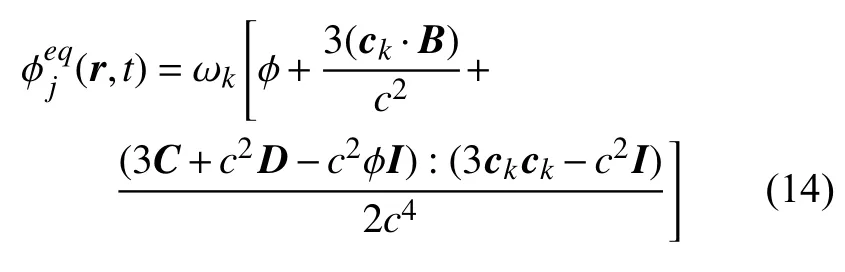
其中

分布函数到矩空间的转换关系由下式给出

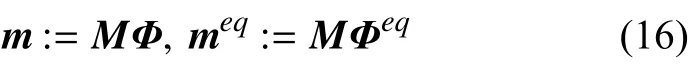
关于弛豫矩阵和转换矩阵的选取,以及对该数值格式更详细的介绍可参阅文献[29].

1.5 LB 边界条件

流场的无滑移边界条件采用Zou-He 边界(非平衡反弹格式)[30],将分布函数分为平衡态和非平衡态两部分,仅对非平衡态执行反弹.离子浓度和电势采用Guo 等[31]提出的非平衡外推格式.对离子流通量边界条件,可通过求解边界离子浓度微分方程(4),获得边界处的离子浓度[32],进而将Robin 边界转化为Dirichlet 边界条件.

2 多块LB 局部加密算法介绍

如图2 所示,在离子交换表面附近,离子浓度变化很大,在扩散层中线性分布,这样剧烈的物理量的变化对计算网格要求很高.针对离子交换边界附近很大的物理量变化,本文引入多块网格来加密边界附近的计算域,以减少网格消耗.

下面以图4 为例进行说明.AB为细网格边界,MN为粗网格边界,模拟宏观物理量在粗细网格交界面处应该保持一致.对于介观分布函数,由于LBM算法的实施由碰撞和迁移两步组成,碰撞过程只涉及当前节点的格子信息,而迁移会用到相邻格点的分布函数,因此,分布函数在网格交界处的交换应在碰撞之后、迁移之前完成,保证在每个边界处迁移进入多块计算域的分布函数信息正确和网格无关性.因此,需要推导适用于三个不同的LB 方程的信息交换格式.

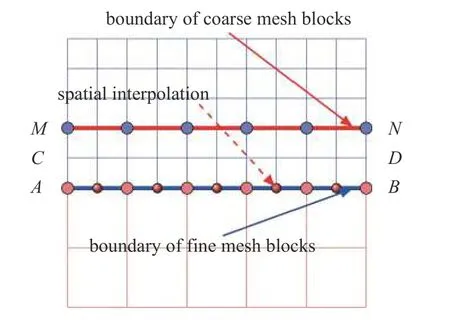
图4 多块网格加密示意图Fig.4 A sketch of multi blocks refinement

下面用下标c表示粗网格,f表示细网格(下同).若粗细网格空间离散步长之比为m=δxc/δxf,为保证分布函数的同步迁移和物理量输运的一致性,表征分布函数迁移速度的格子速度c=δx/δt以及表征物理量输运的黏度和扩散系数应保持一致.根据黏度、扩散系数与弛豫时间的关系,以及格子时间步长满足关系 δtc/δtf=m,细网格执行LBM 碰撞过程的弛豫时间也应该满足 τf=1/2+m(τc-1/2)[22].至此,每次碰撞的弛豫参数得以保证,下面给出利用多尺度分析得到的信息交换格式.

2.1 流场N-S 方程的LB 网格信息交换格式

对求解N-S 方程的LBM 分布函数做Chapman-Enskog 展开

由于上式左边外力以及导数项与时空离散格式无关,且平衡态分布函数只由宏观量决定,而宏观量应在粗细网格中保持一致,因此粗细网格的分布函数只需满足关系

将非平衡态引入式(6),格子碰撞过程可以写为

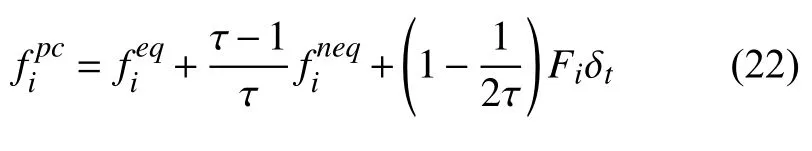
其中,上标pc代表碰撞后的量,结合式(21) 与式(22),可得

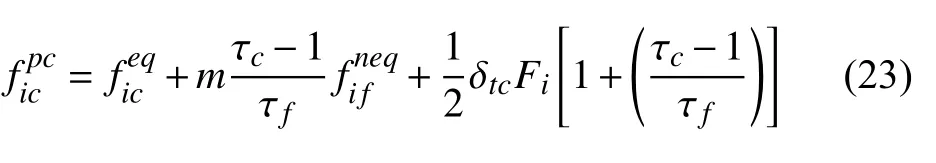
根据式(22),分布函数的非平衡态部分可以写为

将式(24)代入式(23),可得细网格向粗网格的分布函数信息交换格式

同理,可得粗网格向细网格的信息交换格式

式(26)右侧的分布函数应经过时间和空间插值之后,再通过上式从粗网格转换到细网格.

2.2 电势Poisson 方程的LB 网格信息交换格式

Poisson 方程的LB 格式已由式(9) 给出,对不同网格尺度的LB 演化方程,应保证格子声速和人工扩散系数一致,相应的弛豫时间的表达式已由前文给出.对Poisson 方程的分布函数做Chapman-Enskog 展开

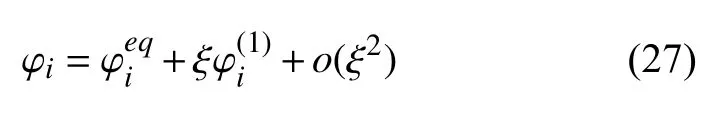
再对式(9)左侧第一项做泰勒展开并结合式(27),其中 ξ 作为一个小量,可令 ξ=δt[33],有

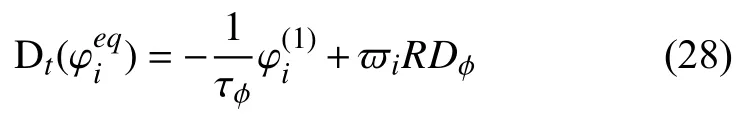
由于 ϖiRDφ-具网格无关性,为保证分布函数在粗细网格中保持一致,只需满足

又因为

可得细网格到粗网格的信息交换方程

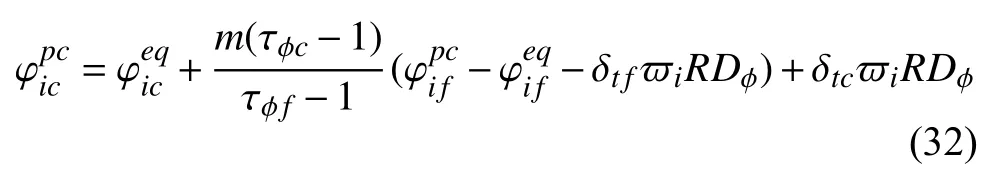
同理,分布函数由粗到细网格的交换格式为

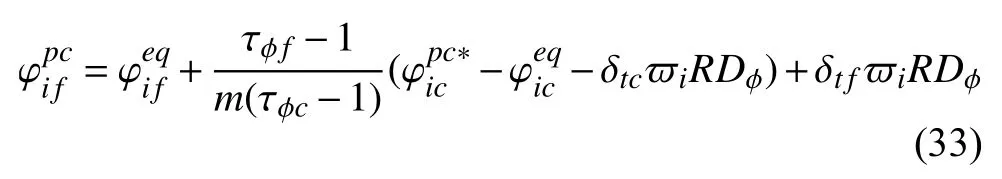
2.3 离子输运方程的LB 网格信息交换格式

对于多松弛的对流扩散模型,网格加密算法的实施依然应从Chapman-Enskog 展开导出,式(13)的详细信息及多尺度展开实施方法可参阅文献[29],这里仅给出LB 方程在矩空间展开到不同阶数并化简之后得到的结果

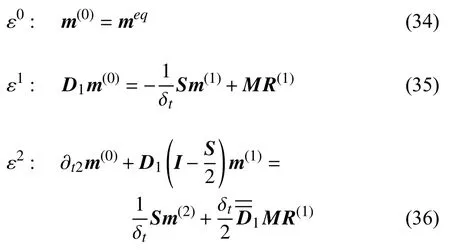
其中

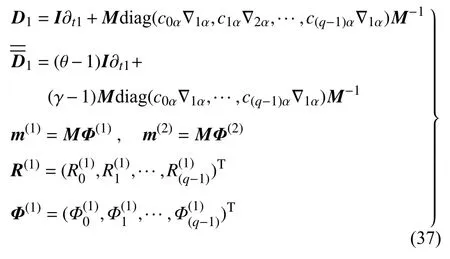
参考黄荣宗等[34]的MRT 多块对流扩散LB格式推导,结合对矩空间分布函数与非平衡态矩的关系,有下式成立

式中m(0)即为平衡态分布矩,满足

将式(39)代入式(36),可得

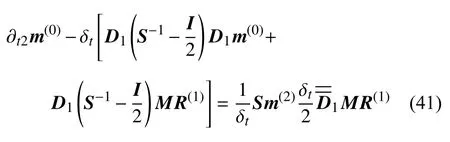
分析上式,为满足不同网格之间信息交换的网格无关性,应满足

结合式(35)和式(38),可得

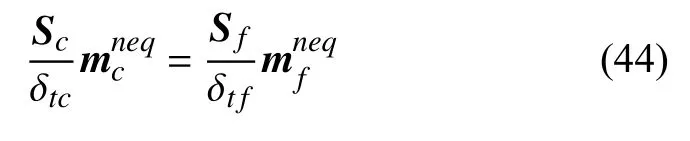
又因为碰撞后的分布函数矩可以写为非平衡态格式

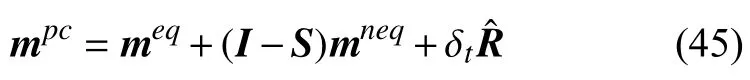
式(47)中,在粗网格到细网格的边界信息传递过程中,粗网格边界的值要先经过一次空间插值,获得对应细网格所有节点的值,然后还要对矩空间分布函数实施时间插值以获得信息交换的.

2.4 网格界面插值格式选取

由于LBM 具有时间和空间二阶精度,因此网格界面需要选取更高精度的插值格式.本文中时间插值选用三点拉格朗日插值,空间插值采用自然边界条件的三次样条插值[35]

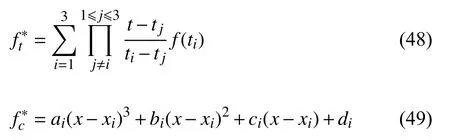
其中,式(48)代表三点拉格朗日插值,式(49)为三次样条插值,系数选取参见式(50),σi代表二阶导数,具体的实施可查阅相关参考文献[35]

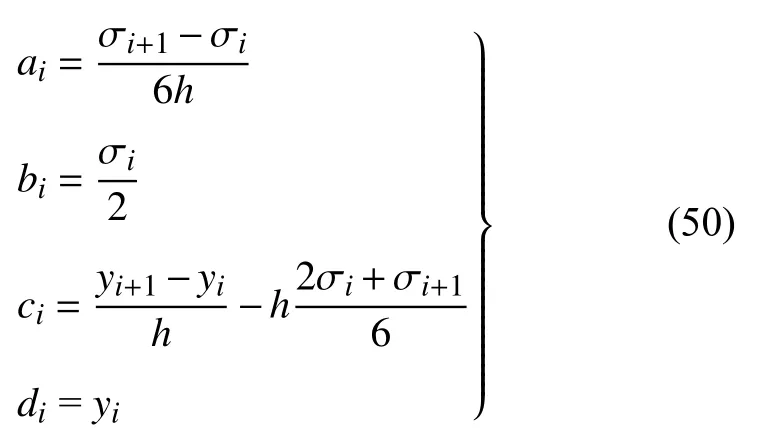
以二倍加密系数为例,图5 给出了多块网格算法实施过程.

图5 多块网格 LBM 算法求解步骤Fig.5 Solving steps of multi blocks LBM

3 离子交换表面的电对流模拟

本节采用前文提出的多块LB 方法对离子交换表面电对流进行数值模拟.考虑对称二元电解质氯化钾(KCl)溶液为工质,并假设正负离子扩散系数相同,其他所选用的物性参数如表1 所示.

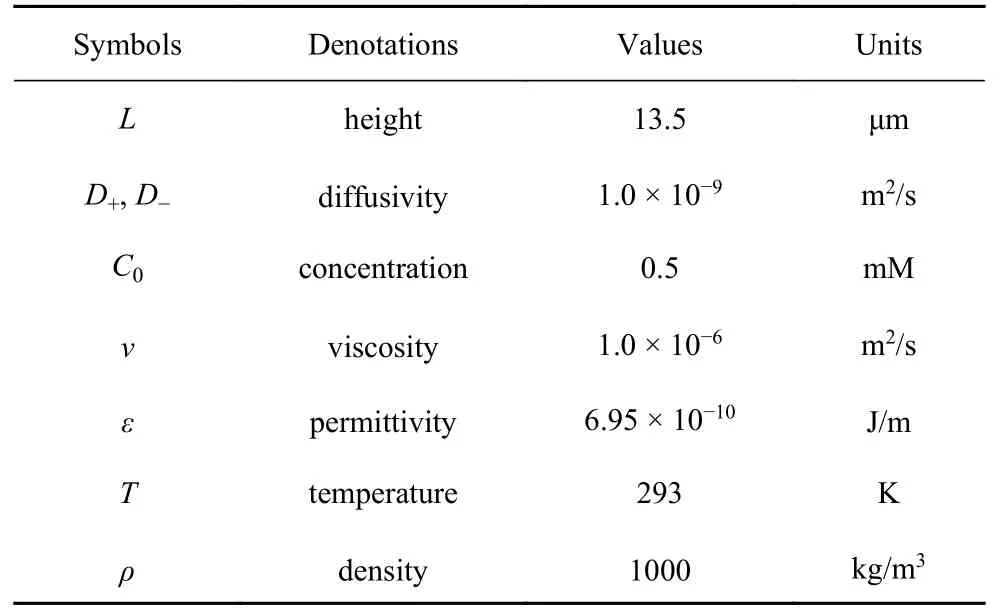
表1 模拟选用物性参数Table 1 Physical properties used in simulations

根据物性表1 计算得到,饱和限制电流密度为Ilim=7.15m2/s,德拜长度 λD=13.48 nm,规定特征电压(热电压) φ0=kBT/(ze)= 25.25 mV.

图6 给出了不同网格加密级数下的网格配置(1:2:2 与1:2:4)示意图以及部分相应的模拟结果,其中最粗的网格密度为200.从流线可以看出模拟结果在不同网格的加密处有很好的连续性,说明该局部加密算法的可靠性.此外,分别对格子密度为160,200,250 (均代表最粗网格的格子密度,细网格部分按比例增加,下同),模拟结果均有很好的一致性.下文的计算结果均采用200 个格子(以粗网格计)计算得到,计算域设为1:1.

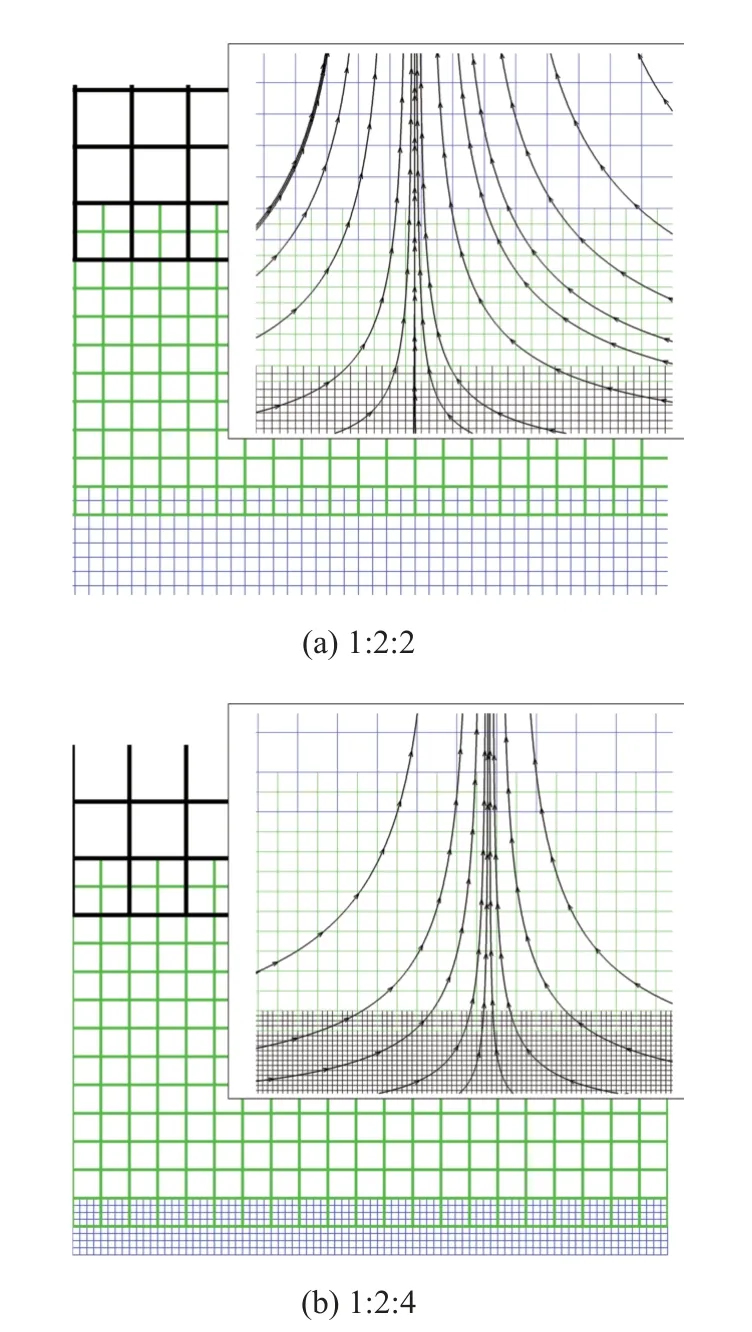
图6 多块网格排布示意图及计算流线分布Fig.6 Schematics of multi blocks grids arrangement

3.1 电流随电压的变化

图7 给出了随着电压增加,溶液中电流密度随电压的演化特性曲线.可以看出电流密度随电压的变化趋势表现为先增长后趋于饱和,在电压到达一个阈值后继续增加.电压低于 7φ0时,随着电压的增加,通过系统的电流密度迅速增大;电压大于 7φ0时,电压继续增大,电流密度的增长几乎停滞,趋于饱和;当电压达到 21φ0时,电流密度继续增大,表现为非线性增长趋势.

图7 离子交换表面的电流-电压(I-V)特性曲线,蓝色线条为模拟结果,橘色虚线为根据Yariv 的渐近分析获得的理论解,红色虚线为人为抑制流动所获得的数值解Fig.7 The relationship of voltage-current near the ions selective surface.The blue line represent the numreical result,the orange dotted line is the analytical solution form Yariv's asymptotic analysis,the red dashed line is the numerical solution obtained by suppressing the flow artificially

图7 中点划线表示通过人工抑制流动发生从而得到的没有对流输运的电流曲线,虚线代表Yariv等[32]通过渐近展开推导得到的一维情况下的电流解析解.一方面,本文的数值结果在有流动和无流动的情况下都与文献[32]的理论解吻合得很好,定量证明了当前多块LB 模型的正确性;另一方面,后期电流的再次增大也定性验证了流动对过饱和电流的贡献.

3.2 流动未发生时的浓差极化现象

图8(a)给出了没有流动发生时系统的正负离子浓度分布特性曲线,其中 25φ0的模拟结果是在人为抑制流动的状态下计算得到的.在离子交换表面附近,离子浓度迅速衰减,表现为双电层扩散分布的特性.扩散层的离子浓度呈线性分布,此时离子输运由扩散机制主导.

图8(b)给出了离子浓度C=C+-C-的分布特性.电压达到饱和限制区域之后,离子交换表面附近的负离子被耗尽,形成了ESC 层.ESC 层积累的净电荷量远大于EDL 内部,而外部的扩散层仍保持电中性.从图8(b)中还可以看出,在扩散层与扩展空间电荷层之间还存在一个净离子浓度增大的过渡层TL,这一模拟结果与相应的理论分析一致.

图8 流动未发生时的离子浓度分布.(a) 正负离子浓度分布,正负离子浓度只在壁面附近有所不同,仅用点来区分不同电压下的结果;(b) 净离子浓度分布Fig.8 The ions concentration distribution near the ions selective surface without convection.(a) Cations and anions concentration.The cations and anions are different near the wall while are the same in DL,so we only use markers to distinguish the results under different voltages.(b) Net charge density

3.3 不同电压下的流动发展

进一步以 20φ0下的稳态结果为模拟初始条件,增加电压,获得不同电压下的流动演化.在本文所研究的电压范围内,离子交换表面的电对流状态最终都会达到相似的稳态,但是流动随时间的演化特性会不同,下面对不同外加电压下的流动演化特性进行分析.

如图9 所示,在 22φ0的电压下,系统需要经历较长时间才能产生流动.模拟初始阶段,最大流动速度呈指数增长,由于此时的流动速度较小,不足以引起电流密度的显著变化,整个系统的离子输运仍处于扩散机制主导阶段,流动形态在初始阶段即为对称的涡结构.随着流动增强,流动对离子输运的贡献逐渐显现,电流也随之增大.流动强度达到峰值之后稍有回落,进入电流减小的过渡阶段.

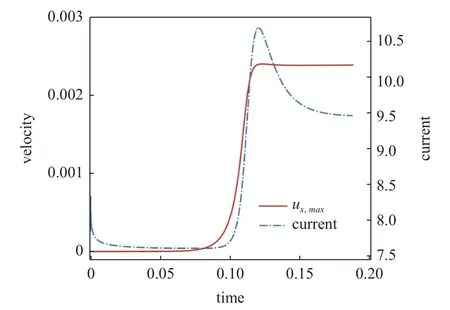
图9 V=22φ0 最大横向速度与电流密度的演化曲线Fig.9 The maximum lateral velocity and current density development curve when V=22φ0

图10 给出了系统到达稳态之后的流动形态和离子浓度分布,流场朝内侧聚集,离子浓度呈驼峰状分布.在离子浓度耗尽程度较大的区域,电解质溶液向上流动,携带离子远离表面,表现为对离子输运的加强,并在两侧汇集到离子选择性表面,抵消了一部分电迁移作用,表现为局部电流密度的减弱.由于流动强化离子输运作用更强,离子输运效率随之增大,最终导致电流增大.

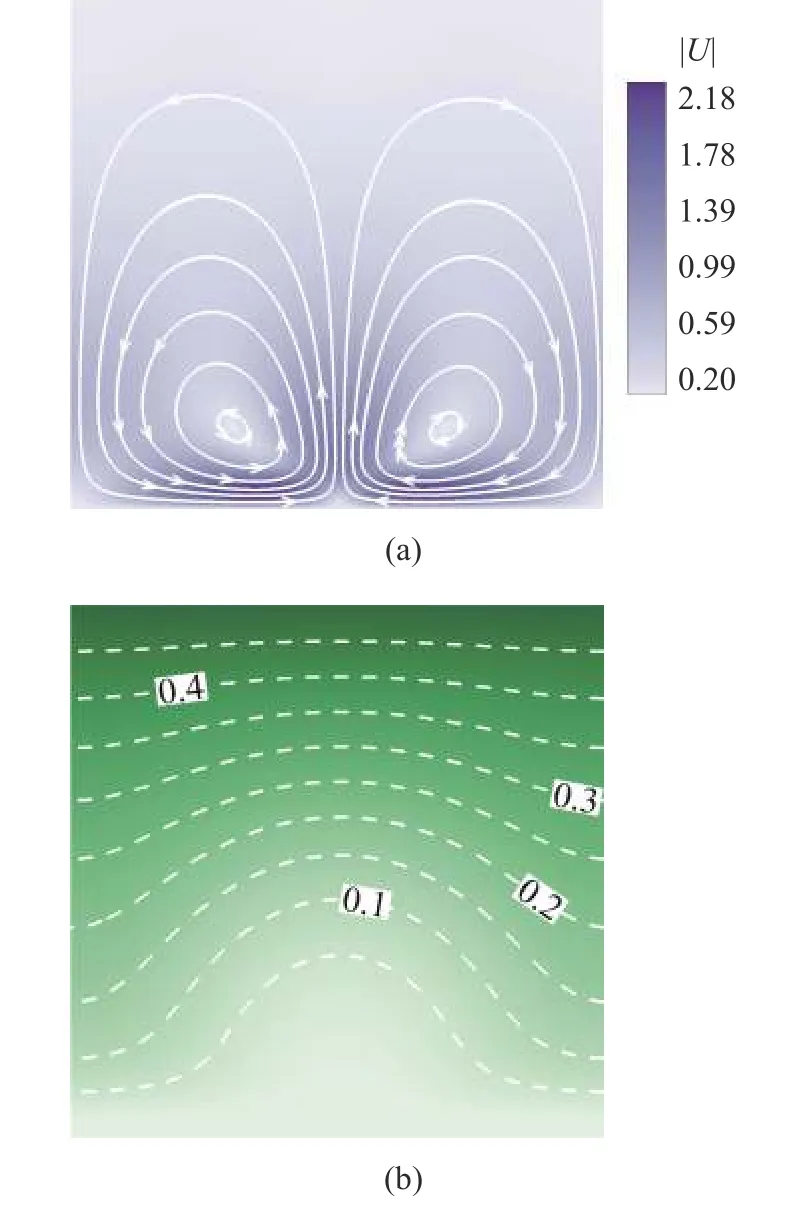
图10 V=22φ0 稳态流动强度和和阴离子浓度分布.(a) 流场分布,(b) 阴离子浓度Fig.10 Contour of (a) fluid velocity and (b) anions concentration on steady state with V=22φ0

当电压增大为 26φ0时,流动随时间的演化表现出不同的特性.如图11 所示,相比于V=22φ0,这一电压下流动发生了两次明显的变化,最终达到稳态.较强的电场力在流动开始阶段就导致了明显的扰动,流动在初始阶段表现为两对小涡,强度随着扰动的积累而增大,最终影响离子浓度分布.如图12(a)和图12(b)所示,此时离子耗尽区的浓度分布与流动形态一致.这种小涡流动并不稳定,会随着时间的演化逐渐过渡到大涡.如图12(c)和图12(d)所示,右侧的两个涡逐渐增大,合并了左侧的小涡,相应的离子浓度分布也随流动而改变,对流涡对离子输运的影响继续增大.

图11 V=26φ0 最大横向速度与电流密度的演化曲线Fig.11 The maximum lateral velocity and current density development curve when V=26φ0

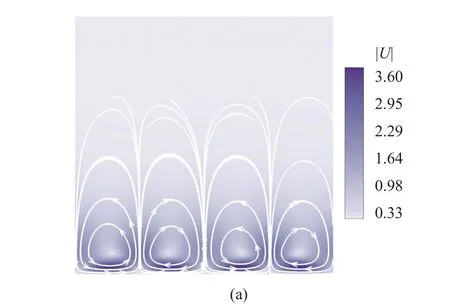
图12 V=26φ0 不同时刻的流动和离子浓度分布,(a),(b)对应于图11 中0.02 s,(c),(d)对应于0.03 sFig.12 Contour of velocity and anions concentration at different evolution time when V=26φ0,the subfigures (a),(b) corresponds to 0.02 s and (c),(d) corresponds to 0.03 s in Fig.11

图12 V=26φ0 不同时刻的流动和离子浓度分布,(a),(b)对应于图11 中0.02 s,(c),(d)对应于0.03 s (续)Fig.12 Contour of velocity and anions concentration at different evolution time when V=26φ0,the subfigures (a),(b) corresponds to 0.02 s and (c),(d) corresponds to 0.03 s in Fig.11 (continued)

图11 中,电流密度在流动发生之后也出现了两次转变,分别对应于小涡流动增强离子输运、小涡转变为大涡流动.两种流态的最大速度并没有太大差距,但是大涡状态下的离子输运效率更强.该电压下的最终的稳态流动与图10 类似,但流动强度明显提高.

4 结论

针对离子交换表面的电对流问题,本文首先提出了一种多块LB 电流体求解算法.该方法采用多松弛格式计算电场分布,提高了程序的稳定性;用多块网格局部加密格式,较好地解决了计算资源在模拟区域不同范围内的分配问题,可有效处理离子交换表面边界离子分布的强烈变化.随后,利用新发展的模型对离子交换表面的浓差极化和流动现象进行了模拟,分析了不同电压下的流动随时间的演化特性.模拟结果与渐近理论解吻合良好,捕捉到了不同电压下的电流特性曲线.在相对低的电压下,流动倾向于直接形成大涡,而更大的电压则会在初期就激发小涡流动,并逐渐合并为大涡流动结构.相比于小涡,大涡流动具有更高的离子输运效率.

本文提出的多块LB 电流体求解格式给出了三个对应于不同宏观方程的介观分布函数在不同精细度网格界面的信息交换格式,也可用于数值求解电荷单极注入电对流、电渗流等其他电场与流动的耦合问题.该多块局部LB 算法具有良好的可拓展性,后续可在此基础上发展自适应网格的求解算法[34],以适应更加灵活的电流体动力学问题的求解.