波形钢腹板结构参数变化对其稳定性的影响
茹超 张运波 欧阳稳 李运生
1.石家庄铁道大学土木工程学院,石家庄 050043;2.北京特希达交通基础设施顾问有限公司,北京 100011
波形钢腹板PC(Prestressed Continuous)组合箱梁是由混凝土顶底板、波形钢腹板、体内和体外预应力组成的一种新型桥梁结构,该种桥型具有受力合理、施工方便、经济效益显著等特点,逐渐应用在工程领域。在施工过程中,顶底板湿重及临时施工荷载以压力的形式施加在钢腹板上翼缘,很可能导致波形钢腹板产生几何缺陷。成桥后在运营期间承受汽车荷载、人群荷载等,易发生失稳现象,故波形钢腹板安全问题主要是稳定性问题,而发生波形钢腹板稳定性问题是因为发生了屈曲破坏。研究波形钢腹板剪切屈曲模式发现,其屈曲模态主要有合成屈曲、局部屈曲以及整体屈曲。
文献[1-2]最早开始对波形钢腹板的剪切屈曲行为进行研究,此后众多国内外学者提出了局部屈曲和整体屈曲的计算公式。文献[3-4]提出了关于波形钢腹板合成屈曲的计算公式。文献[5-6]利用有限元软件精确分析并研究了波形钢腹板剪切屈曲模式以及影响因素。文献[7-8]通过大量数值计算和参数分析,提出波形钢腹板弹性剪切屈曲强度的简化计算公式和抗剪强度曲线。文献[9]研究了波形钢腹板箱梁桥的抗剪受力性能。
已有文献鲜有研究波形钢腹板稳定性随参数变化的规律。本文以国内应用广泛的1600型波形钢腹板为对象,研究波形钢腹板PC组合箱梁桥成桥后,在汽车荷载、人群荷载等荷载情况下的剪切屈曲行为,以及发生局部屈曲、整体屈曲的高度和厚度范围。
1 ANSYS有限元模型建立
根据波形钢腹板不同高度和厚度选取shell181单元建立有限元模型。增加模型长度可以弱化左右两端边界约束的影响,故建模时取10个波段,总长度为16 m。考虑成桥后波形钢腹板屈曲行为,波形钢腹板PC组合箱梁桥顶底板均已浇筑,有限元模拟时汽车荷载等按照均布荷载施加在波形钢腹板上边缘,同时约束波形钢腹板各个边缘上相应的自由度。
特征值屈曲分析时将单位1的均布荷载施加到波形钢腹板的上边缘[10],则特征值屈曲分析得到的屈曲荷载系数即为屈曲极限荷载。
非线性分析的外荷载取特征值屈曲极限荷载的1.2倍,并将其施加在波形钢腹板的上边缘。输出足够多的子步数结果,从而方便后处理中得到荷载-位移曲线[11]。
非线性屈曲分析时需要考虑波形钢腹板的初始缺陷。钢腹板运输过程中发生变形、现场构建安装不精确等因素都会产生初始缺陷。波形钢腹板的初始缺陷包括几何缺陷和材料缺陷。材料缺陷主要指钢腹板的厚度缺陷,波形钢腹板厚度按照符合标准要求考虑,故只考虑几何缺陷。此外,需要定义钢腹板的本构关系。钢材采用Q345D,ANSYS材料属性输入泊松比0.3,弹性模量2.1×105MPa,屈服准则采用Von Mises,即分别为钢的剪切屈曲强度和抗拉屈服强度。钢材本构关系曲线见图1。
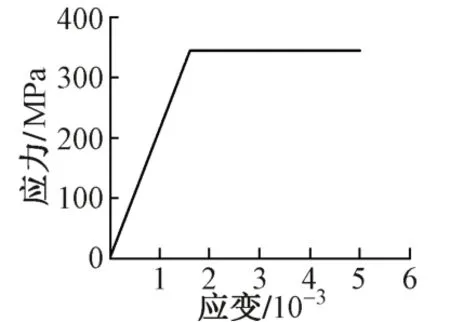
图1 钢材本构关系
采用一致缺陷模态法模拟钢材的初始缺陷。参考各国规范,初始缺陷幅值取波形钢腹板短边长度的1∕300作为初始位移幅值[12]。非线性分析时先根据一阶屈曲模态计入初始几何缺陷,更新计算模型(即将一阶屈曲模态的位移乘以波形钢腹板短边长度的1∕300作为初始缺陷)[5]。考虑几何大变形效应,采用弧长法对非线性求解并进行迭代控制。由于大变形分析时结构刚度和变形相互影响,通过弧长法调整迭代次数可以得到一个高精度的解。
2 波形钢腹板尺寸拟定
由于国内关于波形钢腹板尺寸通用标准较少,因此需要精准确定波形钢腹板尺寸划分范围,指导波形钢腹板的设计和施工。JT∕T 748—2010《组合结构桥梁用波形钢腹板》中推荐了三种类型的波形钢腹板形状尺寸,分别为1000型、1200型和1600型,其几何尺寸和几何形状分别见表1和图2。我国采用最多的是1600型钢腹板[13]。
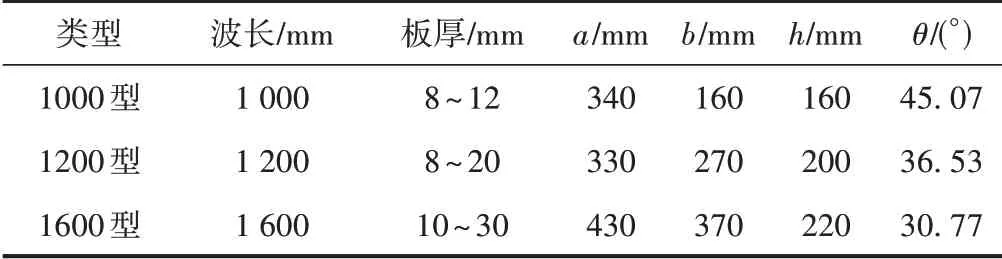
表1 常用波形钢腹板的几何尺寸

图2 波形钢腹板的几何形状
3 特征值屈曲分析
特征值屈曲分析不需要考虑几何非线性、材料非线性以及初始几何缺陷。对于基本结构配置,结构特征值是根据约束条件和荷载条件计算出来的,然后推导出屈曲荷载,每一荷载都与一个屈曲模态形状相关。由于特征值屈曲分析结果精度较低,因此只用于分析波形钢腹板屈曲模态形状。
分析1600型波形钢腹板不同厚度和高度对其屈曲极限荷载和一阶屈曲模态的影响。参数化分析过程中采用控制变量法,各个计算模型荷载、边界条件、波形钢腹板长度均相同。分析不同厚度影响时,其他各项参数(如高度、波长、折角等)均相同;分析不同高度影响时,其他各项参数均相同。波形钢腹板厚度t取10~30 mm,波形钢腹板高度H取2~10 m。
波形钢腹板一阶屈曲模态见图3。其中,F为屈曲极限荷载;其他数据为波形钢腹板相对位移。
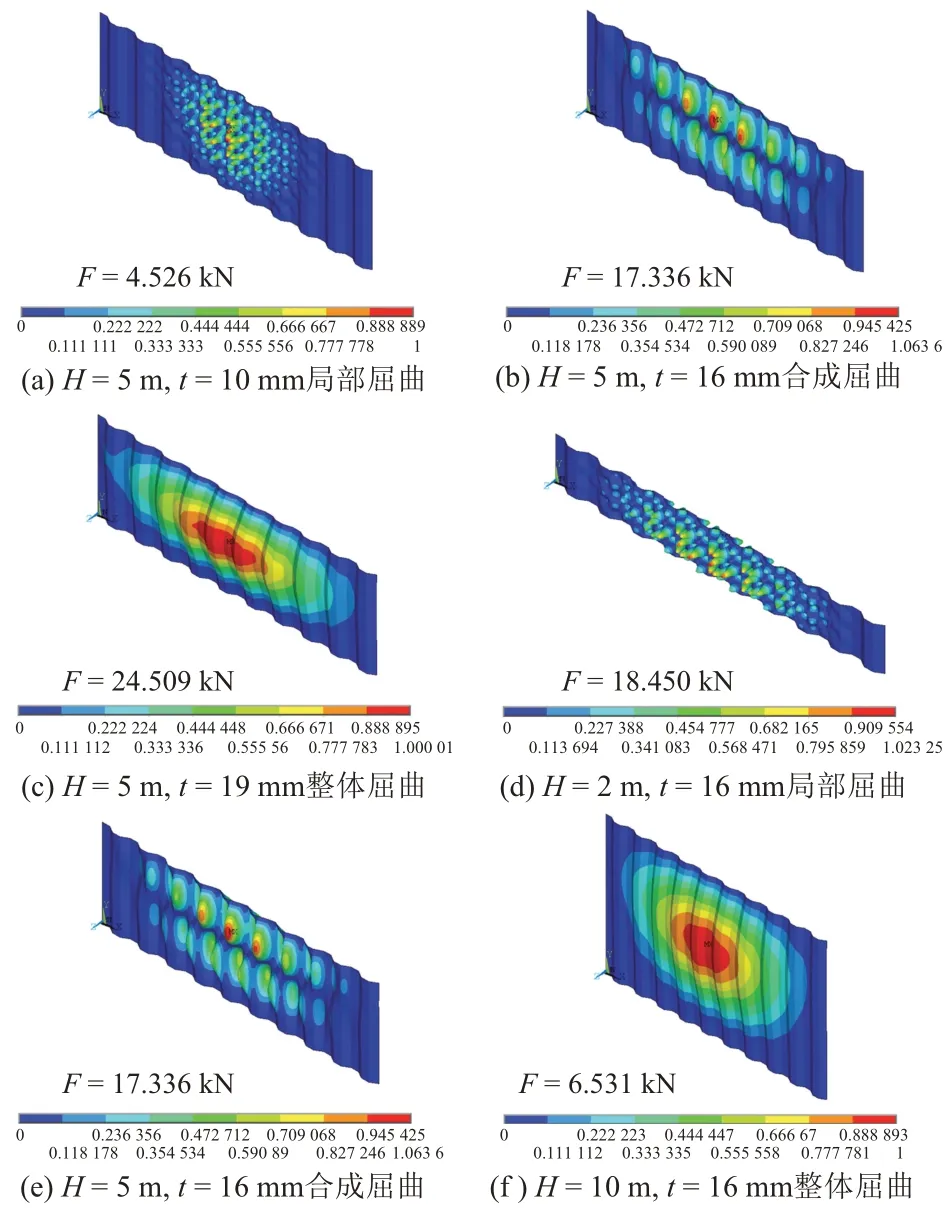
图3 波形钢腹板一阶屈曲模态
由图3可知:①改变波形钢腹板的高度和厚度,其屈曲模态共有三种,分别为发生单个板条内的局部屈曲、单个波段内跨越数个板条的合成屈曲、发生跨越数个波段的整体屈曲。②随着波形钢腹板厚度或高度的增加,屈曲模态从单个板条内的局部屈曲向跨越数个波段的整体屈曲发展。③随着波形钢腹板厚度(高度)的增加,屈曲极限荷载逐渐增大(减小)。
1600型波形钢腹板不同屈曲模态的高度和厚度范围见表2。可知:波形钢腹板高度较高时,在常用厚度范围内屈曲模态均为整体屈曲;波形钢腹板高度较低时,在常用厚度范围内不发生整体屈曲。
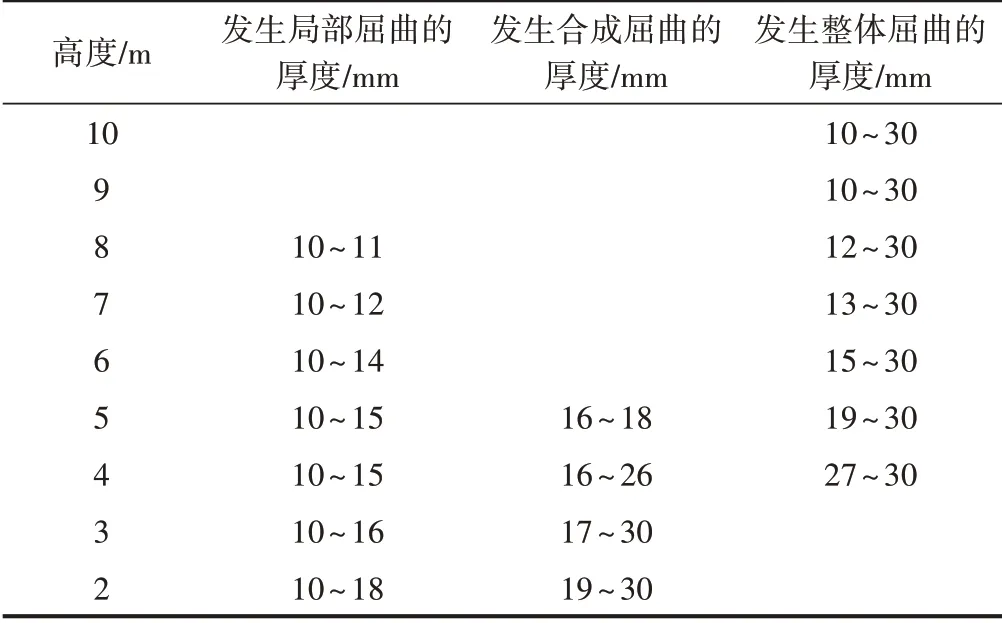
表2 1600型波形钢腹板不同屈曲模态高度和厚度范围
4 非线性屈曲分析
非线性屈曲分析是一种精度较高的静力学屈曲分析方法,该种分析方法需要考虑材料和几何非线性、荷载扰动、几何缺陷和间隙。非线性屈曲分析的目的是得到真实的结构极限荷载,而不是理论解(线性屈曲分析的第一阶屈曲模态对应的荷载)。非线性屈曲比特征值屈曲计算的结果更精确,且非线性屈曲分析能够比较好地得到构件屈曲后特性。
非线性屈曲分析时首先进行线性屈曲分析得到临界荷载,然后将临界荷载的1.2倍作为非线性屈曲分析的外荷载。
4.1 不同腹板厚度非线性屈曲
由特征值屈曲分析可知,t=12、13、14、15 mm属于局部屈曲,t=20、25 mm属于合成屈曲,t=30 mm属于整体屈曲。在同一腹板高度(H=5 m)下对不同厚度波形钢腹板进行非线性屈曲分析,计算结果见图4。纵坐标为施加外荷载的百分比(即荷载占1.2倍临界荷载的百分比),横坐标为钢腹板z向位移(沿波形钢腹板板厚方向)。可知,局部屈曲发生屈曲后的行为与整体屈曲有明显区别,局部屈曲的荷载-位移曲线在越过极值点后迅速降低,板厚越小曲线下降越快,塑性发展能力较差。整体屈曲与此规律相反,屈服后承载力稍有增加,波腹板塑性变形开始快速发展。

图4 不同腹板厚度下波形钢腹板荷载-位移曲线
屈曲极限荷载随腹板厚度变化曲线见图5。可知,随着波形钢腹板厚度的增加,屈曲极限荷载大致成正比例线性增加,且腹板高度越小,曲线斜率越大。
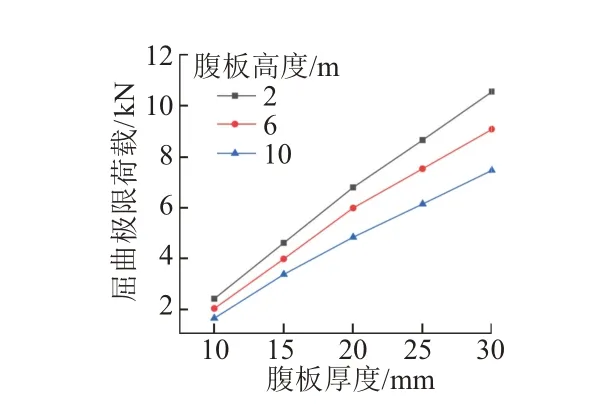
图5 屈曲极限荷载随腹板厚度变化曲线
4.2 不同腹板高度非线性屈曲
由特征值屈曲分析可知,H=2~5 m属于合成屈曲,H=6~10 m属于整体屈曲。在同一腹板厚度(t=20 mm)下对不同腹板高度波形钢腹板进行非线性屈曲分析,计算结果见图6。可知:不同腹板高度和厚度下的荷载-位移曲线变化规律相似;随着整体屈曲向局部屈曲过渡,屈曲后荷载-位移曲线下降越来越缓。
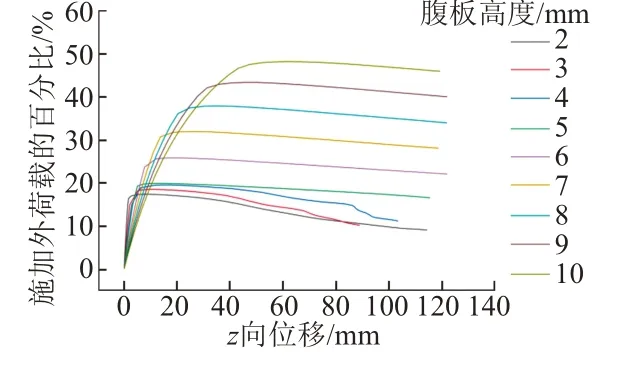
图6 不同腹板高度下波形钢腹板荷载-位移曲线
屈曲极限荷载随腹板高度变化曲线见图7。可知,增加波形钢腹板高度时,屈曲极限荷载大致成正比例线性减小,且腹板厚度越大,曲线斜率越大。
综上所述,设计波形钢腹板尺寸时建议综合考虑厚度和高度,当梁高变化时要适当改变其厚度,避免整个桥梁的波形钢腹板屈曲极限荷载相差过大。
5 结论与建议
1)随着波形钢腹板厚度和高度的增加,其一阶屈曲模态由局部屈曲逐渐发展为整体屈曲。
2)随着腹板厚度的增加屈曲极限荷载大致成正比例线性增加,且腹板高度越低,屈曲极限荷载增加得越快;随着波形钢腹板高度的增加,屈曲极限荷载大致成正比例线性减小,且腹板厚度越大,屈曲极限荷载减小得越快。
3)对于不同厚度的波形钢腹板,局部屈曲的荷载-位移曲线在屈服后下降速度较快,整体屈曲的荷载位移曲线在屈服后下降速度较慢。
4)对于不同高度的波形钢腹板,局部屈曲的荷载-位移曲线在发生屈服后下降速度较快,而整体屈曲的荷载-位移曲线在屈服后下降速度较慢。
本文非线性分析得到的极限屈曲荷载小于线性屈曲分析得到的极限屈曲荷载,线性分析得到的极限屈曲荷载是偏危险的,故对结构进行屈曲分析时建议先做非线性屈曲分析,如果与线性分析结果相差很小,则不必考虑几何非线性问题,否则必须进行非线性分析。

