基于水平抗推刚度的长联刚构桥合理桥墩形式研究

冯林军， 刘梦琦， 余茂峰， 郭斌强

(1.浙江交投交通建设管理有限公司， 杭州 310000； 2.浙江数智交院科技股份有限公司， 杭州 310000)

随着我国经济的快速发展，桥梁建设的使用需求及技术标准不断提高，桥梁设计理念更加注重桥梁行车的舒适性、耐久性、施工便利性及全寿命周期的经济性。常规桥梁结构体系一般采用简支或先简支后连续结构，2种常规桥梁结构均需设置支座和伸缩缝且需定期维修养护和更换。长联刚构桥梁可大量减少伸缩缝和支座使用，提高结构的延性和抗震性能，改善行车舒适性[1-2]。然而连续刚构桥梁的长联化会使得桥梁纵桥向水平力(汽车制动力、风荷载)和温度力(升温、降温、收缩)的影响大幅度增大，其中温度力的作用主要由外侧桥墩承担，水平力会根据下部结构水平抗推刚度比例进行分配，致使外侧桥墩墩顶水平位移通常较大。通过合理设置各桥墩水平抗推刚度，不仅可增加桥墩墩顶的容许位移，改善结构的内力分配，还可减小处于不利位置的墩身受力，降低结构附加内力对墩顶处主梁的影响[3]。

1 结构分析

1.1 分析模型

(a) 单肢墩(b) 双肢墩

在连续刚构体系中，假定上部结构主梁在墩梁连接处的刚度远大于桥墩的刚度，桥墩墩顶水平位移和转角位移均受到主梁的约束，单肢墩和双肢墩的计算分析模型可看作桥墩顶、底分别与主梁和基础固结在一起。对于单肢墩，在纵向水平力的作用下，墩顶发生纵向水平位移，墩顶处不产生转角，计算分析模型如图2(a)所示。对于双肢墩，假定双肢墩之间的主梁相对于桥墩为完全刚性，若不考虑桥墩两肢之间由于混凝土材料特性所产生的轴向变形差异，则墩顶仅发生纵向水平位移，主梁不产生转角，计算分析模型如图2(b)所示； 如果考虑双肢墩的两肢桥墩之间由于混凝土材料特性发生不同的轴向变形，墩顶除了产生纵向水平位移，同时主梁会根据两肢不同的轴向变形量产生一定程度的转角[5]，计算分析模型如图2(c)所示。图2中，P为纵桥向荷载，E为桥墩材料弹性模量，A为单肢墩和双肢墩横截面面积，I为单肢墩和双肢墩惯性矩，L为桥墩高度。

(a) 单肢墩

1.2 墩顶水平位移和抗推刚度

(1)

单肢实心墩的墩顶水平抗推刚度为：

(2)

当图1(a)为单肢空心墩，将单肢空心墩的截面惯性矩大小代入式(1)，可得墩顶水平位移为[6]：

(3)

根据式(2)可得单肢空心墩的墩顶水平抗推刚度为：

(4)

对于双肢墩，在不考虑桥墩两肢之间的轴向变形差异的理想情况下，主梁不发生倾转，墩顶仅发生纵向水平位移，如图2(b)所示，根据分析计算可得双肢墩的墩顶水平位移为：

(5)

不考虑桥墩两肢之间的轴向变形差异的双肢墩墩顶水平抗推刚度为：

(6)

但在实际情况中，由于混凝土材料特性，桥墩两肢之间会发生不同程度的轴向变形，主梁也会发生一定程度的倾转，此时双肢墩墩顶既有纵向水平位移又有一定的转角位移，如图2(c)所示，按结构力学方法计算可得墩顶水平位移为[7-8]：

(7)

当考虑桥墩两肢之间会发生不同程度的轴向变形时，双肢墩墩顶水平抗推刚度为：

(8)

(9)

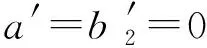
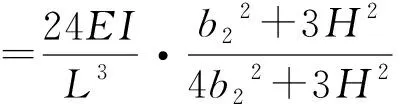
(10)

(11)

(12)

1.3 抗推刚度对比分析

(13)

图3 水平抗推刚度比值与H/b的关系

从图3可以看出，在双肢墩与单肢墩实心截面尺寸相同的情况下，双肢墩比单肢墩的水平抗推刚度小[9-10]。当03时，双肢实心墩水平抗推刚度大小已超过了相同实心截面尺寸单肢实心墩水平抗推刚度的90%。为保证双肢墩的柔性，有效改善墩身之间的内力分配，建议双肢间距H与双肢墩单肢的纵向宽度b2的比值不大于3[11]。

2 基于水平抗推刚度的桥墩设置合理性研究

2.1 桥墩影响因素

长联刚构桥中，桥墩的墩顶水平位移主要来自上部结构所承担的纵桥向水平力和温度力的作用[12]。水平力包括汽车制动力和风荷载，其计算模型如图4所示。在水平力作用下，每个桥墩的墩顶水平位移Δs均相等，每个桥墩所分配的弯矩为Msi=Δs·f(Ki)，其中f(Ki)为含桥墩水平抗推刚度K的函数式。经分析研究，每个桥墩的弯矩Msi与f(Ki)中的水平抗推刚度Ki成正比关系，桥墩水平抗推刚度越大，桥墩所分配的弯矩也会越大。

(a) 位移分布

温度力包括升温、降温和收缩作用，其计算模型如图5所示。在温度力作用下，每个桥墩的墩顶水平位移Δwi与桥墩距桥梁中心不动点的距离Li有关。假设上部结构由于温度变化引起的应变为ε，应变ε在桥梁各个位置大小相同，每个桥墩在温度力作用下的墩顶水平位移为Δwi=Li·ε，每个桥墩所分配的弯矩为Mwi=Δwi·f(Ki)。

(a) 位移分布

2.2 桥墩合理性设置

在长联刚构桥梁中，每个桥墩的纵桥向弯矩为Mi=Msi+Mwi=Δsi·f(Ki)+Δwi·f(Ki)。与水平力和温度力相比，支座沉降、自重等因素所引起的桥墩弯矩大小暂且可忽略。对于连续刚构桥梁，如果每个桥墩保持水平抗推刚度相等，水平力作用所引起的每个桥墩的弯矩大小相等。但由于温度力的特点，越远离桥梁不动点(即Li越大)，桥墩所分配的弯矩最大，越靠近桥梁中心不动点，弯矩越小。这种内力叠加会使得外侧桥墩承担过大的弯矩而难以满足设计验算要求。因此，为合理改善结构内力分配，应使得长联刚构桥梁中任意2个桥墩的弯矩Mi和Mj之比保持在相似水平[13-14]，即

(14)

由此可得长联刚构桥梁中任意2个桥墩的水平抗推刚度Ki和Kj之比为：

(15)

2.3 工程应用

单位：m

从图7可以推出如表1所示的数值对应关系，当桥墩距离不动点达到40 m时，其桥墩墩顶水平抗推刚度需等于不动点处的桥墩水平抗推刚度的40%；当桥墩距离不动点达到70 m时，其桥墩墩顶水平抗推刚度需为不动点处桥墩水平抗推刚度的25%；不动点处墩顶桥墩水平抗推刚度较大，可设置为单肢墩，并将该墩的水平抗推刚度大小作为基准水平抗推刚度。对于远离不动点的桥墩可通过设置双肢墩来减小墩顶水平抗推刚度，若使墩顶抗推刚度减小40%，在单肢墩和双肢墩尺寸相同的情况下，

图7 水平抗推刚度比值与桥墩距离不动点Li的关系

则H/b2<0.5；但若使墩顶抗推刚度减小25%，在单肢墩和双肢墩尺寸相同的情况下，则H/b2=0，所以当桥墩距离不动点超过70 m时，还需进一步调整双肢墩的尺寸来减小水平抗推刚度。

表1 桥墩位置与桥墩尺寸的数值对应关系

图6所示的(7×30)m浙江某城市长联刚构高架桥0#和7#边墩采用支座连接并释放纵桥向位移约束，中间3#至4#桥墩桥墩距离不动点15 m，拟以3#和4#桥墩水平抗推刚度为基准水平抗推刚度；2#～5#桥墩距离不动点45 m，根据图7可得其水平抗推刚度需为3#和4#桥墩水平抗推刚度的50%；1#和6#次边墩距离不动点75 m，根据图7可得其水平抗推刚度约需为3#和4#桥墩水平抗推刚度的38%。根据水平抗推刚度的计算，2#～5#墩采用单肢实心墩，各个桥墩的尺寸根据水平抗推刚度的变化要求进行设计。同时由于1#和6#次边墩刚度需大幅度减小，采用双肢薄壁实心墩，按照水平抗推刚度的变化要求进行尺寸设计，结果如表2所示。

采用Midas对实桥建模且进行有限元分析，并按照墩高一致的情况计算出1#～6#桥墩由水平力和温度力引起的弯矩大小，结果如表3所示。

表2 各个位置的桥墩水平抗推刚度与合理设置形式

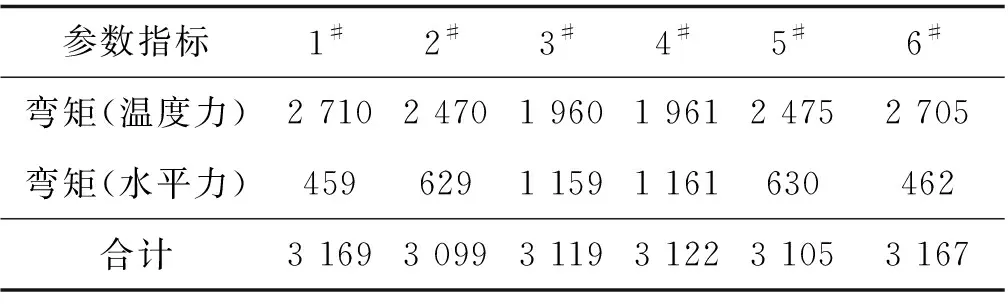
表3 各因素作用下弯矩大小 kN·m

从表3可以看出，在水平力和温度力共同作用下，每个桥墩的弯矩分配基本一致，长联刚构桥梁桥墩内力分配合理，结构的内力分配得到改善，有效减小了最不利墩身的内力。

3 结束语

1) 相同尺寸的双肢实心墩比单肢实心墩水平抗推刚度小，其比例关系与双肢间距和双肢墩的单肢纵桥向宽度的比值有关，建议双肢间距与宽度比值不大于3。

2) 桥墩的墩顶水平位移受水平力和温度力的影响，各个位置的桥墩水平抗推刚度大小的设计与其距不动点的距离有关并成反比关系。

3) 在设计长联刚构桥梁时，可先定量水平力所引起的位移与温度力所引起的应变的比值，然后可以得出各个桥墩水平抗推刚度与桥梁水平抗推刚度基准值的比例关系，并以此为依据进行下部各个桥墩形式的设计。

4) 双肢墩的造价一般较单肢墩高，如果通过改变单肢墩的尺寸可以满足设计要求，设计时建议尽量选用单肢墩。

5) 如果桥梁所处位置的地势变化较大，桥墩墩高的影响也应作为重要设计影响因素进行考虑。