基于单目视觉的钻杆位姿识别技术研究

马斌，彭光宇

(中煤科工西安研究院(集团)有限公司，陕西 西安 710077)

2015 年原国家安监总局印发了关于开展《“机械化换人、自动化减人”科技强安专项行动》的通知；2016 年中华人民共和国国家发展和改革委员会与国家能源局印发了《能源技术革命创新行动计划(2016-2030 年)》的通知；2020 年国家能源局等八部委联合发布了《关于加快煤矿智能化发展的指导意见》。这些重要的通知与意见均将煤矿井下设备的自动化、智能化列为重点建设内容之一[1-3]。为响应国家号召，提高钻机钻进效率，降低工人劳动强度，实现钻杆装卸自动化，煤矿相关企业、科研院所均开展了钻杆自动装卸技术的相关研究[4-6]。

姚亚峰等[7]设计了一款煤矿坑道钻机自动加卸钻杆装置，利用摆动油缸实现机械手定位，再和转轮式杆仓相互配合完成钻杆的自动装卸；王清峰等[8]设计了基于路径规划的钻杆自动输送系统，通过主机械手、副机械手和转运器的相互协作，实现钻杆自动装卸。这2 种钻杆自动系统主要依靠机械结构和接近开关实现钻杆的定点取放，在完成既定功能的同时，存在因机械磨损与累计误差等因素导致系统定位精度低的问题。同时，依靠机械结构定位的钻杆自动装卸系统自动化程度有限，智能化程度较低。如果将视觉测量技术应用到煤矿井下钻杆位姿识别中，势必可以实现钻杆定位智能识别，提高钻杆自动装卸精度和钻机装备整体的智能化水平。

视觉测量技术通常分为单目、双目和多目等形式[9-11]。单目视觉测量系统具有结构简单、成本低、实时性强等优点，在工业系统中得到了广泛的认可[12-13]。为此，提出一种基于单目视觉的钻杆位姿识别技术，利用摄像机拍摄含有合作目标的图像，结合提取到的特征信息，解算摄像机与合作目标之间的相对距离和相对姿态，并根据钻杆与合作目标之间的相对静止关系以及摄像机与机械臂的相对静止关系，推算出钻杆相对机械臂的位姿数据，引导机械手实现钻杆自动装卸。

1 总体方案

单目视觉测量分为基于合作目标和基于非合作目标两种。基于合作目标单目测量在简化特征提取难度的同时提高了特征提取的精度[14]。在此，为了准确获得钻杆的位姿信息，结合井下工作环境和钻机工作特点，选择简单方便的棋盘格作为合作目标，既简化了相机标定过程，同时也容易提取图像特征，提高测量速度。系统的整体方案如图1 所示。首先，固定摄像机，将摄像机放置在合适的地方，再对摄像机进行标定，求取摄像机的内参和外参；然后拍摄带有合作目标的图片，将图片进行灰度和滤波预处理，再对合作目标上距离世界坐标系最近的方块进行特征点提取，结合标定所得摄像机内参和外参，对钻杆进行距离测量与姿态估计，获得钻杆当前的位姿信息，将计算得到的钻杆位姿参数矩阵传输给机械臂控制器，引导机械手实现对钻杆的自动抓取。

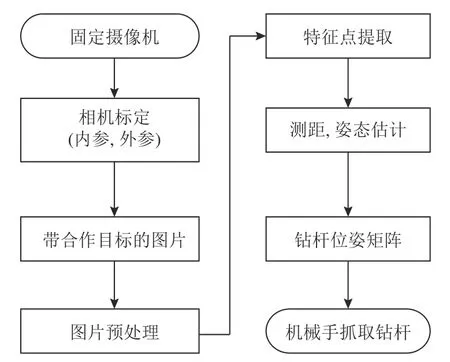
图1 系统整体方案Fig.1 Overall system scheme

2 摄像机成像模型及其标定

在视觉测量中，通常利用摄像机模型将空间中三维点与摄像机上的二维点联系起来[15]。在实际应用中，摄像机模型可用数学模型来描述，有小孔成像模型(线性模型)和非线性模型两种，其中小孔成像模型最为成熟，也应用最广泛[16]。

2.1 摄像机成像模型

小孔成像模型包括了世界坐标系、摄像机坐标系、图像坐标系和像素坐标系4 个坐标系，如图2 所示。其中P为三维空间点，p为P在图像平面投影的成像点。

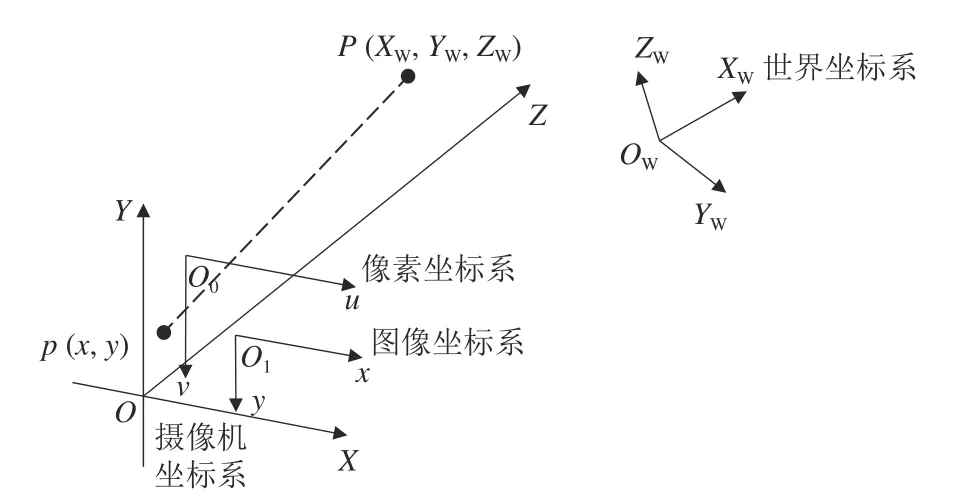
图2 小孔成像模型Fig.2 Pinhole imaging model

世界坐标系(Ow-XwYwZw) 是三维空间中的绝对坐标系，用于描述三维环境中任何一个物体的位置，一般用(Xw,Yw,Zw)表示其坐标值。摄像机安放在三维空间中，其位置信息通过世界坐标系这个基准坐标系来描述。摄像机坐标系(O-XYZ)以摄像机光心为原点，Z为主坐标轴，与摄像机光轴重合。图像坐标系(O1-xy)中O1为摄像机光轴与图像平面的交点，O-O1为摄像机的焦距，用(x,y)表示其坐标值。

像素坐标系以成像平面的左上角顶点为原点，u轴和v轴分别平行于图像坐标系的x轴和y轴，其与图像坐标系的关系如图3 所示，用(u,v)表示其坐标值。摄像机采集的图像首先形成标准电信号，再通过模数转换变换为数字图像。每幅图像可定义为M×N的数组，M行N列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素，像素坐标系就是以像素为单位的图像坐标系。而图像坐标系是用物理单位(例如：mm)表示像素在图像中的位置。像素坐标和成像坐标体现在同一图像坐标系中，成像坐标的原点O1(u0,v0)位于中心像素点上。

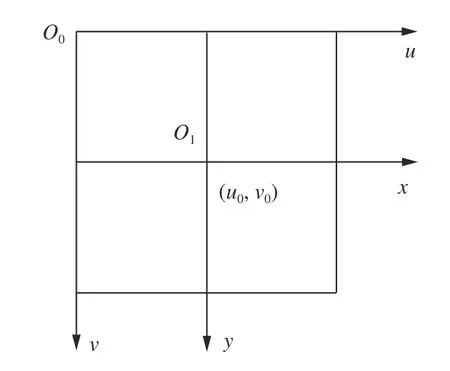
图3 像素坐标系Fig.3 Pixels coordinate systems

理想情况下O1(u0,v0)位于图像的中心处，设图像中的一个像素对应于图像坐标系在x轴的物理尺寸可表示为dx，对应于y轴方向上的物理尺寸为dy，其具体尺寸可从摄像机的参数表中获得。像素坐标与其变换关系为：

那么，图像坐标系下点p与在世界坐标系中对应点P的关系可由以下表达式描述：

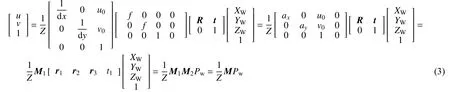
式中：f为焦距(像平面与摄影机坐标系原点的距离)；t为三维平移向量；M1为内部参数矩阵；ax、ay、u0、v0为内部参数；M2为相机的外部参数矩阵；R和t1为相机外部参数；r1、r2、r3为矩阵R中的3 个矢量；M为投影矩阵；Pw为世界坐标系中点坐标组成的矩阵。

M1中只包含由相机内部结构决定的焦距、主点坐标等参数，M2中包含由相机坐标系相对于世界坐标系的旋转矩阵和平移向量。

实际上由于相机光学系统存在加工和装配误差，相机图像平面上实际所成的像与理想成像之间会存在畸变。畸变属于成像的几何失真，是由于焦平面上不同区域对图像的放大率不同而形成的画面扭曲变形现象，这种变形的程度从画面中心至画面边缘依次递增，主要在画面边缘反映比较明显，包括径向畸变、偏心畸变和薄棱镜畸变等。实际计算过程中，引入过多的非线性参数(如离心畸变和薄棱畸变)，不仅不能提高精度，还会引起解的不稳定，一般情况下引入径向畸变就足以描述非线性畸变。

2.2 张正友标定法

相机标定是指根据摄像机图像像素位置与空间点位置之间的关系，建立摄像机模型，由已知特征点的图像坐标求解摄像机的内部参数和外部参数的过程。“张正友标定”[17]方法介于传统标定法和自标定法之间，克服了传统标定法需要高精度标定物的缺点，仅需使用打印出来的棋盘格就可以完成标定。相对于自标定而言，张正友标定法精度高，操作简单，被广泛应用于计算机视觉方面。使用大华DH-IPC-HF5221E 型号相机，其标定的主要步骤如下：

(1)准备标定图片。标定板以浮法玻璃为基质，棋盘格图案由热膨胀率较低的氧化铝材料精密加工而成，棋盘图案为12×9 棋盘格阵列，边长30 mm，角点位置精度为0.01 mm。选取18 张在不同位置、不同角度、不同姿态下拍摄的标定板图片，如图4 所示。

图4 标定照片Fig.4 Calibration photos

(2)提取每一张图片的角点信息和亚像素角点信息。角点专指标定板上的内角点，与标定板的边缘不接触。为了进一步提高标定精度，降低相机标定偏差，在初步提取的角点信息基础上进一步提取亚像素信息。如图5 所示。

(3)相机标定。获取到棋盘标定图的内角点图像坐标之后，就可对相机进行标定，计算相机内部参数和外参系数，标定中主要考虑影响较大的径向畸变，标定完后可生成相机的内部参数和畸变系数。

对相机进行3 次重复性标定，标定结果见表1。

表1 相机3 次标定结果Table 1 Three calibration results of the camera

表1 中，第一行为未考虑径向畸变时标定所得的内部参数，其余3 行为考虑径向畸变时对相机进行3 次实时标定的结果。为了减少误差，将3 次考虑畸变的标定结果求平均值得到：=2 645.79，=2 645.66，像平面中心点像素=(959.76,540.06)。

dx、dy的计算指CCD 面阵单元水平和垂直间距，已知相机的分辨率为1 920×1 080 像素，成像尺寸为4.8 mm×3.6 mm，则dx=dy=0.002 5 mm，可求出焦距f=6.61 mm。

3 单目测距及姿态评估

机器视觉中，手眼系统是指摄像机与机械手相互协调对目标进行识别和控制的系统。摄像机作为眼睛，引导机械手运动，摄像机和机械手的位置关系一般可分为2 种，一种是将摄像机(眼)固定在机械手(手)上面，眼随手移动；第二种是摄像机(眼)和机械手(手)分离，眼的位置相对于手是固定的。而手眼标定则是得到像素坐标系和机械手坐标系的坐标转化关系。

手眼标定需要将相机坐标系、世界坐标系和机械手坐标系进行关联。在本系统中，摄像机通过支架固定在机械臂底座上，在机械臂世界坐标系的固定位置处，摄像机位置如图6 所示，图中钻机主机可绕支撑点进行旋转和平移运动。世界坐标系和机械手坐标系之间的转换关系固定不变，相机坐标系和世界坐标系之间的关系可通过测量获得，因此相机坐标系与机械手坐标系之间的关系也可通过计算获得。

图6 摄像机位置Fig.6 Schematic diagram of camera position

实际工作过程中，通过摄像机观察钻机上钻杆的运行情况，选取固定在钻机上的合作目标为标志物，判断摄像机距离标志物之间的距离以及标志物的空间姿态，并将此位姿信息传输给机械臂控制器，经固定坐标变换后，控制机械手运动到指定位置，进行钻杆装卸。

3.1 单目测距模型建立

为了节省资源和使用方便，使用棋盘格标定板作为钻机上的合作目标，自定义合作目标上特征点进行距离计算。待测物为空间任意平面，参考张正友平面标定方法，根据小孔成像模型和空间成像关系，建立空间任意平面的测距模型，如图7 所示。

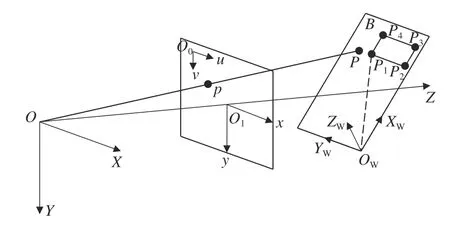
图7 空间任意平面测距模型Fig.7 Spatial arbitrary plane ranging model

其中世界坐标系建立在标定板平面B上，满足右手定则，标定板平面B为空间中任意平面，已知平面B上任意点的Zw=0，结合摄像机成像数学表达式和图7 可知：

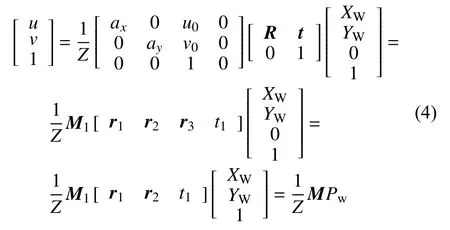
由式(4)可知，若已知平面B中4 个空间点的坐标值，代入上式建立方程组联合求解，即可得到投影矩阵M。反之，若已知投影矩阵M，即可根据空间平面B上任意点P的图像像素坐标值，求得该点的世界坐标值。针对这个模型，单目测距算法的关键是求解线性方程式(4)，步骤如下：

(1)首先，选取标定板的左上角为世界坐标系的原点，平面上的点Zw=0，标定板平面任意放置，已知标定板上各个黑白相间矩形的边长为30 mm，可计算得到标定板上角点的世界坐标。

(2)取标定板平面上距离原点坐标最近的4 个角点(P1，P2，P3，P4)，根据标定板尺寸可求得4 个点的世界坐标值。

(3)在图像中获得这4 个点相应的图像像素坐标值，根据式(4)，求解矩阵M。

(4)选取由4 个点所构成的矩形中心点为目标点，计算出目标点的像素坐标值，结合上一步已求解的矩阵M，计算该点的平移向量t。

(5)相机距离目标点的距离可转化为相机光心距目标点P的距离L：

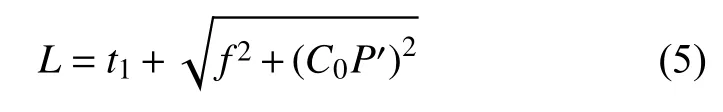
式中：C0P′为目标点在像素坐标系中的投影点P′到摄像机光心的距离。

3.2 姿态评估

通常以世界坐标系为基准，描述空间中一个物体的姿态，合作目标在空间中的姿态也是通过世界坐标系来表述，求解合作目标成像在世界坐标系中的相对关系，即为姿态的估计。设定世界坐标系固定不动，根据旋转矩阵可求出相机坐标系的旋转角，即为待测物体的旋转角。设坐标系旋转角度θ，等同于目标点绕坐标原点反方向旋转同样的角度θ。

计算时，设定物体进行定点旋转，即先围绕X轴旋转φ，然后围绕Y轴旋转θ，最后围绕Z轴旋转φ，注意逆时针为正方向。则旋转矩阵为：

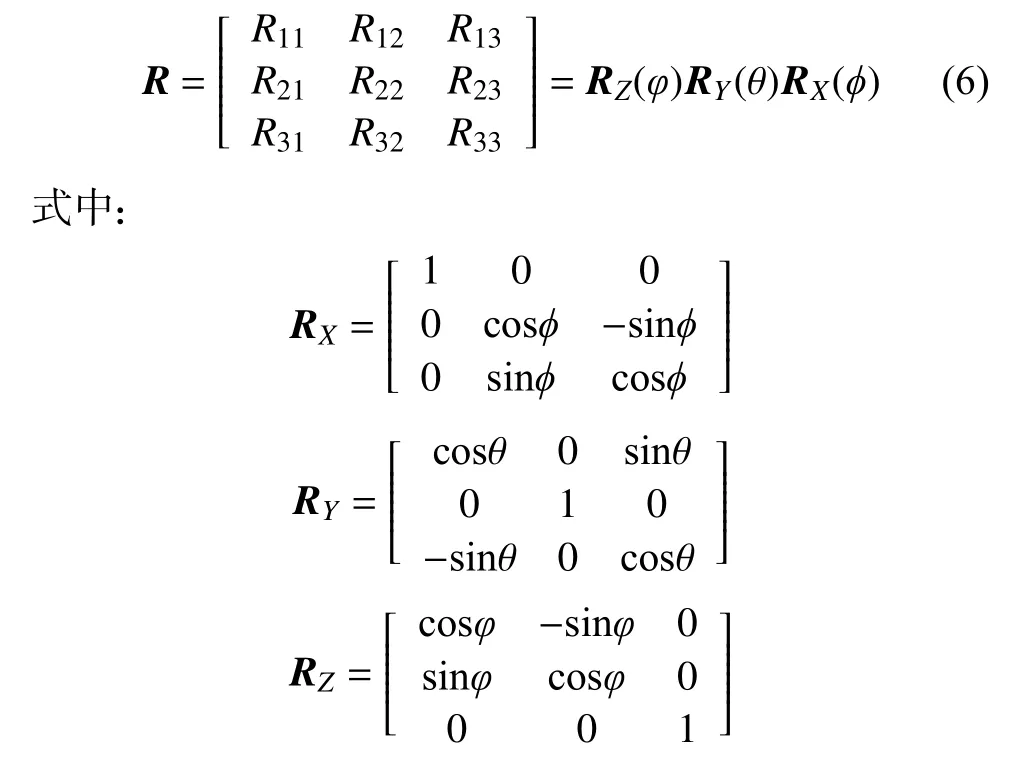
本系统中旋转角主要来自钻机自身的振动和微小移动，X轴的旋转角度范围为-90°＜φ＜90°，且φ≠±90°，合作目标姿态可由以下公式获得：

3.3 试验结果与分析

3.3.1 试验结果

2021 年11 月进行了试验。采用基于OpenCV 的VC++进行程序的编写，测距过程中，选取固定不变的棋盘格为合作目标，合作目标特征清晰，且不会因为外界环境的影响而难以识别。为了减少运算量，测距时直接选取棋盘格作为特征区域，首先存一张标定的棋盘格原始图像，特征区域选取时，采用匹配的方法，在测距图像中选定棋盘格区域定位，与标定棋盘格在世界坐标系中的选择一样，以棋盘格的左上角为世界坐标系的原点坐标，进行特征点的提取。

钻机在工作过程中，钻杆平行钻进，钻机的位置和姿态不会有太大的改变，噪声主要来源于钻机的振动和微小移动，因此引入的噪声主要为无规律的椒盐噪声，预处理后图像如图8 所示。

图8 预处理后的图像Fig.8 Pre-processed images

根据实际测试钻杆自动装卸所积累的经验数据，当识别的距离偏差大于0.2%，任意姿态角偏差大于1.2%时，钻杆装卸机械手与钻机夹持器在交换钻杆的瞬间会产生相互冲击，影响机械手抓杆精度和钻杆自动装卸系统的使用寿命。因此，钻杆装卸距离偏差不大于0.2%，任意姿态角偏差不大于1.2%，才能满足使用要求。

试验选取了6 张现场图片进行钻杆的距离测量和姿态的估计，对同一张图片进行4 次重复测距，求得其距离见表2。由于实际中准确距离不易测量，在试验时以多次测量的平均值为基准，计算单次测量值相对于平均测量值的偏差来分析视觉测量精度。从表2 中不难看出，测距的标准偏差均不大于0.12%，精度满足要求。随后对姿态角度进行3 次测量，结果见表3，绕X轴的最大标准偏差为0.12%，绕Y轴的最大标准偏差1.08%，绕Z轴的最大标准偏差为0.14%，均满足钻杆装卸的精度要求。

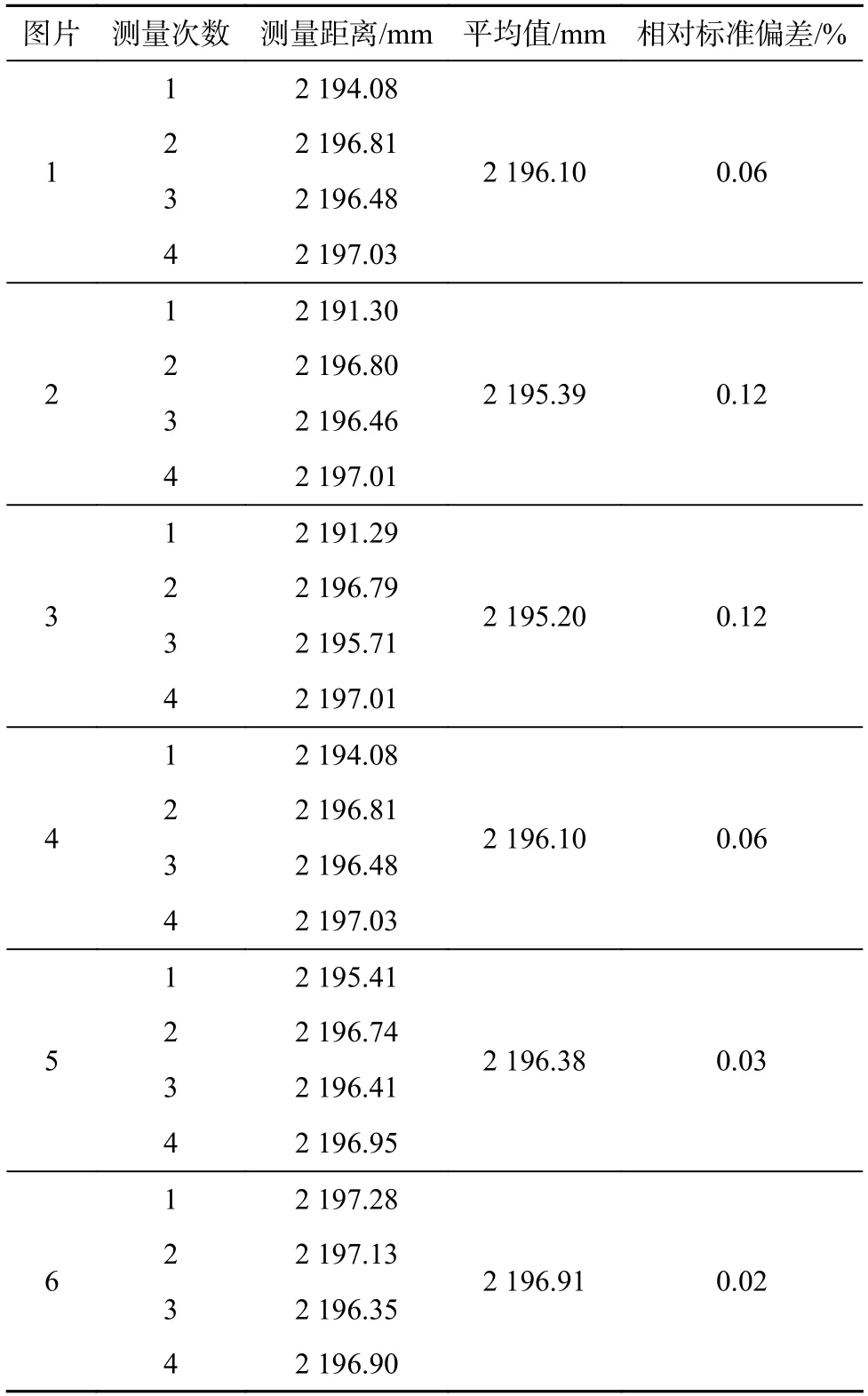
表2 距离测量结果Table 2 Distance measuring results

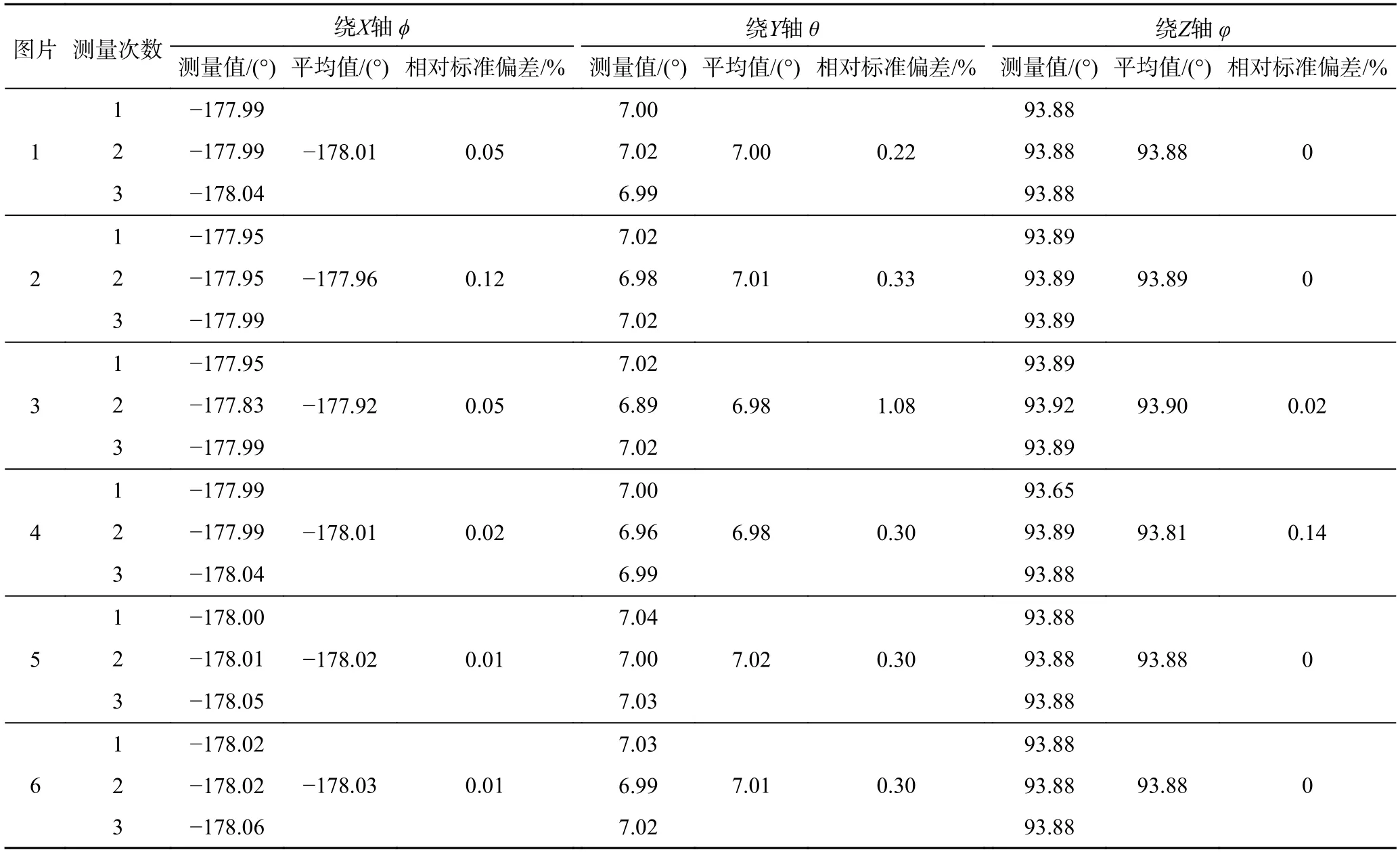
表3 姿态角度测量结果Table 3 Attitude angle measurement results

实际钻孔时，根据钻孔倾角不同，会适当调节钻机主机相对履带车体平台的倾角和高度。由于钻机主机可调范围有限，无论如何调节，最终合作目标都在摄像机的视野中心范围内。

试验中对每张照片测量的结果求平均值，引导机械手自动装卸钻杆，机械手每次都能准确地抓取到钻杆。

3.3.2 偏差分析

由于摄像机的位置是固定的，而钻机的移动仅仅由钻机工作过程中的振动和微小移动造成，所以在进行钻机的距离估计时其变化量微小。距离的测量计算在钻机工作时同步实时进行，实际距离不好测量，采用多次测量同一姿态下的相对标准偏差来验证测距的准确性。由表2 可知，经过4 次的距离测算，测距的标准偏差均不大于于0.12%，精度满足要求。

在室内进行姿态评估试验，试验过程中钻机与合作目标的姿态变化较小。轻微的振动导致的姿态变化可从表3 中看出，绕X轴的最大标准偏差为0.12%，绕Y轴的最大标准偏差为1.08%，绕Z轴的最大标准偏差为0.14%，满足钻杆装卸的精度要求。

在同一图片中进行多次测量仍会出现偏差，一是因为在标定过程中直接采用了OpenCV 库中自带的标定函数，虽然对于亚像素点的提取和畸变参数进行了修正，但还不能完全消除，导致对角点的提取有一定的偏差，且越靠近摄像机中心的偏差越小，反之，距离越远，偏差就会渐渐增大。二是因为在测距方法中，假定了棋盘格的世界坐标系是已知的，但是由于拍摄角度不同，棋盘格在摄像机上的成像会有一定的畸变，畸变后的成像点投影到世界坐标系中与原来的测量点无法完全重合，导致设定的世界坐标系存在偏差，最终导致了距离偏差。

4 结论

a.通过对国内坑道钻机钻杆自动装卸系统的分析，发现现有钻杆自动装卸系统主要依靠机械结构和接近开关进行定位，存在定位精度差和自动化程度低的问题。利用基于合作目标的单目视觉技术，建立了摄像机成像数学模型，构建了空间任意平面的单目测距模型与合作目标姿态矩阵，实现了钻杆的位姿识别。

b.试验结果表明，基于单目视觉技术的钻杆位姿识别算法真实有效，利用该方法推导的摄像机数学模型和钻杆姿态估计矩阵准确，为单目视觉技术在钻杆自动装卸领域的应用提供了参考依据，提高了钻杆自动装卸精度。

c.在后续的研究工作中，可将单目视觉技术应用于钻杆安装与拆卸的中间过程，进一步提高钻杆自动装卸系统的智能化程度。