矩形涡流发生器结构参数对圆形换热管传热特性的影响

朱世权， 胡宗要， 程传晓， 李龙江， 彭义森， 陈志华， 郑纯， 金听祥*

(1.郑州轻工业大学能源与动力工程学院， 郑州 450002； 2.南京理工大学瞬态物理国家重点实验室， 南京 210094)

在节能减排的背景下，提高能源利用效率无疑是实现绿色可持续发展的重要措施，而强化传热技术是提高换热器效率，提高能源利用效率的有效途径之一[1-2]。强化传热技术可分为：主动式、被动式和复合式[3]，主动强化传热技术需要外部能量输入，包括表面振动、脉动流和施加电磁场等[4]。被动强化传热技术不需要外部能量输入，通常包括异型管、粗糙表面和插入物等[5]。被动强化传热技术具有成本低、制造简单等特点，在工业中的应用广泛[6]。

涡流发生器是换热器最常用的被动强化传热技术之一，纵向涡强化传热技术一直是强化换热研究的重点[7]。纵向涡流发生器是涡旋平行于主流方向的涡流发生器。研究表明，纵向涡流发生器在增强传热性能方面具有显著优势，因为纵向涡流发生器诱导流体扰动产生纵向涡，干扰管芯和壁面流体的流动，并继续向下游延伸[8]。近年来，在换热通道内布置不同形状的涡流发生器得到了广泛关注。Samadifar等[9]在三角形换热通道内比较了矩形涡流发生器、斜切矩形涡流发生器、角矩形涡流发生器、Y形涡发生器和波状涡流发生器的传热性能，结果表明简单矩形涡发生器比其他形状的涡流发生器更能提高翅片换热器的换热性能。Uddip等[10]在矩形换热通道内研究了矩形涡流发生器表面纹理对传热和流动的影响，结果显示，在涡流发生器的前导面上设置多个凹型廓线有利于强化传热。Naik等[11]在矩形换热通道内研究了弯曲矩形涡发生器的流动和传热特性，发现涡流发生器前缘上部、尾缘上部和顶缘产生的纵向涡对边界层的扰动和尾迹区流体混合的改善起着重要作用。Song等[12]研究了在层流条件下平板换热器通道内布置凹、凸曲面三角形涡流发生器的换热性能，结果表明，凹型弯曲三角形涡流发生器更有利于强化传热。Sun等[13]和Zhang等[14]对圆形换热管内空气的强化传热问题进行了研究，矩形涡流发生器在管道内产生了纵向涡，增强了管内空气的混合，起到了强化传热的作用。Promvonge等[15]研究了在圆形换热管中心插入V型排布的矩形和三角形涡流发生器的传热性能，结果表明两种涡流发生器的强化传热效果均优于光滑管道，V型排布的矩形涡流发生器整体强化传热效果略优于三角形。

综上所述，使用涡流发生器强化传热的研究有很多，大多数研究是在管道壁面上安装不同形状的涡流发生器，或是在管道中心插入涡流发生器，而圆形换热管内矩形涡流发生器长高比和安装角对传热性能的影响还有待进一步研究。为此，选择在圆形换热管壁面安装矩形涡流发生器的方式，对换热管内水的加热过程进行强化，分析换热管内的传热和流动特性，研究矩形涡流发生器长高比L/H和攻角β对传热和流动特性的影响。

1 数值模拟

1.1 物理模型

内置矩形涡流发生器的圆形换热管几何模型如图1所示，圆形换热管内径D= 0.047 m，测试段长度为1 m。换热管周向布置4个倾斜的矩形涡流发生器，相邻两个涡流发生器呈V型排布，涡流发生器前缘距离测试段入口0.2 m。涡流发生器高度H和宽度分别为0.0 047 m和0.001 m，涡流发生器长高比L/H= 0.5～3，攻角β为10°～ 50°。为了保证数值计算时测试段处于充分发展段，出口不出现回流现象，将计算域向上游和下游分别延长0.5 m和0.3 m。

图1 几何模型Fig.1 Geometric model

1.2 数学模型

假设流动为稳定的、三维的和不可压缩的。利用FLUENT软件对其控制方程进行求解，采用SST(shear-stress transport)k-ω湍流模型(k为湍动能，ω为耗散率)。计算区域满足连续性方程、动量方程、能量方程以及k和ω方程，具体表达式如下。

连续性方程为

(1)

动量方程为

(2)

能量方程为

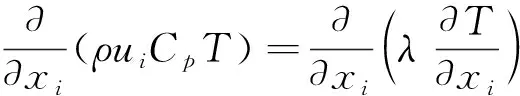
(3)

k和ω方程分别为

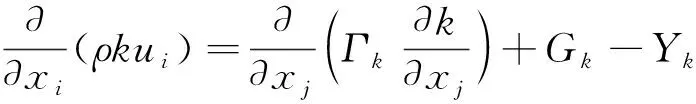
(4)

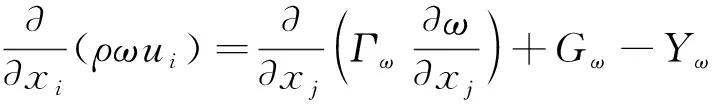
(5)

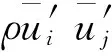
1.3 边界条件

计算域采用速度入口和压力出口，入口速度为0.2～0.6 m/s，速度方向垂直入口面，入口温度恒为293 K，所有固体壁面均定义为无滑移边界条件，延长段壁面为绝热边界条件。本研究为加热管内流体，测试段壁面为等热流边界条件，热流恒为30 kW/m2，假设涡流发生器表面的热流密度为0。工作介质水的物理性质：普朗特数Pr=7.02,ρ=998.2 kg/m3,Cp=4 183 J/(kg·K)热导率k=0.6 W/(m·K)，动力黏度η=0.001 003 Pa·s。

1.4 模型验证

为了验证数值计算方法的正确性，首先对光滑管道内的流动和传热过程进行数值模拟，并将计算结果和经验关联式进行比较，结果如图2所示。可以看出，与Gnielinski关联式[式(6)]和Dittus-Boelter关联式[式(7)]相比，努塞尔数Nu最大误差分别为7.04%和7.67%；与Filonenko关联式[式(8)]和Blasius关联式[式(9)]相比摩擦因子f最大误差分别为6.93% 和6.47%。说明所使用的数值模拟方法是可行的。

(1)Gnielinski公式为

图2 Nu和f 与关联式的对比Fig.2 Comparison of Nu and f with correlation

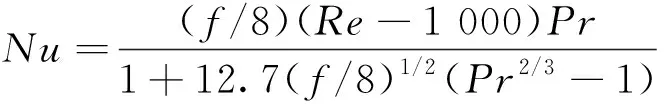
(6)

式(6)中：Re为雷诺数。

(2)Dittus-Boelter公式为

Nu=0.023Re0.8Pr0.4

(7)

(3)Filonenko公式为

f=(1.82lgRe-1.64)-2

(8)

(4)Blasius公式为

f=0.316Re-0.25

(9)

2 结果与分析

2.1 传热和流动特性分析

图3对比了涡流发生器攻角β为10°和30°两种工况下，介质流过涡流发生器的迹线。随着攻角增大，涡流发生器下游产生较大的紊乱尾迹，尾迹线呈螺旋状发展，与管道轴线相比略有偏移。攻角β为10°时，尾迹线发生少量偏移，出现了不太明显的螺旋形流迹；攻角β为30°时，涡流发生器下游的尾迹线偏移了很多，形成了非常明显的螺旋形流迹。

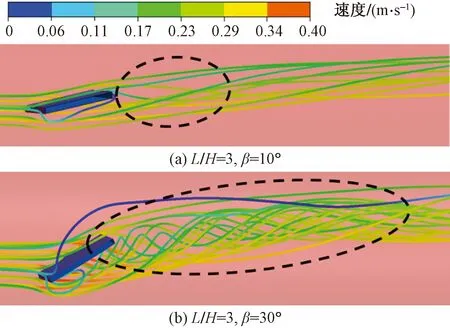
图3 涡流发生器附近流体迹线(L/H=3, Re=14 000)Fig.3 Pathlines released from near the vortex generator(L/H=3, Re=14 000)

图4为不同工况下换热管壁面Nu分布云图。由图中可知，在换热管内安装矩形涡流发生器改变了换热管壁面的Nu分布，在涡流发生器后方形成了一个具有较高Nu的带状区域，这是因为流体流过涡流发生器后，流体迹线发生了偏移和旋转(图3)，加速了冷热流体的汇合，因此换热效率也得到了提高。由图4(a)可知，随着涡流发生器长高比L/H的增大，涡流发生器后高Nu带变宽、变长，涡流发生器的强化传热效果增强。由图4(b)可知，当涡流发生器攻角β≤ 30°时，随着攻角β的增加，涡流发生器后高Nu带变宽、变长，但是β= 30°和β=50°的高Nu带形状相似，即当攻角β> 30°时，涡流发生器攻角β的增加带来的强化传热效果增加不明显。

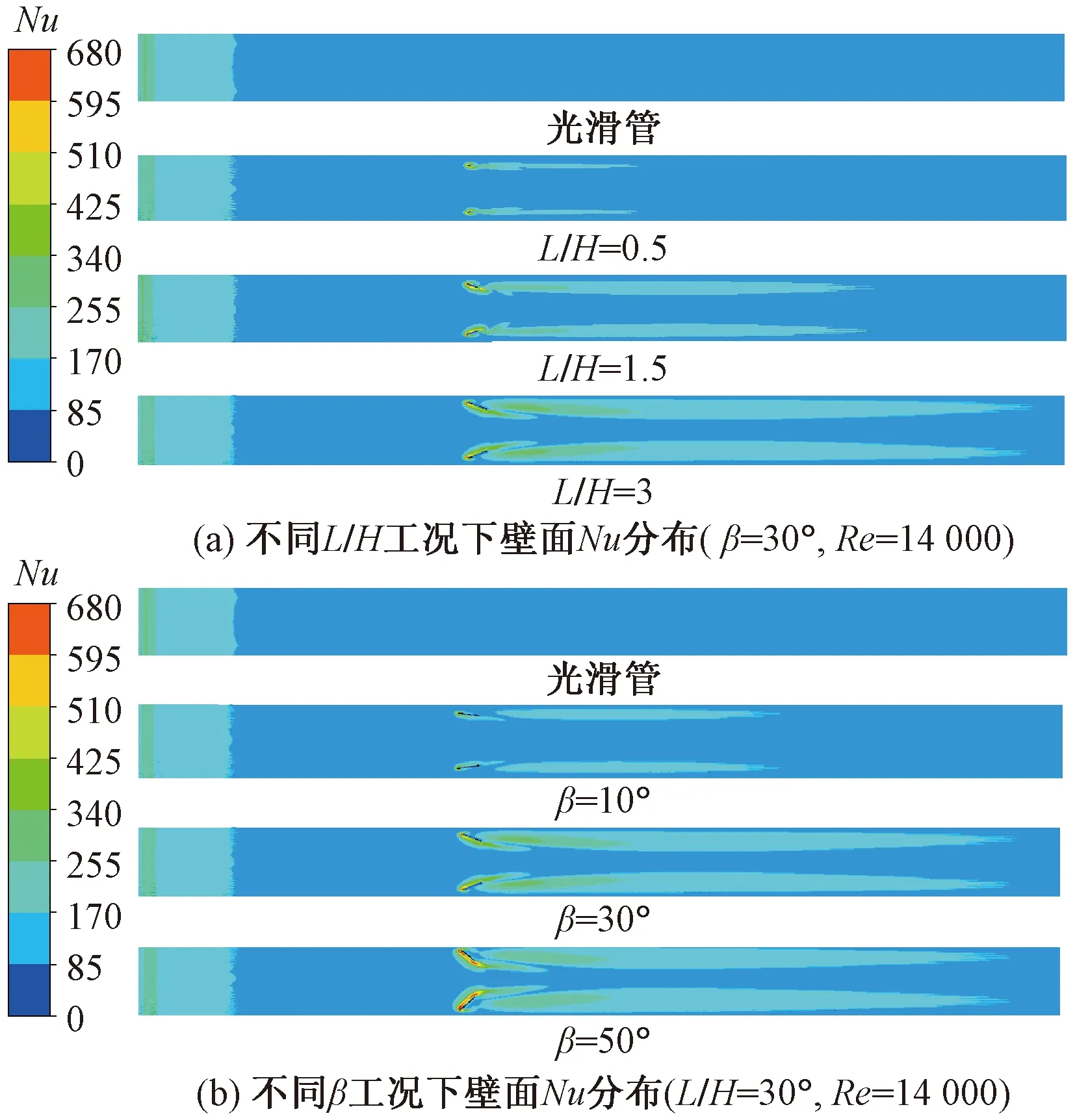
图4 不同工况下壁面Nu分布云图Fig.4 Nu distribution on the wall of different cases

图5 涡流发生器周围壁面Nu及温度分布 (L/H=3, β=50°, Re=14 000)Fig.5 Nu and temperature distribution on the wall around the vortex generator(L/H=3, β=50°, Re=14 000)

图5为长高比L/H= 3，攻角β= 50°，雷诺数Re= 14 000工况下涡流发生器周围壁面Nu和温度分布云图。可以看出，涡流发生器前侧的Nu比较高，相应的此处温度也比较低，这是因为当流体流向矩形涡流发生器时，流体对涡流发生器前部的冲刷作用，有效地破坏了边界层的形成，因而涡流发生器前部Nu较高，具有较好的换热性能。在涡流发生器的下游，存在高Nu带状区域，此处温度相对较低，说明涡流发生器诱导形成的涡流改善了此处的换热性能。

x、y、z为坐标轴的方向，在规定了坐标原点的情况下， x、y、z表示距离原点的距离图6 换热管上6个横截面处的流线 (L/H=3, β=30°,Re=14 000)Fig.6 The streamlines at 6 cross-sections of the heat exchange tube(L/H=3, β=30°, Re=14 000)

为了更清楚地了解涡流发生器产生的涡流结构及其与换热管之间的相互作用，图6展示了不同轴向位置横截面上的流线。可以看出，在z= 0.2处(涡流发生器前端)，没有清晰的湍流结构，在涡流发生器下游，即从z= 0.22处开始，管内产生了4个纵向漩涡，流体存在径向速度，破坏了近壁面区域的边界层，使得流动边界层变薄，4个纵向涡将会把壁面的热流体卷入中心流域，并把中心流域的冷流体带到温度较高的壁面，增强冷热流体的混合，加速管内换热，并且，旋流结构的产生，改善了换热管内的场协同性，从而提高了换热管的换热效率。

2.2 涡流发生器长高比L/H对传热和流动特性的影响

图7为涡流发生器攻角β= 30°时不同Re下涡流发生器L/H对Nu数的影响，与光滑管道相比，涡流发生器的使用增大了换热管的Nu，这是因为涡流发生器的使用增加了冷热流体的相互混合(图3)，增强了换热管内的场协同性(图6)。随着Re的增加，换热管的Nu增大，在相同Re工况下，涡流发生器长高比L/H越大，Nu越大。随着L/H的增大，Nu增幅越来越小，当L/H> 2后，Nu的增加不明显。

图8为涡流发生器攻角β=30°时，不同Re下涡流发生器L/H对摩擦因子f的影响，在管内壁面安置涡流发生器可以提高管内的换热速率，同样涡流的产生也会造成压力损失，使得f增大，与光滑管道相比，涡流发生器的使用增大了换热管摩擦因子f。换热管摩擦因子f随着Re的增加而减小；在相同Re工况下，涡流发生器L/H越大，f越大。

为了在等泵功基础上评价换热管的传热流动综合性能，采用性能比较指标(performance evaluation criterion，PEC)对传热管的综合性能进行分析。PEC定义为[16]

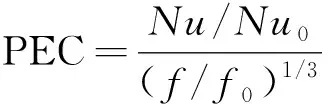
(10)

式(10)中：Nu0和f0分别为光滑圆管内平均努塞尔数和摩擦因子。

图9为涡流发生器攻角β= 30°时，不同Re下涡流发生器L/H对PEC的影响，随着Re的增大，PEC呈下降趋势，说明增加流量会降低换热管的综合性能。但在所有使用涡流发生器的工况下，PEC都大于1，这反映了安装在圆形管道中的涡流发生器在提高换热效率方面的积极作用，使用涡流发生器

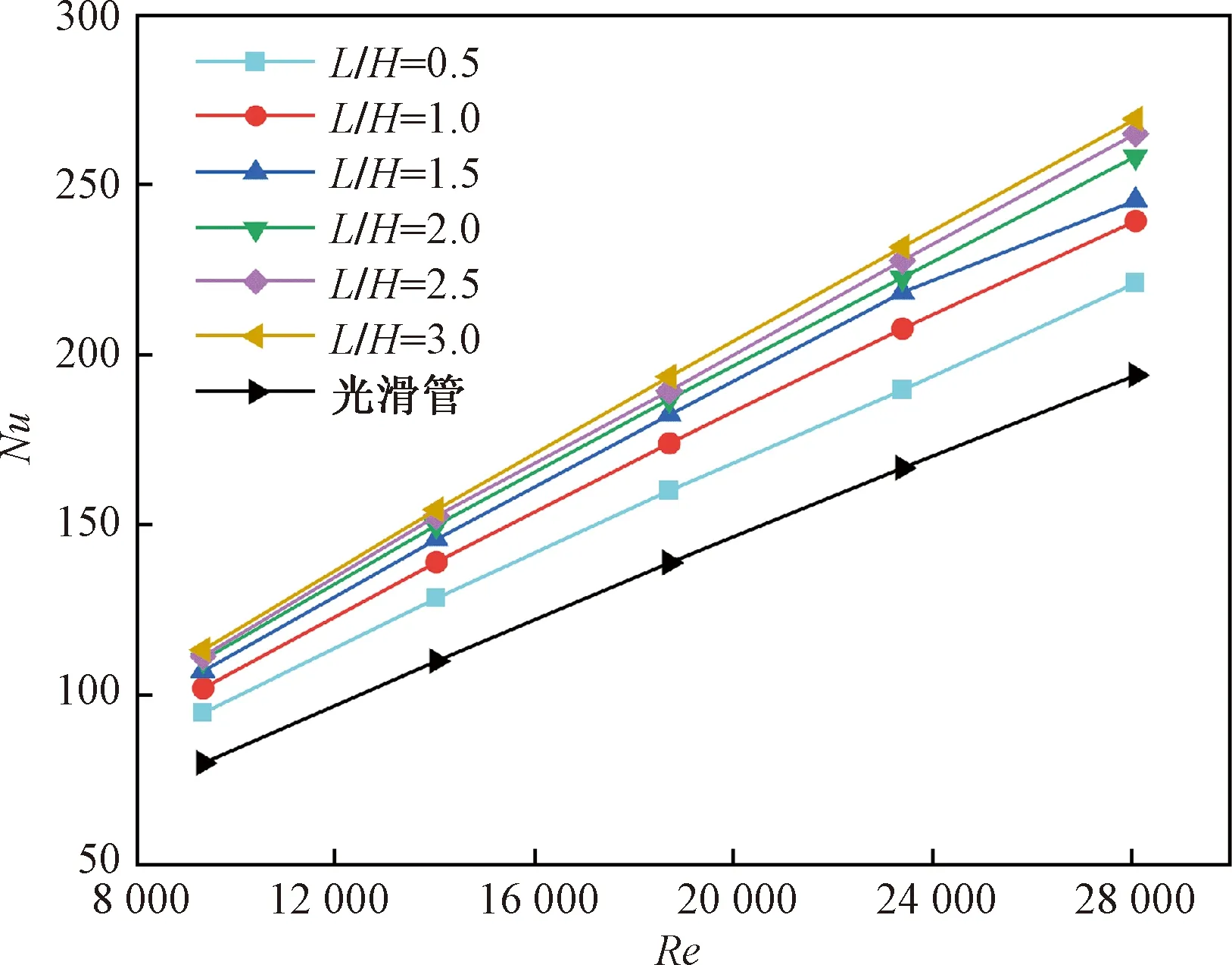
图7 涡流发生器L/H对Nu数的影响Fig.7 Effect of vortex generator L/H on Nu

图8 涡流发生器L/H对f的影响Fig.8 Effect of vortex generator L/H on f

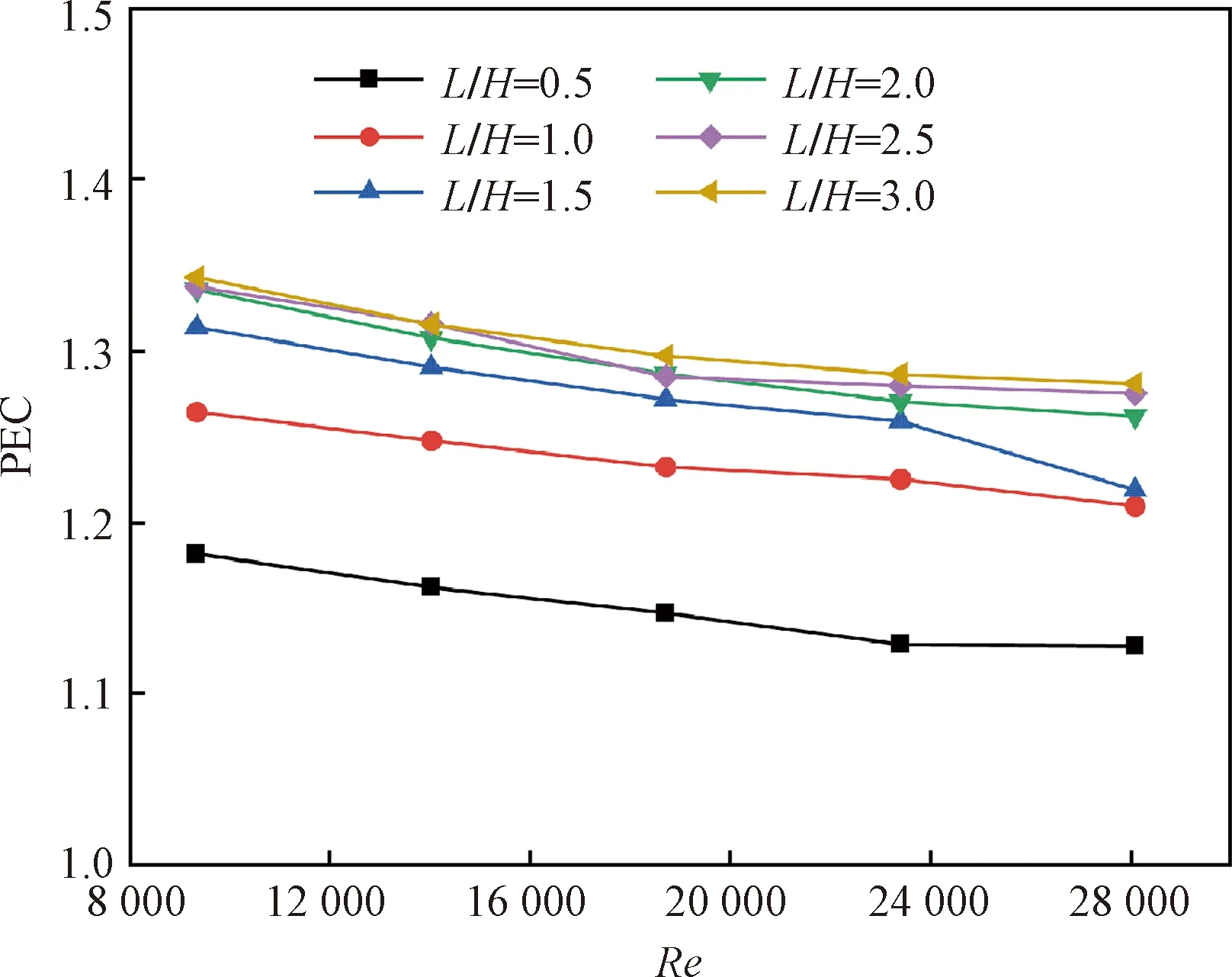
图9 涡流发生器L/H对PEC的影响Fig.9 Effect of vortex generator L/H on PEC

的管道PEC达到1.128～1.343。在相同Re下，随着L/H的增大，PEC的增加幅度逐渐减小，在L/H大于2之后，PEC的增加不明显，即当L/H=2时，换热管具有较好的综合性能。因此涡流发生器在实际应用中，为获得较高的换热效率，同时避免出现较大的压降，应采用合适的长高比。

2.3 涡流发生器攻角β对传热和流动特性的影响

图10为涡流发生器L/H=3时，不同Re下涡流发生器攻角β对Nu的影响，与光滑管道相比，涡流发生器的使用增大了换热管的Nu。随着Re数的增加，换热管的Nu增大。在相同Re工况下，当攻角β≤30°时，Nu随攻角的增加而增大，这是因为随着攻角的增加，涡流发生器后产生的螺旋状尾迹区域增大所致(图3)。当攻角β>30°时，随着攻角的增大，Nu几乎没有变化甚至略降低，虽然更大的攻角会导致更强烈的旋流，但过大的攻角会使得涡流发生器所诱导产生纵向涡旋的涡度矢量的切向分量过小，相比较攻角β=30°而言，纵向涡旋的强度并没有得到增强，因此，Nu的变化很小，图4(b)也印证了这一点。

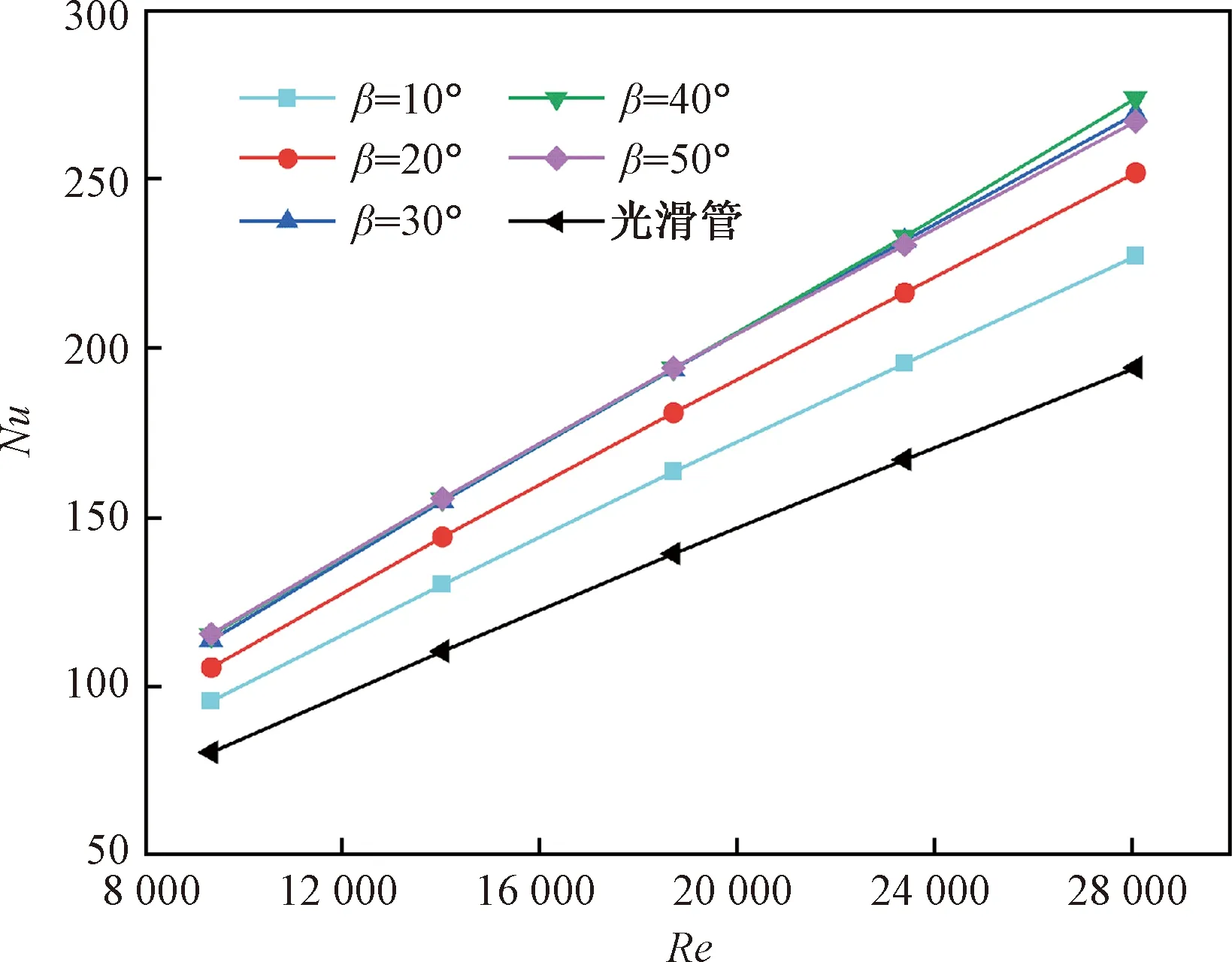
图10 涡流发生器攻角β对Nu的影响Fig.10 Effect of attack angle β of vortex generator on Nu

图11为涡流发生器L/H=3时，不同Re下涡流发生器攻角β对f的影响，与光滑管道相变，涡流发生器的使用增大了换热管的f。换热管的f随着Re的增加而减小，在相同Re工况下，涡流发生器攻角β越大，f越大，随着攻角β的增加，f的增幅越来越小，说明大攻角情况下，攻角的增加带来的阻力增加不明显。

图12为涡流发生器L/H=3时，不同Re下涡流发生器攻角β对PEC的影响，PEC变化范围为1.149～1.351，均大于1，这反映了安装在圆形管道中的涡流发生器在提高换热效率方面的积极作用。随着Re数的增大，PEC呈下降趋势，在相同Re数下，随着攻角β的增大，PEC先增大后减小，当攻角β=30°时，多数工况下PEC具有最大值，换热管具有最佳综合性能。

图11 涡流发生器攻角β对f的影响Fig.11 Effect of attack angle β of vortex generator on f

图12 涡流发生器攻角β对PEC的影响Fig.12 Effect of attack angle β of vortex generator on PEC

3 结论

对内置矩形涡流发生器的圆形换热管进行了数值模拟研究，得到了涡流发生器长高比L/H和攻角β对Nu、f和PEC的影响规律，通过对换热管内的流动和传热性能进行分析，得出如下结论。

(1)流体介质在涡流发生器下游产生了螺旋形流迹，换热管内产生了4个纵向漩涡，加速了冷热流体的汇合，改善了换热管内的场协同性，提高了换热管的换热效率。

(2)在涡流发生器攻角β=30°，相同Re工况下，随涡流发生器L/H的增大，Nu增幅越来越小；涡流发生器L/H越大，f越大；随着L/H的增大，PEC的增加幅度逐渐减小，当L/H=2时，换热管具有较好的综合性能。

(3)在涡流发生器长高比L/H= 3，相同Re数工况下，攻角β对Nu和f均有较大的影响，随着攻角β的增大，PEC先增大后减小，当攻角β=30°时，多数工况下PEC具有最大值，换热管具有最佳综合性能。