基于ISRSAC 的两类代理多重数字签名方案*

刘天宁 张艳硕 刘 宁

北京电子科技学院，北京市100070

1 引言

在1977 年，三位美国的数学家Rivest、Shamir 和Adleman［1］联合提出了RSA 公钥加密体制。 RSA 算法是世界上第一个实用的公开密钥的算法。 它的安全性依赖于大整数因子分解的困难性。 2018 年 3 月， Tangavel 和Varalakshmi pro［2］提出了“用于云数据机密性的改进RSA 安全密码系统（ISRSAC）”，并且在他们的论证下，ISRSAC 被证明比RSA 更安全。

文献［3］表明，在现实世界里，人们常需要将自己的某些权力委托给可靠的代理人，让代理人代表本人去行使这些权力。 在这些可以委托的权力中包括人们的签名权。 1996 年，Mambo、Usuda 和Okamoto［4］提出了代理签名的概念，给出了解决这个问题的一种方法。 由于代理签名在实际应用中起着重要作用，所以代理签名一提出便受到广泛关注，国内外学者对其进行了深入的探讨与研究。 有时候，我们会遇见多个人委托同一个人的情形，这种情况下的签名我们称为代理多重签名。

ISRSAC 算法是一种安全性高于传统RSA算法的新型算法，因此借其设计的签名算法会具有更高的安全性。 目前对ISRSAC 算法的性能分析表示其安全性要高于传统RSA 密码体制，同时有关于它的密码体制研究、数字签名设计在理论上也可以应用于云数据存储、传输等方面。2015 年，Thangavel 和Varalakshmi［2］提出了增强RSA 安全密钥生成方案，其中使用四个素数来提高安全性即ESRKGS 算法。 2018 年3 月，Thangavel 和Varalakshmi［2］将ESRKGS 算法修改为ISRSAC 方案。 2021 年，Teng Yang［5］等人以ISRSAC 算法为基础给出了一种基于ISRSAC公钥密码算法的数字签名方案然后构造了一个代理数字签名方案、一个有序多重数字签名方案和一个广播多重数字签名方案。

在本文中，首先介绍了ISRSAC 算法，然后在Teng［5］等人签名方案的基础上将其扩展到代理多重签名，并且设计了按序代理多重签名以及广播代理多重签名，最后针对其安全性进行分析。 结果表明其在安全性上等同于Teng Yang［5］等人签名方案，同时增加了代理多重签名的性质。 在两类代理多重签名方案中，一个代理签名人可以同时代表多个原始签名人的利益在一个文件上签名，签名的方式也可以按照一定顺序或者不分前后顺序来选择，这使得方案在电子商务、网络安全通信、多方公平交换协议、电子选举协议以及移动代理环境方面有较为广泛的应用前景。

2 ISRSAC 算法

2.1 RSA 算法

公钥密码学［6］由于它在数字签名、认证和密钥管理上的优越性，在现代保密体系中占据十分重要的地位，应用十分广泛，其中RSA 是目前公认的在理论和实际应用中最为成熟和完善的一种公钥密码体制。 它不仅可以进行加密，还可以用来进行数字签名和身份验证，是公钥密码体制的代表。 它是由Rivest、Shamir 和Adleman［7］于1977 年在剑桥麻省理工学院开发设计的。RSA 密码系统描述如下：

具体算法流程如下：

（1）随机选取两个大素数p 和q，其中p≠q，p ＞3，q ＞3 然后计算n ＝p·q；

（2）计算n 的欧拉函数值：

φ（n）＝（p－1）（q－1）

（3） 选择数字e 作为公钥，同时gcd（e，φ（n））＝1，计算私钥d，满足e·d≡1modφ（n）

（4）公钥为（e，n），私钥为d。

加密过程：假设M 是明文信息，则可以得到密文C≡Memodn。

解密过程：如获取密文信息C，明文信息获取如M≡Cdmodn。

RSA 的安全性［8］基于大整数N 因子分解的难度。 一旦N 分解为两个素数因子，RSA 就被破解。 但数学上至今还未找到分解一个具有大素数因子的大数的有效办法，也不能证明这种分解就是NP 问题。 从长远来看，对于RSA 长密钥攻击力强度会越来越强，量子计算机的出现和因子分解算法的不断改进会给RSA 安全带来更大的威胁，所以取一个1024 或2048bits 的密钥才能保证RSA 更好的安全性。

2.2 ISRSAC 公钥算法

RSA 密码体制的安全性基于大整数因式分解问题。 随着各项技术的不断发展，传统RSA算法的安全性正遭受威胁。 为了提高RSA 系统的安全性，大部分研究人员基本从增加额外的素数、添加随机数和隐藏公钥等方面对系统进行修改。 而ISRSAC 算法在RSA 的基础上对加强了大整n 的分解难度并增加了随机性从而加大了算法计算上的破解难度。 ISRSAC 密码系统由以下三个阶段组成：主密钥生成、加密和解密［5］。

具体算法流程如下：

（1）随机选取两个大素数p 和q，其中p≠q，p ＞3，q ＞3 然后计算

n ＝p·q·（p－1）·（q－1），m ＝p·q。

（2）随机选取一个整数r，其中p ＞2r ＜q，生成

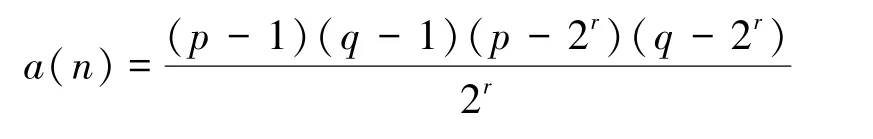
（3）选择数字e，满足1＜e ＜a（n） 同时gcd（e，a（n））＝1，计算私钥d，满足

e·d≡1moda（n）

（4）公钥为（e，n），私钥为（d，m）。

加密过程：假设M 是明文信息，则可以得到密文C≡Memodn。

解密过程：如获取密文信息C，明文信息获取如M≡Cdmodm。

签名方案的安全性很大一部分是取决于核心算法的安全性，相较于基础传统的RSA 密码体制，ISRSAC 有着较高的安全性，主要体现在以下两个方面：

（1） 此方案强化了大整数的分解问题，即在n 的取值上将原本依赖于两个素数的生成方式，拓展到两个素数加两个自然数，这样就很难用现有的方法进行因式分解进而破解获取私钥。 首先n 的取值包含两个素数和两个自然数，目前因式分解的方法包括the elliptic curve factorisation method（椭圆曲线因式分解）、General Number Field Sieve method（一般数域筛法），但都很难用于对同时包含两个素数和两个自然数的n 进行分解，由于两个自然数因子的存在就很难找到相关的两个大素数p，q。 当然想要计算出私钥d，仅仅只靠计算n 值是不够的，还需要确定随机因子r，由于r 值的确定是充满随机性的，所以攻击者很难分解n 的同时找到随机数r 进而获取到私钥d 的具体值。

（2） 在私钥生成过程中定义了一个新的安全函数α（n），在这个函数中引入了随机值r，所以攻击者在没有获取到r 的情况下即便解决了上述的因式分解问题，在进一步的计算上也会存在一定困难。 由上述两点可以得出ISRSAC 算法相较于RSA 算法是安全的，但在密钥生成及加解密操作上需要的时间是较长的，不过以此来换取较高的安全性在实际操作上肯定是可以忽略的。

2.3 基于ISRSAC 的多重广播签名

2021 年1 月，Teng Yang［5］等人有提出一个基于ISRSAC 的广播多重数字签名方案，本文接下来即会介绍一下该方案。

2.3.1 系统建立

首先，一个权力中心需要随机选择两个大素数p 和q，其中p≠q，p ＞3，q ＞3 然后计算n ＝p·q·（p－1）·（q－1），m ＝p·q。

然后如上述流程一样，选择r 和e，找到a（n）和d，之后，权力中心集（e， n） 作为公钥，（d，m）作为私钥。 H（·）为哈希函数，Ui代表签名者，M 为明文，IDi（i ＝（1，2，…），n） 表示签名者的身份同时是公开的。

为了使签名者Ui能够正确地签名消息M，权力中心计算：

hi ＝H（IDi），

Si≡hi－dmodn，

通过一个秘密的安全通道将证书（IDI，Si）分发给每个签名者Ui， 每个签名者使用公式hiSie≡modm来验证证书（IDI，Si）。

基于上述理论，我们可以完成一个广播式多重签名，Uc 代表签名的收集方。

2.3.2 签名生成

（1）每一个签名者Ui（i ＝（1，2，…n）） 选择一个随机数r，计算

Ri≡riemodn

将Ri发送到Uc；

（2）Uc 计算

K≡R1R2…Rnmodn

然后广播发送K；

（3）每个签名者Ui计算

l ＝H（K，M），

Di≡riSlimodn

然后发送Di至Uc。

2.3.3 验证签名

接受Uc 计算D ＝D1D2…Dn， 最终的签名为（D，K，l）。

当我们想要验证这个签名时，需计算：

h1＝H（ID1），…，hn ＝H（IDn），

K′≡De（h1·h2…hn）lmodm，

l′ ＝H（M，K′）

如果l′ ＝l，则这个签名被认证成功。

以下是针对此方案的安全性分析：

（1）签名方案的安全性很大一部分是取决于核心算法的安全性，由本文2.2 节可以了解到，ISRSAC 算法由于自身因式分解的复杂度加上随机性的引入，算法本身就有很高的安全性。攻击者无论从各种方面进行入侵，都很难获取签名方所使用的私钥，这样就避免了冒充攻击的可能性。 所以在核心算法上，基于ISRSAC 算法的安全性较高，要强于基于传统RSA 算法的数字签名。

（2）本方案是基于ISRSAC 大整数因式分解难题和哈希函数求逆困难性提出来的，虽然每个签名者Ui的身份IDi是公开的，任何人都可以计算H （IDi），但是任何人却不能计算Si≡hi－dmodn，，因为两个大素数p，q，所以没有人可以通过e 来得到d 的信息，求解d 的难度等价于ISRSAC 难题。

（3）本方案引入了hash 函数，它是通过散列法将任意长度的输入信息变换成固定长度的消息摘要。 签名者对消息摘要进行签名不但可以提高签名效率，而且还可以保证信息完整性和防止隐私信息泄露。

（4）本方案可以抵抗外部攻击，任何外部成员要想伪造Ui 的签名是不可行的。

假设外部攻击者想伪装成签名者Ui来对消息M 签名，由上面的签名过程可知，他可以随机选择Ri，但是密钥中心拒绝接受他发送的Ri，因为他不能发送合法的身份证书Si。

3 代理多重签名

目前，人们已提出了若干不同类型的代理签名方案。 但是在这些方案中，一个代理签名者只能代表一个原始签名者。 有时，人们需要让一个代理签名者能够同时代表多个原始签名者。 文献［4］表明，在现实的生活中，由于某些不可抗力人们可能没法亲自来签署某些文件，而需要自己能够信任的人代理签名。 就像我把自己的公章锁了起来，将钥匙托付给了代理人，让他代替我给一些需要处理的文件盖章。 对于前一种情况，可用多重签名方案来解决，针对后一种情况，即多个部门同时委托一个代理人在一个文件上签名。 例如：如果一个公司将要发布一个涉及到财务部门、工程部门以及行政管理部门的文件，该文件必须由这些部门联合签名才有效，这些部门可以委托他们都信任的代理人代替他们在该文件上签字。 对于这种情况，可用代理多重签名方案来解决，即多个部门同时委托一个代理人在一个文件上签名。 这使得代理多重签名在电子商务和网络安全通信方面有较为广泛的应用前景。

1996 年，Mambo［9］等人提出了代理签名的概念。 代理签名是一种特殊的签名体制，它满足通信三方（原始签名者、代理签名者和接收方）之间的安全需求，并为这三方通信提供了便利，因此它的安全性得到研究者们的广泛重视。2000 年伊丽江等人［10］提出了代理多重签名概念；同年祁明等人［11］提出了基于离散对数的若干新型代理签名方案；王晓明等人［12］在祁明等人方案的基础上提出了一种代理多重数字签名方案；2015 年冯婕等人［13］提出了具有强不可伪造性的双向代理重签名方案；2017 杜成斌［14］提出了量子代理多重盲签名协议设计；同年曹阳［15］提出了基于ECC 存在特权集的（t，n）门限群代理多重签名方案；2018 年郑建国［16］等人提出了一种优化的代理多重数字签名方案，该方案可以抵抗合谋攻击和伪造攻击；2020 年李文婷［17］提出了一种基于代理重加密的区块链电子病历数据共享算法。 可以看出目前基于离散对数的代理多重签名研究占多数，而基于大整数分解的代理多重签名研究较少，本文所提出的研究正可以弥补这一领域的空白。

3.1 代理多重签名一般方案

2000 年伊丽江等人［10］提出的代理多重签名方案如下：

令A1，…An是n 个原始签名人。 他们联合请求一个代理签名人B 代替他们在一个文件m上签名。 对1 ≤∀i≤n，Ai有一个公开密钥vi和一个秘密密钥si，使得si∈RZp－1＼｛0｝，vi≡gsimodp。

3.1.1 系统参数

对1 ≤∀i≤n， Ai随机选择ki∈RZp－1＼｛0｝，计算Ki≡gkmodp和σi≡si ＋kiKimodp－1。

Ai将（σi，Ki） 作为子密钥通过安全信道交给B。 B 验证gσi≡viKkiimodp是否成立。 如果成立，他接受这个密钥，否则他拒绝接受这个密钥而请求Ai重新发送一个有效的子代理密钥，或者他终止协议。 如果B 确认所有（σi，Ki）（1≤∀i≤n）都是有效的，那么他计算出σ ＝σi。

3.1.2 代理签名生成

当Bob 代表所有原始签名人A1，…An在文件m 上签名时，他用σ 作为普通签名运算中的签名秘密密钥来执行普通的签名运算。 于是生成的代理签名是（m，Signσ（m），K1，…Kn）， 其中Signσ（m） 表示用普通签名方法在密钥σ 下生成的关于消息m 的签名。

3.1.3 代理签名验证

验证人在验证以上代理签名时首先计算v′≡v1…vnKK11…KK1nmodp， 然后用v′作为一个新的公钥对Signσ（m） 进行验证。

以上代理多重签名方案满足以下性质：

性质1 代理签名人无法计算出任何一个原始签名人的秘密密钥。

性质2 任何人可以验证代理多重签名的有效性。

性质3 通过有效的代理多重签名，验证者可以确认每个原始签名人对被签文件都是承认的，这是因为，在验证代理多重签名时，需要用到每个原始签名人的公钥。

性质4 在没有得到所有原始签名人的授权情况下， 任何人都无法生成一个有效的代理多重签名。

2000 年伊丽江等人［10］提出的代理多重签名方案原则上所有原始签名人都信任代理签名人。 代理签名人无法计算出原始签名人的秘密密钥，因而无法伪造任何一个有效的代理签名，所以任何人都不能伪造出有效的代理签名。

另外，在验证代理签名时必须使用每个原始签名人的公钥，所以从一个有效的代理签名可以确认每个原始签名人都介入了签名过程，因此实现了一个签名可以代表多个原始签名人的目的。

3.2 代理多重签名的基本性质

与基本的代理签名体制类似，代理多重签名应当满足以下基本性质［10］：

（1）基本的不可伪造性。 除了原始签名人外，任何人（包括代理签名人）都不能生成原始签名人的普通数字签名。

（2）代理多重签名的不可伪造性。 除了代理签名人外，任何人（包括原始签名人）都不能生成有效的代理多重签名。 特别是，如果原始签名人委托了多个代理签名人，那么任何代理签名人都不能伪造其它代理签名人的代理多重签名。

（3）代理签名的可区分性。 任何一个代理多重签名都与原始签名人的普通（多重）签名有明显的区别；不同的代理签名人生成的代理多重签名之间也有明显的区别。

（4）不可抵赖性。 任何签名人（不论是原始签名人还是代理签名人）在生成一个（代理）多重签名后，不能再对它加以否认。

（5）身份证实性。 每个原始签名人都可以根据一个有效的代理多重签名确定出相应的代理签名人的身份，或者多个原始签名人合作起来可以确定出代理签名人的身份。

（6）密钥依赖性。 生成代理多重签名的签名密钥依赖于每个原始签名人的秘密密钥。

（7）可注销性。 任何一个原始签名人都可以注销他委托给代理签名人的签名权力。

4 基于ISRSAC 算法的按序代理多重签名方案

按序多重签名是指按同一顺序对多个用户的签名和授权消息文件［5］。 例如，在一个公司里，有一份要求董事长、总经理和部门经理一起签署的合同才是有效的。 在看到部门经理的签字后总经理只签了合同。 董事长承认总经理和总经理部门经理的签字。 基于类似产品的需要在场景中，按序多重签名也被广泛使用。

4.1 系统参数

随机选取大素数pAi（1 ≤i≤n），pBi（1 ≤i≤n），pCA，qAi（1 ≤i≤n），qBi（1 ≤i≤n），qCA其中所有的p≠q，p ＞3，q ＞3。

令原始签名人为Ai（1 ≤i≤n），代理签名人为Bi（1 ≤i≤n），nAi、nBi、nCA、mAi、mBi、mCA分别为Ai、Bi和CA 的ISRSAC 模数，分别计算：

nAi ＝pAi·qAi·（pAi－1）·（qAi－1）

nBi ＝pBi·qBi·（pBi－1）·（qBi－1）

nCA ＝pCA·qCA·（pCA－1）·（qCA－1）

mAi ＝pAi·qAimBi ＝pBi·qBi

mBi ＝pBi·qBimCA ＝pCA·qCA

mCA ＝pCA·qCA

随机选取ri（1 ≤i≤n）pAi ＞2ri ＜qAi，其中CA 选择其中ri（1 ≤i≤n） 中任意值。

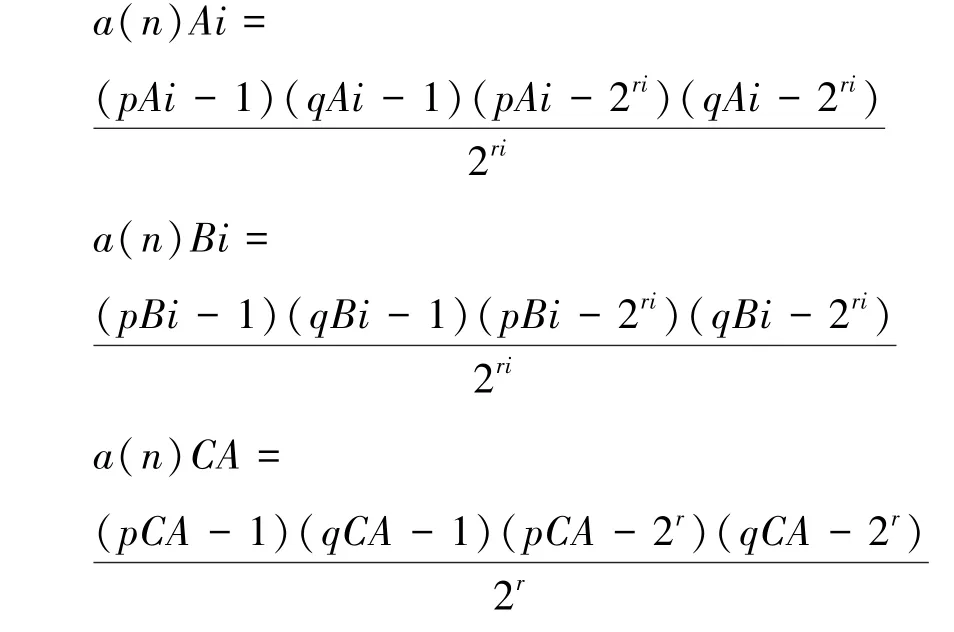
选择数字e，满足1＜e ＜a（n） 同时gcd（e，a（n））＝1， 计算私钥d，根据公式e·d≡1moda（n） 计算出公私钥。

（eAi，mAi） 为Ai公钥， （dAi，nAi） 为Ai私钥，（eBi，mBi） 为Bi公钥， （dBi，nBi） 为Bi私钥，（eCA，mCA） 为CA 公钥，（dCA，nCA） 为CA私钥。mw为授权信息，其中含有原始签名人和代理签名人的身份、代理权限、授权有效期等内容。IDAi，IDBi分别表示Ai和Bi的身份标识，且公开。 本文选取的哈希算法为SM3 算法。 SM3是中国独立开发的哈希算法，其安全性相当于sha－256。 因此，本方案选择SM3 作为签名的哈希函数。

由CA 选取小素数epA为临时公钥，发送至每个原始签名人Ai。 对于1 ≤∀i≤n，每个Ai分别计算epAdpAi≡1moda（n）Ai，

再计算：

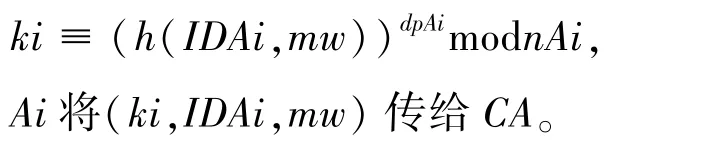
CA 逐一验证kiePAmodmAi≡h（IDAi，mw）是否成立。 如果成立，则（ki，IDAi，mw） 为一个有效的子代理密钥；如果不成立，则CA 拒绝接受该密钥，并要求Ai重发一个新的子代理密钥，或者停止协议。

CA 计算

通过安全信道将（ki，si） 发送至代理签名人Bi，ki－1 发送至Bi，ki作为Bi的部分代理公钥，并将mw、IDAi和IDBi向所有用户广播。

4.2 代理签名的生成

公布Bi签名顺序，假设为（B1，B2，…，Bn）：

（1）代理签名人B1 选择一个随机数r1（1 ≤r1 ≤n），计算：

（2）将（T1，v1，D1） 传递给B2，B2 验证签名正确性：

h1＝h（ID1，mw，k1）

T1*≡D1eCA·h1v1modmCA

v1*＝h（m，T1*）

如果v1*＝v1，则签名正确，否则签名不正确。 当验证的签名通过后，B2 随机选取一个数r2（1＜r2＜n），并计算

T2 ≡r2eCAmodnCA v2＝h（m，T2）

D2 ≡D1r2s2v2modnCA

f1 ≡h1v1modnCA

将（T2，v2，D2，f1） 传递给B3，以此类推。

（3）当签名人Bi（2＜i ＜n） 将签名（Ti，vi，Di，fi－1） 传递给Bi ＋1（fi－1 ≡fi－2hi－1vi－1modnCA），Bi ＋1 首先验证签名正确性，计算：

hi ＝h（IDi，mw，ki）

Ti*≡DieCA·fi－1hivimodmCA

vi*＝h（m，Ti*）

如果vi*＝vi， 则签名正确，否则签名不正确。 当验证的签名通过后，Bi ＋1 随机选择一个数ri ＋1（1＜ri ＋1＜n），并计算

Ti ＋1 ≡Tiri ＋1eCAmodnCA

vi ＋1＝h（m，Ti ＋1）

Di ＋1 ≡Diri ＋1si ＋1vi＋1modnCA

fi≡fi－1hivimodnCA

将（Ti ＋1，vi ＋1，Di ＋1，fi） 传递给下一个签名人，执导最后一个签名人为止。 最后得到消息m 的代理多重签名为（Tn，vn，Dn，fn－1）。

4.3 代理签名的验证

当验证者验证消息的签名（Tn，vn，Dn，fn－1） 时，计算：

hn ＝h（IDn，mn，kn）

Tn*≡DneCA·fn－1hnvnmodmCA

vn*＝h（m，Tn*）

如果vn*＝vn，则签名正确，否则签名无效。

本方案的安全性在第6 节中进行具体分析。

在实际应用中，多重签名往往是按有序进行签名的［18］，按序多重签名是指签名者将自己的签名按照一定顺序发送给签名接收者，由签名接收者整理产生对消息的签名。 代理多重签名可以应用于多个部门同时委托一个代理人在一个文件上签名［10］。 按序代理多重签名可以应用于多个部门同时委托一个代理人在一个文件上签名，而签名需要先后顺序。

按序代理多重签名可以应用于类似于以下案例的场景：

例如，公司的经理、财务和出纳集体出差或者单位各部门上下级领导集体出差，需要他们对同一文件的进行有序签名，那么可以指定一个他们都信赖的人代表他们签名。

5 基于ISRSAC 算法的广播代理多重签名方案

在许多情况下，很多人需要签署相同的文件［5］。 例如，在一个车载网络中，每个机载的通信单元需要签署相同的事件。 在电子商务方面，有一些机构需要签署同样的协议文件。 应用程序场景中需要的签名是多重签名的对象。 广播多重签名是一种表单的多重签名。 其特点是每个签名方都将其部分签名传递给信号收集器。收集器将收集部分内容签名，然后执行验证。 如果验证了所有的属性，那么可以验证多个签名合成，否则不可以使用它们。

基于同样思想，构造一个广播代理多重签名，令Br为接收者，其他参数同按序代理多重签名。

5.1 系统参数

由CA 选取小素数epA为临时公钥，发送至每个原始签名人Ai。 对于1 ≤∀i≤n每个Ai分别计算epAdpAi≡1moda（n）Ai，再计算：ki≡（h（IDAi，mw））dpAimodnAi，Ai将（ki，IDAi，mw）传给CA。

CA 逐一验证kiePAmodmAi≡h（IDAi，mw）是否成立。 如果成立，则（ki，IDAi，mw） 为一个有效的子代理密钥；如果不成立，则CA 拒绝接受该密钥，并要求Ai重发一个新的子代理密钥，或者停止协议。

CA 计算

hi ＝h（IDBi，mw，ki）

si≡hi－dCAmodnCA

通过安全信道将（ki，si） 发送至代理签名人Bi，si作为Bi的部分代理公钥，并将mw、IDAi和IDBi向所有用户广播。

5.2 代理签名的生成

（1）每个代理签名人Bi选择一个随机数ri，计算Ri≡rieCAmodnCA， 将Ri发送给接收者Br。

（2）接收者计算T≡R1R2…RnmodnCA，将T 广播出去。

（3）每个签名人Bi计算

v ＝h（m，T）

Di≡risivmodnCA

把Di传送给接收者Br。（4）接收者Br计算

D ＝D1D2…Dn，

最后签名为（D，T，v）。

5.3 代理签名的验证

验证时，验证者先计算时，计算

h1＝ h（IDB1，mw，k1），…，hn ＝ h（IDBn，mw，kn），

再计算

T*≡DeCA（h1h2…hn）vmodmCA

v*＝h（m，T*）

如果v*＝v，则签名正确，否则签名无效。

本方案的安全性在第六节中进行具体分析。

广播多重签名［19］是指签名者将自己的签名不分先后顺序发送给签名接收者，由签名接收者整理产生对消息的签名。 代理多重签名可以应用于多个部门同时委托一个代理人在一个文件上签名［10］。 广播代理多重签名可以应用于多个部门同时委托一个代理人在一个文件上签名，而签名不分先后顺序。

广播代理多重签名可以应用于以下案例的场景：

例如， 一个公司发表的声明涉及到财务部、开发部、销售部、售后服务部等部门，需要这些部门签名认可，而签名不分先后顺序，这些部门指定一个它们都信赖的人或部门代表它们签名，与这些部门共同生成多重签名相比，其效率大大提高。

在两类代理多重签名方案中，一个代理签名人可以同时代表多个原始签名人的利益在一个文件上签名，而且可以采用按序和广播的方式，这使得方案在电子商务和网络安全通信、多方公平交换协议、电子选举协议以及移动代理环境方面有较为广泛的应用前景。

6 安全性分析

（1）不可伪造性

这两种方案在代理授权阶段的方法基本类似，都是通过可信的认证中心CA 验证原始签名人的授权后，计算hi ＝h（IDBi，mw，ki）si≡hi－dCAmodnCA来生成代理密钥；在生成与验证代理多重签名阶段，也必须使用CA 给定的代理密钥si，才能生成有效的（Di，Ti，vi）。 因此，任何人要伪造有效的代理多重签名都必须得到有效的si，即得到－ dCA，由于两个大素数pCA，qCA未知且a（n） 是一个未知数，所以其困难度相当于求解ISRSAC 问题。 ISRSAC 算法是在RSA的基础上对加强了大整数n 的分解难度并引入随机性加大了算法计算上的破解难度，其安全性是大于RSA 的。

假设，一个攻击者想伪装成签名者Bi来对消息m 签名，由上面的签名过程中可知，攻击者可以通过随机选择一个数ri′， 计算Ti′≡（ri′）eCAmodmCA和vi′ ＝h（m，Ti′） 来伪造Ti，vi。 但是他不能伪造Di，因为他不能得到si。

假设签名者Bi想签名一个不同消息m′，当Bi ＋1 验证Bi的部分签名时，代入m 来计算vi*，即vi*＝h（m，Ti*）， 从而使得验证不能通过，有效地防止了内部签名者的攻击。

（2）可验证性和可识别性

在这两个方案中，任何人都可通过验证等式hi ＝h（IDBi，mw，ki）或v*＝v是否成立来验证代理多重签名的有效性，且由于在代理密钥和代理多重签名中嵌入了代理签名人的身份标识符，接收者可以有效地验证代理签名人的身份。

（3）不可否认性

由（1）和（2）的分析可知，在这两个方案中，任何人都不能伪造有效的代理多重签名。 同时，收到一个代理多重签名后，任何人都可以验证其有效性，并能够验证代理签名人的身份与原始签名人的授权。 所以，当生成一个有效的代理多重签名后，无论是代理签名人还是原始签名人都无法否认这个签名。

综上所述，这两种代理多重签名方案具有强代理性。

本文的两种签名方案同Teng Yang［5］等人的按序多重签名方案以及广播多重签名方案在安全性上都是基于ISRSAC 算法，Teng Yang［5］等人文章也验证了ISRSAC 算法的安全性是远远优于基于RSA 的。 由此本文设计的签名方案在安全性上是可靠的。 此外本文增加了代理多重的性质，本文设计的方案具有不可伪造性、可验证性、可识别性、不可否认性、强代理性，以上性质使得本文设计的签名方案具有更多功能，可以应用于更加丰富的环境。

7 总结

本文设计了基于ISRSAC 的按序代理多重签名以及广播代理多重签名，并针对其安全性进行分析。 结果表明其在确保安全性的同时满足代理多重签名的性质，本文设计的方案具有不可伪造性、可验证性、可识别性、不可否认性、强代理性。 在两类代理多重签名方案中，一个代理签名人可以同时代表多个原始签名人的利益在一个文件上签名，而签名的方式也可以按照一定顺序或者不分前后顺序来选择。 这使得本文的两种方案在电子商务、网络安全通信、多方公平交换协议、电子选举协议以及移动代理环境方面有较为广泛的应用前景。