关于行列式计算的习题课设计

彭淼 张正娣 沈斌一

1.江苏大学数学科学学院 江苏镇江 212013；2.常熟理工学院 江苏苏州 215506

1 概述

高等代数是大学数学专业必修的一门必修课程。在很多的高校，不仅是数学系的学生，数据计算与应用等相关专业的学生也开设了该课程。由于代数不仅是探讨数学、物理、化学等理论的重要工具，而且在力学、工程、通信中等领域也具有广泛的应用。因此，在高等代数中作为核心部分的线性代数也是大学中理工科专业需要学习的数学工具。高等代数这门课程的特点是概念多、逻辑推理严密、内容量大且较为抽象。通过该课程的学习，可提高学生的抽象思维能力、逻辑思维能力和解题能力，以及为后面的其他课程的学习打下基础。该课程是基础课，因此被安排在大学一年级。由于学生从中学进入大学阶段，思维模式需要经过一个慢慢转变的过程，学习起来比较抽象和吃力，且仅通过课程知识点的讲解在很大程度上不能使学生熟练掌握，因此，习题课是非常重要且必要的。

在行列式计算的课堂教学中，学生可以理解阶行列式的定义以及行列式的7条基本性质。但是，对于课后习题中具体的行列式计算却感觉无从下手，对性质的运用极不熟练，特别是含有字母行列式的题目，不知“何处是归途”。因此，在行列式计算这块内容的习题课上，教师不仅要对基本概念和性质进行总结和回顾，还要对计算方法、步骤进行剖析，帮助学生理清思路，特别是通过一题多解的例子进行讲解，使得学生熟练应用行列式的不同性质，进而提高学生的思考和解题能力。

2 概念与性质回顾

习题课开始时，教师可以利用灵活的教学手段，调动起学生的积极性，让学生回答所理解的级行列式的定义和7条基本性质，并利用简洁易懂的语言总结其抽象的内容，以此来巩固上节课所学的内容。教师能从学生的回答中了解学生哪些知识点还没有理解，哪些数学思想认识还不透彻。

2.1 定义

2.2 性质

(1)行列互换，行列式值不变；(2)行列式某行的公因数可提取出来；(3)若行列式的某行都是两数之和，则行列式可按照此行拆成两个行列式之和；(4)行列式某两行元素对应相等，则值为0；(5)行列式某两行元素对应成比例，则值为0；(6)互换行列式中两行的位置，值反号；(7)行列式某行的倍数对应加到另一行上，其值为0。

需要注意的是，通过性质a知，行列式中行和列地位同等，以上性质对行成立的，对列也成立。

3 行列式习题的讲解

为了使学生更好地理解及运用行列式的定义和性质，掌握好行列式的计算，习题课上应精选典型例题，根据所求的具体行列式的元素特点和规律，采用恰当的解决方法，让复杂的问题变简单。鼓励学生课下多做练习，通过做题不断地总结归纳，积累做题经验。

例1 计算4级行列式

分析：通过行列式的定义知，本题的行列式展开有24项，发现其中非零元素较多，因此只需找出非零项即可。

注：定义法适用于低级(二或三级)行列式和零元素较多的行列式，该方法不太常用。

拓展和推广：用上面例题的解决思路，让学生们思考下面题目，使得学生进一步理解行列式的定义。

设级行列式中有-个以上的元素为0，则该行列式的值为0。

例2 计算5级行列式

分析：通过行列式中元素特点发现，每行都含有1个、4个，每行的元素之和也相等。计算行列式时，性质可以多次交叉使用。

解：将所有列元素加到第一列，再化为上三角行列式。

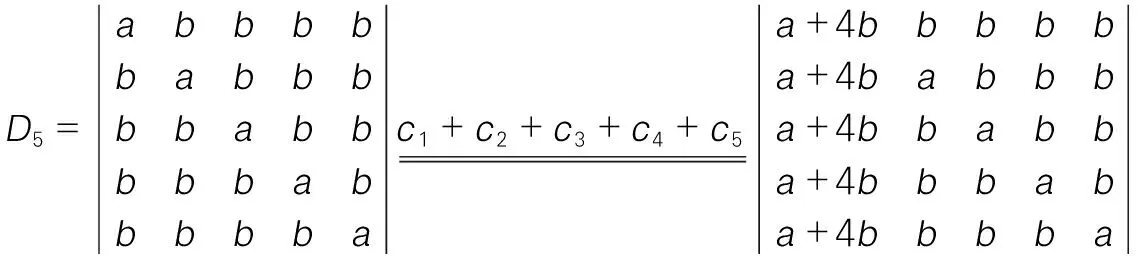
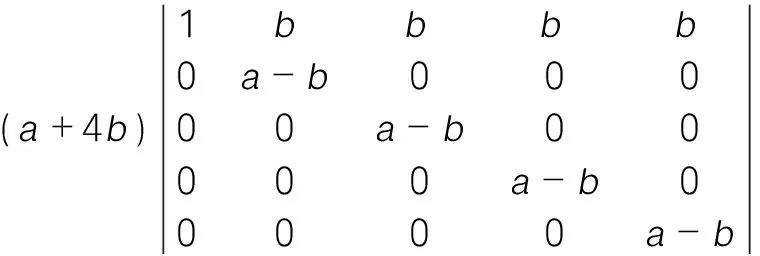
=(+4)(-)

拓展和推广：用上面介绍的解题方法，将5级行列式推广至级行列式，让学生讨论并求解该行列式的值。

例3 计算+1级行列式

其中≠0，=1，2，…，。

分析：通过观察元素特点发现，该行列式除了第一行、第一列及对角元素外其余元素都为0，直观上看像爪子的形状，也被称为“爪字型行列式”。该类行列式通常的方法是将第一行或者第一列消掉。

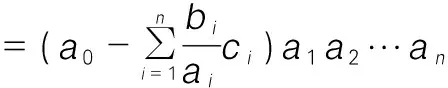
拓展和推广：通过上述行列式的计算，告诉学生们之后再碰到爪字型的行列式该如何求解，有同学会有疑问，实际题目中应该不会直接给出一个爪字型行列式，那该如何运用？能否将给出的行列式进行转化？让学生带着问题再看例2，让学生分组讨论，根据学生的互动，教师来总结是可以转化的。例2的另一解法也可将每一行减去第一行，转化为爪字型行列式，进一步化成三角行列式求解。对于行列式的计算，教师可引导学生尝试采用不同的解法，不仅可加强学生学习的主动性和探索性，也可使学生拓展数学思维。

例4 计算级行列式

分析：观察行列式中元素分布规律，发现元素较多为零，比较直观地发现第1行(列)或者第行(列)，其中都含两个非零元素，故按照降级法来进行解决。

解：首先把按第行展开，得：

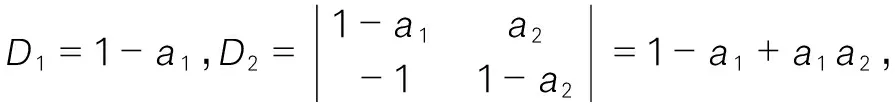
=(-1)…-1+-1=(-1)…-1+((-1)-1…-1+-2)=

=(-1)…-1+(-1)-1…-1+((-1)-2…-2+-3)=…

=(-1)…-1+(-1)-1…-1+…++(-1)

=1-+(-1)+(-1)+…+(-1)…-1

=1---+…+(-1)…-1

上述题目稍微复杂一点，首先利用降级法将行列式变为低级行列式，通过观察发现较低级行列式和原来行列式的形式一样，虽然级数不同，可建立起递推关系，找出，-1和-2之间的关联，利用高中数学学习过的递推关系式的分析，进而算出行列式.我们把这种方法称为降级递推法。

拓展和推广：该行列式的上述处理方法需学生再仔细体会。请学生思考是否还有其他解决方法？提示：学到目前关于行列式的性质c很少用到，引导学生能否借助该性质进行处理。

解法二：先将的第列写成两数之和的形式，将复杂的行列式拆成两个更为简单的行列式。

再来观察拆分得到的第一个行列式比较简单，按照第列展开即可，观察第二个行列式的特点，可依次将每一行元素加至上一行，第行加到-1行，-1行加到-2行，直到第2行加到第1行，简化为下三角行列式。如下：

=-1+(-1)…

得到和解法一同样的递推关系，接下来的推导过程同上述方法一。解法二首先采用一个小技巧，称之为拆边法。通过创建大胆思考的学习氛围，引导学生在之后的计算中，主动使用该方法，进而激发学生的求知欲。

结语

在习题课的实施过程中，教师通过选取经典行列式的例题剖析和讲解，不仅加深学生对定义和性质的理解，而且，教师作为引导者通过课堂讨论等方式来激发学生的积极性，在参与过程中加以启发，及时发现和纠正学生的错误思路，帮助学生理清思路，并且能够对同类型的问题进行不同思路的探究与作答。针对行列式的计算，根据观察行列式中元素特点，选取恰当的解法。犹如在我们的实际生活中，想问题办事情坚持从实际出发，做到实事求是。