基于模糊迭代Q--学习的冶金工业机器人轨迹跟踪控制研究

张 卉，朱永飞，刘雪飞，徐向荣

（1.安徽工业大学机械工程学院，安徽马鞍山 243032；2.安徽工业大学冶金工程学院，安徽马鞍山 243032）

在现代工业中，冶金工业机器人扮演着十分重要的角色。其中，双臂机器人具有良好的协调互助操作优势，弥补了单臂机器人负载较低、可操作性较差以及无法形成闭合机构等缺陷，其目前已成为冶金工业机器人领域的研究热点之一[1-3]。控制技术会影响双臂机器人的系统性能，要提高其位置控制精度，就必须保证控制系统的稳定性。因此，采用稳定的控制方法实现高精度的运动控制具有非常重要的意义[4-5]。

传统的控制方法主要有基于精确数学模型的PID（proportional integral derivative，比例积分微分）控制。但是，多自由度双臂机器人是一种多输入、多输出且具有强耦合作用的复杂系统，具有非线性、时变不确定等特点[6-7]，难以建立精确的数学模型。为实现双臂机器人高精度的轨迹跟踪控制效果，朱永飞等[8]基 于 ADAMS（automatic dynamic analysis of mechanical systems，机械系统动力学自动分析）和MATLAB软件对6-DOF（six degree-of-freedom，六自由度）双臂机器人进行了联合仿真，采用B样条曲线插值方法完成了其轨迹规划任务，但该研究仅从运动轨迹规划方面展开，缺乏对机械臂控制器的设计和搭建。刘雪飞等[9]实现了机械臂末端执行器在避障条件下的高精度位置跟踪，解决了非结构环境下机械臂的安全运动轨迹规划问题。然而，上述学者仅从运动学角度对双臂机器人的轨迹跟踪进行了研究，为进一步提高机器人轨迹跟踪的控制精度，不少学者从控制算法角度出发展开相关研究。对于数学模型不精确的复杂系统，在其控制策略中引入模糊控制[10-11]，即利用模糊控制对动力学模型中未知部分和扰动部分的非线性逼近特性，取得了良好的控制效果。例如：李德昀等[12]将自适应模糊控制策略应用于双臂机器人的协同搬运作业，实现了平稳的力矩输出控制及精准的接触力控制，具有较强的鲁棒性和自适应性。另外，现阶段的机器人大多是按设定好的程序进行大量重复性操作，比如搬运物体、激光切割和定点抓取等，在外界环境干扰和本体磨损等因素的影响下，机器人的重复性操作准确性势必会下降[13-15]。而迭代学习控制方法[16-17]非常适用于做重复性操作任务的机器人控制系统，且该控制方法所需的控制对象数学模型可以是不准确的，其是一种易于实现、鲁棒性强、轨迹跟踪效果较好的智能控制方法。

鉴于机器人的动力学模型受各种复杂外界干扰的影响，为了更好地补偿其动力学模型中未知部分和外界扰动所产生的影响，以及提高其轨迹跟踪精度，笔者提出了一种基于模糊迭代Q-学习的控制算法，即将模糊迭代控制方法与Q-学习方法相结合。其中：模糊控制的万向逼近特性可对动力学模型中的未知惯性参数进行估计，而模糊控制的调节因子可由Q-学习控制器得到。最后，将所提出的控制算法应用于6-DOF双臂机器人，并联合ADAMS和MATLAB软件开展机器人轴孔装配仿真实验。

1 模糊Q-学习控制器

1.1 模糊控制器介绍

模糊控制器包括模糊化、知识库（含数据库和规则库）、模糊推理和清晰化等4个部分[18-19]，其结构框图如图1所示。

图1 模糊控制器结构框图Fig.1 Structure block diagram of fuzzy controller

在整个模糊控制系统中，模糊控制器是最核心的部分，其最主要的任务是通过编写模糊规则和近似推理来得到最终的输出结果。这一过程本质上就是对模糊集合进行数学计算的过程，起始输入量x到最后输出量u在模糊控制器中会经历先从清晰到模糊，再从模糊到清晰的双向变化过程，以便得到更加符合实际需要的控制效果。

1.2 模糊Q-学习控制器结构设计

在大多数情况下，经过模糊处理的输出结果U可表示为：

式中：e、分别表示控制系统的误差和误差变化率；β表示模糊控制的调节因子，当系统误差较大时，可提高模糊规则中的误差权重，以有效地控制误差范围，当系统误差较小时，系统正趋向稳定状态，可提高模糊规则中误差变化率的权重。

Q-学习算法是一种新颖的无模型强化学习方法，可以和模糊控制方法相结合，用于获取模糊控制中的调节因子β。将误差e作为Q-学习算法输入的状态空间集合，根据e的变化来调整调节因子β的大小，实现对模糊规则的进一步优化。

模糊Q-学习控制器的结构如图2所示。图中：yd表示输入值，y表示输出值，KP、KD分别表示误差和误差变化率的增益矩阵，KU为比例因子。由于模糊控制器受到2个输入变量的影响，图2所示为二维模糊控制器，其是目前模糊控制系统中应用最多的一类模糊控制器。

图2 模糊Q-学习控制器结构Fig.2 Structure of fuzzy Q-learning controller

在本文所设计的模糊Q-学习控制器中，奖励函数R取：

式中：e＊表示e的目标值，在本文中取0。

式（2）所示的奖励函数满足：当e偏离0越大时，得到的奖励越小；当e偏离0越小时，得到的奖励越大。

2 模糊迭代Q--学习控制器设计

2.1 迭代学习控制基本原理

通常情况下，机械臂的轨迹跟踪误差ek(t)可以表示为：

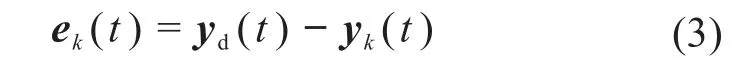
式中：k表示迭代次数。

为实现机械臂的高精度轨迹跟踪，引入闭环迭代学习控制算法，使得误差ek(t)不断减小。

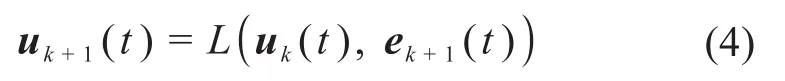
式中：L表示非线性算子；uk(t)、uk+1(t)表示第k、k+1次迭代的输入变量。

则PD迭代学习控制律可表示为：

在整个控制系统的运行过程中，增益矩阵KP和KD保持不变，即不能根据系统状态的变化自适应地调整矩阵中各元素的值，故需要通过对控制律中的增益矩阵进行实时调整来获取最优参数。采用模糊控制器和迭代学习相结合的方式，完成对PD控制参数的调整选取，以改善整个控制系统的动态性能。

2.2 模糊迭代Q--学习控制器结构设计

基于上述原理，设计模糊迭代Q-学习控制器，其结构如图3所示。将基于迭代学习控制产生的误差ek以及误差变化率作为模糊控制器的输入变量，经模糊化、近似推理和清晰化处理后输出的变量是修正后的PD补偿参数ΔKP和ΔKD，将其与经验PD控制参数相加后得到最终的最优KP和KD，从而实现机械臂关节角度的跟踪误差最小化。

图3 模糊迭代Q-学习控制器结构Fig.3 Structure of fuzzy iterative Q-learning controller

根据图3，模糊迭代Q-学习控制器可表示为：

式中：KPI、KDI表示经验PD控制参数。

2.3 模糊迭代Q--学习控制器收敛性验证

3 双臂机器人的联合仿真实验

3.1 基于ADAMS和MATLAB的联合仿真平台搭建

为了验证本文所提出的模糊迭代Q-学习控制算法的有效性与优越性，在ADAMS和MATLAB软件中进行联合仿真实验。以6-DOF双臂机器人为研究对象，先在SolidWorks软件中绘制其三维模型。该机器人的左右机械臂各有6个自由度，且左右机械臂构型对称。采用改进的D-H法建立连杆坐标系（以左机械臂为例），从基座到末端执行器的关节分别定义为1～6，具体参数如表1所示。其中：θi、αi-1、di、ai-1分别表示关节转角、连杆扭角、连杆偏距和连杆杆长。

表1 左机械臂的D-H参数Table 1 D-H parameters of left mechanical arm

然后，将构建好的6-DOF双臂机器人三维模型文件另保存为Parasolid格式，然后导入ADAMS软件以构建其仿真模型，如图4所示。

图4 6-DOF双臂机器人仿真模型Fig.4 Simulation model of 6-DOF dual-arm robot

在ADAMS软件中对6-DOF双臂机器人仿真模型进行设置，并通过信息选项获取机器人每个零部件的质心坐标及惯性参数。以左机械臂为例，其各个关节的动力学参数如表2所示。

表2 左机械臂的动力学参数Table 2 Dynamic parameters of left mechanical arm

接着，点击ADAMS软件中的单元建立状态变量，对6-DOF双臂机器人左右机械臂的状态变量进行设置，依次为各关节的角度、角速度以及力矩。

最后，利用ADAMS软件中的controls插件对机械臂控制系统的输入、输出进行设置：输入变量为力矩，输出变量为角度和角速度；目标软件设为MATLAB；ADAMS solver选项为非线性，求解器设为FORTRAN。

图5所示为机械臂控制子系统模块，需要对ADAMS_sub中的ADAMS Plant模块进行Simulink和ADAMS同步仿真参数设置，如图6所示，并在Interprocess option选项中选择 PIPE（DDE），在Animation mode中选择interactive。完成设定后，可在运行Simulink时使ADAMS同步仿真。

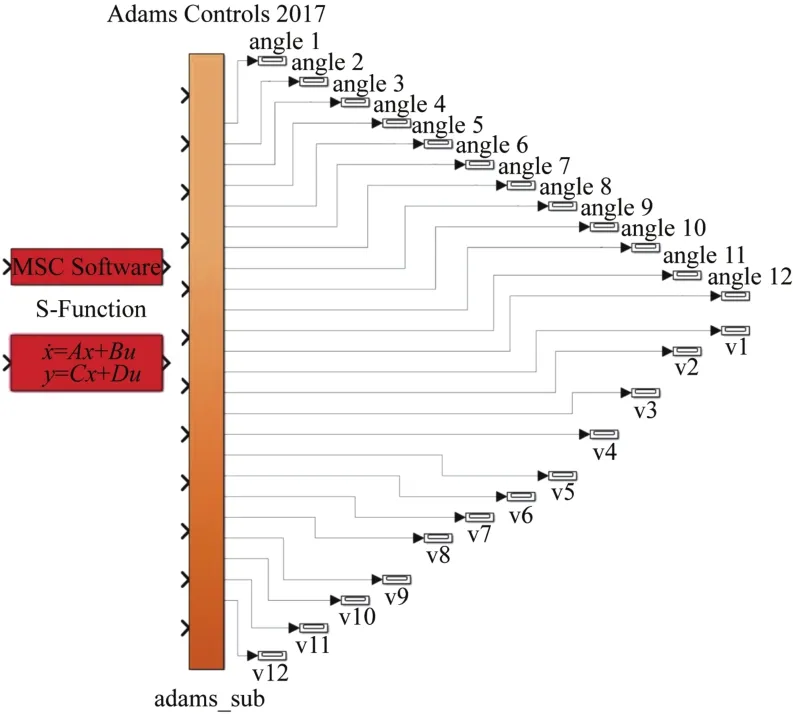
图5 机械臂控制子系统模块Fig.5 Mechanical arm control subsystem module

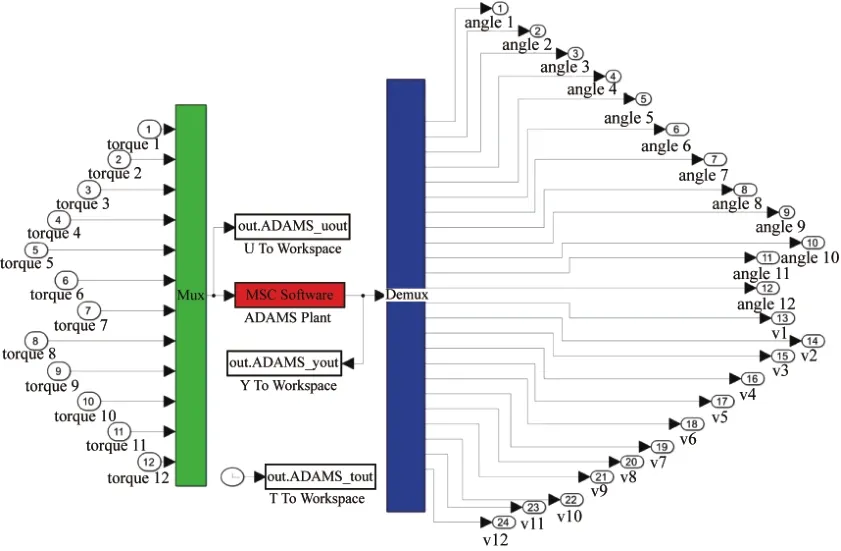
图6 机械臂控制子系统模块输入和输出变量设置Fig.6 Input and output variable setting of mechanical arm control subsystem module

3.2 双臂机器人轨迹跟踪控制仿真实验

设置6-DOF双臂机器人轨迹跟踪控制仿真总时长为3 s，迭代次数为20。以左机械臂为例，设期望轨迹为正弦曲线，其6个关节的轨迹跟踪结果如图7所示。由图可以看到，各个关节的实际轨迹跟踪效果较好，跟踪精度较高，验证了所提出模糊迭代Q-学习控制算法的有效性和优越性。

图7 左机械臂各关节的轨迹跟踪结果Fig.7 Trajectory tracking results of each joint of left mechanical arm

3.3 双臂机器人轴孔装配仿真实验

在控制6-DOF双臂机器人进行轴孔装配之前，假定其左右机械臂的末端执行器已经分别夹持了轴和孔，故只需考虑双臂末端的轴孔装配路径。鉴于在轴孔装配实验中左右机械臂作对称运动，仅分析单机械臂的关节运动即可。图8所示为6-DOF双臂机器人的轴孔装配过程。

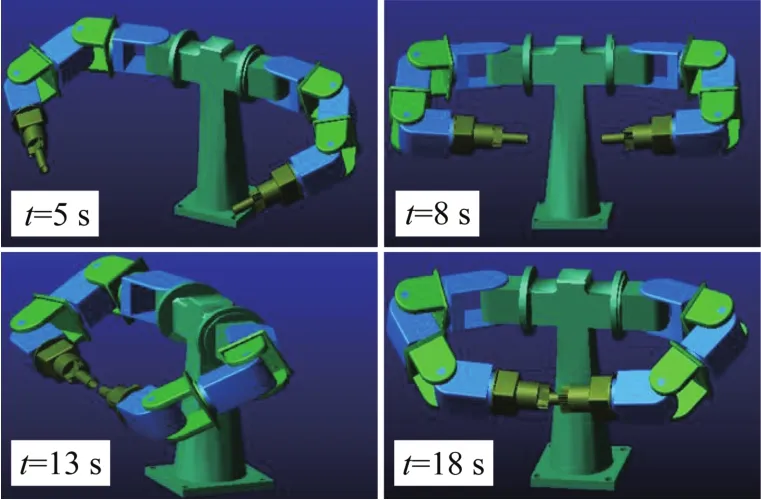
图8 6-DOF双臂机器人的轴孔装配过程Fig.8 Shaft hole assembly process of 6-DOF dual-arm robot

由图8可知，6-DOF双臂机器人的轴孔装配成功，验证了所提出控制算法的正确性。利用MATLAB软件的仿真数据以及与ADAMS软件联合仿真得到的数据，对左机械臂各关节的角度和角速度等进行分析，结果如图9所示。

图9 轴孔装配过程中左机械臂各关节的动力学特性Fig.9 Dynamic characteristics of each joint of left mechanical arm during shaft hole assembly

观察图9（a）和图9（c）可知，左机械臂各关节的角度变化平缓且无突然波动的情况，关节角度的最大误差约为0.004 rad，关节角速度的最大误差约为0.001 5 rad/s。此外，由于轴孔装配过程分为2个阶段，2个阶段之间稍有停顿，故在t=8 s附近，关节角度和角速度出现了短暂为零的情况。图9（e）所示的左机械臂输入力矩变化曲线整体较为平滑，未出现力矩抖振现象，说明该机械臂的整体运动效果较好，进一步验证了所提出的模糊迭代Q-学习控制算法的有效性和稳定性。

4 结 论

1）针对冶金工业机器人控制不稳定、轨迹跟踪精度较低和自适应性较差的问题，提出了一种模糊迭代Q-学习控制算法。

2）联合ADAMS和MATLAB软件搭建6-DOF双臂机器人仿真模型，并以正弦曲线作为期望轨迹进行轨迹跟踪仿真分析。结果表明，该机器人各关节的轨迹跟踪效果较好，实现了关节空间内的低误差轨迹跟踪。

3）6-DOF双臂机器人的轴孔装配仿真结果表明，各关节角度的误差不超过0.004 rad，角速度误差不超过0.001 5 rad/s，且各关节的角度变化曲线和输入力矩变化曲线平稳光滑，无剧烈抖振和突变现象，验证了所提出模糊迭代Q-学习控制算法在冶金工业机器人轨迹跟踪控制中的有效性和优越性。